一道高考导数压轴题的解法探究

广东省中山市濠头中学 (528437) 李 方 杨沛娟

一、试题呈现及分析

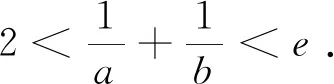
分析：(1) 首先确定函数的定义域，然后求得导函数的解析式，求出函数的导数，由导函数的符号即可确定原函数的单调性.

二、试题解答

第(1)小题解法如下：f(x)的定义域为(0,+∞)．由f(x)=x(1-lnx)得f′(x)=-lnx，当x=1时，f′(x)=0；当x∈(0,1)时f′(x)>0；当x∈(1,+∞)时，f′(x)<0．故f(x)在区间(0,1]内为增函数，在区间[1,+∞)内为减函数.

本文主要分析第(2)小题的解法.

先证x1+x2>2.若x2≥2，x1+x2>2必成立.若x2<2， 要证x1+x2>2，即证x1>2-x2，而0<2-x2<1，故即证f(x1)>f(2-x2)，即证f(x2)>f(2-x2)，其中10，所以g′(x)>0，故g(x)在(1,2)为增函数，所以g(x)>g(1)=0，故f(x)>f(2-x)，即f(x2)>f(2-x2)成立，所以x1+x2>2成立.综上，x1+x2>2成立.

设x2=tx1，则t>1，结合

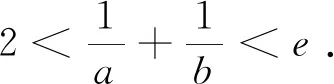
评注：极值点偏移问题，一般利用通过原函数的单调性，把与自变量有关的不等式问题转化与原函数的函数值有关的不等式问题，也可以引入第三个变量，把不等式的问题转化为与新引入变量有关的不等式问题.

[2]雍照章.开发中职专业技能课程标准的基本问题分析 [J].职业技术教育,2017,38(10):24-29.

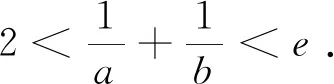
评注：等价转化是处理导数问题的常见方法，其中利用的对称差函数，构造函数的思想，这些都是导数问题必备的知识和技能.

令f(x)=x(1-lnx)，则f(m)=f(n)，不妨设m2．要证m+n>2⟺n>2-m⟺f(n)2．

再证m+nm，所以需证n(1-lnn)+n0，故h(x)在(1,e)内单调递增．所以h(x)

评注：等价转化是常见的数学思想，构造对称差函数是最基本的极值点偏移问题的处理策略.

点评：解法4用到了比值代换，这是一种将双变量问题化为单变量问题的有效途径，然后构造函数利用函数的单调性证明题中的不等式即可.

评注：解法5用到的是构造函数法，构造函数之后想办法出现关于x1+x2-e<0的式子，这是本方法证明不等式的关键思想所在.