HPM视角下“等比数列的前n项和公式”的教学*

宜宾学院人工智能与大数据学院 (644000) 覃 淋

巴中职业技术学院教育学院 (636000) 喻晓婷

1 引 言

《普通高中数学课程标准(2017)》在“教材编写建议”中指出，“要体现数学内容的逻辑体系，揭示数学内容的发生、发展过程……创设合适的问题情境，设计有效的数学学习活动，展示数学概念、结论、应用的形成发展过程．”数学史作为数学教学的重要资源，数学史的教育价值也得到了理论与实践两个层面的普遍认同．美国数学史家卡约里(FlorianCajori，1859-1930)认为“数学史是使面包和黄油更加可口的蜂蜜”，在其著作《AHistoryofMathematics》(1926)中指出：“如果用历史轶事点缀枯燥的计算和证明，学生的兴趣就会大大增加．…… 通过对数学历史的介绍，能够让学生明白数学并不是一门呆板乏味的学科，而是一门不断进步且生动有趣的学科.”有学者从概念、文化、动机三个层面讨论了数学史的教育价值，指出数学史具有帮助学生拓宽视野、增加兴趣、创造学习动机、促进学生思考等教育价值．数学史融入课堂教学的实践表明，数学史具有知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效等多元的教育价值和文化价值．

“等比数列的前n项和”是人教A版高中数学选择性必修二第4章《数列》4.3节的内容，是“等差数列”内容的延续，是进一步学习数列知识和解决一类求和问题的重要基础和有力工具．等比数列模型在实际生活中有着广泛的应用，蕴含了一些重要的数学思想方法．《普通高中数学课程标准(2017)》中要求学生“探索并掌握等比数列的前n项和公式，理解等比数列的通项公式与前n项和公式的关系．”

本文通过选取历史上的素材，设计一系列问题，将数学史上不同地区、不同民族关于等比数列求和公式的多种推导方法融入课堂教学，让学生了解数学知识的发生发展的历程，感受数学的文化多元性，领略数学文化的魅力，形成动态的数学观，发展学生的数学核心素养；并通过数学史融入课堂教学，培养学生对数学积极的情感态度，营造人性化的课堂，在潜移默化中实施数学学科德育，落实立德树人根本任务．

2 教学设计与实施

2.1 创设情境，呈现问题

首先引导学生复习前面学习的等差数列的定义、通项公式、前n项和公式及等比数列的通项公式等内容．然后提出19世纪初，美国数学家亚当斯(D.Adams，1773-1864)的著作《学者算术》中的妻子问题：我赴圣地伊夫斯，路遇一男携七妻，一妻各自负七袋，每袋都装七猫咪，猫咪又把七仔生，同去圣地共几何？

对于这个问题，学生很容易想到把每项算出来，再相加．接着教师再用PPT呈现“棋盘问题”，教师再向学生提问，“如何计算棋盘上的麦粒总数？”

在学生交流讨论的同时，教师播放制作的微视频介绍等比数列求和问题的历史以及历史上一些著名的等比数列求和问题．

2.2 合作交流，探究规律

教师通过课前制作的微视频，介绍等比数列求和公式推导的可能思路．引导学生分小组进行探究．小组讨论后，请各组代表分别上台展示．

小组一：(错位相减法)利用错位相减法推导公式，学生的思路如下：

小组二：(古埃及的方法)由等比数列的定义，找到前n项与前n-1项的关系，得到二者的等量关系，学生思路如下：

小组六：(几何推导法之一)假设等比数列首项a1>0，公比为q>0，学生的推导思路如下：

如图1，在一个正切值为公比q的直角三角形中，在底边作出长度为a1的线段，再作垂线段交于斜边，那么垂线段的长度为a2=a1q；再从交点出发，作长度为a2的与底边平行的线段，然后再向上作垂线交于斜边，则垂线段的长度为a3=a2q；以此类推，直到第n-1步，作长度为an-1的与底边平行的线段，然后再向上作垂线交于斜边，则垂线段的长度为an=an-1q．底边的长度为a1+a2+…+an-2+an-1，另一直角边的长度为a2+a3+…+an-1+an．从而有q=

图1

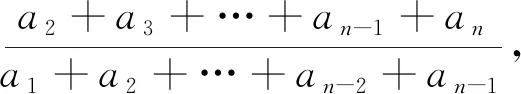
图2

2.3 教师总结规律

2.4 应用规律

随后，教师要求学生利用求和公式解决一些问题，体会数学的实用性．

问题1 某国王征兵，规定第一个村子征兵1人，第二个村子征兵2人，第三个村子征兵4人，第四个村子征兵8人，以此类推，直到第三十个村子，问：一共征兵多少人？(阿尔昆《敏锐青年之命题》)

问题2 今有出门，望见九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色．问共几何？(《孙子算经》)

问题3 远望巍巍塔七层，红灯点点倍加增．共灯三百八十一，请问尖头灯几盏？(《算法统宗》)

2.5 总结提升

本节课学习了等比数列的前n项和公式，从古巴比伦泥版上的分财产问题，经历了古埃及人、《几何原本》、印度数学家、中世纪欧洲数学家，再到欧拉《代数学基础》中的错位相减法，领略了历史上等比数列求和公式的不同精彩证法．同学们在本节课中学习了多种数学思想方法：特殊到一般的思想、方程的思想、数学结合的思想、分类讨论的思想，同时也培养同学们的数学抽象、数学运算、直观想象、逻辑推理以及数学建模等数学核心素养．并且通过对不同文明中等比数列求和公式的不同推导方法的介绍，让我们多了一个观察角度，多了一种表达方式，多了一种研究手段．

3 学生反馈

课后，对全班41名学生进行问卷调查．80%的学生听懂了本节课的内容，极少部分基础较差的学生觉得本节课课堂容量有些大．95%的学生喜欢本节课中数学史融入课堂的教学方式，希望老师在以后的教学中也多采用这样的方式进行教学．

学完本节课后，学生会想到的关键词有：巴比伦泥版、纸草书、《孙子算经》、《几何原本》、《算法统宗》、欧拉、数学文化、数学史等．

关于本节课中印象最深的内容，学生的典型回答有：古埃及人的计算方法非常巧妙，但我们也不能完全局限于他们的思路；历史让人穿越迷雾，感受到了数学的脉动；解决同一问题常常有不同的方法，让人大开眼界；历史上的数学问题很有意思，很多公式的发明创造，都是数学家为了解决实际问题的而创造的；数学公式并不是凭空产生的；数学文化博大精深，中国古代数学家在数学上也做出了很大贡献．

学生的这些回答，正如法国数学教育家J.Swetz所言：“在数学问题求解中可选取历史上不同时期、不同文化的一些数学名题．这些名题及其解答提供了实质性的数学思想方法，并蕴含了数学家为之奋斗的曲折历程与苦乐体验，展现了生动而广阔的人文背景．”

关于本节课中等比数列的前n项和问题的历史印象对数学学习的帮助和启示，学生的典型回答有：今天一节课的内容是古人几千年智慧的结晶；数学史、历史数学名题既可以增加课堂的趣味性，又可以帮助记忆、理解公式；学习数学家不畏艰险、刻苦专研的精神；课堂上应该多介绍一些关于数学知识的历史，扩充背景有利于数学学习；数学史让数学变得有意思；同一个问题，从不同的思路出发，都可以解决问题．

课后访谈表明，学生对于第一次在数学课堂中深入接触数学史，感觉比较新鲜，知道了等比数列求和问题古已有之，通过对数学发展史的了解，感受到了数学史对自己数学学习的帮助，并且认为数学史的融入活跃了课堂气氛，增加了课堂的趣味性，也激发了学习兴趣．同时也认识到数学与不同的学科之间都有着密切的联系．在课堂教学中，数学史为学生提供了许多探究的机会，让学生可以在教师的引导下经历“火热的思考”，变为“数学家”，把数学“再创造”出来．学生在这样的学习过程中，既拓宽了视野，又体会了“再创造”数学的喜悦．

4 结 语

等比数列的前n项和公式是高中数学的重要内容，教材中介绍的“错位相减法”具有较强的技巧性，如无教师引导，学生很难想到．对学生而言，这样的知识是不“自然”的．我们基于HPM的视角，设计课堂教学，从学生已有知识结构出发，创设问题情境，引起认知冲突，搭设“脚手架”，使得公式的产生变得自然，揭示了数学知识之谐；通过古今方法的比较，呈现了数学方法之美；将历史与现实相联系，同时为学生提供了探究的机会，让学生体验了探究之乐；以故事的形式让学生用所学知识解决问题，培养了学生解决问题的能力，达成了能力之助．通过对不同文明中等比数列求和问题的介绍，凸显人文元素，将历史与现实、数学与人文、数学与科学联系起来，通过历史把数学的“学术形态”转化为“教育形态”，降低了学生数学学习的外在认知负荷．既培养了学生的多元文化视角，又渗透了数学文化，展示了数学文化的魅力．通过等比数列求和公式不同时期的不同推导方法的介绍，让学生明白数学是不同时期数学家共同努力的智慧成果，培养学生独立思考、敢于质疑、追求创新的理性精神，达成了德育之效．