软岩隧道锚固系统预紧力匹配性设计方法与实践
2023-03-29郭新新汪波刘锦超王振宇
郭新新 ,汪波,刘锦超,王振宇
(1. 成都理工大学 环境与土木工程学院,四川 成都 610059;2. 西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031)
随着以川藏铁路为代表的一批埋深千米级甚至数千米级的长大深埋地下工程大量出现,隧道工程呈现出应力场赋存状态高、软岩分布范围广等显著特点,由此带来的高地应力软岩隧道大变形灾害问题极为突出[1-2],给现行依赖围岩变形而施载的“全被动”强力支护模式带来了巨大的挑战[3]。针对被动支护模式几无调动围岩自承载能力的缺陷,目前部分学者创新地提出了以预应力锚固系统为核心的软岩隧道变形主动控制方法[4-5]。在断面开挖完成后,采用预应力锚固系统快速地对开挖轮廓施加主动支护力,进而构建起以围岩自承载为核心的支护体系,截至目前,变形主动控制方法已在G75 高速木寨岭公路隧道中取得了极大成功,实现了初期支护体系拆换率由初始30%到0 的突破性转变[6]。上述软岩隧道变形主动控制的核心在于预应力锚固系统,故科学合理设计预应力锚固系统的参数将是关键所在。其中的预紧力,即锚固系统(锚杆/索)施加预应力时,通过拧紧螺母或采用张拉方法施加在锚杆、锚索上的拉力,作为变形主动控制中最核心的参数,更是一个涉及力学、技术和经济在内的综合参数[7]。目前针对锚固系统预紧力的设计主要有基于锚杆/索材料性能或锚固界面力学性能的方法,如罗基伟等[8-9]提出锚固系统预紧力宜设计为锚杆/索材料拉断载荷的40%~70%,CHANG 等[10]提出了通过开展不同锚固长度锚杆现场拉拔试验进行预紧力确定的方法;以及基于变形控制效果的方法,如李志臣等[11]提出了以巷道顶板变形作为主控指标的锚杆/索预紧力设计方法,张建海等[12]提出了基于围岩时效变形特征的锚索预紧力设置方法,王洪涛等[13]提出了基于顶板冒落破坏上限分析的预紧力简化设计方法。但实际上,从加载过程中锚固系统与围岩相互作用角度出发,预紧力最先是由围岩、锚固剂和锚杆/索体三者共同管控,安全、合理的预紧力设计/选用首先应是建立在对锚固系统锚固性能的研究基础之上[14]。而针对锚固性能的研究,在围岩、锚固剂和锚杆/索体材料确定前提下,关键在于对锚固长度的合理确定[15]。因此,预紧力的设计/选用,本质上即可归结为是在确定锚杆/索材料基础上,所开展的预紧力与锚固长度的匹配性设计。综上,本文将首先对软岩隧道锚固系统锚固力(性能)与锚固长度的关系开展研究;其后,综合安全、经济及施工等多种因素,提出适用于软岩隧道预应力锚固系统预紧力的匹配性设计方法;最后,依托木寨岭公路隧道开展工程应用实践,获取适用于木寨岭公路隧道不同预紧力下的锚固系统设计参数。
1 软岩隧道锚固系统锚固力与锚固长度关系
1.1 锚固力的理论解析
交通隧道工程中的预应力锚固系统属永久支护形式,一般要求锚固界面应力处于弹性阶段、避免出现塑性,为此定义锚固力(最大承载力)为锚固界面处于弹性受力阶段时,锚固系统能达到的最大抗拔力。同时,鉴于软岩隧道具有围岩强度低、钻孔黏结性能弱、成孔效果差及多数钻孔潮湿(淋水)等特性,锚固剂与围岩间的界面一般是锚固系统中最薄弱的环节,锚固强度(破坏)也大多取决于该界面的抗剪强度[16-17],因此,理论分析中设定如下假设:
1) 锚固系统的最终失效形式为锚固剂-围岩界面滑移;
2) 锚固界面弹性变形时,视锚杆/索体与锚固剂为一体,受力变形过程中不计参数的变化,如此,确定复合弹性模量Ea计算如下,
式中:Em,Es分别为锚固剂与锚杆/索体的弹性模量,Pa;D,d分别为钻孔直径、锚杆/索体的直径,mm。
图1(a)为预应力加载状态(拉拔状态)下锚固系统锚固段的受力分布。以锚固起始点为起点,设定指向围岩深处为x轴正方向,取长度dx的微元体分析,如图1(b)所示,根据物理方程和平衡方程,得到dP(x),

图1 预应力加载状态下锚杆/索受力示意图Fig. 1 Schematic diagram of bolt/cable stress under prestressed loading
式中:P(x)为x处复合体的轴力;τ(x)为x处锚固剂与围岩界面的剪应力,根据三阶段线性函数表示的界面弹性状态荷载传递关系[18],并设锚固剂与围岩界面的(弹性)剪切刚度系数为Ke,则τ(x)计算如下,
式中:u(x)为x处复合体的轴向位移。结合式(2)和式(3)得到,
当τ(0)=[τ]时,P0达到最大值,即为锚固力Pe,
式中:[τ]为锚固剂与围岩界面的抗剪强度。
1.2 锚固力与锚固长度关系
分析式(7),βL=3,tanh(βL)>0.99≈1,此时,Pe已基本达到最大值,即极限锚固力,记作Pue,对应的锚固长度为临界锚固长度,记作Lc,分别计算如下,
根据式(7)~(9),绘制不同锚固长度下的锚固力变化如图2 所示,其中横坐标为L/Lc,纵坐标为Pe/Pue。

图2 不同锚固长度下的锚固力变化Fig. 2 Variation of anchoring force under different anchoring lengths
图2 所示,临界锚固长度内,随锚固长度增加,锚固力增大,但增速快速趋缓。当L/Lc=0.5,Pe/Pue=0.9,显示当L/Lc>0.5 后,锚固长度即使增加一倍,锚固力增幅不超过10%。故从锚固力提升效率角度考虑,锚固长度实则无超0.5Lc的必要。
2 多因素综合下锚固系统预紧力匹配性设计方法
2.1 设计基本原则
1) 锚杆/索体型号与预紧力相匹配:定义锚杆/索材料性能发挥率β(=预紧力/最大设计承载力Nt),要求0.85≤β<1。
2) 锚固可靠性:预紧力达到最大设计承载力Nt时,锚固始端最大剪应力为[τ]/α1,其中α1为安全储备系数,大于1;预应力加载过程,锚固始端最大剪应力始终小于抗剪强度[τ]。
3) 锚固力提升效率:设计锚固长度应<0.5Lc。
4) 施工锚固效果:设计锚固长度时需考虑具体施工工艺,应保证施工锚固效果稳定、可靠。
2.2 设计基本流程
图3为多因素综合下的预应力锚固系统预紧力匹配性设计流程:1) 通过在典型软质岩体、且围岩变形较大段落开展不同锚固长度现场锚固系统拉拔试验,获取关键性设计参数抗剪强度[τ]和剪切刚度系数Ke;2) 根据理论计算公式,计算得到极限锚固力Fue和临界锚固长度Lc;3) 划分预紧力设计区间,计算不同锚固构件的性能发挥率,确定与之匹配的锚杆/索型号;4) 计算考虑预应力加载损失的锚固长度下限Lmin1,要求此时最大剪应力τ小于抗剪强度[τ];计算考虑安全储备系数α1的最小锚固长度下限Lmin2,要求此时最大剪应力τ小于抗剪强度[τ]/α1;综合确定锚固长度下限Lmin(=max[Lmin1,Lmin2]);5)计算考虑锚固力提升效率的锚固长度上限Lmax1(=0.5Lc);考虑施工锚固效果的稳定性、可靠性,结合现场施工实际、并参照类似工程经验,得到(适宜)锚固长度上限Lmax2;综合确定锚固长度上限Lmax(=min[Lmax1,Lmax2]);6)综上,获取不同预紧力设计工况下的锚杆/索型号以及适宜锚固长度区间,即谓之软岩隧道锚固系统的预紧力匹配性设计。
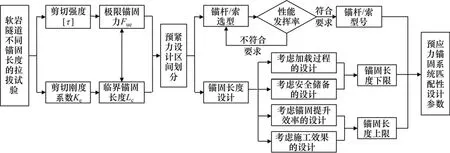
图3 预应力锚固系统预紧力匹配性设计流程Fig. 3 Design flow of prestress matching of prestressed anchorage system
3 工程应用-木寨岭公路隧道预紧力匹配性设计
3.1 试验方案
1) 围岩条件
在建渭武高速木寨岭公路隧道位于甘肃中部定西市境内,全长15.226 km,埋深最大629.1 m,实测最大地应力18.76 MPa,与兰渝铁路木寨岭隧道水平距离约900~1 200 m,单洞开挖断面面积>120 m2。地勘显示隧道穿越岩性以软质炭质板岩为主,多呈黑灰色、薄层状,物理力学参数取值如表1所示。

表1 炭质板岩物理力学参数Table 1 Mechanical parameters of carbonaceous slate
拉拔试验在木寨岭公路隧道里程YK218+030~+020上、中台阶开展,该区段拱顶下沉120~210 mm、拱腰收敛400~520 mm,围岩岩性主要为薄层状炭质板岩(夹砂质板岩),层厚1~20 cm,如图4(a)所示,3组岩块点荷载试验(图4(b))换算单轴抗压强度23.3,25.1 和33.4 MPa,平均强度27.3 MPa,归属软岩范畴。

图4 典型掌子面围岩及点荷载试验Fig. 4 Typical tunnel face surrounding rock and point load test
2) 试验材料
试验采用1×19 s-21.80 mm-1 860 MPa 鸟笼型锚索,最大力>583 kN,屈服力(0.2%)>513 kN,伸长率>3.5%;鸟笼段长度1.2 m,含4节“鸟笼”膨胀节(图5(a)),最大直径34 mm。试验用锚固剂为CKb3540 树脂锚固剂(金旭德)(图5(b)),符合《MT146.1-2011 树脂锚杆+第1 部分:锚固剂》要求。

图5 试验材料Fig. 5 Test materials
3) 试验工况与过程
依据研究目的,试验拟定了不同锚索长度、不同锚固长度,共3 组试验(每组3 根锚索),具体试验信息如表2所示。
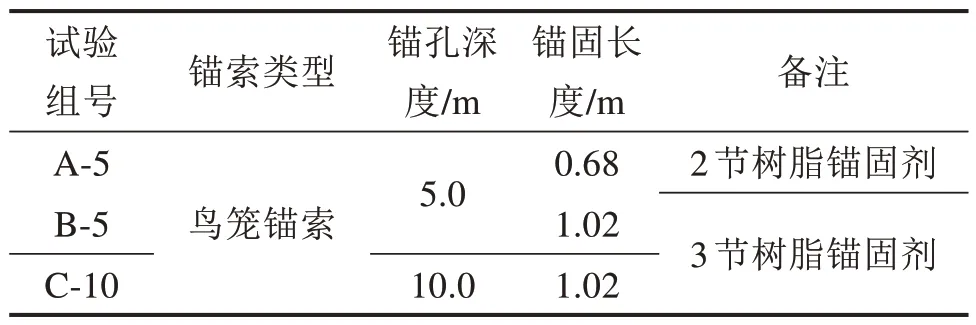
表2 锚索拉拔试验工况Table 2 Conditions of anchor cable drawing test
试验过程如下:① 采用“气动锚杆钻机+小、大组合PDC 钻”(图6(a))打设Φ47 mm 锚孔;② 采用ZQS-50/2.3S 型气动手持式钻机(图6(b))搅拌锚固;③ 锚固15 min 后,采用MQ22-450/60 手动油压穿心千斤顶(图6(c))进行拉拔。试验过程中每加载25 kN,记录1 次端部位移数据。参照《GB/T 35056—2018 煤矿巷道锚杆支护技术规范》,设定锚固失效准则为当加压至某一级荷载后,进一步加压时,锚杆端部位移不断增长,而压力表值难以增至下一级荷载甚至出现下降。

图6 试验设备与现场位移量测Fig. 6 Test equipment and field displacement measurement
3.2 试验结果与数据
为探究鸟笼树脂锚索在木寨岭公路隧道中的实际破坏形式,将A-5 组中1 根锚索完全拉出,如图7 所示,显示破坏形式(主要)为锚固剂-围岩界面滑移,与理论分析中的假设相符。

图7 锚固剂-围岩界面破坏实例Fig. 7 Failure example of anchoring agent surrounding rock interface
获取不同锚固长度下锚索的荷载-位移(P-S)曲线如图8 所示。图中数据为每组3 根锚索的平均值。

图8 不同锚固长度下锚杆的荷载-位移曲线Fig. 8 Load-displacement curve of anchor rod with different anchorage length
由图8可以看出:
1) 树脂鸟笼锚索的拉拔过程的P-S曲线基本一致,主要包含4个阶段,以A-5试验组为例:① 初始压密阶段(oa):P-S曲线斜率逐渐增大,此时的位移主要来自于锚固界面的弹性变形、垫板与围岩面的压缩位移、鸟笼锚索的拉伸;② 中期弹性阶段(ab):P-S曲线斜率基本不变,位移主要来自于锚固界面的弹性变形、鸟笼锚索的拉伸,b点荷载即为(弹性)锚固力Pe;③ 屈服强化阶段(bc):P-S曲线的斜率降低,荷载随位移继续增长,表现出(一定)强化特性,位移主要来自锚固界面的塑性变形(扩展),c点为加载极限值;④ 破坏失效阶段(cd):P-S线曲率继续降低,荷载随位移增长基本不变或降低(注:B-5&C-10因拉拔极限值超过仪器量程(450 kN),不包含此阶段)。
2) A-5 组、B-5 组、C-10 组的(弹性)锚固力为300,400 和425 kN,表明鸟笼树脂锚固在木寨岭公路隧道中具有极佳的锚固性能。
3.3 匹配性设计
3.3.1 关键参数计算
据式(5),荷载加至Pe,x=0 处剪应力即增至[τ],
对应锚固起始端此x=0 处的(弹性)位移ue(0),据式(6)计算,
另,由自由段l的弹性变形和ue(0)相加构成的拉拔端位移Se计算如下,
结合式(9)和式(11),代入β=并利用泰勒公式将得,
式(12)和式(13)中Se/Pe的取值宜采用弹性阶段的P-S曲线数据进行线性回归分析得到,记表3 为计算得到的各工况的锚固剂-围岩界面抗剪强度[τ]和剪切刚度系数Ke。

表3 锚固剂-围岩抗剪强度[τ]和剪切刚度KeTable 3 Anchorage agent-shear strength [τ] and shear stiffness Keof surrounding rock
理论上,当锚固剂与围岩均固定时,围岩-锚固剂界面的抗剪强度[τ]和剪切刚度Ke应是不变。但分析表3可知:
1) 锚固长度的变化(A-5&B-5)对[τ]和Ke均有一定影响,表现为锚固长度增加,[τ]和Ke的量值下降,在不考虑围岩变化前提下,推测施工搅拌为其主要影响因素;
2) 锚固深度的变化(B-5&C-10)对[τ]和Ke也均有一定影响,表现为锚固深度增加,[τ]和Ke的量值上升,在不考虑施工影响的前提下,推测“深部围岩(10 m)”受工程扰动影响小于“浅部围岩(5 m)”是主要原因。
综合上述分析,后续锚固长度分析中将取[τ]和Ke的最小值作为计算参数,即取[τ]=3.17 MPa,Ke=532.7 MPa;计算得到Pue=626.5 kN。
3.3.2 不同预紧力下的锚索设计参数匹配性设计
实际工程中,锚索支护系统多应用于要求预紧力达到150 kN 以上的环境,以此为基础,设定以预紧力增加50 kN 为一组工况,开展匹配性设计分析,并遵循如下设定:
1) 锚索的最终失效形式为锚固剂-围岩界面滑移,且锚固剂-围岩参数不变,即[τ]=3.17 MPa,Ke=532.7 MPa;
2) 直径<25 mm 锚索,考虑后期永久注浆保护层厚度要求,钻孔直径D=45 mm,鸟笼段平均直径d=25 mm,如此,取锚索体弹性模量Es=200 GPa,锚固剂弹性模量Em=16 GPa 时,据式(1)计算得到复合弹性模量Ea1=73 GPa。
3) 直径25~30 mm 锚索,考虑后期永久注浆保护层厚度要求,钻孔直径D=50 mm,鸟笼段平均直径d=30 mm,据式(1)计算得到复合弹性模量Ea2=73 GPa。
表4为隧道与地下工程常用单根单束预应力锚索,以表4中锚索材料性能为基础,开展木寨岭公路隧道锚索预紧力匹配性设计:1) 设定预紧力计算工况(150~600 kN),确定预应力计算控制值(200~600 kN);2) 根据计算控制值,计算不同锚索的性能发挥率β(=预紧力/Nt),要求0.85≤β<1,确定适宜锚索型号及其钻孔直径;3) 进一步根据式(9)计算得到最小(理论)锚固长度Lmin,初步分析可实施性;4) 考虑预应力超载需要[19]:预紧力≤300 kN,按25%考虑预应力加载过程损失;预紧力>300 kN,按20%考虑预应力加载过程损失,由式(9)计算考虑超载的锚固长度下限Lmin1;5) 鉴于弹性最大锚固力<极限锚固力,且采用了“先锚后注(浆黏结)”型锚索,设定α1=1.3,由式(9)计算考虑安全储备系数的锚固长度下限Lmin2;6) 由式(11)计算临界锚固长度Lc,计算考虑临界锚固长度的锚固长度上限Lmax1=0.5Lc;7) 结合现场具体施工,以及过往施工经验,设定考虑施工(搅拌)锚固效果的锚固长度上限Lmax2=2.0 m;8) 对比锚固长度Lmin1,Lmin2,Lmax1和Lmax2,得到锚固长度建议值。综合上述计算分析过程即可得到如表5中所示的匹配性设计用表。
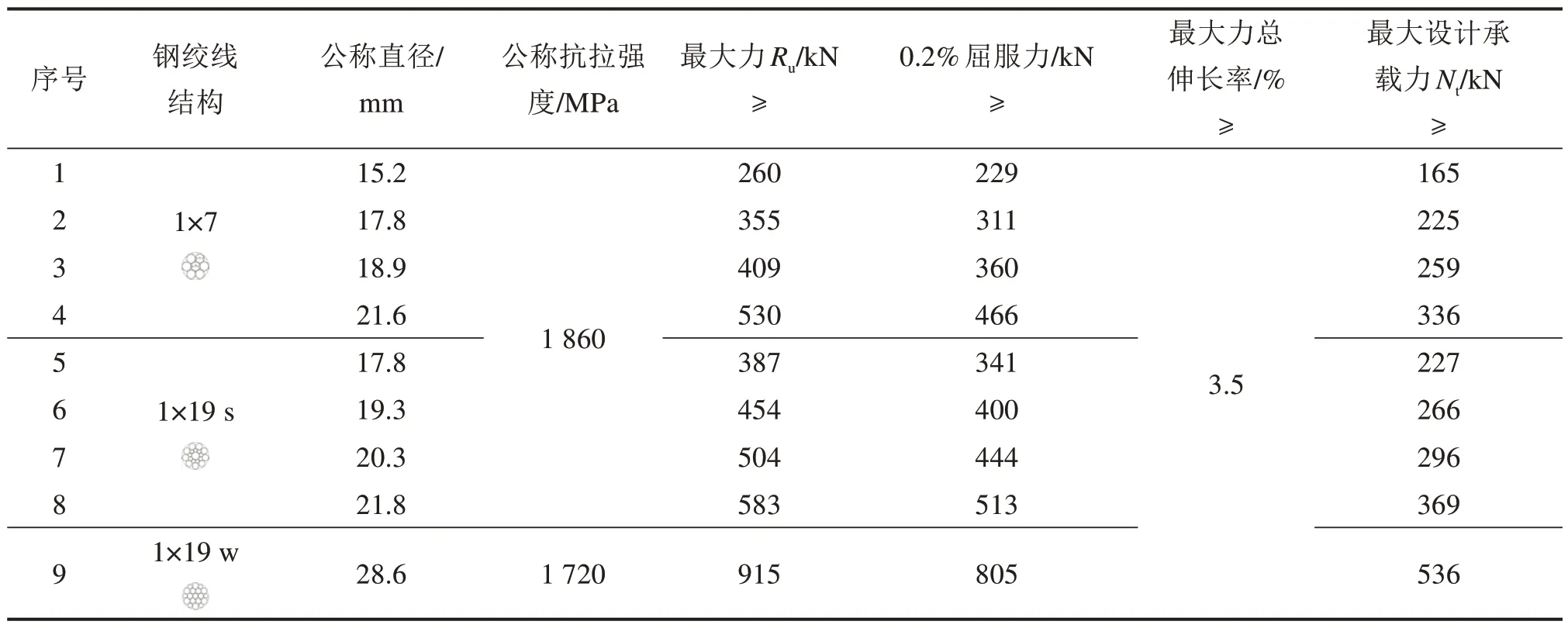
表4 隧道与地下工程中常用单根单束预应力锚索性能Table 4 Performance of single prestressed anchor cable with single bundle commonly used in tunnel and underground engineering
表5所示,木寨岭公路隧道中预应力锚索的预紧力设计不宜大于500 kN;同时,现阶段木寨岭公路隧道采用1×19 s-21.8 mm-1 860 MPa 锚索,其预紧力设计不宜大于350 kN。
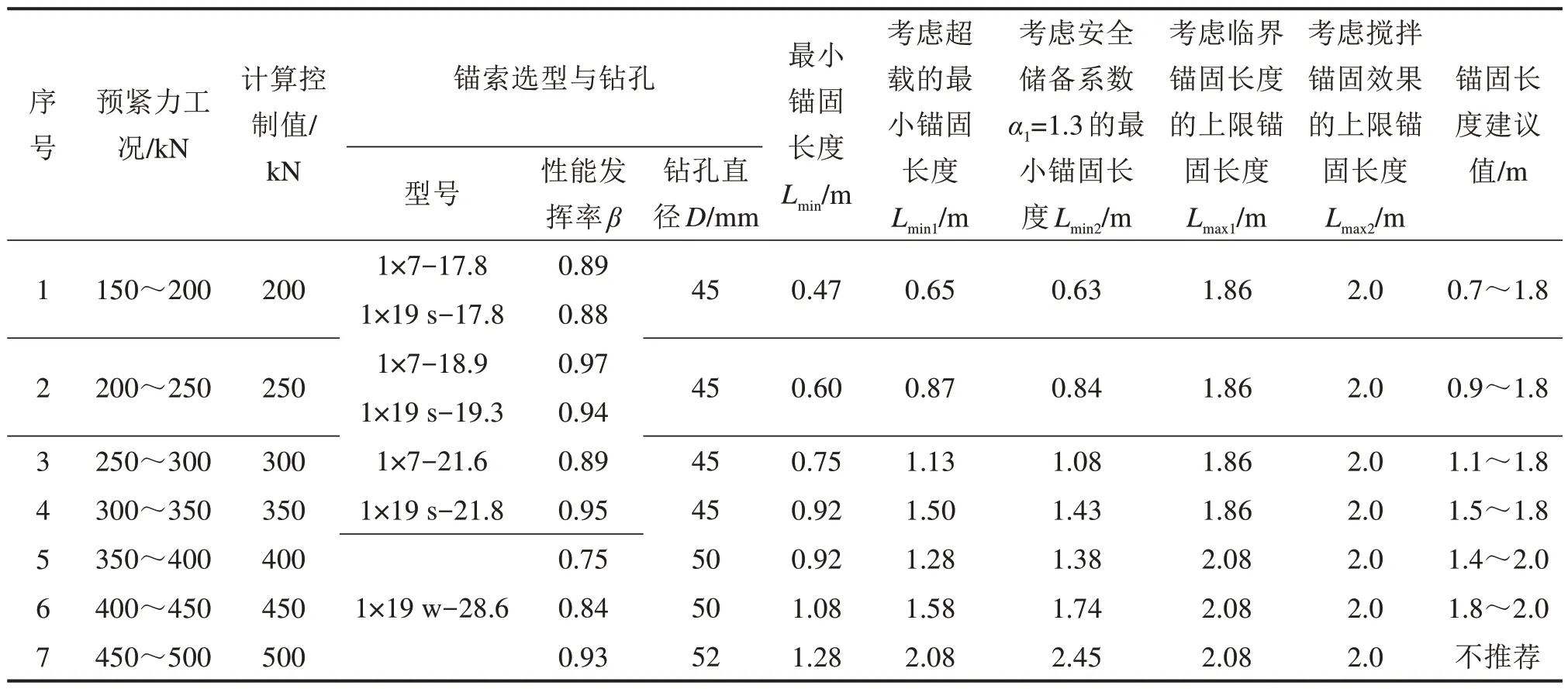
表5 木寨岭公路隧道不同预紧力下的锚索系统匹配性设计用表Table 5 Table for matching design of anchor cable system of Muzhailing highway tunnel under different preloads
4 结论
1) 以现场拉拔试验为基础,结合理论分析,提出了一种实现锚固系统预紧力与锚杆/索体型号、锚固长度相协同、匹配的设计方法,包括有:锚杆/索体型号与预紧力匹配设计、锚固可靠性设计、锚固力提升效率设计和施工锚固效果设计等4 个方面。
2) 针对锚固长度下限取值,提出了综合考虑锚固系统预应力加载过程和安全系数的计算方法;针对锚固长度上限取值,提出了综合考虑锚固力提升效率和施工锚固效果的计算方法。
3) 从锚固力与锚固长度关系出发,锚固长度超过0.5 倍临界锚固长度后,即使锚固长度增加一倍,锚固力增幅不超过10%,故而锚固长度上限值不宜超过0.5倍临界锚固长度。
4) 木寨岭公路隧道预应力锚固系统的破坏形式为锚固剂-围岩界面滑移,与理论分析中的假设相符;计算得到了适用于木寨岭公路隧道150~450 kN 预紧力的锚索型号与锚固长度范围,并建议预紧力设计不宜大于500 kN。
