“三教”改革背景下的高职数学课程体系研究——以经管类专业为例

张少凤 余 洋

宝鸡职业技术学院，陕西 宝鸡 721000

一、研究背景

2019 年1 月，国务院颁发《国家职业教育改革实施方案》，提出了“三教”（教师、教材、教法）改革的任务。“三教”改革中，教师是根本，教材是基础，教法是途径，解决了教学系统中“谁来教、教什么、如何教”的问题。传统高职数学课程教学中存在重“知识”轻“实践”现象，在数学实践与应用方面重视不够；教学还主要停留在自身的领域，没有与专业需求、技能、素养、职业道德的培育进行深度融合；与“互联网+教育”融合不全面，与其他领域知识的整合不深入，不能与时俱进。在“三教”改革的大背景下，探索如何进行高职数学教学改革显得非常重要［1］。

二、高职数学教师课程体系建设能力的提升

构建内容全面、方式灵活多样的全方位学习培训，解决高职数学教师教学能力不足的问题。在培训内容上，涵盖教学理念思路、教学设计、课程建设、教学实施和评价整个流程，加强对数学建模、数学实验及各类平台、数学软件的学习，融合数学学科的严谨、理性的思维和行业的工作态度及道德标准，提升教师教育现代化水平。在培训方式上，采用“四结合”推进：线上线下培训相结合，校内外专家指导相结合，跟踪辅导和团队研讨相结合，以改促学、以改促教、以改促研和以改促赛相结合。在培训时间上，采用“两结合”实施，固定时间和“时时可学”相结合，集体学习和个人自学相结合，制定年度培训、学期培训、日常培训计划和目标，滚动开展，压茬培训，体现培训的系统性、针对性。

三、高职数学课程体系的构建

在“三教”改革背景下，构建创新型高职数学课程实施体系，具体从课程定位、“数学+”的模块化教学内容、教学方法、课程评价四个方面进行完善和改进。形成既可以有效满足专业知识和技能成长需要，又能影响学生可持续发展能力的数学课程教育环境，培养全面发展的创新型人才［2］。

（一）课程定位

2021 年，教育部印发《职业教育专业目录》，旨在探索新的专业设置和人才培养路径，对专业的改造就是推动专业数字化和智能化。高职数学作为一门基础课程，要体现与“互联网+ 教育”“数字化”“智能化”、专业化相结合，将跨学科、趣味性、体验性、情境性、协作性、设计性、艺术性和技术性等理念有机融入不同专业高职数学课程，为学生学习专业课打下必要的数学基础，适应职业教育发展需求。

（二）教学内容

1.“数学+”模块化教学模式

以数学基本知识为基础、构建“数学+课程思政”“数学+专业案例”“数学+实验”“数学+软件知识”模块化教学模式，丰富教学内容，从根本上解决“教什么”的问题。

数学基本知识：选择函数、极限、导数、微积分的基本概念和理论，保证学生对高等数学的初步认识，以应用为目的，理解知识的结构化和关联性；再结合专业的不同，拓展与专业相关的数学知识，如经管类专业要加上级数、矩阵和统计等数学知识。拓展内容淡化繁琐的理论推导和计算，注重联系实际问题，体现“必须够用”为度的原则。

课程思政：结合相关教学内容，设计与内容相贴切的课程思政。培养学生如何从逻辑出发思考问题的数学思维。让学生在数学课的学习中，能潜移默化地感受到数学思维的魅力和培养积极的价值观、人生观和方法论。

专业案例：介绍完数学知识的原理后，适当增加专业案例。例如经济类专业增加利润、税收、最小投入、最大收益、最佳方案等与专业紧密联系的实例与练习题［3］，为将来能够适应岗位所需打好基础。

数学实验：依据学生的需求和兴趣，教师可通过选修课等方式开展数学建模、数学实验等课程，设计与专业相关的建模问题。通过小组合作的形式，反复钻研、互相切磋，寻求解决方法，得出结论，判断结论对错与优劣，使学生获得在书本和课堂上无法获得的宝贵经验和切身感受，提高学生学习数学的兴趣，培养团结协作的精神，激发创新意识。

软件知识：介绍Mathstudio、Matlab 及Spss软件在相关数学计算方面的应用，设计较简单、与专业相关的大数据问题，可与数学建模结合，在实践环节加以体现，通过利用数学软件强大的计算、绘图和分析工具，让学生感受大数据时代的智能与计算便利。

2.模块化教学内容

在现有课时不足的情况下要达到教学目的，必须要合理选取教学内容。为了实现数学教学“必须够用”“服务专业”的目标，采用数学模块化教学。以经济类专业数学课程为例。

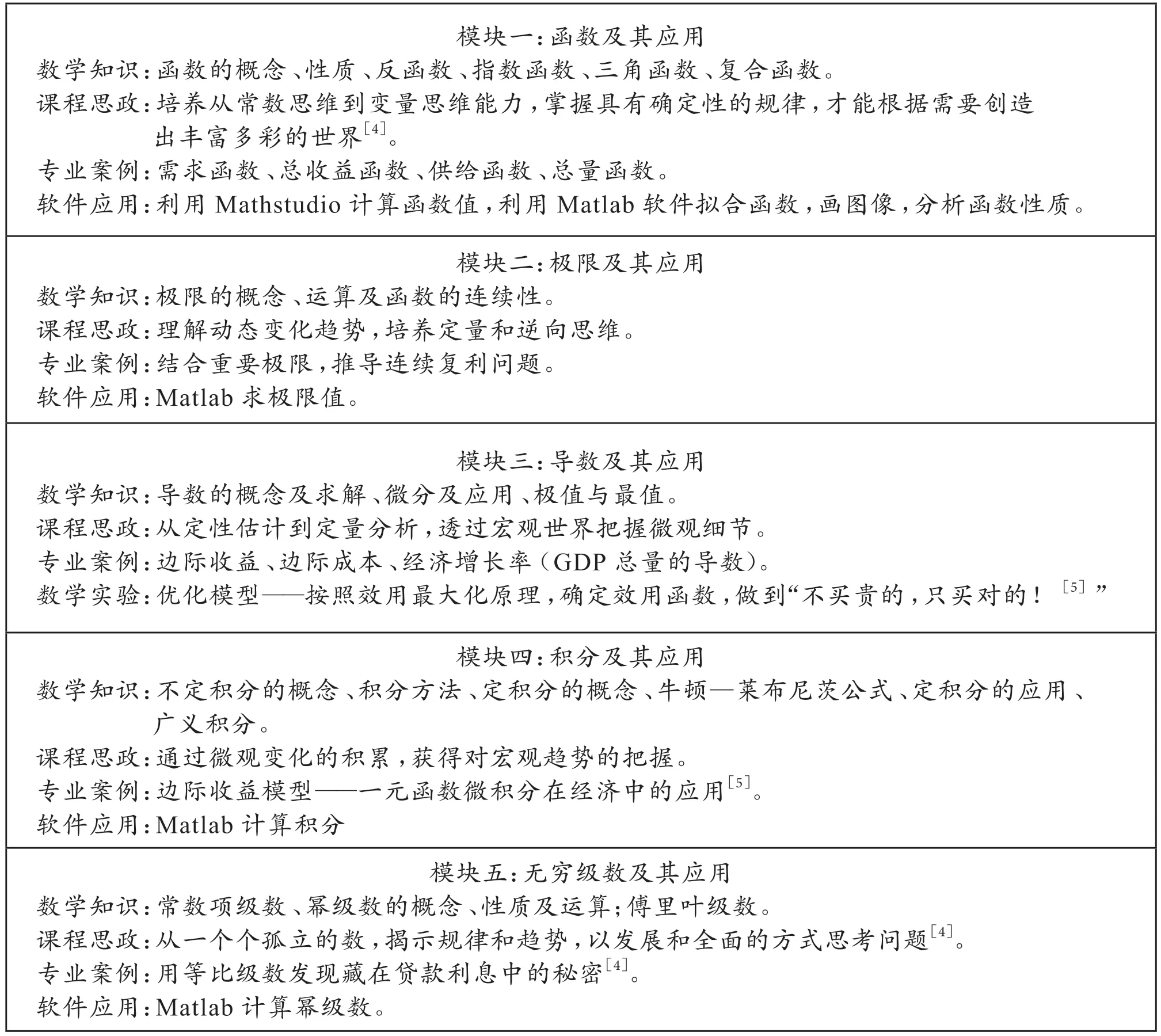
模块一：函数及其应用数学知识：函数的概念、性质、反函数、指数函数、三角函数、复合函数。课程思政：培养从常数思维到变量思维能力，掌握具有确定性的规律，才能根据需要创造出丰富多彩的世界［4］。专业案例：需求函数、总收益函数、供给函数、总量函数。软件应用：利用Mathstudio 计算函数值，利用Matlab 软件拟合函数，画图像，分析函数性质。模块二：极限及其应用数学知识：极限的概念、运算及函数的连续性。课程思政：理解动态变化趋势，培养定量和逆向思维。专业案例：结合重要极限，推导连续复利问题。软件应用：Matlab 求极限值。模块三：导数及其应用数学知识：导数的概念及求解、微分及应用、极值与最值。课程思政：从定性估计到定量分析，透过宏观世界把握微观细节。专业案例：边际收益、边际成本、经济增长率（GDP 总量的导数）。数学实验：优化模型——按照效用最大化原理，确定效用函数，做到“不买贵的，只买对的！［5］”模块四：积分及其应用数学知识：不定积分的概念、积分方法、定积分的概念、牛顿—莱布尼茨公式、定积分的应用、广义积分。课程思政：通过微观变化的积累，获得对宏观趋势的把握。专业案例：边际收益模型——一元函数微积分在经济中的应用［5］。软件应用：Matlab 计算积分模块五：无穷级数及其应用数学知识：常数项级数、幂级数的概念、性质及运算；傅里叶级数。课程思政：从一个个孤立的数，揭示规律和趋势，以发展和全面的方式思考问题［4］。专业案例：用等比级数发现藏在贷款利息中的秘密［4］。软件应用：Matlab 计算幂级数。

（三）教学实施

在教学实施方面：将线上线下混合教学、课堂内（常规、选修）与课堂外（活动竞赛、建模社团）相结合，采用多种教学方法、信息化教学手段、理实一体的教学模式（翻转课堂、小组合作、项目驱动、案例分析、数学实验等），构建一个融“理论+实践”于一体的数学教育模式和育人环境。对于理论知识，课前发布预习任务，给出问题，学生课前查找资料自学，思考，提出问题；课中教师讲解答疑，打破传统的“满堂灌”弊端，合理引导学生主动思考。对于软件操作以及建模等实践环节，采取任务驱动、小组合作的方式，通过共同讨论，团结协作解决问题，最后采用小组展示，分组点评的形式进行小结和打分。

（四）评价体系

在课程评价方面：将“知识、技能”与“可持续发展能力”评估有机融合，体现“德技并修”“育训结合”的新要求，建立包含评价对象、评价手段、评价主体、评价结论的全面、多维的课程评价体系，促使教师主动思考学习，改革教学内容，改进教学方法，提高教学质量。

学生的总评成绩主要分为三部分，第一部分为平时成绩（占25%）：线上线下学习情况、作业情况、课堂积极程度、数学软件基本应用为主；第二部分是建模成绩（占25%）：学生自由组合，三人一组，给出A、B 两套题，小组可选取任意套题，在规定期限内查找资料，根据实际做出合理假设，建立数学模型，并利用软件对模型进行求解、分析、检验、优化，最后以论文形式上交评分；第三部分是期末成绩（50%），考核学生数学基本知识，以概念、计算和基本应用为主［3］。为了推动多种形式学习成果的认定和转换，鼓励学生参加数学建模大赛，大赛成绩可以直接替换课程学分。

构建以理念先导、目标引领、内容支撑、实施检验、评价定效的“系统化”高职数学课程实施体系任重道远，要以不同专业大类对高职数学课程的需求为基准，要有永无止境学习钻研的态度，职教人的情怀、勇于实践探索的勇气和“课堂革命”的决心。星星之火可以燎原，在共同努力下，高职数学必定在育人及科技发展中发挥出更大的作用。