综合题的解题要旨：两种思维比翼，多种方法并用

徐佳丽

摘 要：综合题中含有多个知识点，具有重要的教学价值.本文提出了解数学综合题的要旨，即两种思维比翼和多种方法并用.以2023年高考数学新课标全国Ⅱ卷中一道解三角形综合题为例，从代数思维和几何思维出发探究它的多种解法，并提出若干教学启示.

关键词：解三角形；综合题；解题方法；教学启示

综合题具有重要的教学价值，因为它涉及到多个知识点，解决时会用到多种方法，因而解综合题对于学生的基础知识和基本技能的掌握、数学思想方法的运用、数学能力甚至情感态度都有较高的要求，解综合题对于学生多种核心素养有着重要的促进作用.教学中应注重培养学生解综合题的能力，要让学生做到在解题中两种思维比翼和多种方法并用，本文将以2023年高考新课标全国Ⅱ卷解三角形一题为例，说明这种解综合题的要旨.

《普通高中数学课程标准（2017年版2020年修订）》^［1］指出：学生要能借助向量的运算，探索三角形边长与角度的关系，掌握余弦定理、正弦定理.2023年高考数学新课标全国Ⅱ卷第18题是解三角形综合题，该试题考查解三角形的基础知识和基本技能，解题的本质在于将正弦定理、余弦定理、平面向量、三角形面积公式以及勾股定理相融合，寻求其中的联系，最终实现对问题的解决，考查学生数学运算、逻辑推理、直观想象的核心素养.

1 真题呈现

2 题目分析

这是一道解三角形综合题，通过给出三角形面积和中线长的相应数据，并在两个小题中分别给出一角度数及三角形两边长之间的关系，重点考查了解三角形中的基本要素问题.该题主要涉及到的知识点有：三角形面积公式、三角形中线、正弦定理、余弦定理、平面向量等；本题渗透的数学思想方法有：数形结合思想、转化与化归思想以及方程思想；本题包含的数学学科核心素养有：数学运算、逻辑推理、直观想象.

3 解法探究

3.1 基于代数思维的解题

代数思维是指通过一般化操作得到一般化结论，用符号表征数量关系，发现数学规律，解决实际问题的思维方式.

对于解三角形综合题来说，代数思维是最基本的解法，它是在正余弦定理、三角形内角和定理的基础上，将试题中的已知条件与所要求的三角形要素建立起联系，从而达到求解三角形未知要素的结果.真题题干中首先给出了三角形的面积和一条中线长，在第（1） 问中又给了附加条件，只需要从角和边的关系出发，借助正弦定理、余弦定理进行求解；在第（2）问中，给出了三角形其中两边的代数关系式，可以利用余弦定理，通过“两个互补相邻角的余弦值相反”得到方程.

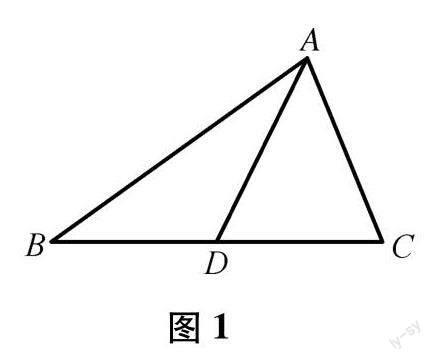
根据题意，画出草图.

3.2 基于几何思维的解法

几何思维是指通过对几何图形和空间结构的观察和分析，发现其中的规律和特点，从而解决实际问题的思维方式.

通过观察根据题意画出的图形，可以发现是“爪”形图，即连接已知三角的一个顶点与其对边的任一点所构成的图形^［2］.特殊的是，此题中所取的对边上的点是对边上的中点，因此，可以使用中线性质定理，并对该图添加辅助线使之成为平行四边形，由此将中线性质定理变形为平行四边形对角线长定理，从而想到使用向量法来解决问题.此外，单纯的几何即利用平面几何的三角形、四边形的性质也可以解决该问题.

4 教学启示

4.1 培养学生灵活的思维方式

首先，教师应充分挖掘教材中的信息，引导学生思考教材中的定理以及课后习题蕴含的数学思想方法，从而使学生更容易理解和掌握，培养学生的数学思维.教材在学生学习数学中扮演着重要角色，它是学生进行数学学习的重要工具，高考真题中蕴含的数学思维与数学思想方法最终可以在教材中找到来源.该试题第（2）问基于代数思维的解法正是来源于人教版《普通高中教科书数学》必修第二册A版（2019年版）第53页第15题，根据两个互补相邻角的余弦值相反，两次活用余弦定理来证明结论，证明出的结论正是中线性质定理.同时，学生在学习《平面向量》这一章时，频繁接触到“爪形”三角形，知道“爪形”三角形常与三角形的角平分线、中线、高、三等分点相结合，而且教材中用向量法来推导了余弦定理，教师可以因势利导，将平面向量与解三角形综合题相结合，帮助学生从几何思维来分析看待解三角形问题.

其次，在教学中，教师可以利用波利亚解题思想，问题呈现方式应当尽可能地培养学生灵活的思维方式.美国数学家波利亚在他的著作《怎样解题》中，给出了著名的“怎样解题表”，在怎样解题表中，又给出了理解题意的提示语：“未知量是什么”“已知数据是什么”“条件是什么”，还给出了“盯住目标”“回到定义中去”“你以前见过它吗”“有什么方法可以利用”等等常见的解题提示语^［4］.在该类试题中，教师应引导学生，首先理解题意，明确题中所给的条件与需求的未知量分别是什么；教师再进行引导性提问：从三角形面积中可以得到怎样的数量关系？角与边的关系一般利用什么知识和方法来解决？根据角和边的大小可以列出怎样的代数式？你以前在哪见过这种图形？三角形的中线有什么几何性质？你还可以利用什么方法来解决？对于这些问题，学生可能给出的结论多种多样，但都是基于代数思维和几何思维进行思考，探究如何通过这两种思维解决问题，同时关注到解三角形既是函数和代数的，又是几何的.

最后，教师要加强解三角形专题模块复习，在实际的问题解决中，帮助学生形成解三角形综合题的解题思路，提升学生知识迁移应用能力，培养学生的代数思维和几何思维.通过梳理近几年高考真题中解三角形综合题，不难发现，重点考查正余弦定理的直接应用；求三角形的边、角；三角形边长、周长、面积的取值范围；嵌套三角形求解问题等^［3］.教师在进行专题模块复习时，应首先将与解三角形相关的知识进行复习，如函数、三角函数、向量等基础知识；其次，让学生在解題时养成两种思维比翼的习惯，做到多种方法并用.弄清楚有什么条件，要求什么问题，先考虑正余弦定理是否能解决问题，有中点就联想到中线、中位线，有特殊角就构造含特殊角的直角三角形；最后，根据学生自身情况布置相应的习题，鼓励学生结合实际情况选择合适的定理进行解题，最终使学生形成解三角形综合题的解题思路.

4.2 使得学生养成一题多解的习惯

一题多解本质上就是学生从条件出发找到联系条件和结论的不同的路径，使得学生养成一题多解的习惯，对于提升学生包括创造性思维在内的思维能力具有积极的意义.当学生面对解综合题时，找到解决问题的不同解法，能有效培养学生多种思维能力.因此，教师应在教学中加强一题多解训练，引导学生基于条件进行合理的联想，寻找解题的突破口.

以此试题为例，上述的几种解法都是基于对试题条件的分析，从代数和几何思维出发探寻破解路径.第（1）问中，注意到角B既是△ABC的内角，又是△ABD的内角，所以tanB可以在这两个三角形中求解.第（2）问中，给出了b，c的代数关系，要求b，c，就将问题转化为再找一个有关b，c的关系式.

从代数思维切入，第（1）问，中线将△ABC一分为二，为两个面积相同的三角形，由其中一个三角形面积求出a，再由中点与∠ADC的值，将BD与∠BDA放到△ABD中，已知三角形的两边长与一个内角，自然想到解法一；中线将△ABC一分为二，已知公共边长和相邻角的值，自然联想到分别在两个小三角形中使用余弦定理求出b，c，进而在△ABC中，已知三角形三边长，得到tanB，即解法二；a的值除了能在小三角形中求得，还能借助正弦定理与三角形面积公式求出，在△ABD中，利用余弦定理得到tanB，即解法三.第（2）问中，通过“两个互补相邻角的余弦值相反”的结论得到方程，求出a，再由已知条件发现AD既是中线又是高线，由三线合一求解，即解法一.

从几何思维切入，第（1）问中，tanB可以直接在直角三角形中求得，因此联想到通过作高构造直角三角形，即解法四.第（2）问中，根据前面学过的平面向量知识，利用向量法将∠BAC的余弦值用b，c表示出来，又利用三角形面积公式，用b，c表示∠BAC的正弦值，由同角三角函数的基本关系得到b，c关系式，即解法二；已知三角形两边长的平方和以及中线长，又联想到构造平行四边形，得到三角形另一边长a，由余弦定理与三角形面积公式得到b，c关系，即解法三；由b²与c²联想到构造直角三角形，利用勾股定理得到b，c关系，即解法四.

在解三角形综合题中，除了借助三角形的中线来构建对应边长之间的关系，还可以借助三角形的角平分线、三角形的高来构建对应线段的比例关系.教师可以通过改变题目的条件、问题呈现方式，但不改变题目的本质，引导学生独立思考，利用代数思维和几何思维来处理解三角形问题.实际上，对于高中许多综合题来说，都会涉及到这两种思维.在教学中，教师可以将这两种思维渗透到日常教学中，启发学生积极思考，借助典型例题，探求一题多解的方法，在培养学生思维广阔性的同时，培养学生数学核心素养，开拓并发展学生的代数与几何思维.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］ 劉海涛，张大伟.活跃在2023年高考卷中的“爪形”三角形［J］.中学数学研究（华南师范大学版），2023（17）：1-3+53.

［3］ 黄春霜，彭永婷.2021年数学新高考Ⅰ卷解三角形综合题的特点与教学启示［J］.中学理科园地，2023，19（5）：94-96.

［4］ （美）G.波利亚.怎样解题［M］.上海：上海科技教育出版社，2011.

［5］ 韦道田.巧思维解题，妙方式推广——对一道解三角形题的应用的研究［J］.数理天地（高中版），2023（23）：25-27.

［6］ 计春玲，吴庆龙，许雪莲.高中数学新教材人教A版与B版“解三角形”内容的比较研究［J］.理科考试研究，2023，30（19）：20-22.