一种抑制控制力矩陀螺框架电机共模电压的方法*

菅 宇，潘 蕊，王 洁，杨冬雷，蔡树文

(上海航天控制技术研究所·上海·201109)

0 引 言

随着航天技术的进步，航天器的种类日渐增多，功能越来越集成化，目前研制高精度、高稳定性、长寿命的大型航天器是一个必然的发展趋势[1]。姿控系统作为航天器分系统中非常重要的一个子系统，是评判航天器性能的重要标准。姿控系统由姿态敏感器机构、执行机构以及控制机构组成。目前，大多采用控制力矩陀螺作为执行机构[2]，它具有力矩放大能力，在同等质量和体积下可以提供比飞轮高一个数量级的控制力矩。

控制力矩陀螺主要由高速转子系统、低速框架系统和基座组成，主要的运动部件有高速转子系统和低速框架系统，通过大惯量转子高速旋转获得角动量，框架转动改变转子系统的角动量矢量产生输出力矩[3]。其中，永磁同步电机具有功率密度大、效率高、振动小等优点，一般作为控制力矩陀螺的低速框架部分。但是，依据永磁同步电机的机械结构，在正常运行过程中，电机的轴承与润滑剂之间存在相互作用，这一部分可以被等效为一个电容，共模电压通过的机械连接对这个等效电容进行充电，形成轴电流，对轴承造成侵蚀影响使用寿命，进而影响航天器的整体寿命[4-6]。

共模电压抑制[7]主要有两种途径：一是基于硬件方面，通过增加滤波器或改进驱动器拓扑结构来实现；二是基于软件方面，优化驱动器的控制算法来实现。文献[8]中使用共模滤波器，抑制了系统中的共模传导干扰，有效地降低了共模电压对设备的影响，但是只对特定载波频率生效。文献[9-10]中提出了一种双桥逆变器拓扑结构，两组逆变器分别输出极性相反的控制电压，通过共模电压对消实现抑制效果，但这种拓扑结构使用的开关器件数量加倍，电路成本及损耗翻倍，同时还存在两组逆变器控制同步的问题。文献[11]提出了AZSPWM算法，利用参考矢量所在扇区的两个相邻矢量和其中一个矢量的反相有效矢量来进行调制，但是会在输出电压中引入较多谐波分量。文献[12]提出了NSPWM算法，这种算法使用三个相邻的有效电压矢量来进行调制，但是这种算法存在失效区域，仅在调制比m>0.770时有效。文献[13]提出了一种RSPWM控制算法，使用三个相差120°的有效矢量进行控制，可将共模电压保持为一固定数值，消除系统中的漏电流，但是母线利用率只有常规算法57.7%。

本文通过优化传统驱动器的拓扑结构和常规的PWM控制算法，提出了一种基于三相四桥臂与优化的SVPWM调制算法结合的共模电压抑制策略，这种共模电压抑制策略，在调制过程中避免零矢量的使用，通过计算分析得到优化算法的开关状态分布与作用时间，结合四桥臂的拓扑结构可以使系统处于平衡状态，实现对共模电压的有效抑制。

1 共模电压产生机理

目前，一般使用两电平电压型驱动器来驱动永磁同步电机，在进行共模电压产生机理分析时，可以从单相驱动器拓扑结构入手，之后将结果推广至多相驱动器拓扑结构。

单相驱动器拓扑结构共有两种输出状态：一种为差模状态，如图1所示；另一种为共模状态，如图2所示。

图1 单相逆变器的差模输出状态Fig.1 The differential-mode output state of single-phase inverter

图2 单相逆变器的共模输出状态Fig.2 The common-mode output state of single-phase inverter

当功率器件S1与S4或S2与S3同时开通时，驱动器处于差模输出状态，负载两端的电压UUV与母线电压Vdc相同；当功率器件S1与S2或S3与S4同时开通时，驱动器处于共模输出状态，负载两端的电压UUV为零。在单相驱动器中，共模电压的定义为：各桥臂输出的中点与地之间的电压差，如式(1)所示。

(1)

式中，Vcom为系统的共模电压，VU，VV分别为U，V点的电压。

将单相驱动器的共模电压定义推广至多相驱动器，图3所示为常规多相驱动器的基础拓扑结构。在图3中，O为驱动器直流侧电压的中点，一般情况下将该点设置为零电位点，N为负载的中性点，A，B，C，…，M为驱动器各桥臂输出的中点，vMN为M相桥臂输出的相电压，vAO，vBO，vCO，…，vMO为驱动器各桥臂输出中点与直流侧电压中点O之间的电压差，ia，ib，ic，…，im为各桥臂的相电流。因此可以得到多相驱动器的共模电压Vcom为驱动器直流侧电压中点与电机绕组的中性点的电压差。

图3 多相逆变器的一般拓扑结构图Fig.3 The general topology of the multiple-phase inverter

多相驱动器各桥臂的相电压存在如式(2)所示的电压关系

(2)

将式(2)中的各式相加，可以得到

mvNO=vAO+vBO+…+vMO-R(ia+ib+…+

(3)

在使用Y形绕组结构的电机中，各相相电流的关系如式(4)所示

ia+ib+ic+…+im=0

(4)

将式(4)代入式(3)中，可以得到对于一般多相驱动器的共模电压Vcom的表达式为

(5)

由式(5)可知，两电平驱动器的共模电压Vcom为直流侧电压的中点与各桥臂的输出中点之间电压差的平均值。当各相相电压处于对称状态时，驱动器的共模电压为零。永磁同步电机控制系统中，驱动器一般使用SVPWM调制算法。在这种调制算法下，各相相电压为幅值相同、宽度不同的电压脉冲，运行过程中电压脉冲不会始终维持在对称状态，会在系统中引入共模电压。电压脉冲由各桥臂的开关状态所决定，所以可以将系统的共模电压Vcom用各桥臂的开关状态表示。用Si来表示驱动器第i相桥臂的开关状态，其中i=A，B，C，…，M。当上桥臂开通下桥臂关断时，Si=1，此时第i相桥臂对直流侧中点的输出电压为+Vdc/2；当上桥臂关断下桥臂开通时，Si=0，此时第i相桥臂对直流侧中点的输出电压为-Vdc/2。

所以，对于多相驱动器来说，共模电压Vcom的表达式可以进一步表示为

(6)

图4所示为三相三桥臂驱动器的拓扑结构，由式(6)可知，三相三桥臂驱动器的共模电压可以表示为

图4 三相三桥臂驱动器的拓扑结构图Fig.4 The topology of the three-phase three-bridge inverter

(7)

由式(7)可知，三桥臂驱动器在任意时刻的输出相电压均不满足对称条件，共模电压会在±Vdc/6和±Vdc/2之间波动，这样的共模电压使用传统的滤波器很难消除，为了消除电路不对称的工作状况，需要对驱动器的拓扑结构进行优化。

在本文中，选择采用三相四桥臂驱动器的拓扑结构来抑制系统的共模电压，拓扑结构如图5所示。只要保证四桥臂驱动器中任意时刻都有两个上桥臂的开关器件导通，两个下桥臂的开关器件导通，就可以使各桥臂输出的相电压保持对称状态，消除系统中的共模电压。

图5 三相四桥臂驱动器的拓扑结构图Fig.5 The topology of the three-phase four-bridge inverter

2 优化的SVPWM算法的共模电压抑制方法

在常规的SVPWM调制算法中，载波是频率与开关频率相同的三角波，基波为三相对称的正弦波，比较过程中，只要在载波的峰值附近，就会出现三相电压同时为+Vdc/2或-Vdc/2的情况，即零状态。在零状态出现的时刻，无论如何控制第四桥臂，都不会使系统处于对称状态。

四桥臂驱动器的拓扑结构中，新增的第四桥臂需要通过三维的空间矢量重新规划各扇区的矢量。首先需要根据式(8)将系统由a-b-c坐标系转化到α-β-γ坐标系下

Xαβ0=Tabc/αβ0Xabc

(8)

式中，

经过坐标变换之后，可以得到四桥臂驱动器的电压矢量分布图，如图6所示，共有16个空间电压矢量，其中14个为有效电压矢量，2个为零矢量。

图6 三相四桥臂的电压矢量分布图Fig.6 The voltage vector distribution diagram of the three-phase four-bridge inverter

为了消除系统的共模电压，需满足任意时刻都有两个上桥臂开通，两个下桥臂开通，第四个桥臂的状态可以依据前三桥臂的开关状态确定。在这种情况下，能实现消除共模电压的只有γ=±2/3时两个平面上的六个有效矢量。这六个有效矢量γ的模是固定值，所以可以将三维的开关矢量图转化为平面的矢量图，如图7所示。

图7 三相四桥臂的有效电压矢量分布图Fig.7 The effective voltage vector distribution diagram of the three-phase four-bridge inverter

每个电压矢量所对应的开关状态与常规SVPWM调制算法中的开关状态相同，只是增加了对第四桥臂的控制。当前三桥臂的开关状态确定后，第四桥臂的开关状态也被确定，其控制信号可由式(9)得出

(9)

在常规的SVPWM调制算法中，由于零矢量的存在，即使在驱动器拓扑中加入了第四桥臂，系统的共模电压依然会在±Vdc/4之间波动。为了使驱动器始终处于对称状态，需要避免零矢量的使用。在本文中，采用与有效矢量Vr相邻的两个大小相同、方向相反的有效矢量来代替零矢量，即在一个开关周期中使用4个有效矢量进行调制。以参考矢量Vr位于第I扇区为例，有效矢量选择用V1和V2，再选择与之相邻的两个矢量V3和V6来代替零矢量，实现对常规SVPWM调制算法的优化。

由于使用了4个有效矢量来进行调制，需要重新分配各扇区内有效电压矢量的顺序及作用时间。以参考矢量Vr位于第I扇区为例，选用V1，V2，V3和V6这4个有效矢量进行控制，设T1，T2，T3和T6分别为电压矢量V1，V2，V3和V6的作用时间，在一个开关周期Ts内满足如下关系

T1V1+T2V2+T3V3+T6V6=TsVr

(10)

T1+T2+T3+T6=Ts

(11)

式(10)为α-β-γ坐标系下的方程，展开后可以得到

(12)

式中，

将上述结果代入式(11)，可得

(13)

式中，θ为参考矢量Vr与有效矢量V1的夹角。

求解后可以得到

(14)

在实际的应用过程中，时间T1，T2，T3和T6均必须满足大于零的约束条件，可以得到调制比m

(15)

在实际的应用过程中，为了使式(14)在任意的θ均成立，可以得到算法的调制比m≤1。从理论上来说，优化的SVPWM算法虽然可以实现对共模电压的抑制，但是母线电压的利用率下降，同时器件的开关损耗也会增加。

在优化的SVPWM调制算法中，是通过两个大小相同、方向相反的矢量来代替零矢量作用，因此这两个矢量的作用时间相同，即T1=T6。在实际应用中为简化运算，可以利用式(14)得到有效矢量的时间T2和T3，之后与开关周期做差来求得替代矢量的作用时间。图8所示为在第I扇区内，各桥臂的开关切换状态与时间分配情况。

图8 第I扇区开关状态Fig.8 The switch status of the Sector I

3 仿真试验及结果分析

在仿真验证过程中，分别搭建三桥臂驱动器与四桥臂驱动器。设置直流母线的电压Vdc为30V，功率模块的开关频率为20kHz，使用常规的SVPWM调制算法分别驱动三桥臂驱动器和四桥臂驱动器，可以得到仿真波形如图9和图10所示。

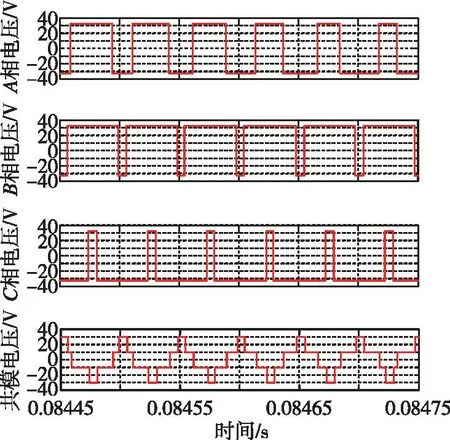
图9 使用常规的SVPWM调制算法的三桥臂逆变器电压波形与共模电压波形Fig.9 The phase voltage and common mode voltage of the conventional SVPWM algorithm and three-bridge inverter

图10 使用优化的SVPWM调制算法的三桥臂逆变器电压波形与共模电压波形Fig.10 The phase voltage and common mode voltage of the improved SVPWM algorithm and three-bridge inverter

从图9和图10中可以看出，采用常规的SVPWM调制算法时，三桥臂驱动器的共模电压在±Vdc/2之间波动，四桥臂驱动器的共模电压在±Vdc/4之间波动。由此可见，四桥臂驱动器对共模电压有一定的抑制效果，但是调制算法使用了零矢量，无论第四桥臂如何调节都不能完全抵消不对称状态，因此还需要对调制算法进行优化。

使用改进的SVPWM调制算法分别驱动三桥臂驱动器和四桥臂驱动器，可以得到如图11和12所示的仿真波形。

图11 使用常规的SVPWM调制算法的四桥臂逆变器电压波形与共模电压波形Fig.11 The phase voltage and common mode voltage of the conventional SVPWM algorithm and four-bridge inverter

图12 使用优化的SVPWM调制算法的四桥臂逆变器电压波形与共模电压波形Fig.12 The phase voltage and common mode voltage of the improved SVPWM algorithm and four-bridge inverter

通过图11和图12，采用改进SVPWM调制算法后，避免了零矢量的使用，三桥臂驱动器的共模电压在±Vdc/6之间波动；四桥臂驱动器在任意时刻均有两个上桥臂导通，两个下桥臂导通，系统始终保持在平衡的状态，共模电压为零。由此可见，将两种共模电压抑制的方法结合可以有效地抑制系统中的共模电压。

4 结 论

本文分析了单相逆变器的共模电压产生机理，并将结果推广到多相逆变器，提出了一种基于三相四桥臂驱动器拓扑结构与优化的SVPWM调制算法结合的共模电压抑制策略，通过计算分析得到优化算法的开关状态分布与作用时间，最后通过仿真试验结果分析可知：三相三桥臂驱动器中，优化算法的共模电压虽然小于常规调制算法，但是由于拓扑结构的限制，系统中不存在平衡状态，共模电压始终存在；三相四桥臂驱动器中，常规调制算法由于零矢量的使用，如何控制第四桥臂都不能使系统处于平衡状态，如不考虑死区时间的影响，优化的调制算法可以使系统时刻处于平衡状态，共模电压为零。