基于解析模型的永磁同步电机优化设计
2023-03-19朱托,李正,张凯,李孜
朱 托,李 正,张 凯,李 孜
(上海理工大学 机械工程学院,上海 200093)
永磁(Permanent Magnet,PM)电机因为其高能量密度和高效率的特性,被越来越广泛地应用在高速电机、电动汽车等领域[1-2]。永磁电机的效率是一个关键设计参数,而损耗计算则是设计该电机的基础[3]。永磁体的周向分块分段是较为常见的电机设计,在计算损耗时,在极坐标系下无法使得每段永磁体截面上的总涡流为零[4]。文献[5~7]在二维直角坐标系下计算了转子的涡流损耗,考虑了永磁体的周向分段。文献[8~9]采用镜像法建立三维解析模型,该模型能考虑永磁体的轴向分段和周向分段。相较于文献[5~6],文献[7~9]虽然精度更高,但模型较为复杂,难以应用。文献[10~11]使用有限元(Finite Element Analysis,FEA)研究永磁体电阻率、铜屏蔽层厚度对涡流损耗结果的影响。文献[12]在计算转子涡流损耗时,比较了时步有限元和时谐有限元两种方法,并认为后者可作为前者的高效替代方案。然而,有限元法求解效率较低,且不易看出各变量间的关系。
电磁转矩是电机的另一关键参数。文献[13~14]使用解析法计算了Halbach阵列永磁电机的电磁转矩。文献[15~16]在解析法的基础上对永磁体磁极形状参数进行优化,其中文献[16]使用粒子群优化算法(Particle Swarm Optimization,PSO)进行求解。
在研究永磁同步电机(Permanent Magnet Synchronous Machine,PMSM)解析模型时,很少有文献能同时求解涡流损耗和电磁转矩这两种指标。本文依次推导出以上两种磁场解析模型,并对比了解析解和时步有限元的数值解。在对定子绕组节距和永磁体极弧系数进行参数影响研究后,使用粒子群算法进行优化迭代,使得电机设计能同时实现降低损耗和提高转矩等多种目标。
1 电机模型和参数
1.1 电机模型
电机模型为六相12槽14极永磁同步电机,AUBVCW这六相绕组在空间上对称分布,通电时序互差60°电角度[17]。电机的截面图如图1所示。
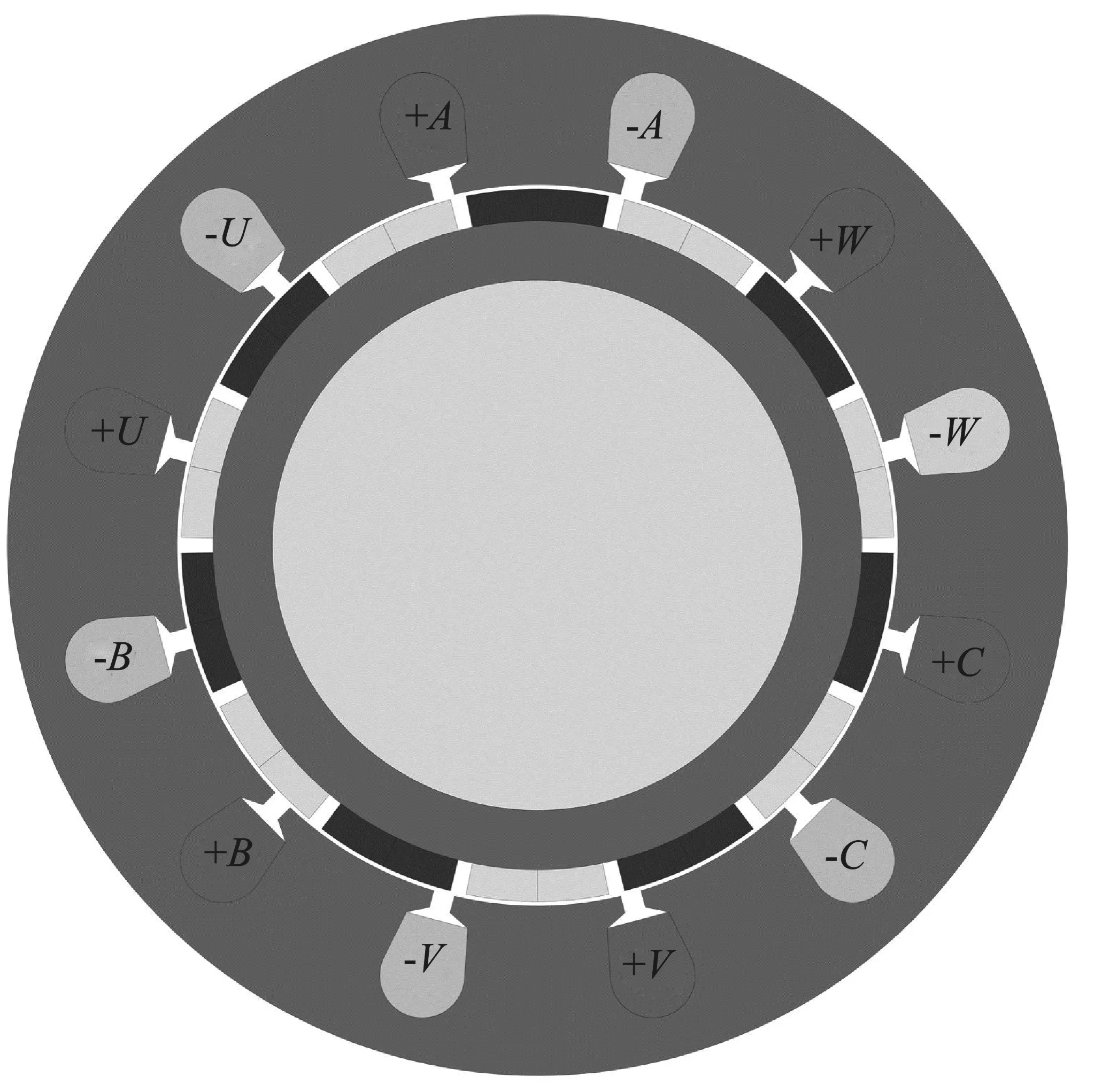
图1 六相12槽14极永磁同步电机截面图Figure 1. Cross-sectional schematic of a 6-phase 12-slot 14-pole PMSM
解析模型在图1的基础上增加了保护套计算域。
1.2 简化假设
对于电机的电枢反应磁场和空载磁场模型,作如下假设:
(1)将气隙、保护套和永磁体区域看作半无限平面;
(2)忽略端部效应,感应涡流只有轴向分量;
(3)各个媒质是均匀且各向同性的,其电导率σ、磁导率μ是不变的常数;
(4)定子和转子铁心磁导率无穷大,电导率为0,忽略定子和转子铁心中产生的涡流;
(5)忽略定子槽域、槽口域,即忽略空载涡流损耗和齿槽转矩;
(6)对于电枢反应磁场,定子绕组电流由分布在定子槽开口的等效电流片模型表示;
(7)解析模型均在二维直角坐标系下,即空载磁场中永磁体平行充磁和径向充磁等同。
1.3 电机参数
电机参数如表1所示。其中定子绕组的输入电流均为理想的交流电,计算数据时忽略保护套。
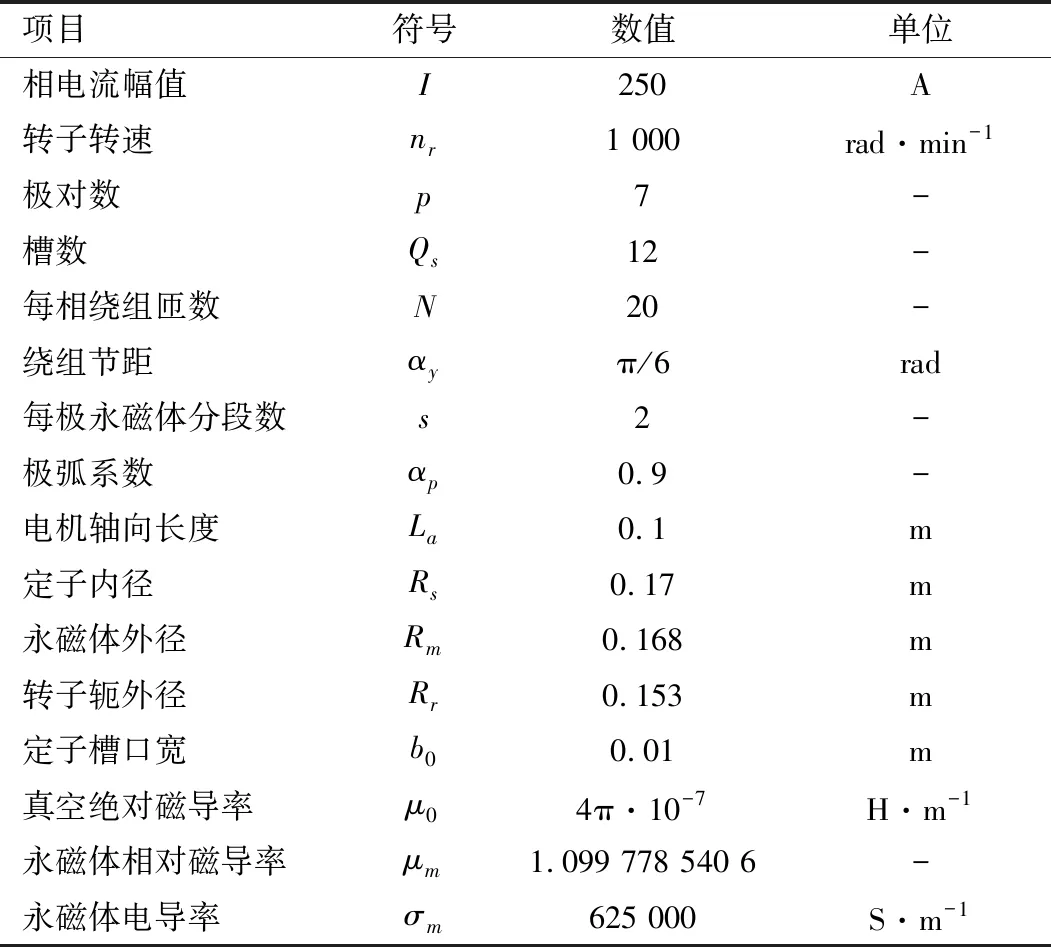
表1 结构数据和参数
2 电枢反应磁场解析模型
电机的电枢反应磁场计算模型如图2。
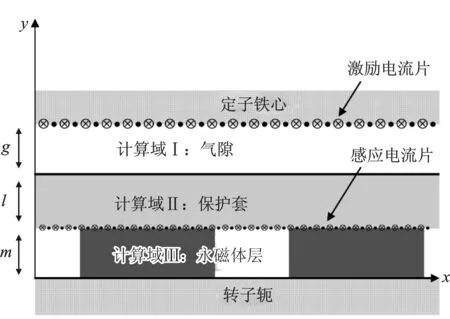
图2 电枢反应磁场计算模型Figure 2.Calculation model of armature reaction magnetic field
如图2所示,电枢反应磁场模型中,电机周向为x轴,径向为y轴。计算域共3层,从上到下依次是厚度为g的气隙域、厚度为l的保护套域和厚度为m的永磁体域,每个计算域均有对应的电导率和磁导率。电枢反应磁场模型将永磁体电密在厚度上积分成永磁体顶层的感应电流片,以此来考虑涡流反应。
在永磁体域这一层中,由于解析模型考虑了永磁体的周向分段,因此当永磁体极弧系数小于1时,各极永磁体间会存在气隙。
2.1 等效电流片模型
考虑定子绕组排布的空间v次谐波和定子电流时间k次谐波,A相电流片表达式为

(1)
式中,ia是A相电流瞬时值,为∑Ikcoskpnrt;ksov是槽口系数,为sin(vb0/2Rs)/(vb0/2Rs);kpv是节距系数,为sin(vαy/2);kdv是分布系数,为1;kwv是绕组系数,为kpv×kdv。
对称六相绕组的合成等效电流片为
J=JA+JB+JC+JU+JV+JW=
(2)
式中,Jkv是谐波幅值,为6NIkksovkwv/(πRs)。
当k≠3n,将式(2)变形如下
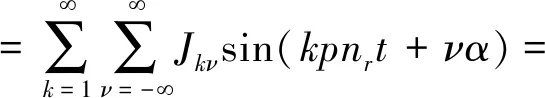
(3)
式中,β为vπ/τ;τ为所有计算域中心高度所对应的一对极对应极距(基波极距)。
将定子静止坐标x转化为转子旋转坐标xr,转换式为πx/τ=nrt+πxr/τ。所以式(3)改写为
(4)
电枢反应场中横坐标均为转子旋转坐标。
2.2 电枢反应磁场控制方程及通解
在电枢反应磁场中,气隙域的上边界是代表定子磁动势的电流片。
2.2.1 气隙域
(5)
(6)
由定子电流片激励,式(5)的通解为
(7)
式中,A、B是由边界条件确定的常数。
磁通密度的切向和径向分量为
(8)

2.2.2 保护套域
(9)
通解为
(10)
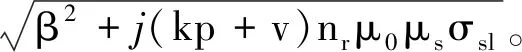

[CeλⅡy+De-λⅡy]cos[(kp+ν)nrt+βx]
(11)
2.2.3 永磁体域
为考虑永磁体的周向分段,假设每一块宽度为bM的永磁体块被分为s段。永磁体块的编号为ρ(ρ=1,…,2p),分段编号为λ(λ=1,…,s),则任一永磁体块的任一段记作(λ,ρ),在永磁体分段内的x轴坐标为
(12)
式中,τpM是永磁体高度中间点所对应半径上的极距,为π(Rm+Rr)/2p;bM是永磁体高度中间点所对应半径上的宽度,为αpτpM。
在永磁体中,为考虑涡流反应,在y=m处,定义感应电流片AⅢisin[(kp+v)nrt+βx]。这种近似避免了因为x轴方向上材料的不连续分布,而导致在计算边界条件时出现过于复杂的情况。
由于引入感应电流片,永磁体域内的λⅢ用β代替。此时永磁体域周向磁位参考式(7)为
(13)
式中,E、F是由边界条件确定的常数。
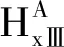
永磁体域轴向电密为
(14)
式中,JⅢc是附加电流项,其使每个永磁体块段内电密积分为零。式(14)只在永磁体段内有效。
关于感应电流片参数AⅢi求取,可参考文献[5]。
2.3 计算域间边界条件
电枢反应磁场边界条件如下:
当y=g+l+m,有
(15)
当y=l+m时
(16)
当y=m,则有
(17)
当y=0,则有
(18)
将各计算域x方向上的磁场强度和y方向上的磁密代入式(15)~式(18),求得待定常数A、B、C、D、E和F。
2.4 涡流损耗求解
由式(14)可知,对于任一永磁体段(λ,ρ),在一个电周期T=2π/(pnr)内的平均涡流损耗为
(19)
式中,La为永磁体轴向长度。
每一个永磁体段(λ,ρ)内的涡流损耗功率相等,则永磁体的总涡流损耗为
PⅢ=2psPⅢ,λρ
(20)
在保护套中,由式(11)得到在一个电周期T=2π/(pnr)内的平均涡流损耗为
(21)
式中,τpS为保护套高度中间点所对应半径上的极距。
3 空载磁场解析模型
电机的空载磁场计算模型如图3所示。

图3 空载磁场计算模型Figure 3. Calculation model of no-load magnetic field
在图2中,电枢反应磁场有电枢电流片激励,有永磁体涡流,无永磁体励磁。在图3中,空载磁场无电枢电流片激励,无永磁体涡流,有永磁体励磁。
3.1 空载磁场控制方程及通解
在空载磁场中,作为励磁源,首先求解永磁体域,空载磁场均在静止坐标系下求解。
3.1.1 永磁体域
永磁体中磁密B、磁场强度H和磁化强度M满足下式。
B=μ0M+μ0μmH
(22)
计算永磁体域时,不考虑齿槽以及其引起的空载涡流损耗,即永磁体中无电流密度分布。由磁矢定义可得关于轴向磁位的泊松方程为

(23)
式中,Mx为永磁体磁化强度切向分量;My为永磁体磁化强度径向分量。
由文献[18]可知
(24)
式中,Mxn为0;Myn为4pBrsin(nπαp/2p)/(nπμ0);θv为永磁体初始位置;Br为永磁体剩磁。
令γ=nπ/τ,将式(24)代入式(23)可得
(25)
式(25)通解为
(26)
式中,Y、Z是由边界条件确定的常数。
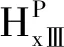
3.1.2 保护套域
计算保护套域时,同样不考虑空载涡流损耗。其中的磁场控制方程为拉普拉斯方程。保护套域轴向磁位的通解由式(25)可得
(27)
式中,W、X是由边界条件确定的常数。
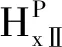
3.1.3 气隙域
气隙域磁场控制方程为拉普拉斯方程。气隙域轴向磁位通解如下
(28)
式中,U、V是由边界条件确定的常数。

3.2 计算域间边界条件
空载磁场边界条件如下
当y=g+l+m
(29)
当y=l+m
(30)
当y=m
(31)
当y=0
(32)
将各计算域x方向上的磁场强度和y方向上的磁密代入式(29)~式(32),可求得待定常数U、V、W、X、Y和Z。
3.3 电磁转矩求解
由式(7)、式(8)可知,在静止坐标系下,电枢反应磁场中气隙磁密的切向和径向分量为
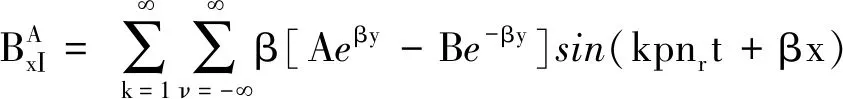
(33)
(34)
由式(28)和式(8)可知,空载磁场中,气隙磁密的切向和径向分量为
(35)
(36)
负载磁场中,气隙磁密的切向和径向分量为式(37)。
(37)
由麦克斯韦应力张量法计算电磁转矩,积分路径为气隙厚度中心位置处,即Rint=(Rm+Rs)/2。电磁转矩表达式为
(38)
由表(1)电机输入参数和式(38)可知,平均电磁转矩Tave和电磁转矩波动幅值ΔTvn为
(39)
(40)
式中,Cxav、Cyav、Cxpn和Cypn是电枢反应磁场和空载磁场中气隙磁密切向和径向分量表达式中的各次谐波系数,由式(33)~式(36)可得。
电磁转矩谐波总畸变率THDT如式(41),以此表征式(40)中电磁转矩波动的含量。
(41)
4 计算结果和优化设计
4.1 解析模型验证
用时步有限元软件,对表1参数电机进行仿真,有限元和解析模型的结果对比如图4所示。

(a)

(b) 图4 有限元法与解析法计算结果对比(a)永磁体涡流损耗 (b)电磁转矩Figure 4. Comparison of calculation results between FEA and analytic model(a)Eddy current loss of PMs (b)Electromagnetic torque
图4中,永磁体平均涡流损耗Pave有限元数值解为2 139 W,解析解为2 103 W,误差为1.7%;平均电磁转矩Tave有限元数值解为594.3 N·m,解析解为583.3 N·m,误差为1.9%。解析模型满足一定的精度要求。
4.2 电机尺寸影响分析
本文分析了定子绕组节距αy和永磁体极弧系数αp对涡流损耗和电磁转矩的影响。定子绕组节距αy的取值范围为[12°,48°],永磁体极弧系数αp的取值范围为[0.5,1]。参数示意图如图5所示。

图5 绕组节距和极弧系数示意图Figure 5. Schematic diagram of winding pitch and pole arc coefficient
对于上述绕组节距αy和极弧系数αp,使用解析模型,分别计算永磁体平均涡流损耗Pave、平均电磁转矩Tave和电磁转矩波动THDT的响应面,如图6所示。

(a)

(b)

(c) 图6 各参数指标的响应面(a)永磁体平均涡流损耗 (b)平均电磁转矩 (c)电磁转矩谐波总畸变率Figure 6. Response surface of each parameter(a)Average eddy current loss of PMs (b)Average electromagnetic torque (c)Total harmonic distortion rate of electromagnetic torque
由图6可知,减小绕组节距或永磁体极弧系数可降低永磁体平均涡流损耗;绕组节距在25°左右时,平均电磁转矩最大,且随着永磁体极弧系数的增大而增大;电磁转矩波动在绕组节距超过44°时较大,其值超过10%。在绕组节距小于44°时,电磁转矩谐波畸变率分布较为复杂,总体在1%~10%间波动。
4.3 电机尺寸优化设计
为提高平均电磁转矩Tave、降低电磁转矩波动THDT和永磁体平均涡流损耗Pave,对表1电机进行优化分析。优化算法为PSO,优化变量为定子绕组节距αy和永磁体极弧系数αp。使用加权法将多目标函数转变为单目标函数,目标函数为
(42)
式中,f为简化后的单目标函数,其值越小电机越理想;λ1、λ2和λ3分别是优化目标永磁体平均涡流损耗Pave、平均电磁转矩Tave和电磁转矩波动THDT的权值,依次取0.45、0.45和0.1;Pi=2 103 W,为优化前的永磁体平均涡流损耗;Ti=583.3 N·m,为优化前的平均电磁转矩;THDi=1.31%,为优化前的电磁转矩波动。
约束条件如式(43)所示。
(43)
PSO中,粒子数为20个,最大迭代数为200次,收敛曲线如图7所示。
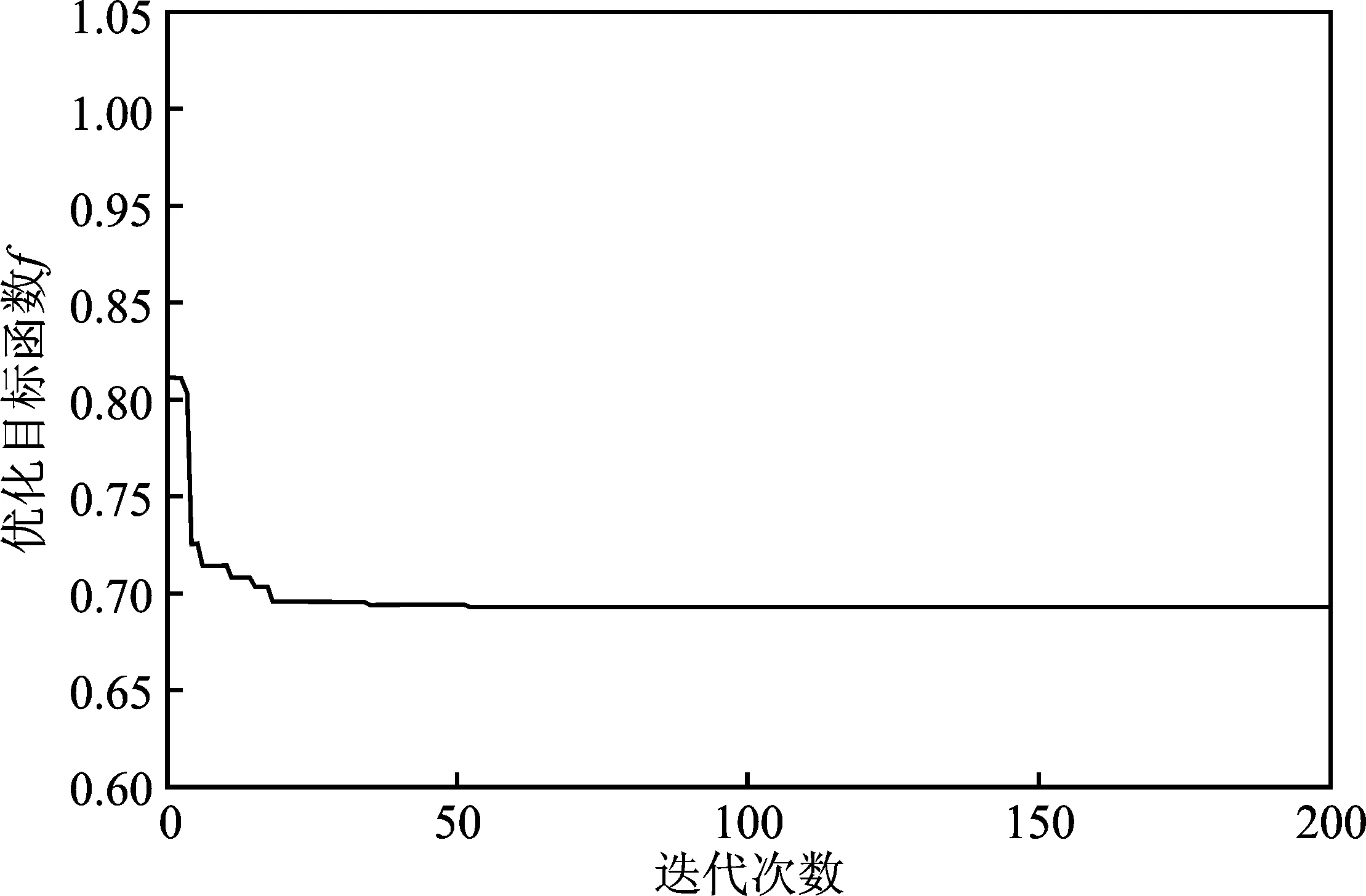
图7 粒子群算法收敛曲线Figure 7.Convergence curve of PSO
由图7可知,在前30次迭代中,最优粒子更新较快,在迭代后期,曲线趋于平稳,可认为在最优解附近。
经PSO计算可知,当绕组节距αy=20.6°且极弧系数αp=0.57时,最优目标f=0.69。此时平均涡流损耗Pave为514 W,降低了76%;平均电磁转矩Tave为454 N·m,降低了22%;电磁转矩波动THDT为0.42%,降低了68%,电机较为理想。
以上优化方案大幅降低了永磁体的平均涡流损耗和电磁转矩波动,但也小幅降低了平均电磁转矩。若想提高平均电磁转矩,需通过调整合适的权值λ1、λ2和λ3进行优化求解。
5 结束语
本文提出了一种永磁同步电机优化设计方案,优化目标函数基于电枢反应磁场和空载磁场两种解析模型。电枢反应磁场计算永磁体平均涡流损耗,引入感应电流片,降低了模型复杂性,提高了计算效率。解析模型均使用时步有限元进行精度验证。针对平均电磁转矩和平均涡流损耗,对定子绕组节距和永磁体极弧系数作参数影响分析。结果显示,两个参数在一定范围内有相似的相关性,此时难以确定理想的电机方案。使用权值将多目标函数简化为单目标函数,进行电机的优化设计。相比有限元模型,解析模型在优化迭代时效率更快,能快速收敛,得出给定权值下的最优电机设计。通过调整权值,可得到不同指标倾向的设计方案。
本文忽略了定子齿槽带来的空载涡流损耗和齿槽转矩,优化分析的输入参数也仅有两个。后续研究可以对解析模型进行修改,也可以增加优化算法的参数维度,或调整构建目标函数。
