柔性接入微电网的小信号建模

卢红文，袁旭峰，陈瑞洁，李雨龙

(贵州大学 电气工程学院，贵州 贵阳 550025)

为了促进分布式电源(Distributed Generatin，DG)大规模接入，使其得到更合理的利用，微电网技术成为近年来的重要研究热点[1]。微电网的提出，不但可以更充分地利用分布式电源，还能解决一系列由于大规模DG接入导致的问题，是传统电网向智能电网的重要过渡[2]。

为了更好地分析微电网运行的动态特性，对其进行小信号建模是十分有必要的[3]。通过对所建立的小信号模型进行特征值分析，不仅可以分析不同参数变化对微电网小信号模型稳定性的影响，还能够确定控制器的参数，提高系统的动态性能。

文献[5～7]在孤岛模式下建立了微电网主要子模块的小信号模型。文献[5]通过特征值分析，对控制策略进行改进，一定程度上提高了系统的稳定性。文献[6]基于特征值根轨迹对系统各参数进行优化，并对比了参数优化前后系统状态矩阵特征值的分布情况。文献[7]利用特征值分析，忽略一些对系统影响较小参数，并在此基础上提出了两种降阶模型，降低了微网小信号模型的复杂性。以上文献对微电网进行小信号建模时，推导的小信号模型受限于DG的数量，若DG数量发生改变，则需重新推导小信号模型，适用性不强，因此需要建立一种含N个DG的微网小信号模型框架。此外，上述研究仅对孤岛模式下的微电网进行了稳定性分析，只考虑了微网内部的影响，未考虑并网运行时外部对其产生的影响。与配网连接进行并网运行时同样存在一系列稳定性问题，若处理不好，严重时甚至会影响配网稳定性[8]。传统的并网运行方式是通过公共连接点(Point of Common Coupling，PCC)硬开关将微电网接入配电网，其无法对配网功率进行有效控制，难以对潮流进行柔性调节。文献[11]介绍了背靠背变流器(Back-To-Back Converter，BTBC)用于微网并网时的优势。文献[12]利用背靠背变流器作为互联开关，提升了系统稳定性，但该研究没有对系统进行全面的小信号建模，无法对该方式下的系统进行稳定性分析，也无法了解各种控制器参数对系统的影响。

在以上问题的基础上，本文利用BTBC取代传统PCC硬开关，对配电网与微电网进行柔性互联，提高微电网并网运行的动态特性。主要工作如下：首先分别建立了BTBC和含N个DG的微网数学模型，并将二者结合线性化，获得完整的微电网柔性并网运行小信号模型；随后利用MATLAB对其进行特征值分析，绘制出不同参数改变时所对应的根轨迹图，分析影响系统稳定性的关键参数；最后在PSCAD/EMTDC平台上搭建出基于下垂控制的微电网柔性并网运行模型，结合建立的小信号模型，通过不同工况下的仿真，验证了建模、分析与结论的正确性。

1 基于柔性互联接入的微电网

如图1所示，利用BTBC代替传统PCC硬开关，将微电网柔性接入配电网。电压等级为380 V，频率50 Hz。BTBC由配网侧VSC1、微网侧VSC2组成。

微电网内的DG采用下垂控制策略，既能在无通信的条件下保证系统的稳定运行，又能降低控制系统的复杂程度，具有一定的经济性[13]。BTBC配网侧VSC1采用定有功功率控制和定无功功率控制策略，微网侧VSC2为定直流电压和定无功功率控制策略[14]。

图1 基于柔性互联接入的微电网Figure 1. Microgrid based on flexible interconnection

2 基于柔性互联接入的微电网小信号模型

本节将推导如图1所示含N个DG的微电网小信号模型和BTBC小信号模型，并将其结合，获得系统完整的小信号模型。需要注意的是，本文的研究场景是柔性接入配电网的微电网，由于配网强度较高，且频率稳定，因此锁相环对系统的小扰动影响较小[15]。为精简模型，可忽略对锁相环的建模。

2.1 微电网小信号模型

2.1.1 DG并网逆变器

功率控制器控制框图如图2所示，有功、无功功率由测得的输出电压、电流计算而得。经低通滤波器滤除谐波，可提高功率波形质量。其中，ωc是低通滤波器的截止频率，s是拉普拉斯变换因子，mp为有功下垂系数，nq为无功下垂系数，ωn是微电网的额定角频率，Uo是微电网的额定电压。

图2 功率控制器控制框图Figure 2. Block diagram of power controller

功率控制器的小信号模型如式(1)、式(2)所示

(1)

(2)

其中，ωcom是公共DQ轴的角频率，通常取自第1个逆变器；Ap、Bp、Cp、Dpω、Dpu为系数矩阵。

双环控制器的框图如图3所示。

图3 双环控制框图Figure 3. Block diagram of double loop control

电压外环控制器小信号模型为

(3)

(4)

同理可得电流内环控制器小信号模型。

(5)

(6)

滤波电感电流为il，输出电压uo和输出电流io需满足

(7)

(8)

(9)

联立式(7)～式(9)并对其线性化，则输出滤波器及线路的小信号模型如式(10)所示。

(10)

利用下式将上述小信号模型统一转换到公共DQ参考坐标系下。

(11)

(12)

综上，第N个逆变电源的小信号模型如式(13)所示。

(13)

其中，ΔXinvN=[ΔθNΔPNΔQNΔΦdqNΔYdqNΔildqNΔuodqNΔiodqN]。

推导出含N个逆变电源并联系统的小信号状态空间模型，如式(14)所示。

(14)

2.1.2 负荷

负荷电流iload满足

(15)

经线性化得其小信号模型为式(16)。

(16)

2.2 BTBC小信号模型

从配网侧的VSC1、微网侧的VSC2和直流侧稳压电容进行独立建模。

2.2.1 配网侧VSC1

VSC1的内外环控制器框图如图4所示，小信号状态空间模型为

图4 VSC1控制框图Figure 4. Block diagram of VSC1 control

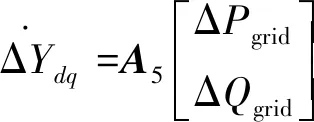
(17)

(18)

(19)

(20)

VSC1交流侧数学模型为

(21)

有功、无功功率的小信号模型为式(22)。

(22)

2.2.2 微网侧VSC2

图5 VSC2控制框图Figure 5. Block diagram of VSC2 control

VSC2的控制器框图如图5所示，微网侧内外环控制器小信号模型为

(23)

(24)

(25)

直流电压、无功功率小信号模型为式(26)。

(26)

2.2.3 完整的BTBC小信号模型

BTBC直流侧稳压电容满足式(27)，功率传输满足式(28)。

(27)

(28)

对式(27)、式(28)线性化，联立VSC1、VSC2的小信号模型，则BTBC的小信号模型为

(29)

其中，ΔN=[ΔPgridΔQgridΔudcΔQΔMdqΔYdqΔZdqΔis1dqΔis2dq]T。

系数矩阵As是一个十六阶的矩阵，矩阵中的0是二阶零矩阵。

2.3 基于柔性互联接入的微电网小信号模型

通过微电网交流母线电压这个中间变量，将微电网与BTBC的小信号模型结合，获得完整的微电网柔性并网运行小信号模型。为减少系统动态稳定性的影响，需在微电网交流母线和地面之间假定有足够大的虚拟电阻RN[16-18]。微电网交流母线电压小信号模型为

ΔuCDQ=RNMinvΔioDQ+RNMloadΔiloadDQ+RNMs2Δis2DQ

(30)

含N个DG的微电网柔性并网运行完整小信号模型为

(31)

其中，ΔXinv=[ΔXinv1ΔXinv2…ΔXinvN]T。此模型能根据微网内DG的数量进行相应变换，适用性较强，文中取N=2。

3 参数稳定性分析

利用MATLAB对上一节中建立的小信号状态空间模型进行特征值分析，绘制出不同参数变化时对应的根轨迹图，确定影响系统稳定性的关键参数。

分别改动有功下垂系数mp和无功下垂系数nq，变化范围为[1×10-5， 1×10-1]。如图6所示，增大mp或nq，系统的特征值会向虚轴靠近，系统阻尼减小，导致系统运行稳定性变差；当mp=1×10-3且nq=1×10-2时，系统处于临界稳定状态，若继续增大，将导致系统特征值实部为正，整个系统会失去稳定运行，出现发散振荡。另一方面，改变BTBC双环控制中PI调节器比例和积分参数。如图7(a)、图7(b)所示，Kpu和K的变化对特征值有较大的影响，最优取值范围分别为[1，23.2]、[0，0.9]。

关于微电网内部的参数稳定性分析，文献[4，6，7，15]已对其做了相关研究。由于本文系统的控制参数较多，篇幅有限，无法给出所有的参数分析。本文旨在对接入背靠背变流器后，对系统影响较大的参数进行分析验证，其余参数的分析可参考以上文献，本文不再赘述。

在已有文献所得结论的基础上，结合本文实验所得的根轨迹图，可知经背靠背变流器并网运行时mp、nq、Kpu、K这4个参数对微电网稳定性和动态性能影响较大。

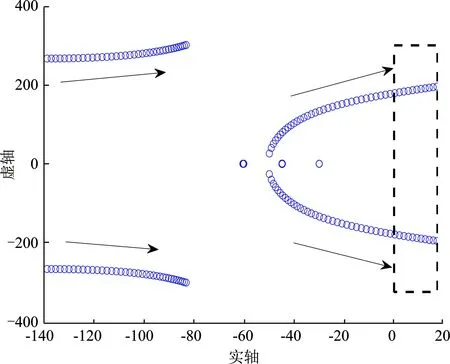
(a)

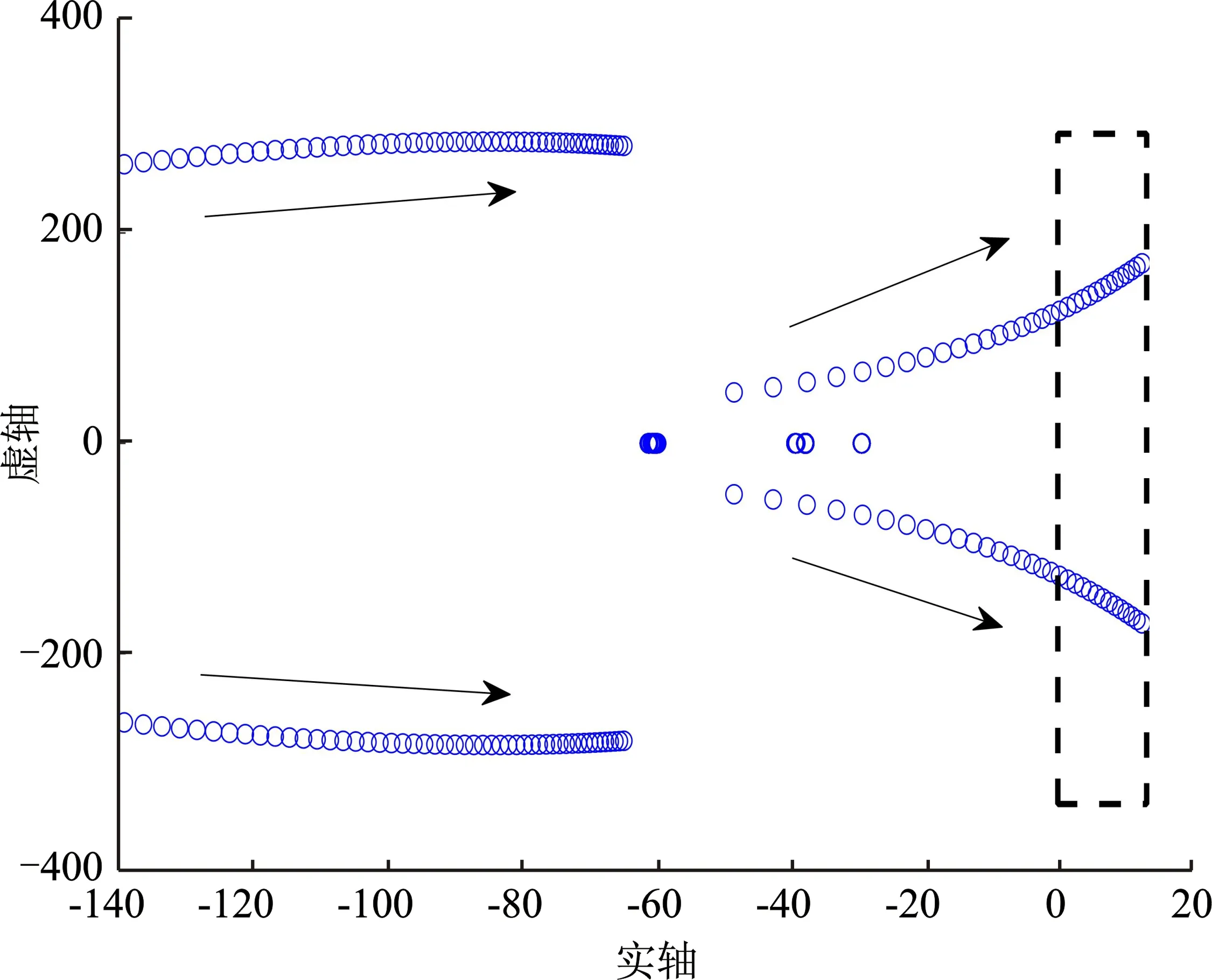
(b) 图6 有功、无功下垂系数变化时的根轨迹(a)mp∈[1×10-5， 1×10-1] (b)nq∈[1×10-5， 1×10-1]Figure 6. Root locus when droop coefficient of active and reactive power changes(a)mp∈[1×10-5， 1×10-1] (b)nq∈[1×10-5， 1×10-1]

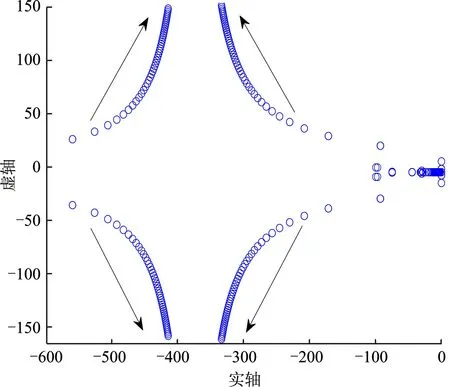
(a)

(b) 图7 PI参数变化时的根轨迹(a)Kpu∈[0，50] (b)K∈[0，50]Figure 7. Root locus when PI parameters change(a)Kpu∈[0，50] (b)K∈[0，50]

4 仿真验证与分析

本节在PSCAD/EMTDC平台上搭建出如图1所示的基于柔性互联接入的微电网电磁暂态模型。本文设置微网内分布式电源数量为两台，从多个工况下进行仿真验证。

4.1 改变有功、无功下垂系数

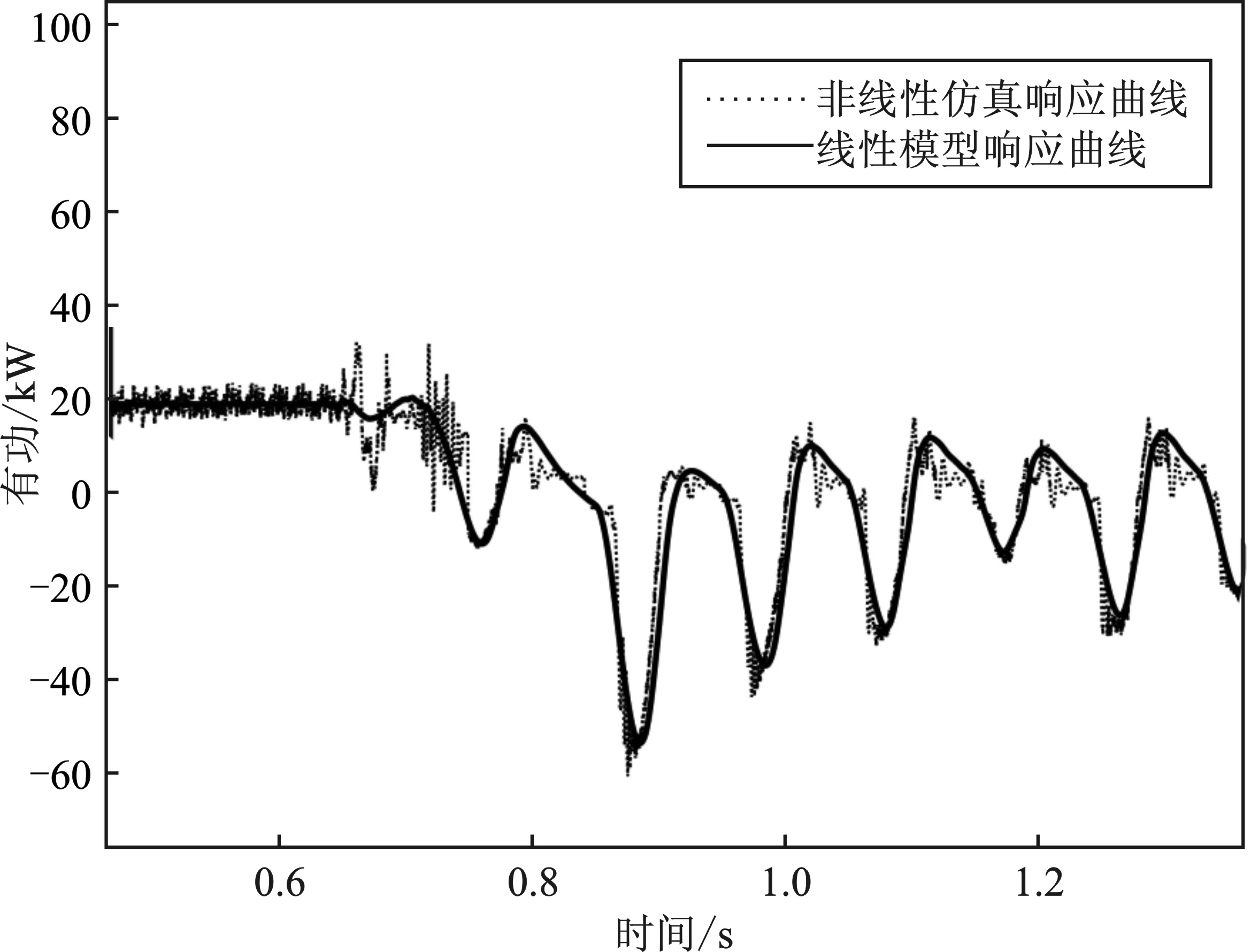
分别将mp和nq从1×10-5增大至1×10-1，仿真结果如图8所示。在0.6 s前，分布式电源发出的有功功率为20 kW，无功功率为5 kVar，BTBC输出的有功功率为50 kW、无功功率为0 kW，系统保持稳定运行。在0.6 s时，将mp或nq增大至1×10-1会导致系统内有功功率和无功功率出现大幅度振荡，使得系统无法稳定运行。非线性仿真响应曲线与线性模型响应曲线的吻合度较好，验证了建模、分析与结论的正确性。

(a)

(b)

(c)

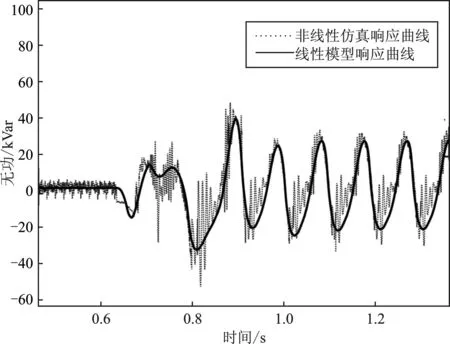
(d)图8 有功、无功下垂系数增大时的仿真波形(a)BTBC有功输出 (b)BTBC无功输出 (c)微电网有功输出 (d)微电网无功输出Figure 8. Simulation waveform when the droop coefficientof active and reactive power increases(a)Active output of BTBC (b)Reactive output of BTBC (c)Active output of microgrid (d)Reactive output of microgrid

4.2 负荷投切

微电网在并网运行的条件下，在1 s前只向负荷Load1(70 kW，10 kVar)供电，在1 s时投入Load2(20 kW，4 kVar)，在1.5 s时投入Load3(20 kW，0 kVar)，在2 s时断开Load2和Load3。图9给出了BTBC和DG的有功、无功出力情况，由于DG1和DG2容量设置相同，其响应曲线基本一致，这里给出其中一台DG的响应曲线即可。并网运行时微网交流母线的电压响应曲线如图10所示。

(a)

(b)图9改变负载时的功率输出(a)并网运行时有功功率响应曲线(b)并网运行时无功功率响应曲线 Figure 9. Power output when changing the load(a)Active power response curve during grid connected operation (b)Reactive power response curve during grid connected operation

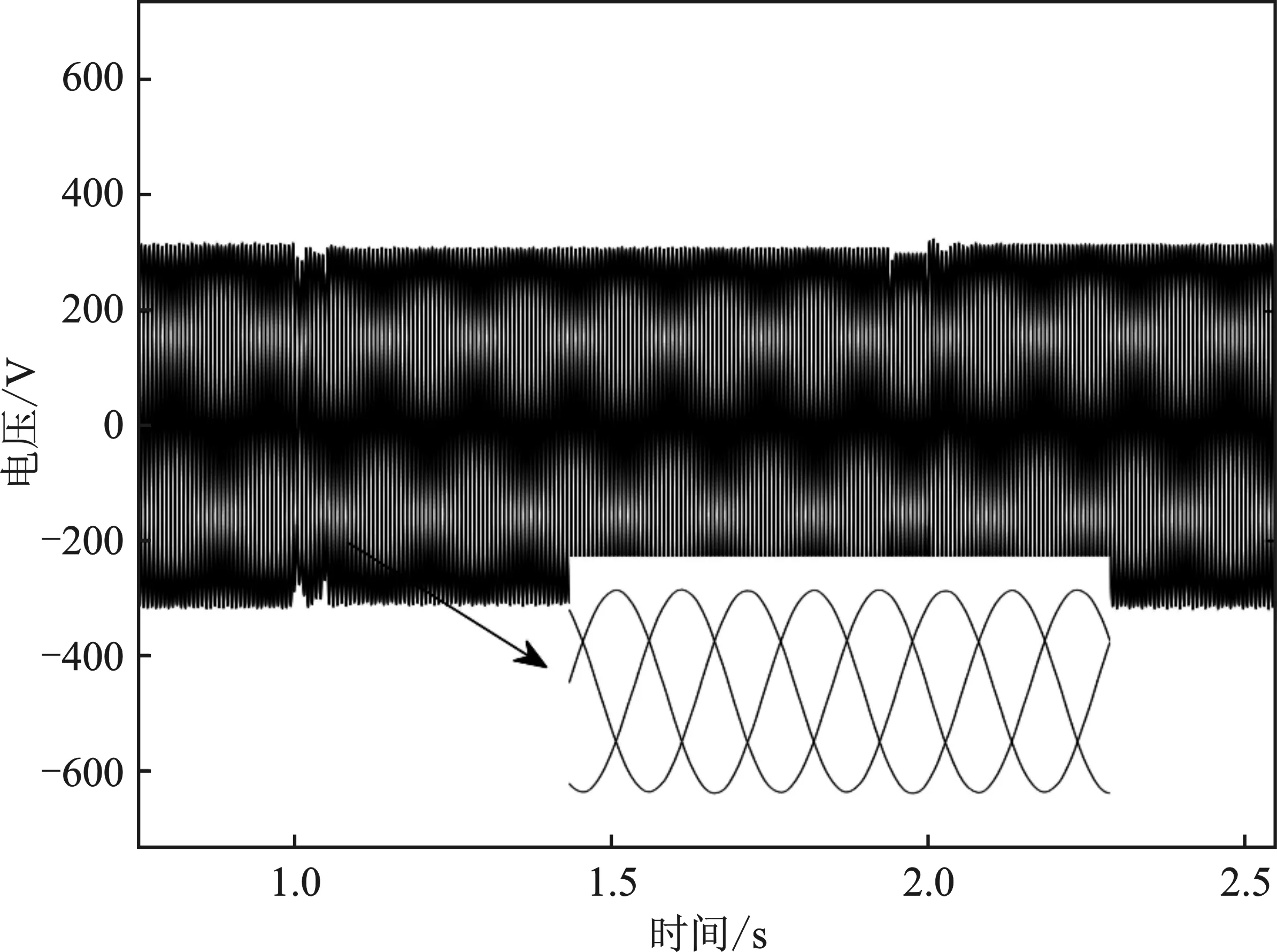
图10 并网运行时电压响应曲线Figure 10. Voltage response curve during grid connected operation

在1 s之前，BTBC的有功输出为30 kW，无功输出为0 kVar，两台分布式电源的有功输出都为10 kW，无功输出都为5 kVar。在1 s时投入Load2，DG1和DG2的无功输出都增加至7 kVar、有功输出增加至30 kW。此时分布式电源的有功输出已达到最大值，因此在1.5 s时投入Load3后，通过BTBC主动调节注入微电网的功率，将有功输出增加至50 kW。在2 s时断开Load2和Load3，BTBC有功输出恢复至30 kW，DG1和DG2的有功输出恢复至20 kW。整个运行过程中，利用BTBC主动调节潮流的优良特性能合理调节配网输出功率，保证系统的稳定运行。在负荷投切时，微网交流母线电压只有很小的一段瞬时波动，其余时段的电压和频率均保持稳定，且电压波形质量较好。

4.3 故障隔离

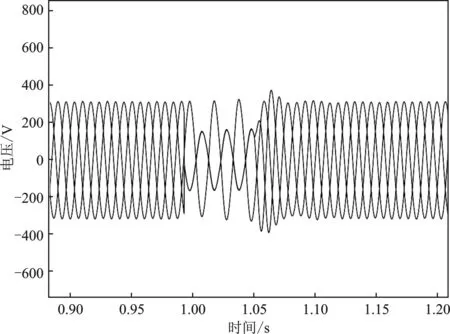
微电网在并网运行的条件下，在1 s时在微网侧分别设置瞬时单相短路故障、两相短路故障、三相短路故障。图11展现出了在这3种故障情况下微网侧与配网侧的电压响应曲线。以上任意一种故障发生时，都会影响到微网侧的交流母线电压，而配网侧的电压不受影响，这是由于BTBC的存在将微网隔离于配网，在保持它们之间功率流动的同时，还能起到故障隔离的作用。

(a)

(b)

(c)

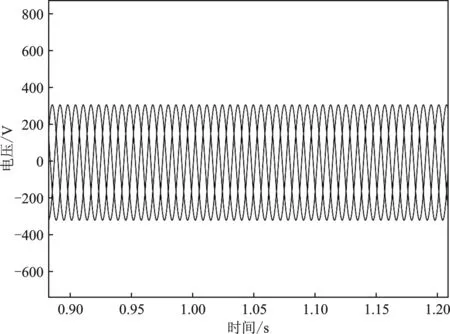
(d)图11 故障时的电压响应曲线图(a)单相短路故障时微网侧电压响应曲线 (b)两相短路故障时微网侧电压响应曲线 (c)三相短路故障时微网侧电压响应曲线 (d)配网侧电压响应曲线 Figure 11. Voltage response curve during fault(a)Voltage response curve of microgrid side under single-phase short-circuit fault(b)Voltage response curve of microgrid side under two-phase short circuit fault (c)Voltage response curve of microgrid side in case of three-phase short circuit fault(d)Distribution network side voltage response curve

5 结束语

文中利用BTBC取代传统PCC硬开关，实现了配网与微网的柔性互联。对BTBC和含N个DG的微网进行数学建模，将二者结合并线性化后得到完整的基于柔性互联接入的微电网小信号状态空间模型，此模型能根据微网内DG的数量进行相应变换，不需要重新推导，适用性较强。利用此模型，可以对系统内的各种控制参数进行特征值分析，结合搭建的仿真模型，研究结论如下：

(1)利用BTBC对配电网与微电网进行柔性互联，能将微网隔离于公用电网，同时保持它们之间的功率流动，便于微电网和公用电网之间的功率主动控制，也便于主网与微电网的协同控制，提升稳定性能；

(2)确定了影响微电网稳定性和动态性能的关键参数主要是mp、nq、Kpu、K这4个因素。Kpu和K的最优取值范围分别为[1，23.2]和[0，0.9]。当mp=1×10-3且nq=1×10-2时，系统处于临界稳定状态；当mp>1×10-3且nq>1×10-2时系统会失去稳定运行，出现发散振荡。

在今后的研究中将进一步优化控制参数，改进控制策略，提高模型的性能。