基于蚁群算法的无人船平滑路径规划

孙鹏娜，张忠民

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

无人驾驶船(Unmanned Surface Vehicles，USV)与传统人工驾驶船舶相比，具有高速化、智能化以及模块化等优点[1]。无人船可以代替人工驾驶船舶执行某些特殊危险的任务，降低了人力成本。其还能够长时间航行，有效规避疲劳驾驶的风险等优点，因此具有良好的军事及经济价值[2]。在复杂多变的水面环境中，为了保证无人船能够安全航行，规划一条路径较短、路线平滑、安全度高的航行路径至关重要[3-4]。在智能启发式算法中，蚁群算法更为稳定、可靠，故被广泛应用于寻找最优解。但该算法也存在收敛性差、搜索盲目、易收敛到次优解等问题。近些年，国内外对蚁群算法进行改进优化并应用于路径规划中，取得了一定的成果。文献[5]提出了一种融合粒子群和蚁群算法的路径规划算法，有效提高了初期寻径和全局搜索能力，减少了收敛迭代次数并缩短搜索使用时间。文献[6]提出基于路程因素、路平滑因素及高度平缓因素的启发函数和信息素更新机制，改进算法具有较好的全局搜索能力及收敛性。文献[7]采用初始信息素不均匀分配、引入权重因子和改进蚁群信息更新规则，规划出平滑的全局路径。文献[8]为提高蚁群算法的动态避障能力，提出了一种基于模糊逻辑和蚁群算法的路径规划策略，搜索路径较短，获得了较好的效果。文献[9]在启发函数和信息素更新机制中融合A*算法和狼群分配原则，改进的蚁群算法具有较好的收敛性和可靠性。

结合近些年蚁群算法的改进方法和蚁群算法在规划路径时存在的问题，本文进行了以下改进：提出了基于路径总长度、路径转弯次数以及自适应距离因子的改进启发函数；结合路径平滑性因素和自适应更新策略的信息素的更新标准，引入了障碍物因子的路径转移概率，并对输出的最优路径进行平滑处理，从而提高路径搜索能力、增加算法的收敛性和路径的安全性。

1 传统蚁群算法原理

蚂蚁根据启发函数的引导、路径上的信息素浓度强弱以及当前节点状态的转移概率大小来实现路径的搜索[10-11]。

1.1 转移概率的选择

当蚂蚁k位于当前栅格i选择下一步行进方向时，会根据当前各条路径上的信息素浓度τi，j(t)及启发函数ηi，j(t)来决定下一步路径，路径转移概率为

(1)

式中，α表征信息素重要程度，其值与算法的全局搜索能力有关；β表示启发函数重要程度，其值的大小影响蚂蚁选择下一步相邻栅格；allowedi表示蚂蚁k可选择的下一步可行栅格集合。ηi，j(t)通常与两栅格中心的欧氏距离成反比。栅格i、j的距离d越小，则选该路径的启发函数就越大。

(2)

1.2 信息素更新方式

蚂蚁在行进过程中会留下信息素，用来为其他蚂蚁提供指向信息。在蚁群的正反馈机制下，路径上的信息素浓度强弱与吸引蚂蚁数量成正比[12]。

目前蚁群算法中常用的信息素更新机制为蚁周模型，且信息素的分布只于路径长度有关，更新方式如下

τi，j(t+1)=(1-ρ)τi，j(t)+ρΔτi，j(t，t+1)

(3)

(4)

通常设置初始信息素为

τi，j(0)=C

(5)

式中，ρ是信息素挥发系数，一般取ρ<1；Q是信息素常数；Lk为蚂蚁k在本次迭代中走过的路径长度；C为常数。下文在此基础上改进信息素更新方式。

2 改进蚁群路径规划算法

2.1 改进启发函数和转移概率

由式(2)可以看出，传统蚁群算法中启发式函数只与路径长度有关，而在实际的路径规划过程中，评价路径优劣不能只考虑与路径长度因素，路径的平滑程度、自适应距离启发因子、算法运行时间等都是路径的评价标准。因此本文从路径总长度、路径的平滑程度、自适应距离启发因子等方面对启发函数进行改进，改进方法如式(6)所示。

ηi，j(t)=r(i，j，g)+φi，j(t)

(6)

2.1.1 路径长度因素

传统蚁群算法的启发函数与当前栅格到待走栅格之间的距离有关，本文提出的路径长度因素与待走栅格到目标栅格以及待走栅格到起始栅格之间的距离因子有关。引入距离函数r(i，j，g)，其定义如下

(7)

(8)

dmax=max{d[m，g]}

(9)

dmin=min{d[m，g]}

(10)

m=1，2，…，card(allowedi)

(11)

式中，dmax、dmin是当前蚂蚁k下一步可选择的所有栅格中心到目标栅格中心的最大、最小距离；μ(s，j，g)表示表示待走栅格j的中心到起始栅格和目标栅格中心的距离启发因子；a、b是距离系数；δ是距离启发信息系数；d(s，j)和d(j，g)分别表示下一个可行栅格j到起始栅格和目标栅格中心的欧氏距离。

2.1.2 路径平滑度因素

考虑到无人船的实际行驶情况，当规划路径转弯次数尽可能少，转弯角度也尽可能小[13]，且路径更加平滑时，可提高路径行驶的安全性。因此，本文引入平滑性启发函数，如式(12)所示。

(12)

式中，δ为路径平滑系数；η是表征直行重要程度的系数；Dv，j(t)表示蚂蚁上一步行走的转向方向；Di，j(t)表示下一步待走的转向方向。如果当前转向与上次转向相同，即当前路径为直线行走时，平滑性启发函数大，从而指引蚂蚁沿直线行走，减少了不必要的路径转弯次数。

2.2 改进转移概率

传统算法中的路径转移概率只考虑了待走栅格与目标栅格之间的距离启发因子，忽略了待走栅格与障碍栅格之间的距离启发信息。因此本文在转移概率中引入了障碍物启发函数，改进后的路径转移概率为

(13)

γj，b(t)=1/mind(j，b)，b=1，2，…，card(obsj)

(14)

式中，γj，b(t)表示待走栅格j到邻接障碍栅格b的欧式距离最小值的倒数。

2.3 改进信息素更新方式

2.3.1 改进信息素更新模型

根据启发因子的改进思路，将路径长度和路径平滑度作为信息素的更新标准，改进方式如下

τi，j(t+1)=(1-ρ)τi，j(t)+ρΔτi，j(t，t+1)

(15)

(16)

Sk(t)=a×Lk(t)+b×Tk(t)

(17)

(18)

式中，Sk(t)为第t次迭代中蚂蚁行走路径的性能指标，Sk(t)越小，该路径的信息素分配越高，路径的综合性能越好；Lk(t)为当前迭代路径；Tk(t)为当前路径的转弯个数；Lbest为历史迭代中的最优路径；a、b为常系数；μ为信息素调节系数。

2.3.2 自适应信息素挥发系数

蚁群算法的正反馈特性会引导蚂蚁倾向于走某一较优解，减小了对全局的路径搜索，导致算法收敛到次优解[14]。减小ρ可以增强对路径的全局搜索但会降低收敛速度[15]。根据信息素挥发系数的性质，本文提出可以根据不同要求进行动态调节的信息素挥发系数ρ。本文提出的改进为：

(1)设置信息素的上下限阈值，且t=0时，ρ=ρmax；

(2)设定迭代次数阈值M；

(3)当迭代次数Nc等于M后取常数ρ0。ρ0值可根据不同环境进行调节，当迭代次数Nc不等于阈值M时，信息素挥发系数ρ减小并与信息素阈值下限进行比较，取两者间较大值，即

(19)

式中，λ为递减常数，λ<1。

2.4 路径平滑处理

传统蚁群算法没有考虑路径转向时的转弯半径，而在实际行驶过程中，需要考虑转向能耗并且避免转向过程中发生侧翻。因此本文在改进蚁群算法规划航行路径的基础上，通过B样条插值法对路径进行平滑处理，从而确保船舶行驶的稳定性[16]。图1为简易无人船简化模型。

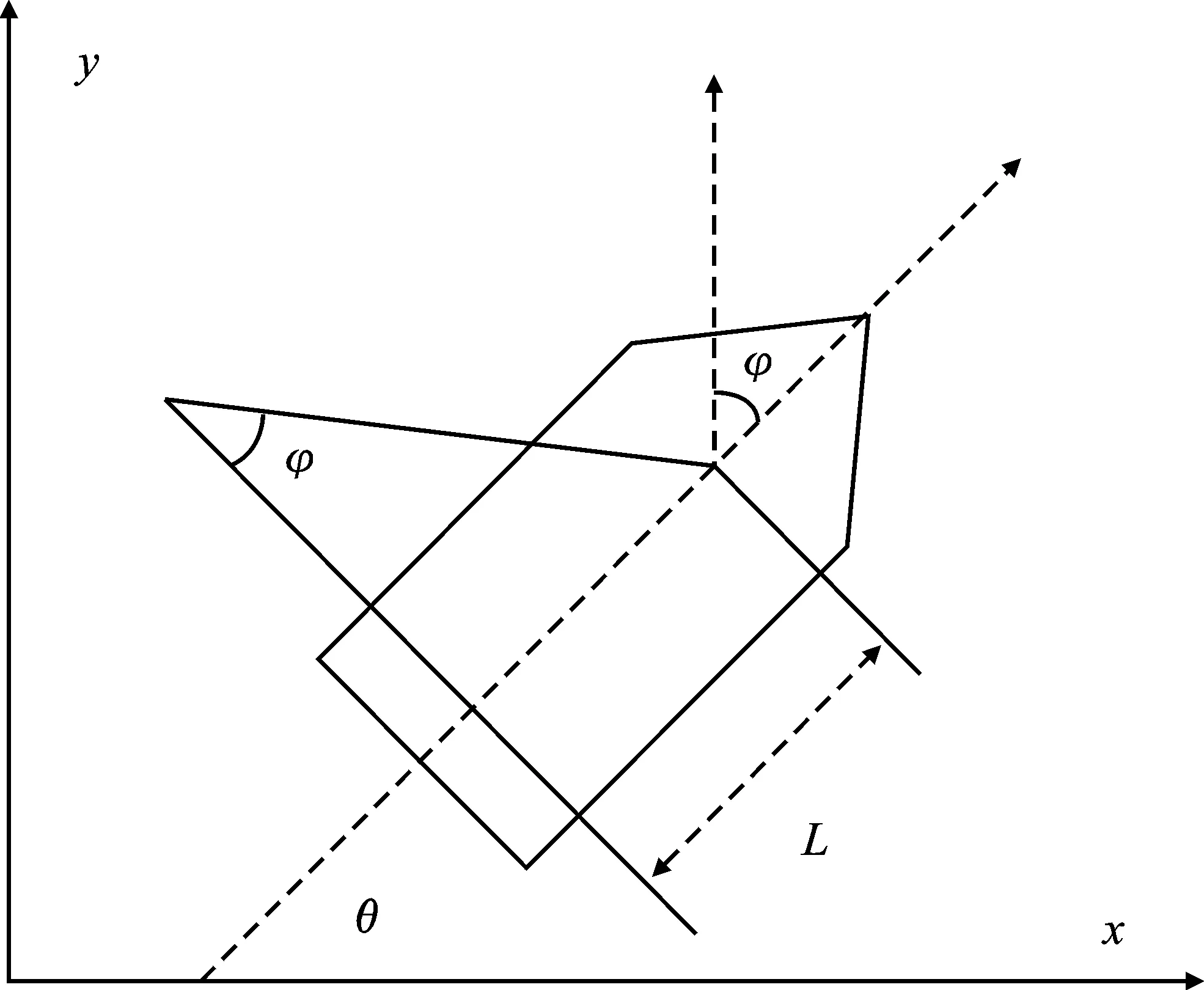
图1 无人船转向简化模型Figure 1. Simplified steering model of USV

假设无人船在航行过程中某一时刻处于(x，y)位置，此时无人船的航向为θ，船舶中轴与转向方向的偏移角为φ，无人船的转向角度具有机械特性的约束[17]，即

|φ|≤φmax

(20)

因此，无人船行驶的最小转弯路径为

Rmin=L×cotφmax

(21)

式中，L是船舶的中轴距离差。为保证转向的安全性，需要满足转弯路径大于最小转弯路径。

路径平滑处理中一般使用插值法进行路径拟合。常用的插值法有贝塞尔曲线、多项式曲线以及B样条曲线等。贝塞尔曲线插值容易，但改变某个关键点时整个曲线随之变化。多项式曲线在高次插值时可能会出现龙格现象[18]。B样条曲线是通过逼近关键点产生的，可以局部控制曲线，具有凸包性、保凸性、变差减小性等优点[19]。因此对输出的最优路径提取关键节点，对拐点进行B样条插值处理。

图2 平滑处理前后路径对比Figure 2. Comparison chart of path smoothing and unsmoothing

平滑处理结果如图2所示。未进行平滑处理时，路径拐点明显，某些转向角度达到了π/2，不符合实际航行需求。而平滑处理后的路径可以有效满足转向时安全转向角和最小转弯路径的要求。

2.5 改进算法流程

本文改进蚁群算法的运行流程如图3所示。

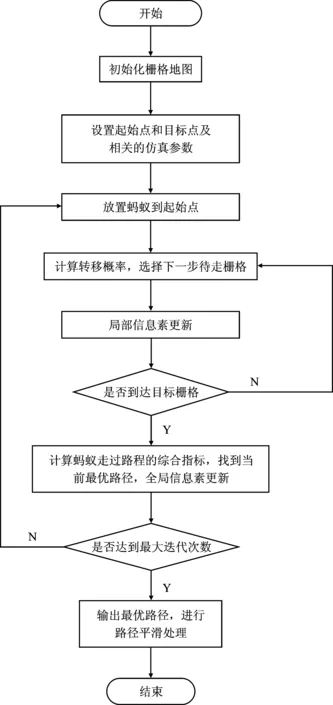
图3 改进算法运行流程Figure 3. Flow chart of the improved algorithm

3 算法仿真及分析

为了验证改进蚁群算法在路径规划中的可行性，本文使用MATLAB软件在不同栅格环境下进行仿真。

3.1 20×20栅格环境仿真

建立较为简单的20×20栅格环境，对本文改进的蚁群算法进行了仿真。设置对角线型的起始栅格与目标栅格，并对仿真参数进行设置。多次仿真后的结果如图4所示。

(a)

(b)

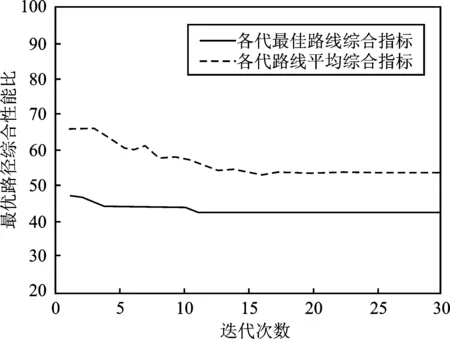
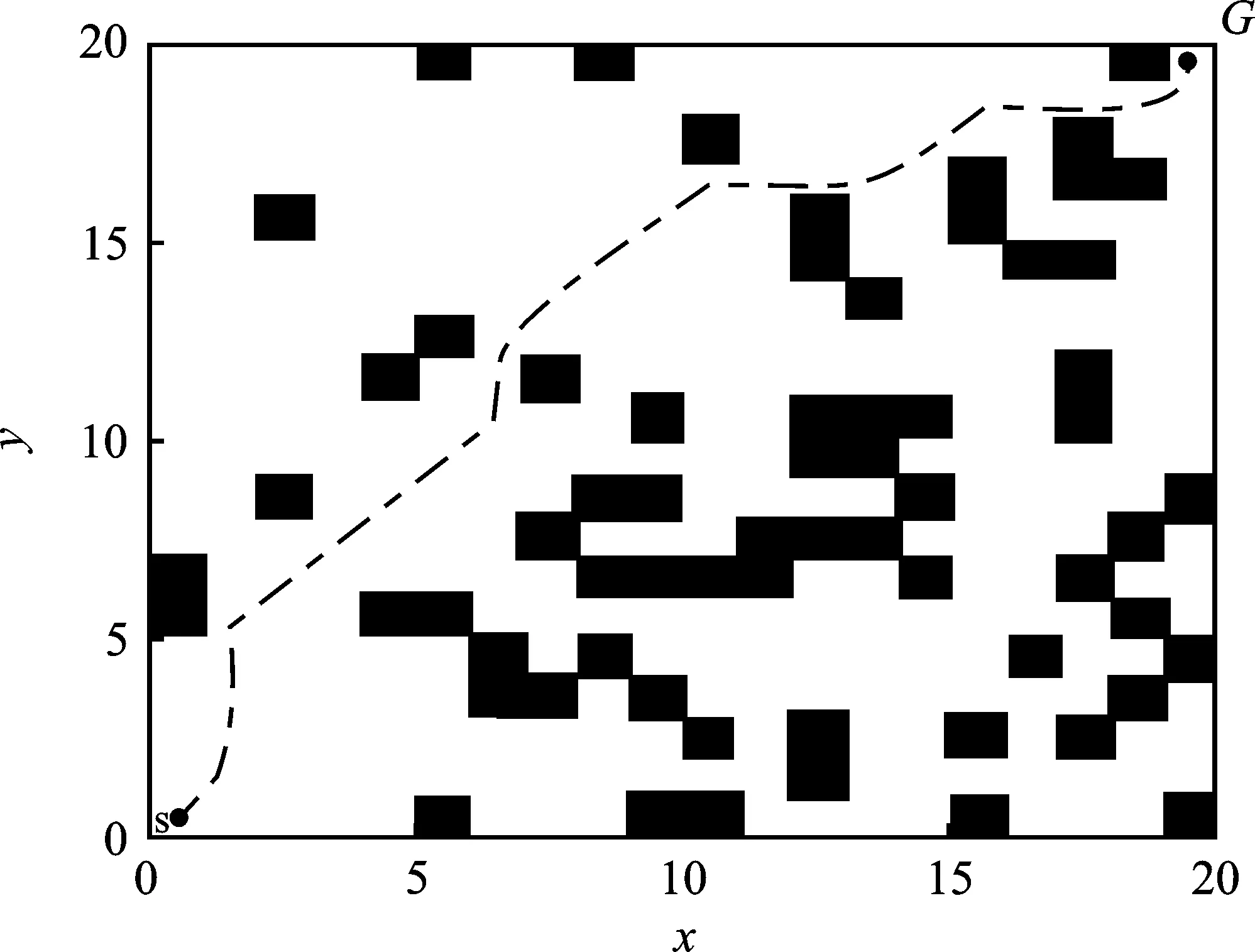
(c)图4 20×20栅格最优路径及路径平滑优化(a)改进算法最优路径仿真 (b)平滑处理后的路径 (c)路径综合性能及平均综合性能迭代Figure 4. Optimal path and path smoothing in 20×20 grid map(a)Optimal path simulation of improved algorithm (b)Optimal path simulation after path smoothing (c)Iterative graph of path comprehensive and average comprehensive performance

从图4(a)可以看到，为了有效避免与障碍物的边角相撞，保障路径的安全性，改进算法规划的路径牺牲了一部分路径长度并且增加了转弯个数，但是路径的可行性有明显提高，说明该改进算法能较好地对环境的进行全局路径规划。图4(b)为平滑处理后的路径，能够较好地处理拐点信息，转向角度更加符合无人船实际行驶情况。下文中改进算法仿真结果都为路径平滑处理后的路径。由图4(c)中可以看出该改进算法具有较好的收敛性，迭代曲线整体呈下降趋势并且收敛速度较快，算法后期的收敛性较为稳定，没有出现收敛到次优解和陷入局部最优解的情况。通过仿真分析可知，本文的算法改进较为符合预期结果。

3.2 30×30栅格环境仿真

为了验证本文改进蚁群算法在路径规划的可靠性，使用30×30栅格环境对本文改进蚁群算法、传统蚁群算法以及文献[6]提出的改进算法进行仿真。

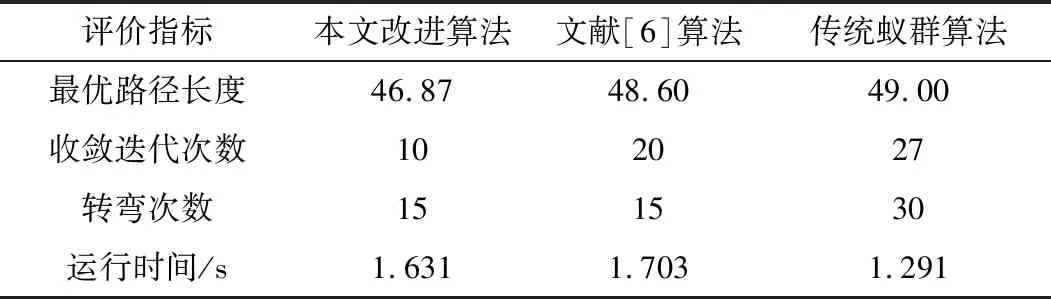
表1 30×30栅格环境下3种算法仿真结果

(a)

(b)

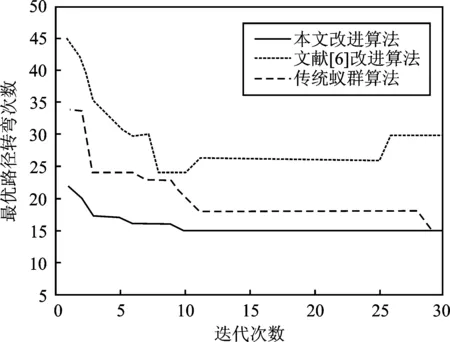
(c)图5 30×30栅格环境下3种算法仿真结果(a)3种算法最优路径对比图 (b)3种算法最优路径长度收敛图 (c)3种算法最优路径转弯次数收敛图Figure 5. Simulation results of three algorithms in 30×30 grid map(a)Optimal path comparison graph of three algorithms (b)Optimal path length convergence graph of three algorithms (c)Path steering times convergence graph of three algorithms

从图5可以看出，点线表示的传统蚁群算法历代路径收敛波动较大，迭代性能不够稳定，并且从图5(c)中可知传统算法在转弯次数达到最优之后，反而收敛到一条转弯次数较多的路径；点划线表示的文献[6]改进蚁群算法和实线表示的本文改进算法在路径长度和转弯次数的迭代曲线整体呈下降趋势。表1仿真结果显示，本文改进算法与传统蚁群算法、文献[6]算法相比，在迭代初期、各代最优路径以及最后输出的最优路径在收敛性、最优路径长以及转弯次数方面都具有明显优势，并且在第10次迭代左右就收敛到了最优结果，算法运行时间高于传统算法优于文献[6]的改进算法。

3.3 50×50栅格环境仿真

为了进一步验证本文改进算法具有较优的全局搜索性和较高的路径规划优化能力，设置了更为复杂的50×50的栅格环境进行仿真。由于在30×30栅格环境中，传统蚁群算法规划的路径在路径长度和转弯次数以及算法收敛性等方面都明显劣于文献[6]改进蚁群算法和本文改进蚁群算法，因此在50×50的栅格环境下只对本文改进算法和文献[6]改进算法进行仿真。

表2 50×50栅格环境下两种算法仿真结果比较

(a)

(b)

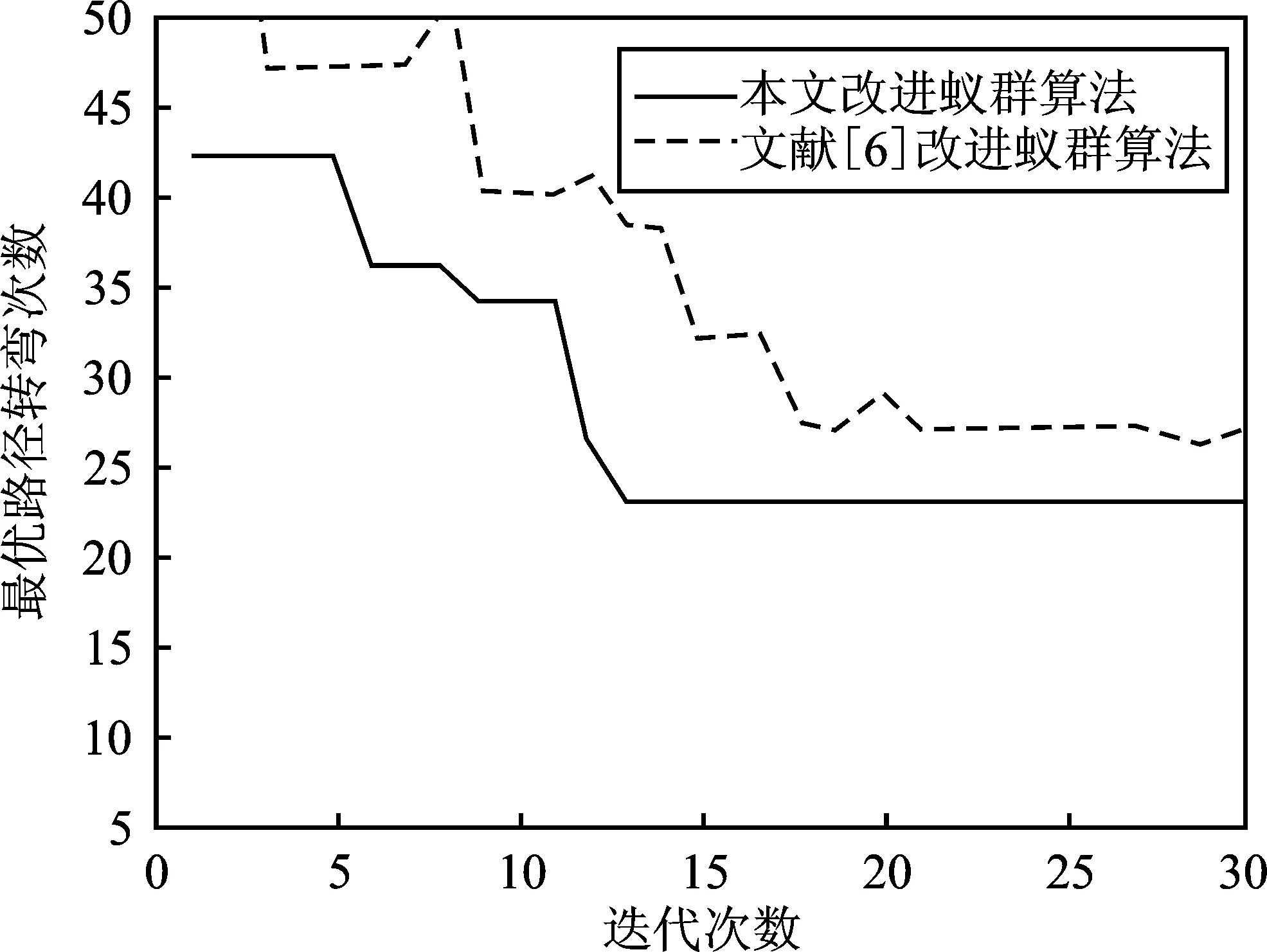
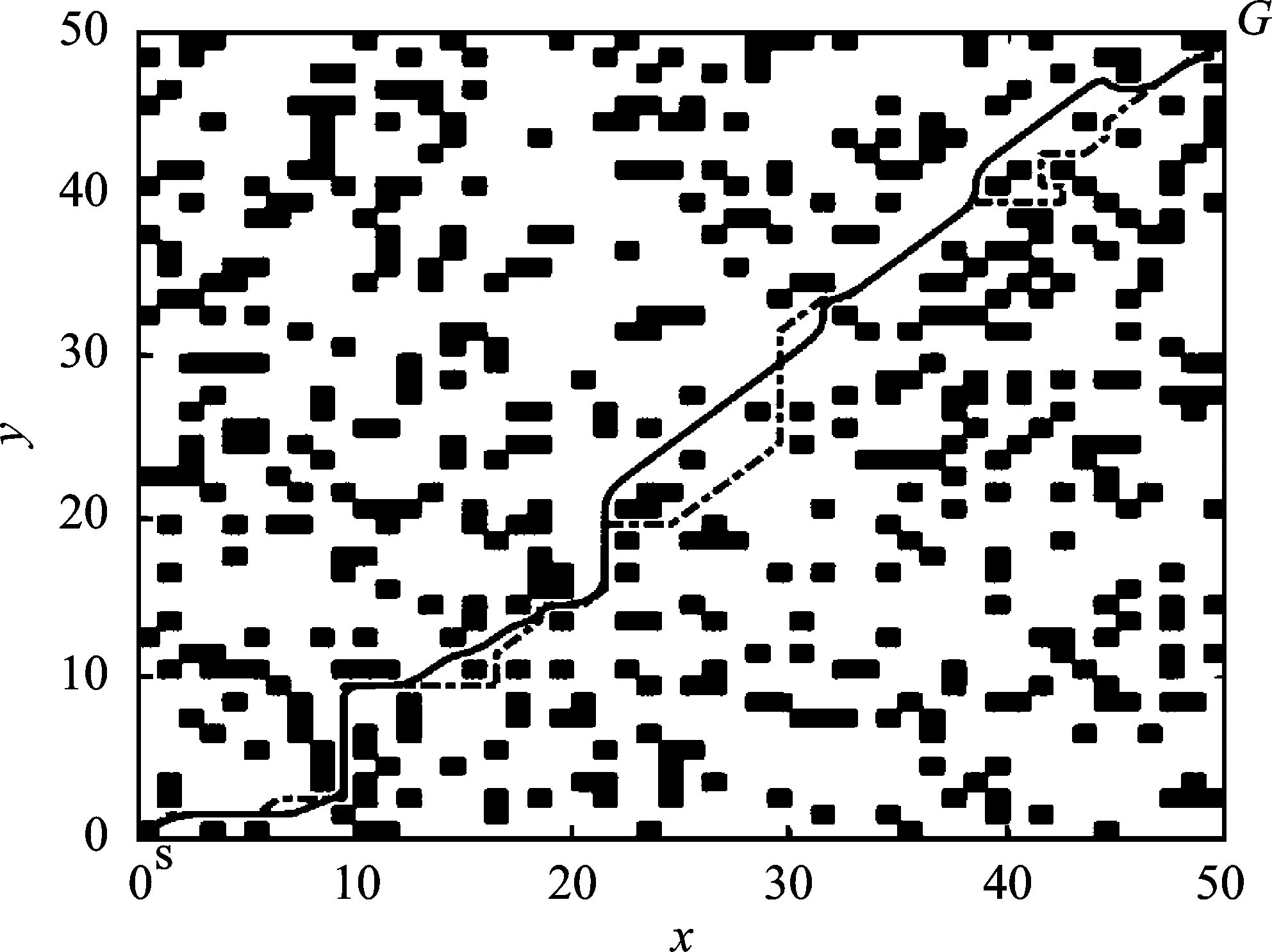
(c)图6 50×50栅格环境下两种算法仿真结果比较(a)两种算法最优路径对比图 (b)两种算法最优路径迭代收敛图 (c)两种算法最优路径转弯次数收敛图Figure 6. Simulation results of two algorithms in 50×50 grid map(a)Optimal path comparison graph of two algorithms (b)Optimal path length convergence graph of two algorithms (c)Path steering times convergence graph of two algorithms

如表2和图6所示，在较为复杂的仿真环境中，点划线表示的文献[6]算法迭代变得不够稳定，而实线表示的本文改进蚁群算法的迭代曲线整体呈下降趋势。迭代初期、各代最优路径以及最后输出的最优路径在收敛性、最优路径长以及转弯次数方面都具有明显优势，并且在第13次迭代后期收敛到了最优路径。本文改进算法后期的收敛性较稳定，且稳定性较好，没有出现收敛到次优解的情况。

4 结束语

本文针对无人驾驶船舶在航行环境复杂，传统算法不能满足路径长度、路径平滑度、路径安全等多方面的要求，根据无人船航行的特点和要求，对传统蚁群算法进行了优化改进，使之符合实际船舶的航行需求。本文在启发函数中加入了路程长度、平滑度等因素的影响，引入了障碍物对转移概率的影响并对信息素更新方式进行了改进，从而设计出一条各方面都较优的路径。根据仿真结果，本文改进的蚁群算法有效解决了传统蚁群算法存在的问题，规划的路径在航程、路径平滑度、安全性等方面都有较好的表现。