复合材料件单搭接胶接结构可靠性分析

韩子健，周金宇，庄百亮，倪伟

（1.江苏理工学院机械工程学院，江苏 常州 213001；2.金陵科技学院机电工程学院，江苏 南京 211169；3.机械科学研究总院江苏分院有限公司，江苏 常州 213001）

1 前言

在能源短缺、轻量化成为必然趋势的大环境下，复合材料得到广泛运用。为了更好的传递复合材料件之间的载荷，需要对复合材料件连接方式进行研究。复合材料的连接方式主要有两种：机械连接和胶接连接。机械连接需要在复合材料件上制孔，不仅会破坏复合材料的增强纤维的连续性，而且容易造成应力集中，降低连接效率。而胶接连接是通过胶粘剂把两个或多个构件连接起来，无开孔导致的应力集中的问题，而且具有零件数目少、结构轻、连接效率高、能获得光滑的气动外形等优点，因此胶接连接广泛运用于复合材料件的连接中。但是在复合材料件胶接连接时，存在诸多影响因素，在设计时需要考虑实际工程中的这些不确定因素。可靠性设计方法拥有常规的设计方法不可比拟的优势：可靠性设计具有明确的可靠度指标值；可靠性设计时考虑了各随机变量的离散性。因此可靠性分析在复合材料构件连接结构设计中显得尤为重要[1]。

目前国内外对胶接连接可靠性研究的学术关注度逐年增大，文献[2]针对复合材料胶接结构，从复合材料属性和胶接接头几何参数两个方面讨论了如何提高结构的承载力；文献[3]从解析法和数值法两个方面介绍和比较了目前常用的胶接接头强度预测方法，为复合材料胶接接头的可靠性分析提供基础理论指导。文献[4]针对金属被粘物的同轴胶接接头采用有限元分析得到胶层最大剪应力，与胶粘剂的剪切强度进行比较，通过可靠性算法得到同轴胶接接头的可靠度。文献[5]针对静态载荷下的斜搭接胶接结构，只考虑胶层失效，采用三维有限元分析获得极限状态函数，建立了可靠性分析概率模型。文献[6]针对碳纤维层合板与钢的双搭接胶接接头进行大量试验，并考虑组成材料的力学和几何不确定性，对结构进行可靠性分析，得到胶粘剂剪切强度是决定胶接结构可靠度指标最重要的材料性能。针对复合材料件胶接结构进行可靠性分析，基于复合材料弹性理论和载荷相关串联系统模型建立了胶接结构的可靠性功能函数，并采用Monte−Carlo法求取可靠度，该方法可为复合材料胶接结构的广泛应用奠定理论基础。

2 层合板强度分析

层合板为各向异性材料，假设由n个单层板组成，单层板厚度为ti(i=1，2，…，n)，层合板厚度为t。各单层板的铺层角度是可设计的。当层合板受到面内载荷N时，各单层板的承受能力不同，对层合板进行强度分析时，首先要得到各单层板的应力：

式中：σ11，σ22、τ12—单层板各方向上的主应力；Qi—二维刚度矩阵，可通过单层板弹性常数求得[7]；Qˉi—二维刚度矩阵的转换矩阵；Ti—第i层板的坐标转换矩阵；N—各层合板承受的载荷；a、b—加载比例系数；Ac—层合板拉伸刚度矩阵。

各失效单元的极限状态，可由Tsai−Hill失效准则给出，失效判据为：

式中：Xt、Yt—单层板纵向、横向拉伸强度；S—单层板剪切强度。

根据式（1）得：

将式（3）代入式（2），得由层合板失效单元抗力为：

式中：i=1，2，…，n。

3 胶层强度分析

胶接结构的使用的结构胶粘剂不同于一般的胶粘剂，它具有耐高温、高强度、高耐久性等特。主要分为韧性胶和脆性胶，脆性胶的剪切强度普遍大于韧性胶；韧性胶的剪应变极限大于脆性胶[8]。在胶接连接静剪切强度并不取决于某个特征参数，而是由剪切应变能决定的。因此以强度较高的韧性胶为胶层研究对象。通过弹性力学分析胶接接头的微元体受力情况，得到胶层剪应力的分布函数，再根据应力分布状态得到胶层失效单元的抗力。

3.1 层合板的等效模量

复合材料应用于航空、汽车等领域时，为了简便计算，常把复合材料层合板看作杆元结构，因此需要研究单层板的性能和铺层顺序对复合材料层合板的等效模量的影响，并求取等效模量。

求取层合板的等效模量时，需确定每层整体坐标的刚度矩阵

式中：—每层整体坐标柔度矩阵—应变之间的坐标转换矩阵；E1、E2、ν1、G—单层板基本参数。

假定单层板厚度为ti、层合板由n个单层板组成，层合板厚度为t，则有层合板轴向等效模量E：

3.2 胶层的弹性分析

单搭接接头模型，如图1所示。上下被粘物为等刚度层合板在单位宽度上受拉伸载荷N作用，复合材料层合板的厚度为t，胶层厚度为ta，搭接长度为L=2l，由式(10)得到复合材料层合板的等效弹性模量。

图1 拉伸载荷下的单搭接接头与微元体受力图Fig.1 A Single−Lap Joint Under Tensile Loading &Infinitesimal Stress Unit Force Analysis

为了简化计算，需要做如下假定：

（1）由于复合材料层合板较薄，忽略偏心载荷的影响；

（2）胶层的剪应力沿厚度方向均匀分布；

（3）复合材料为线弹性材料，胶层选用连接强度较高的韧性胶，并且只考虑弹性变形。

取搭接胶接接头的微元体进行应力分析，如图1（b）所示，微元体静力平衡方程为：

式中：G—胶层剪切模量；ui(i=1，2)—被胶接件纵向位移。

对式（11）求导可得：

对式（10）求导可得：

式中：A—根据边界条件确定的待定系数；

C—常数；

sinh(kx)—双曲正弦函数，且sinh(kx)=(ekx−e−kx)/2。

单搭接的边界条件［9］为：

将式（17）代入式（19）求得系数A为：

于是式（16）可表示为：

将式（19）带入式（10），求得胶层剪切应力τ分布函数为：

式中：cosh(kx)—双曲余弦函数，且cosh(kx)=(ekx+e−kx)/2。

设结构上下被胶接物刚度和强度相同，根据应力分布规律［9−10］，单搭接接头在受到拉伸载荷时，胶接端头处剪切应力最大，最先发生破坏。

将x=±l带入式（20），则胶层失效抗力Na：

式（21）中Na与l的曲线，如图2所示。

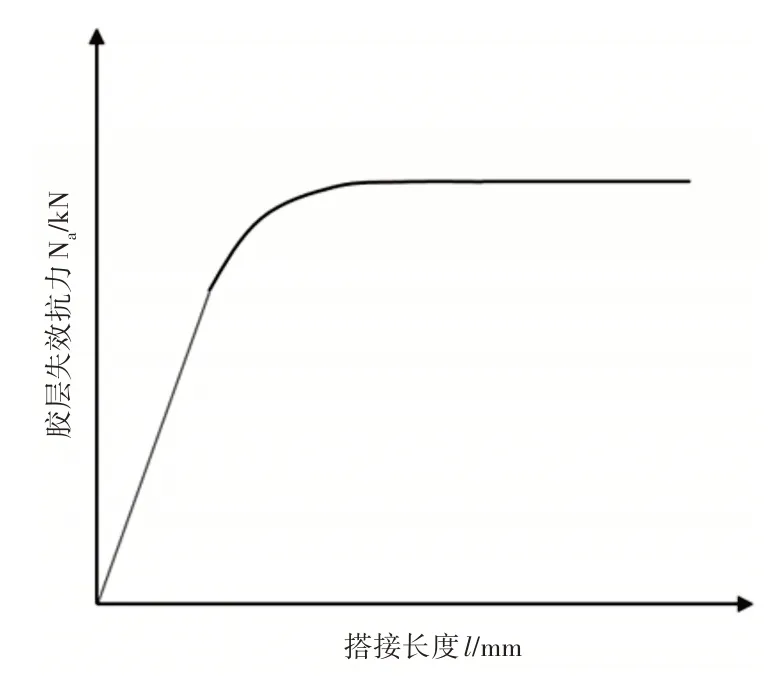
图2 胶层失效抗力与接头搭接长度的函数曲线Fig.2 Function Curve of Failure Resistance of Adhesive Layer and Lap Length of Joint

从图中可以发现胶层的失效抗力随搭接长度的增加而增加，当搭接长度到达一定值之后，胶层抗力趋于平缓。

4 胶接结构可靠性建模

对于复合材料层合板胶接单搭接结构的失效问题，结构中任意一个单元失效则判定胶接结构失效［11］。层合板采用首层失效原则，任意一个单层板失效则层合板失效。由n个层单元和1个胶层单元共n+1个失效元组成的串联系统，可靠性框图，如图3所示。其中di(i=1，2，…，n)为层合板各层单元，dn+1为胶层单元。

图3 串联系统可靠性框图Fig.3 Reliability Block Diagram of Eries System

可靠性分析中的随机变量包括合板纵向拉伸强度Xt、横向拉伸强度Yt、剪切强度S和胶层的剪切强度τP，以及层合板单元与胶层单元的共同随机载荷N。

首先对层合板强度分析，利用单层板的相关参数通过式（1）得到单层板的各方向的应力值；把应力值和单层板的各强度指标带入到Tsai−Hill失效判据式（2）得到由各单层板失效引起的层合板失效单元抗力Ni(i=1，2，...，n)。

接着对胶接结构的微元体进行弹性力学分析，带入胶粘剂的弹性常数得到胶层的剪应力分布函数如式（20）；根据应力分布规律，得到胶层单元抗力函数如式（21），把胶粘剂强度指标带入式（21）得到胶层失效单元抗力：Nn+1=Na。

对于单元独立的串联系统，通过抗力与载荷的差是否大于零判定各单元是否可靠，得到各单元的可靠度，各单元可靠度相乘得系统的可靠度。但是在本结构中各单元因失效载荷而相关，直接通过比较各单元的失效抗力，选取抗力最小值与载荷的差是否大于零判定系统是否可靠，从而得到系统的可靠度［12］。因此对各单元抗力Ni进行比较选取最小值Nmin=min(N1，…Nn，Nn+1)，与随机载荷N做差，得到复合材料件单搭接胶接结构的功能函数：

当各单云抗力最小值小于结构受到的轴向载荷时，功能函数G<0，则判定胶接结构失效；当各单元失效抗力最小值大于等于轴向载荷时，功能函数G≥0，则判定胶接结构可靠。

利用Monte−Carlo 数值模拟法[11]，对随机变量的概率密度函数抽取M个样本，统计失效样本点的个数Mf与总样本点个数M之比即为失效概率的估计值Pf。具体分析过程，如图4所示。系统可靠度R为：

图4 胶接可靠性分析流程图Fig.4 Flow Chart of Reliability Analysis of Composite Adhesive Structure

5 算例分析

已知复合材料层合板由三层玻璃/环氧单层板构成，铺层角度为［90，0，90］，单层板的厚度为t=0.3mm，单层板弹性常数为E1=35.37GPa，E2=8.78GPa，G=3.17GPa，v1=0.3；胶层的厚度ta=0.1mm，胶层弹性常数为Ea=3.5GPa，va=0.4；单搭接长度为L=17mm。各随机变量统计特征，如表1所示。计算单搭接胶接结构在随机轴向载荷N的作用下的可靠度。

表1 随机变量统计特征Tab.1 Statistical Characteristics of Random Variables

将相关参数分别带入到式（4）、式（21）中分别得到层合板的抗力和胶层的抗力。利用Monte−Carlo法对5个变量进行106次的随机抽样，得到各单元失效抗力最小值，与载荷N差值是否小于零判定胶接结构是否可靠，统计可靠次数与总试验次数的比值，得到结构的可靠度0.9762。

6 结论

（1）通过对层合板各单层板的应力分析，根据Tsai−Hill失效判据，得到各单层板失效引起的层合板失效的单元抗力。通过对单搭接胶接结构的弹性分析，得到胶层的剪应力分布函数；再根据应力分布规律得到胶层单元抗力。（2）建立了静态轴向拉伸载荷作用下单搭接胶接接头可靠性分析的概率模型，运用Monte−Carlo法对胶接结构各单元的强度指标进行随机抽样，得到各失效单元的最小值。通过抗力最小值与载荷的差是否大于零判定系统是否失效；可靠次数与总试验次数之比，即为胶接结构的可靠度。该方法为复合材料胶接结构的广泛应用奠定了理论基础。