改进T分布随机近邻嵌入改进聚类的机械故障分类方法
2023-03-19朱曦海伦易灿灿
朱曦海伦,易灿灿
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
1 引言
对于机械设备中无法直接诊断的故障常采用多种传感器对故障部位进行测量,然后对数据分析分析判断故障类型。该方法具有高效、不需拆解、诊断准确等优点。实际获得的信号通常是复杂的非平稳信号,无法直接诊断出机械的类型[1−2]。在实际工程运用中,采集到的数据往往需要大量的存储空间,降维后的数据除去无用的特征,利于计算[3]。对原始数据做出降维处理后,通过聚类分析可以看到数据在低纬空间的映射情况。聚类问题包含较多的簇,而聚类对象与簇之间并没有显式的对应关系,这是聚类问题的困难所在[4]。常用降维聚类的方法有PCA(主成分分析)、LDA(三层贝叶斯)、MDS(多位标度分析),PCA[5]方法虽然映射了数据的整体信息,但是没有映射出类间信息。LDA[6]方法虽然映射了分类信息,但是当样本信息大量存在时,类间信息不明,算法失效,还会出现过拟合数据。MDS[7](多位标度分析)保留了数据的原始相对关系,但是需要严格输入要求,较为耗时。
针对上述问题,将T−分布随机近邻嵌入与聚类问题相结合[8−9],高位数据空间结构映射到低维空间主要通过超图邻接矩阵和KL散度实现,之后再做聚类处理。
2 t−SNE聚类算法
2.1 T分布随机近邻嵌入
t−SNE算法是文献[10]在2008年提出的,属于流行学习算法,可对非线性的数据做处理。t−SNE算法在对数据进行降维的同时,可以保持数据在高纬空间中的低维流行结构,从而实现映射。
该算法的在高位空间和低维空间的相似性主要通过KL(Kullback−Leibler)散度衡量,在高位空间和低维空间分别采用高斯分布和t−分布,通过使这两个分布的相似性尽可能一致得到映射。
其余个体是0,矩阵H的每一列都用作特征。设高维数据点为X={x1,x2,…,xn},它对应矩阵H,在这里引入t−SNE,将其作为在低维空间的映射,高位空间的距离在低维空间保持相似,距离较大的结构保持较大的距离,距离较小的结构保持较小距离。Y={y1,y2,…,yn}为低维空间映射出的点,那么xi,xj在低维空间中所映射点的联合概率是:
式中:σi—方差,其中心在xi的高斯分布中。
yi,yj为低维空间的映射点,可由t−SNE计算,在理想条件时,可得到Qij=Pij,此时yi和yj需对xi和xj做出相似度较高的建模。通常Qij与Pij有误差,需要使得误差降到最小,使用代价函数来衡量误差:
式(5)梯度表示为:
这里使用梯度下降法对代价函数做最小化处理,将相对较大的动向量加入到渐变中,以加快优化过程并防止其陷入不适当的局部最小值。带动量项梯度变化用公式表示为:
式中:Y(t)—经过迭代t次后得到的解;
η—梯度变化中的学习效率;
α(t)—变化后的动量项。
2.2 改进聚类算法
在获得与H行相对应的低维空间数据点表示后进行聚类。如果在聚类过程中类的增长速率太慢,就会被认作是一个离群值,但是没有统一的标准来定义增长速率,这是使用者自行确定的,而且类选择代表会比较消耗时间。改进算法是对密度进行分层凝聚的聚类算法,作为簇终止条件,有必要预先确定簇数。
首先将每个数据对象视为一个单独的类,然后继续合并这些类,直到达到退出条件停止。改进算法对原始数据集中的点密度进行计算,然后计算偏差点集P,其余的点组成数据集S。根据数据集密度不同对进行分层,并对密度最高的两层和密度最低的两层进行分层聚类。基于两级聚类结果,对整个数据集S进行聚合和分层聚类。
最后,根据接近原理,将点集P中的点分为点集S中已经分类的点,从而完成了原始数据集D的聚类。改进的算法使用了密度分层技术,这不仅使算法更有效,而且还允许算法处理不同大小的类。步骤如下:
(1)在数据集D中找到每个数据点的密度,点密度是特定区域中的点数。该表达式定义为:
式中:dij—点i和点j的距离;
dc—截断距离。
(2)数据集D中有部分点为偏差点,选取其中部分密度最小的15%点排除,剩余的所有点为数据集S。偏差点是首先设置一个截断密度并找到小于截断密度的密度点集的过程,如下所示:
式中:ρc—预先设定的截断密度;
n—小于截断密度的点数。
(3)数据集S中最密集的20%点形成数据集B,根据聚合层次聚类方法将其分为大约2k个类别。获取数据集B的过程类似于查找偏差点的过程。i和j是不同的数据点,两个簇u和p之间的距离表示为:
(4)数据集S的最小密度点的大约25%组成了数据集L,根据聚合层次聚类方法将其分为大约2k个类别。基于层次聚类,根据凝聚的层次聚类方法,将整个数据集S聚类为大约k个类别。
(5)最后,P个数据偏差点被划分为最接近的S类,从而完成了所有D数据的分组。
改进的算法受参数截断距离和截断密度影响较小。整个收集过程都依赖于计算数据点之间的距离,而无需复杂的公式。改进了分层算法,在最高和最低密度层上进行分层分组的思想是提高算法的效率以及处理密度不均分布式数据集。
3 仿真数据分析
轴承主要用于机械设备的旋转零件,误差信号通常是非线性且不稳定的,并且包含大量的缺陷和噪声成分[11],从这些信号中提取故障特征是诊断故障的关键。
有许多仿真的故障模型,最经典的是Randall[12]提出的。模拟信号是:
式中:s(t)—周期性的冲击分量;A0—共振幅度;fr—调制频率;φA、φw、CA—常数;C—衰减系数;T—两次冲击之间的平均时间,T=—故障的特征频率;fn—谐振频率;n(t)—高斯白噪声的成分。
外圈故障、内圈故障和滚动元件故障为常见的轴承故障,模拟这三种故障将调制频率分别设置为fr=0,fr=fr,fr=fre。
需要指出的是,fr是转动频率,fre是保持器频率。外圈故障频率f0、内圈故障频率fi和滚动件故障频率f0,如表1所示。

表1 滚动轴承的故障特征频率Tab.1 Fault Characteristic Frequency of Rolling Bearing
部分参数,如表2 所示。采样频率和采样点分别设置为4096Hz和4096点。三种故障的时频域图,如图1所示。

表2 内圈故障仿真信号的参数选择Tab.2 Parameter Selection of Inner Race Fault Simulation Signal


图1 三种仿真信号的时频域Fig.1 Time−Frequency Domain of Three Kinds of Simulation Signals
对三组故障信号作频谱分析,可以看到轴承故障信号的频域特征变化不明显,仅通过频率特征对不同的故障进行识别较为困难,使用上述提出的方法15组信号进行计算。三种仿真信号的聚类分析图,如图2所示。

图2 提出方法仿真信号聚类结果Fig.2 Clustering Results of Simulation Signals Provided by the Proposed Method
从图2中可以看到,三种故障的信号不管是在2D图,还是3D图中均被分开,而且三种故障之间没有重叠部分,在3D图中的外圈故障有极少部分信号偏移,没有形成良好的聚类效果,总体来说三种仿真信号的核心点被正确地挑选出来。主成分分析和K均值计算结果图,如图3所示。

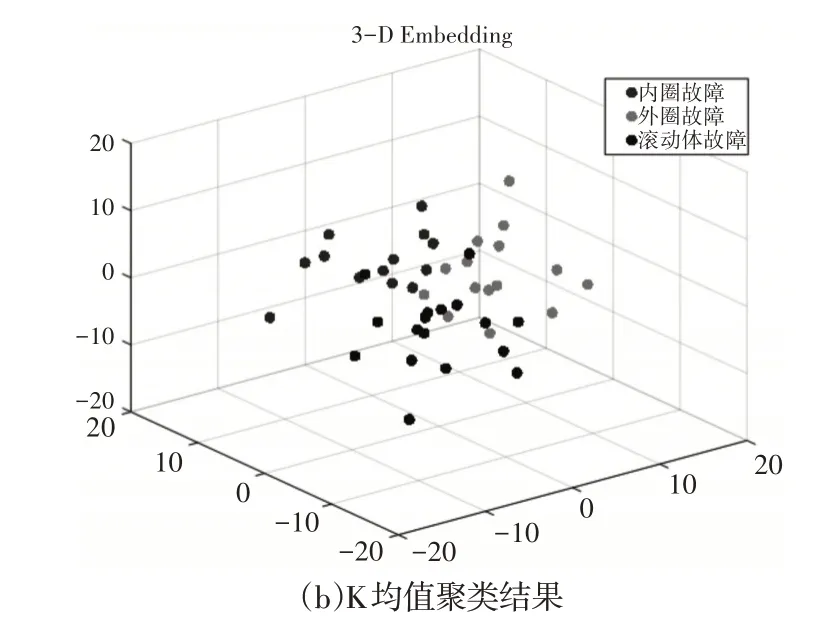
图3 PCA与K均值聚类结果Fig.3 Clustering Results of PCA and K−means
与图2 比较,聚类效果较差。可以看到,采用主成分分析(PCA)进行聚类的数据全部交错在一起,没有找到各个类别的聚类中心,类间也没有分开,没有达到理想的聚类效果。采用K均值聚类的数据有分开的趋势,部分数据找到类内中心,类间距离较主成分分析的效果要好,但是整体仍然没有达到理想的聚类效果。
4 实验数据分析
本实验分析采用的实验台装置原理图,如图4 所示。由电机、单级圆柱齿轮减速器和磁粉制动器组成,单级圆柱齿轮减速器由大小两个齿轮啮合在一起,齿数分别为37和20,模数为3。振动加速度传感器安装位置,如图4所示。
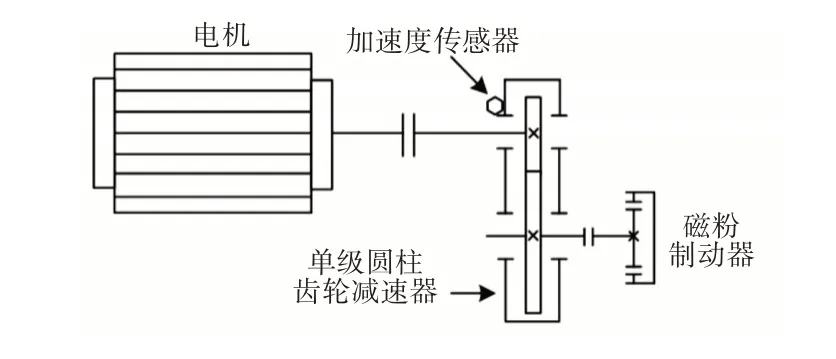
图4 齿轮故障实验装置及传感器布置示意图Fig.4 Schematic Diagram of Gear Failure Test Device and Sensor Arrangement
选取了正常、断齿、磨损工况三种齿轮,将三种齿轮分别安装在试验台中,采集振动信号。实验中不加负载,将高速轴转速调至363r/min,采样频率2000Hz,时间2s,本实验齿轮箱的尺寸比较小,而且具有较大的刚性,所以组装的折断齿,磨损和正常工作状态信号都受到齿轮固定螺栓振动的影响。15个信号组的时频域图,如图5所示。对信号组的频谱分析表明,信号的频域特征没有明显变化。
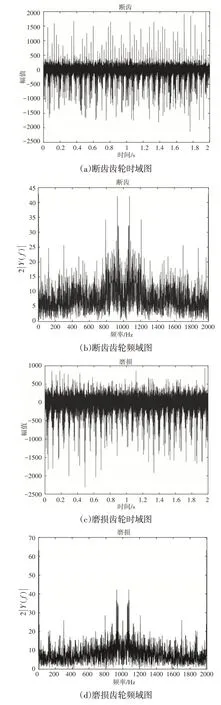

图5 三种齿轮的时频域图Fig.5 Time−Frequency Domain of Three Signals
下面采用齿轮故障数据集对聚类算法的分类效果进行测试,同时引入常用聚类算法作为对比。聚类效果的2D图,如图6(a)所示。从图中可以看到各类别相互重叠,没有完全分开;齿轮故障数据集的分布,如图6(b)所示。从图中可以看到,数据集包含三类数据,三类数据的核心点被正确地挑选出来;采用的十五组数据均被准确地聚类,类内之间没有重合情况,类间有重合情况,因为少量数据存在较大的相似度。

图6 提出方法齿轮故障聚类结果Fig.6 Gear Fault Clustering Results by the Proposed Method
为了说明该方法的效果,采用主成分分析的聚类方法和K均值聚类算法作为对比,运用主成分分析的聚类结果,如图7所示。从图中可以看到三类数据重合在一起,类间与类内均没有分开,而且同类数据出现了丢失的情况,没有达到聚类的效果。采用K 均值算法的聚类结果,如图8 所示。可以看到与主成分分析的结果相比,有明显的改善效果,两类数据已经到达了聚类效果,少量数据存在重合,第三类数据出现了大量丢失情况,没有达到聚类效果。
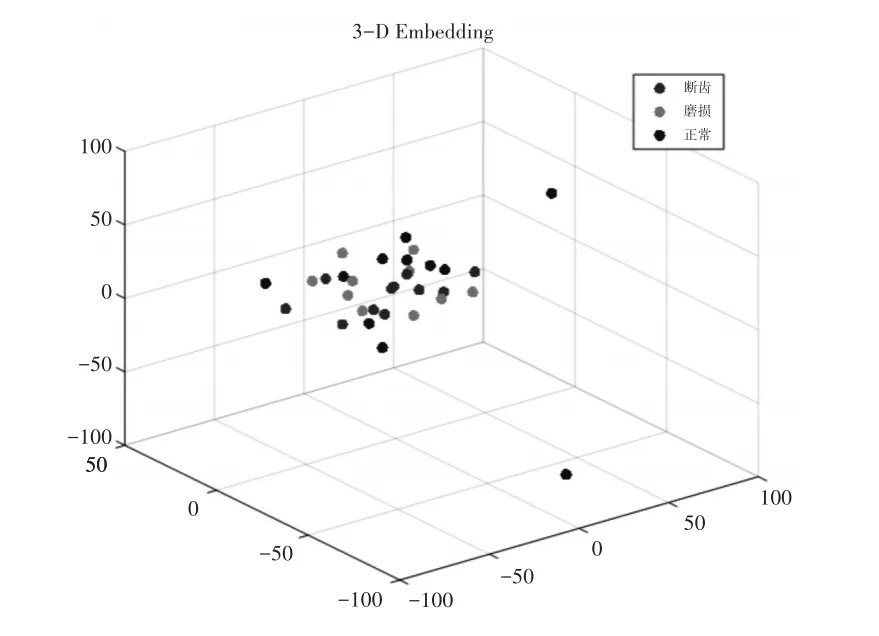
图7 主成分分析聚类结果Fig.7 Clustering Results of Principal Component Analysis

图8 K均值聚类结果Fig.8 Results of K−Means Clustering
与基于相空间和T分布随机近邻嵌入的聚类方法相比,整体数据集的聚类效果并不明显,没有达到完整的聚类效果。为了量化对比3种聚类算法的分类效果,分别计算了3类数据的分类正确率,如表3所示。

表3 不同方法数据分类正确率Tab.3 Data Classification Accuracy by Different Methods
5 结论
通过T分布随机近邻嵌入聚类方法将高维空间结构高度相似映射到低维空间,并且使用改进的聚类算法得到最后的结果。通过轴承仿真数据和实验测得的齿轮故障数据分析表明:
t−SNE算法与改进的密度聚类算法相结合可以对数据进行聚类分析,而且改进的t−SNE 聚类算法比PCA、K 均值聚类算法明显地提高聚类质量,获得了更加优越的效果。因此,基于t−SNE降维特征提取方法改进的聚类算法能够适用于机械设备故障诊断中。
