运载火箭风场高精度拟合方法

胡瑞光，钟文安，宋征宇，路坤锋，潘 豪，邵梦晗，王昭磊

(1. 北京航天自动控制研究所，北京 100854； 2. 西昌卫星发射中心，西昌 615600； 3. 中国运载火箭技术研究院，北京 100076)

0 引 言

随着运载火箭轻质化发展，新一代运载火箭对箭体结构的气动承载能力提出更高的要求，需要将气动载荷在飞行过程中控制在一定的范围。

在运载效率提升方面，当前迫切需要解决的是减小结构质量、降低结构强度的需求与火箭大气层内飞行时可承受气动过载有限、安全稳定飞行的矛盾。提升运载能力要求降低结构质量和强度，这会带来火箭承受气动载荷与控制力矩相互作用而形成的弯矩能力的严重下降，给火箭大气层内的安全稳定飞行带来挑战。为满足运载效率提升的同时，避免火箭承受过载超过结构强度要求，需要实施高效的风场干扰减载控制。

因此，研究能够在线进行气动风场拟合与预示、智能实时减载等关键技术，对运载火箭的安全性、可靠性具有十分重要的意义。

文献[1]明确指出，目前国外很多运载火箭的制导系统将实时测量的风场数据应用在其制导算法里面，而不再使用基于月度平均风场的离线风修弹道设计，从而大幅度降低由于风场精度不够带来的各种不确定性风险。

为了实现在线实时减载，一般需要具备射前一小段时间的探空气球实测数据，然后将实测数据以插值风表的形式装载进制导计算机中；或者对实测数据进行低阶多项式曲线拟合，并将拟合系数装载进制导计算机中；实际飞行时，根据飞行高度进行查表或多项式计算即可得到实际风场[2]。

1990年，“德尔塔”运载火箭对发射时刻2小时前的风场进行曲线拟合，实现了基于在线实时风场的减载制导[3]。具体地，“德尔塔”运载火箭采用最小二乘三阶多项式对北向和东向风速进行了拟合，并将拟合参数在发射前10分钟装载进制导计算机[4]。

我国风场干扰减载技术的相关研究工作早在1995年就已经成功应用于运载亚洲二号卫星和回声一号卫星的CZ-2E运载火箭上[5]。目前，我国的运载火箭大都使用弹道风修正和攻角或加速度计主动控制的方法进行减载控制[6]。弹道风修正是通过射前实测高空风数据，对火箭飞行程序角进行离线修正，使火箭在预报风场作用下飞行合成气动攻角最小，从而降低火箭飞行气动载荷。该方法原理简单，较易实现，在风场比较稳定的情况，减载效果较好，目前已广泛应用于中国现役火箭[7]。但该方法实时性不强，对风切变适应能力较差，过于依赖射前预报风精度，因此射前弹道风修正后通常会留有一定的设计余量，用于包络高空风切变和预报风场的不确定性，对风载荷的实时不确定性抑制能力较差，导致火箭不能做到全天候发射。

综上所述，建立实时风场的精确模型对于未来运载火箭的风场干扰减载控制很有帮助。同时，风场数据的采集时刻距离发射时刻越近越好，这就要求风场建模不但精度要高，而且建模速度要快，才能满足实际工程需要。

风场建模问题属于典型的曲线拟合问题，最常用的方法有插值法、最小二乘法、人工神经网络法等。文献[8]采用4层BP网络反演海面风向，并根据经验公式确定隐含层节点数取值范围，在大量训练数据的基础上，取得了较好效果。文献[9]采用最小二乘法对舱壁温度数据进行拟合，其温度曲线较为光滑，最小二乘法使用阶数也比较低。文献[10]提出的基于三层BP网络的滚转角粗对准模型可在任意失准角范围内快速完成粗对准，其适用角度广泛性和快速性明显优于传统方法；其中的隐层节点数也是根据经验选取。文献[11]采用最小二乘法对高超声速飞行器的升力系数、阻力系数和升阻比进行拟合，其数据点数为7。文献[12]采用分段最小二乘多项式、三层BP网络等方法对MEMS陀螺X轴、Y轴、Z轴数据进行拟合，试验结果表明三层BP网络的拟合效果明显优于最小二乘分段拟合方法，其中的隐层节点数也是根据经验选取；并明确指出，最小二乘分段拟合在分段间隔较小时，计算参数多，计算量大；分段间隔较大时，拟合精度较低，分段间隔处存在较大振荡。

通过对上述文献的综合分析比较，可以看出，最小二乘多项式拟合适合于曲线光滑、数据点偏少的场景，对于较大数据量、曲线复杂的场景，BP网络的拟合效果明显优于最小二乘多项式拟合及其分段处理形式。另外，BP网络的隐层节点个数往往根据经验公式或实践经验确定。

运载火箭风场实际曲线较为复杂。因此，针对运载火箭风场拟合问题，本文设计了一种基于最少参数神经网络的高精度风场拟合方法，只使用一套框架即可完成风速和风向的拟合，并提出拟合网络隐层节点数的下确界公式。大量的试验结果表明，最少参数神经网络的拟合精度要远高于最小二乘多项式拟合方法及其分段形式，同时验证了下确界的相对合理性。

1 运载火箭风场拟合模型

1.1 问题提出

考虑运载火箭飞行高度x，在高度x处的风场为(ν,α)，其中ν为风场速度，α为风场朝向。可以认为风场速度和风场朝向皆是飞行高度的函数

(1)

式中：θν和θα分别为对应函数的参数。

图1 运载火箭风场高精度拟合流程Fig.1 Flow chart of the high-precision fitting for the wind field of launch vehicles

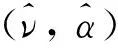
(2)

式中：D( )为一种误差度量函数。

在式(1)中，风场速度和朝向分别使用一套独立的参数，也可以使用一套参数完成整个风场的拟合。具体地，

(ν,α)=fn(x,θn)

(3)

则拟合问题可表示如下

(4)

1.2 飞行高度区间选择

在实际飞行过程中，大风区风场往往对运载火箭的飞行安全具有较大影响，大风区以下空域和以上空域的风场影响较小,因此，只需要对运载火箭大风区的风场进行拟合即可[2]。

大风区飞行高度一般为4～20 km，本文只对该飞行高度区间的风场进行拟合。

1.3 最小二乘多项式拟合

对离散的数据进行拟合的目的是为实验数据寻求到一条最佳拟合曲线，通过对曲线的相关特征或参数的分析研究，试图找到蕴含在数据内的规律[13]。从计算方法的角度看，曲线的拟合与函数插值法比较类似，拟合是寻求一条曲线，使其能与观测数据“最靠近”。

最小二乘多项式拟合是曲线拟合的一种经典方法，广泛应用于多个实际工程领域[14]。最小二乘准则就是使所有离散点到曲线的距离平方和最小。最小二乘多项式拟合反应了数据点的总的趋势，消除了其局部波动，适用于杂乱无章的无序离散点拟合，最小二乘多项式拟合对于有序的离散点拟合效果不够理想，其不可能使得每个点都反映线形趋势关键变化[15]。

设已知n个数据点(xi,yi),i=1,2,…,n，则最小二乘多项式拟合的曲线为

f(x)=a0+a1x+a2x2+…+amxm

(5)

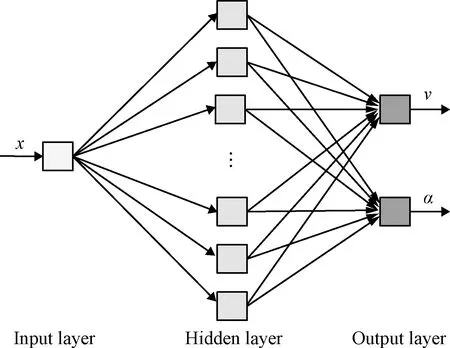
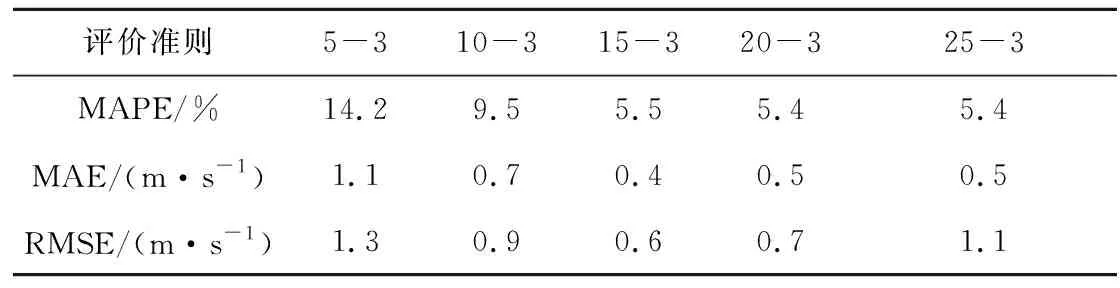
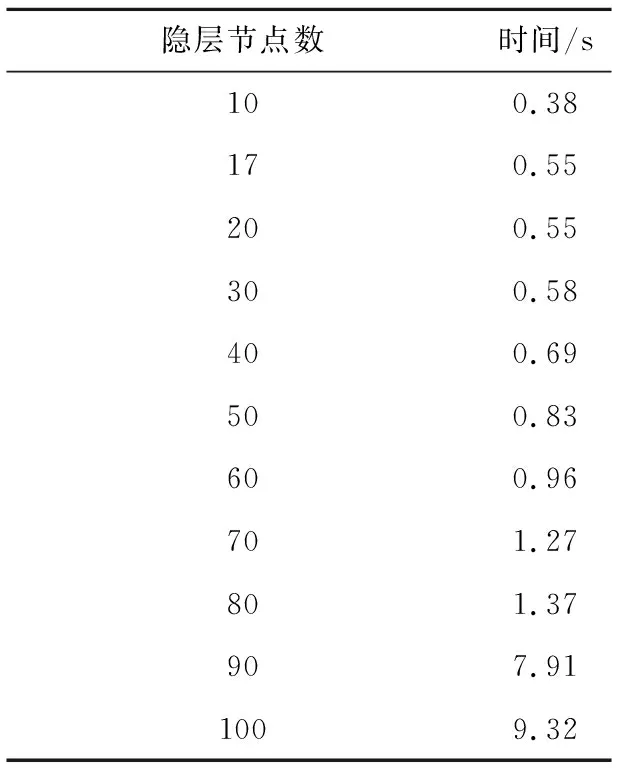
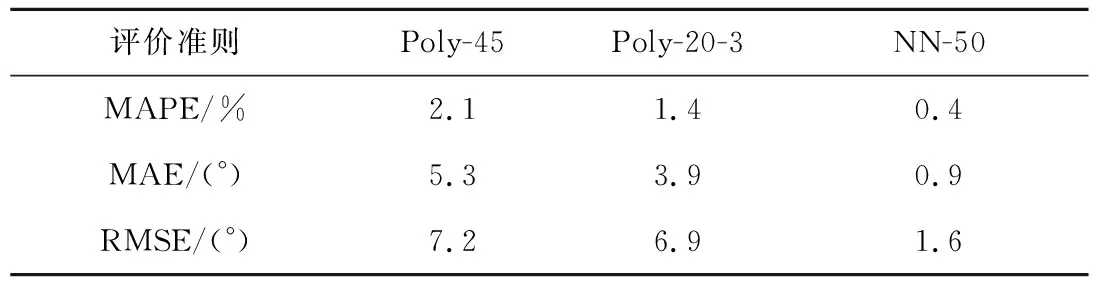
式中：m为多项式阶数。一般地，m

在用最小二乘法估计参数时,要求观测值yi的偏差的平方和为最小。即

(6)

式(6)的值为最小。

根据最小二乘法原理，式(6)对系数的偏导数为0，可得

(7)

上式可表示成XA=Y，则A=X-1Y，可得到最小二乘多项式拟合曲线的系数值。可以看出，该方法具有坚实的理论基础。在实际应用中，根据求得的系数值，采用式(5)即可得到需要的拟合值。

1.4 最少参数神经网络拟合

以卷积神经网络为代表的深度学习方法是近几年人工智能领域的主流框架，在图像处理、语音处理、机器博弈的领域得到了广泛应用[16-19]，并取得了突破性进展。

对于运载火箭风场高精度拟合问题，虽然卷积神经网络可能会取得很好的效果，但是卷积神经网络包含层级过多，相应的网络结构参数也过多。因此，本文采用传统的BP神经网络对运载火箭风场进行拟合。

单隐层BP网络的应用最为普遍，它包括输入层、一个隐含层和输出层。上下层之间实现全连接，而每层神经元之间无连接。BP网络的学习可分为两个过程:工作信号的正向传播和误差信号的反向传播。

根据万能逼近定理(Universal approximation theory, UAT)，如果隐层节点是可以根据需要自由设置的，那么用三层S状的I/O特性的节点可以以任意精度逼近任何具有有限间断点的函数。如果BP网络的各节点选用非线性转移函数，则对于任何相关问题从理论上都可以用三层前馈网络来加以解决[20]。因此，本文使用三层BP网络进行运载火箭风场高精度拟合。

三层BP网络的函数形式为

y=f2(W2×f1(W1×x+b1)+b2)

(8)

式中：x为输入向量；y为输出向量；W1为第一层权重矩阵；b1为隐含层偏置向量；f1( )为隐含层传递函数；W2为第二层权重矩阵；b2为输出层偏置向量；f2( )为输出层传递函数。

三层BP网络曲线拟合的过程是采用训练的方式得到权重矩阵和偏置向量。网络训练一般采用梯度下降法和后向传播的方式，使得损失函数最小，这里不再赘述。

对于用三层BP网络拟合运载火箭风场，本文采用一个网络同时完成风速和风向的拟合。对于这类网络，其输入层只有一个节点，代表飞行高度，输出层有两个节点，分别代表风速和方向。风场拟合网络结构如图2所示。

图2 最少参数风场拟合网络Fig.2 The least-parameter wind fitting neural network

风场拟合网络的传递函数设置如下

(9)

f2(x)=x

(10)

隐含层传递函数保证了网络框架的非线性，输出层传递函数保证了曲线拟合的准确性。

设隐层节点数为nh，将式(9)和(10)代入式(8)，可得

(11)

根据函数逼近论，上述问题就是在一组基函数所张成的空间中寻找函数的近似表达使其误差最小，每一个隐含层节点对应一个基函数，这些基函数是通过改变传递函数f1的权重和偏置得到的。神经网络的学习过程本质上是在学习基函数。

假设两个隐层节点的基函数及其线性组合为

(12)

其曲线如图3(a)所示，可以看出线性组合呈现柱状。若权重和偏置取不同的值，可以得到不同的基函数及其线性组合

(13)

其曲线如下图3(b)所示，可以看出呈现尖峰状。

图3 网络基函数线性组合Fig.3 The linear combination of basis functions

由图3可以看出，两个不同的基函数的线性组合一般呈柱状；当基函数本身的权重比较接近时，或者基函数本身的偏置比较小时，线性组合会呈尖峰状。用于组合的权重和偏置可以改变组合结果的尺度。

万能逼近定理解决了函数逼近论中的稠密性问题，而隐层节点数的选择是函数逼近论中的复杂性问题，即研究网络隐层的拓扑结构与逼近速度的问题。隐层节点的数目直接关系着BP网络的学习效率和泛化能力，也直接决定了网络的参数数量。如果隐层节点太少，即如图3(a)所示，网络只包含有限的柱状组合，则无法完成对复杂曲线的拟合。如果隐层节点太多，则网络包含太多参数,当对这些参数进行随机初始化并训练时，有限的数据样本远远不足以调制这些参数，训练完成后网络仍然包含一些类似的权重和偏置，结果必然如图3(b)所示，呈现出尖峰效应，而且隐层节点越多，尖峰效应越明显，拟合的精度也越差。

文献[21]设计了神经网络逼近速度的一类上界

(14)

曹飞龙等[22]设计了神经网络逼近速度的一类下界

(15)

理论上，根据逼近上界可以确定满足误差要求的隐层节点最小值，比最小值还要小的节点数值会导致误差变大；根据逼近下界可以确定满足误差要求的隐层节点最大值，比最大值还要大的节点数值也会导致误差变大。根据夹逼定理，在最小值和最大值之间必然存在一个最优值，使得误差最小。

实际应用中，要精确确定隐层节点数目又是困难的，目前对BP网络的隐层节点数目的确定并没有一个公认或统一的理论作指导。常用的选择方法有试凑法、经验公式法、递增法、递减法等。在实际的设计过程中，只有根据以往的经验，并对大量的试验结果进行分析、比较，综合应用多种方法才能找到一个较好的节点数。

常用的经验公式有[23]

nh=(ni+1)×no

(16)

(17)

(18)

式中：nh为隐层节点数；ni为输入层节点数；no为输出层节点数；a为1～10之间的常数。

显然，上述经验公式只考虑了网络本身因素，没有考虑要拟合的数据信息对隐含层节点数的影响。根据前面关于柱状组合的描述，网络隐层节点数不但与输入输出的维度有关系，而且与复杂曲线的样本点数量也有关系。

根据信息论，多项式曲线拟合与神经网络曲线拟合都可看作是采用相应的基函数对风场曲线进行数据压缩。本文借鉴无损压缩中的熵编码原理，提出拟合网络隐层节点数的下确界公式

nh≥ni×lbnd×no

(19)

式中：nd为拟合数据样本个数。

熵编码是一种独立于信息源具体特征的无损压缩方法。因此，式(19)可以广泛应用于多种场景，例如火箭发动机振动信号分析与降噪、火箭箭体弹性模态分析、弹道规划与预测等。也可以广泛应用于有类似数据处理任务的领域，例如音视频处理、智能驾驶等。

网络结构也不限于单输入双输出的场景，也可应用于多特征联合分析的应用场景，多特征可用多个输入节点表示,输出节点自然不受限制。例如对图像分类任务来说，把二维图像展开成一维向量，对应着多个输入节点。一般地，图像分类数据库包含的图像样本非常多，根据式(19)，如果用单隐层网络完成任务，其隐层节点数会变得非常大。这也是卷积神经网络包含着多个隐含层和非常多参数的原因之一。

1.5 拟合精度评价准则

本文采用三个准则评价运载火箭风场拟合误差，分别是平均绝对值比例误差(Mean absolute percentage error，MAPE)，平均绝对值误差(Mean absolute error，MAE)，均方根误差(Root mean squa-red error，RMSE)，其定义如下

(20)

(21)

(22)

三个准则从不同的侧面对拟合效果进行定量评价，构成了曲线拟合的完备评价体系。

2 仿真校验

首先对最小二乘多项式拟合及其分段形式进行充分验证，然后对最少参数神经网络拟合进行充分验证，接着将两种方法进行了对比。

2.1 最小二乘多项式拟合结果

针对飞行高度区间4～20 km，每50 m采样一次，因此，本文拟合数据样本个数为321。最小二乘多项式拟合的关键参数是多项式的阶数；另外，需要对风速和风向分别进行拟合，即需要用两套参数来完整描述运载火箭高空风场。本文将多项式阶数取值设计为从10到50，并每隔5阶计算一次拟合结果。部分拟合曲线如图4所示，其中Poly-10表示10阶多项式，以此类推。在PC机上，不同阶数多项式的拟合时间皆小于0.01 s。

图4 最小二乘多项式拟合结果Fig.4 The least-square polynomial fitting results

采用三个评价准则，可得最小二乘多项式拟合的误差如表1和表2所示。可以明显看出，在阶数较小的情况下，最小二乘多项式的拟合结果偏差较大。对于阶数较大的情况，虽然理论上应该获得较好的拟合结果，但是实际的拟合结果也具有较大的偏差，这种现象对于较高的飞行高度更加明显。只有阶数适当的情况下，最小二乘多项式方法才具有较好的拟合性能。

表1 最小二乘多项式风速拟合误差Table 1 The least-square polynomial speed fitting errors

表2 最小二乘多项式风向拟合误差Table 2 The least-square polynomial angle fitting errors

同时，本文也采用分段多项式拟合的方式对火箭风场进行拟合。具体地，将高度区间4～20 km分为三段，即4～9 km、9～14 km、14～20 km；并在每一段采用最小二乘多项式进行拟合，阶数分别为5、10、15、20、25。部分拟合曲线如图5所示，其中Poly-5-3表示3段5阶多项式，以此类推。

图5 分段多项式拟合结果Fig.5 The multi-segment polynomial fitting results

采用三个评价准则，可得分段多项式拟合的误差如表3和表4所示。可以明显看出，分段多项式的拟合结果要比不分段的情况有所改善。但是，在阶数较小的情况下，分段多项式的拟合结果误差也较大；另外，对于阶数较大的情况，在分段间隔处有明显的振荡现象，而且阶数越大，振荡越强，拟合误差也越大。

表3 分段多项式风速拟合误差Table 3 The multi-segment polynomial speed fitting errors

表4 分段多项式风向拟合误差Table 4 The multi-segment polynomial angle fitting errors

2.2 最少参数神经网络拟合结果

本文拟合数据样本个数为321，根据式(19)可求得隐层节点数下确界为17。

本文将隐含层节点数取值设计为从10到100，每隔10计算一次拟合结果，并在下确界17处也进行了拟合，部分拟合曲线如图6所示。其中NN-10表示用10个隐含层节点进行拟合的结果，以此类推。

图6 最少参数神经网络拟合结果Fig.6 The least-parameter neural network fitting results

为了公平比较，对不同隐层节点数的网络皆进行充分训练，当隐层节点数较少时，训练次数为200，拟合网络很快收敛；当隐层节点数较多时，NN-90和NN-100的训练次数为2000，也达到稳定状态。拟合时间如表5所示。

表5 不同隐层节点数网络拟合时间Table 5 The network fitting time with different number of hidden layer’s notes

采用三个评价准则，可得最少参数神经网络拟合的误差如表6和表7所示。可以明显看出，在隐含层节点数小于本文提出的下确界的情况下，最少参数神经网络的拟合结果偏差较大。对于隐含层节点较多的情况，拟合结果的三个评价准则值较好，然而NN-60的拟合曲线已经有一定的尖峰效应，即拟合值有明显的偏离点；而且隐层节点数越多，尖峰效应越明显，拟合误差越大，如图6中NN-100所示，这对于实际工程应用有较大的弊端。只有隐含层节点个数适当的情况下，最少参数神经网络才具有较好的拟合性能。

表6 最少参数神经网络风速拟合误差Table 6 The least-parameter neural network speed fitting errors

表7 最少参数神经网络风向拟合误差Table 7 The least-parameter neural network angle fitting errors

综合上述分析，当隐含层节点数小于下确界时，网络拟合误差较大；当隐含层节点数大于或等于下确界时，拟合误差迅速变小；当隐含层节点数过多时，拟合误差会变大。充分说明了本文提出的隐含层节点数下确界的相对合理性。

2.3 拟合结果对比

前述两小节对最小二乘多项式拟合及其分段形式与最少参数神经网络拟合分别进行了分析与评价；只要阶数和隐含层节点数适当，两个都能得到较好的拟合结果。因此，为了实现运载火箭风场的高精度拟合，需要对两者进行对比分析。

图7和图8对45阶最小二乘多项式、3段20阶多项式和50个隐含节点的BP神经网络的拟合误差曲线进行了展示，三者皆是对应方法中的最好拟合结果。可以明显看出，在大多数高度值上，BP网络的拟合误差都是最小的；多项式拟合的误差是最大的，分段多项式的拟合误差处于中间位置；同时，分段多项式拟合有一个显著的特征，即在分段处有非常明显的振荡效应。表8和表9的评价指标值也充分说明了这一点。

图7 风速拟合误差曲线Fig.7 The curve of wind speed fitting errors

图8 风向拟合误差曲线Fig.8 The curve of wind angle fitting errors

表8 风速拟合误差比较Table 8 The comparison of wind speed fitting errors

表9 风向拟合误差比较Table 9 The comparison of wind angle fitting errors

另外，最小二乘多项式拟合需要两套参数才能完成风场拟合，分段多项式拟合更是需要多套参数才能完成风场拟合；最少参数神经网络拟合只需要一套参数即可完成风场拟合。

由拟合误差曲线和误差指标值可以明显看出，最少参数神经网络的拟合结果要明显好于最小二乘多项式及其分段形式的拟合结果。具有50个隐含节点的三层BP神经网络具有很好的拟合精度，同时参数数量接近最少，使用便捷，具有较高的工程应用价值。

3 结 论

对于运载火箭高空风场，本文利用最小二乘多项式及其分段形式和最少参数神经网络进行了拟合，分别对比了不同阶数多项式及其分段形式的拟合结果和不同隐含层节点个数神经网络的拟合结果，并对比分析了三类方法的最好结果。仿真试验表明，最少参数神经网络的拟合效果明显好于最小二乘多项式及其分段形式的拟合效果，而且只需要一套参数即可完成任务。同时，对神经网络在不同隐含层节点个数情况下的结果进行了细致的分析，体现了本文提出的隐含层节点数下确界的相对合理性，明确了具有最好拟合效果的隐含层节点个数，为后续的实际工程应用打下了坚实的基础。