航天员出舱牵引构型设计与结构响应性能评估

杨全欧，李志辉，秦远田，包为民

(1. 中国空气动力研究与发展中心，绵阳 621000； 2. 南京航空航天大学航天学院，南京 211106；3. 中国航天科技集团有限公司，北京 100048)

0 引 言

中国空间站正处于建造阶段，随着航天员的入驻，空间站核心舱的出舱作业不断开展。舱外活动技术已成为支撑空间站运行和拓展应用服务不可或缺的关键技术，在轨可靠性和在轨资源的使用效率成为重点发展的方向[1-2]。为提高舱外工作效率，在传统可靠工作基础上，需要重点突出对航天员安全性及任务成功的风险分析研究[3]。安全绳是目前航天员出舱必备的安全设备，而脐带是保持氧气、水分及电力等的输送。绳索和工具对舱外活动造成的操作影响是不可避免的[4]，脐带与安全绳过多会造成结构冗余。如今国际上的舱外航天服自带生命支持系统，少有长脐带，但仍然采用安全绳。Minor等[5]研究了可远程释放的机器人抓手和控制系绳长度的卷收器组成的系绳管理系统，可从远距离远程释放和收回他们的安全系绳，并未解决频繁锁挂的问题，机器人抓手的体积和质量较普通挂钩大，增加了宇航员的载荷负担。陈学文等[6]使用基于位置的仿真方法计算了安全绳的变形，建立了航天员舱外活动安全绳操作仿真系统，其中考虑到绳索在无重力作用下的柔性变形，切合绳索飘动的真实情形，同时碰撞处理的不足也反应了绳索问题的难点所在。张大羽等[7]采用非线性欧拉梁单元分析了空间天线绳索的运动问题，可作为安全绳在张紧状态下的设计参考。中国空间站航天员在2021年执行了出舱任务，除了机械臂的协助部分，想要达到舱外较远位置，必须连续对两条安全绳的挂钩进行轮流锁挂，该过程会大量占用航天员舱外活动时间，而两条安全绳来回切换，存在一定的缠绕概率。本文拟设计的航天员出舱牵引方案，通过导轨机构能使航天员快速到达舱体外表面的绝大部分，避免了来回切换安全绳挂钩的重复动作，以期解决安全绳便利性问题，明显缩短舱外活动所需要的辅助时间。

针对空间飞行器结构特点，一般要求其形状稳定，热环境引起的结构刚度变化会造成承载能力下降，不管空间环境温度变化有多大，结构形状的变化要尽可能地小[8-9]。本文设计的牵引系统直接暴露在太空环境中，牵引导轨作为牵引系统中的主要结构件，需要进行热力耦合分析。Soares[10]采用一种稳定的局部定义显式方法来发展热-力学耦合模型计算分析，自适应地采用改进的中心差分法和前向差分法，不考虑其时间解的稳定性限制，并对平板和悬臂梁模型进行了分析，但并未对三维模型进行分析。Li团队[11-14]基于热弹性动力学与热传导方程，提出了一种基于外部环境影响的结构热力响应有限元计算模型及算法软件，来模拟材料的动态热弹性耦合问题，在时域上离散动态热弹性与热传导模型，设计并讨论了求解热力耦合方程的有限元计算格式。在此基础上，本文发展可用于牵引导轨的热力耦合响应计算模型与有限元算法，验证极限热载荷下安全工作的可靠性。牵引盘与导轨的接触力是最大的载荷所在，通过静力学分析进行导轨强度校核。

1 航天员出舱牵引系统构型设计

在航天员出舱工作中，传统安全绳作用时需要两个挂钩进行频繁交替挂接，会产生较长的辅助时间，为此本团队进行了航天员出舱牵引系统的构型设计，可以提升太空行走的流畅度，减少航天员在安全绳挂接上的繁琐过程。本系统针对航天员太空行走便捷性而设计，是航天员舱外作业的辅助装置，含有舱外导轨、牵引盘、搭接桥及牵引绳等四个部分，总体如图1所示。牵引绳代替原有的安全绳，连接于航天员与牵引盘之间，牵引盘运动在舱外导轨中，可沿导轨方向自由滑动，舱外导轨固定在舱体表面，航天器对接舱段之间的导轨采用搭接桥形式进行连接，航天员通过攀爬扶手在舱体表面进行运动，由此航天员可以在多个舱段表面进行作业。

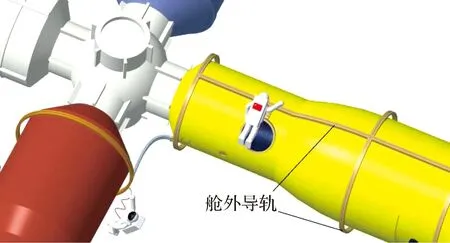
图1 航天员使用出舱牵引系统示意图Fig.1 Extravehicular traction system used by astronauts

1.1 舱外导轨

舱外导轨是航天员进行太空行走的导向结构，作为防止航天员脱离舱体表面的主要承力装置。导轨在舱体外表面部署情况如图1所示，在舱体的径向与轴向均进行部署，可以使航天员接触到舱体大部分外表面。导轨的截面如图2所示，牵引盘可在导轨中来回滑动，要严格限制其运动方向而不发生脱轨，则必须保证导轨的强度要求。

1.2 牵引盘

牵引盘运动于导轨当中，如图2所示，其机构可提供两个自由度，沿导轨滑动和绕自身轴向转动。

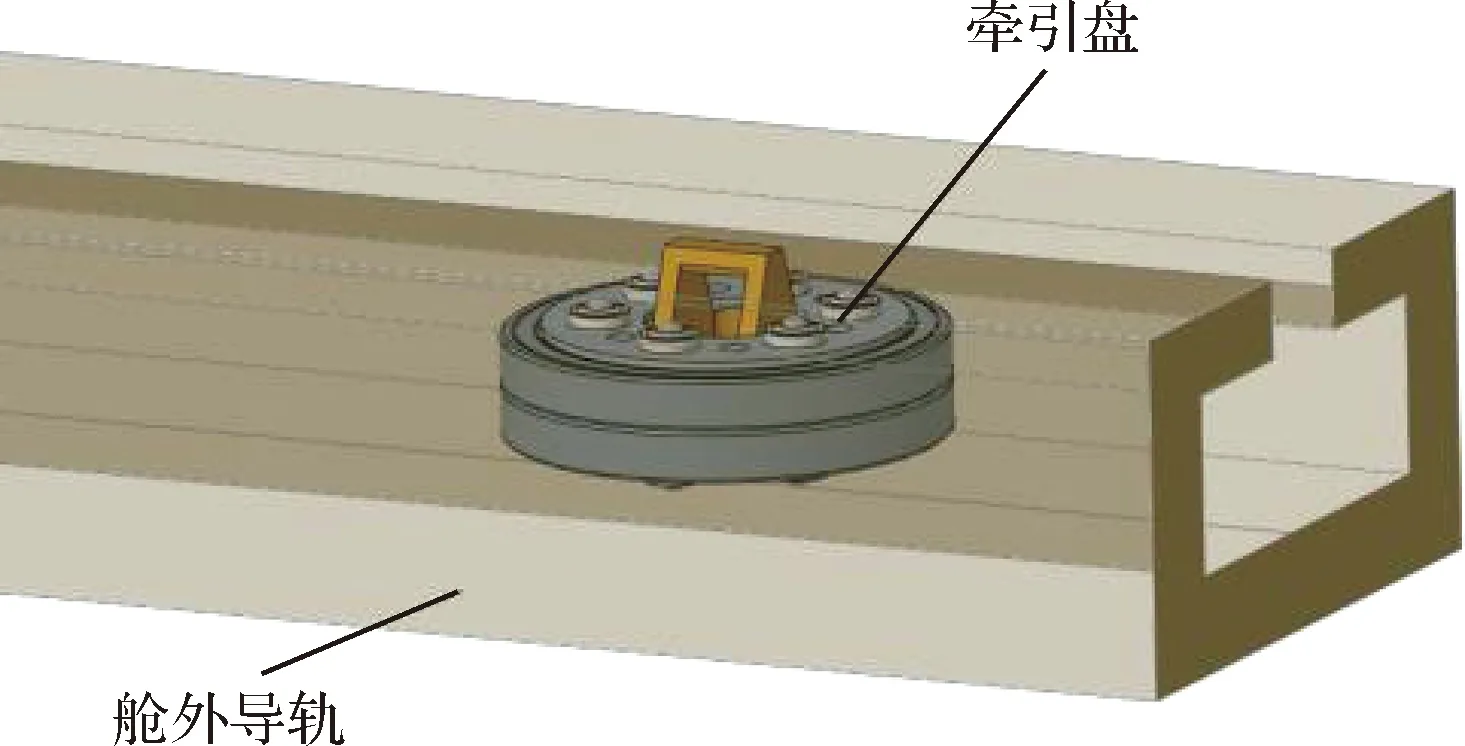
图2 牵引盘在导轨中安装图示Fig.2 The traction disk is installed in the guiding rail

牵引盘的整体结构如图3所示，最外围的轴承提供绕自身转动的自由度。上下面各有6个万向滚珠，使得其在接触导轨过程中可以自由滑动，且在牵引盘的轴向具有微小的弹性行程，以此减缓碰撞过程中产生的冲击力。

图3 牵引盘整体图示Fig.3 Schematic diagram of the traction disk

1.3 搭接桥

搭接桥可以从一个舱体转动到另一舱体，形成不同舱体之间的导轨贯通，实现航天员从一个舱体过渡到另外一个舱体。如图4所示，搭接桥一端为铰链机构，另一端为楔块机构，其中间部位与导轨结构一致，在曲率比较大的位置，根据牵引盘可通过情况对导轨槽的上下间隙进行设计。

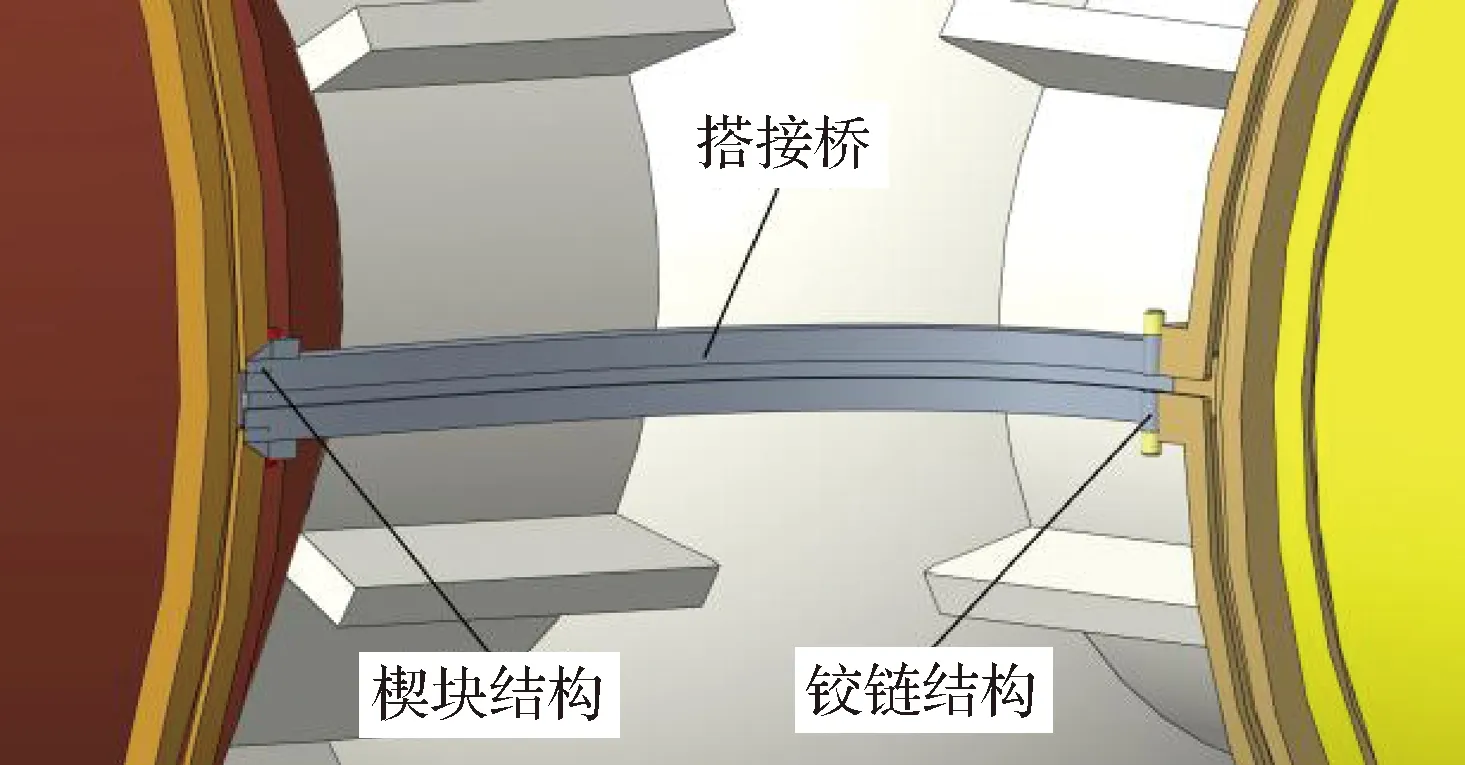
图4 搭接桥结构示意Fig.4 Schematic diagram of overlapping bridge structure

1.4 牵引绳

此处设计的牵引绳与安全绳效果相同，但在航天员采用牵引绳的移动过程中，不需要在两条安全绳之间进行来回切换，避免了繁琐的挂钩操作，也降低了各种绳索间缠绕的概率，如图5所示。

图5 航天员通过牵引绳与舱体连接Fig.5 The astronaut is connected to the capsule by a tow rope

2 结构响应热力耦合有限元算法

2.1 热力耦合控制方程

设材料为均质材料且各向同性，在三维空间域Ω⊂3中，不考虑阻尼的影响，材料热弹性动力学方程可表示为[11,15-16]

(1)

式中：ui表示位移向量分量，fi表示体积力分量，i=1,2,3;ρ为材料密度；t为时间；xj表示位置；σij为材料对称应力张量，j=1,2,3，工程上将分量排列写成向量形式

(2)

考虑热膨胀作用，材料总应变为

ε=εe+ε0

(3)

式中：ε0为温度应变；εe为弹性应变表达式。

材料应力与应变应具有如下本构关系

σ=Dεe=D(ε-ε0)

(4)

式中：D为本构矩阵，由材料Lamé常数λ与μ组成

(5)

考虑位移场对温度场影响，耦合热传导方程为

(6)

式中：θ=T-T0为温度增量，T为绝对温度值，T0为初始状态下的温度值；c表示材料比热；β为材料热模量，与材料热膨胀系数相关；k为材料热传导系数；εv=ε11+ε22+ε33为体积应变；h为热源项。

对于动力学方程，初始条件在区域Ω上的初始位移与初始速度为

(7)

对温度场，由于未知量选取的是温度增量，则初始温度增量为0，所以有

θ(x,0)=0

(8)

设物体的边界为光滑边界∂Ω，在位移场中，边界条件分为位移边界Γ1与力边界Γ2，在位移边界Γ1上给定位移值，一般取固定边界条件

u=0

(9)

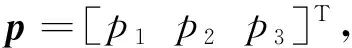
σijnj=pi

(10)

式中：nj为边界Γ2单元外法向向量分量。

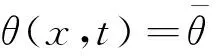
(11)

Γ′2上的热流为q，其边界条件为

(12)

由变分原理，将材料热弹性动力学方程与热传导方程分别乘以相应的测试函数，在空间Ω上积分，利用分部积分，并使用测试函数的性质，最终得到热力耦合方程弱形式如下

(13)

2.2 时间和空间离散

在区域Ω上进行网格剖分，离散成单元体Ω→ΣΩe，在整个有限元网格上将位移u(x,t)与温度增量θ(x,t)表示为节点的插值关系[11]，有

u=N(x)d(t),θ=X(x)ξ(t)

(14)

式中：d(t)为节点位移列阵；ξ(t)为节点温度增量列阵；N(x)与X(x)分别为位移场整体形状函数矩阵与温度场形状函数行向量。通过有限元单元分析与单元装配过程，最终得到通过空间离散热力耦合弱形式的方程组为

(15)

式中：Mu,Ku分别为结构场整体质量矩阵与刚度矩阵；Mθ,Kθ分别为温度场整体质量矩阵与刚度矩阵；L称为热力耦合矩阵；F与G分别为结构场与温度场的有限元右端项。

(16)

(17)

对于热弹性动力学方程，采用求解动力学方程中应用最为广泛的一种Newmark隐式方法来进行时间上的离散推进[17-18]，对于耦合热传导方程，使用求解热方程高精度Crank-Nicolson格式，最终可以统一写成矩阵形式为

(18)

式中：参数η∈[0,0.5]。

n+1时刻的加速度与速度由下列公式推导得

(19)

式中：参数ω∈[0,1]。

这是一般情况下热力耦合方程的时间推进计算格式，工程上称之为直接耦合法。根据本文研究问题的需要，可以采用变形不影响温度和不考虑弹性振动的顺序耦合形式，此时两方程也解耦，实际计算分别为

(20)

Kudn+1=Lξn+1+Fn+1

(21)

这是工程中便于使用的顺序耦合法，线弹性方程此时变成了静态问题。

2.3 导轨的热力耦合算法校验

为说明热力耦合算法的正确性，采用ABAQUS作为对比。验证过程既要可靠，又要便于实现。选用的材料与本文导轨一致,为7075航空铝，其T 73状态的相关系数如表1所示。

表1 7075航空铝热性能[19]Table 1 Thermodynamic properties of 7075 aviation aluminum[19]

采用本文中无振动顺序耦合法进行热力耦合分析，通过Fortran编程建立软件系统，其结构模块如图6所示，并以此实现模型的计算。

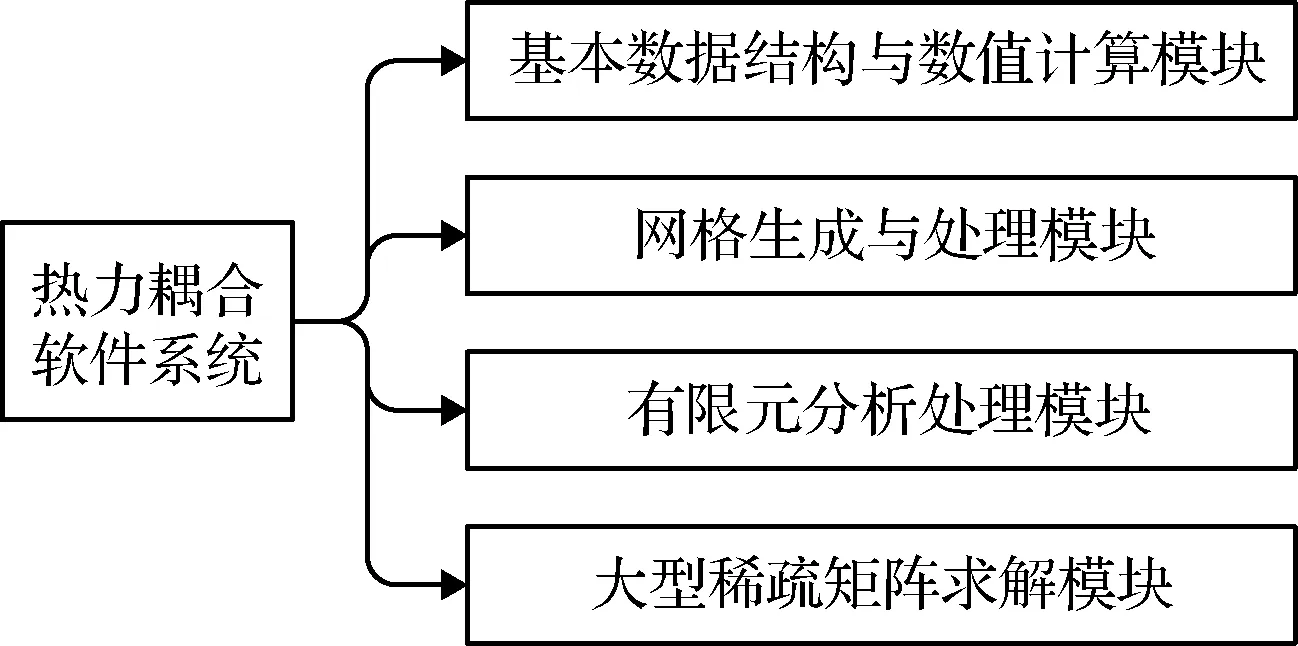
图6 热力耦合软件系统Fig.6 Thermo-mechanical coupling software system

算法的验证模型采用2mm×2mm×10 mm的实心长方体，如图7所示，固定其底面，环境温度为0 ℃，在一个侧面施加恒定温度100 ℃，采用线性四面体网格模型。另外采用ABAQUS进行对比验证，网格模型与边界条件同上，并进行计算。

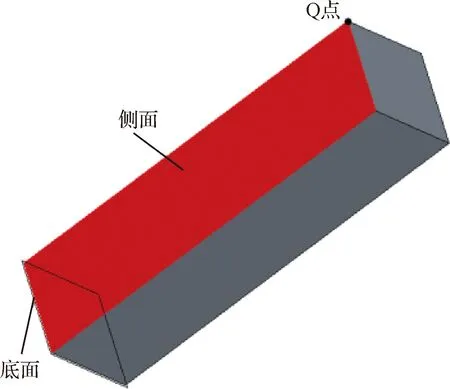
图7 长方体模型示意Fig.7 Cuboid model

从ABAQUS软件与本文算法自编程序中提取Q点的位移变化情况，Q点的位移对比结果如图8所示，程序计算与ABAQUS有一定的差异，不同数值方法计算的结果存在不完全一致的情况，但这不影响验证的准确性，该误差范围在数值验证上是可以接受的。对于这个问题的解析求解特别困难，所以在此采用不同的数值模型进行对比，说明本文建立的数值模型的可靠性，两种方法的结果曲线基本吻合,可说明本文采用的方法是有效的。

图8 Q点位移变化对比验证Fig.8 Comparison verification of the point Q displacement changes

太阳辐射是造成导轨温度升高的主要因素，以中国空间站为对象，假设其轨道高度保持400 km，为计算轨道周期，可采用开普勒第三定律[20]

(22)

式中：轨道半径r为6778.14 km，是地球赤道半径与轨道高度的和；引力常量G为6.67428×10-11N·m2/kg2；地球质量M为5.98×1024kg。由此可计算到中国空间站的轨道周期τ0为92.5 min。

假设导轨随空间站进行的是周期性规律转动，处于太阳辐射的半个周期为向阳面，另半个周期处于背阴面，如图9所示。根据受到太阳辐射强度不同，将导轨的正面与侧面区分开，如图9所示。导轨正面法向与太阳辐射的夹角为α，则有一个侧面法向与太阳辐射的夹角绝对值为(90°-|α|)，另一侧面不受辐射。为了简化运算，以空间站向阳面的最高温度Tmax=121 ℃为导轨的最高温度，背阴面Tmin=-157 ℃为导轨的最低温度。则一个轨道周期中导轨正面所受温度为

图9 太阳辐射角度Fig.9 Solar radiation angle

图10 导轨的正面与侧面Fig.10 The front and side of the guiding rail

(23)

导轨以图9中向阳面与背阴面的下交界点为起点进行顺时针运动，则太阳辐射角度随时间的变化关系为

(24)

根据式(24)的关系，一个轨道周期内导轨的正面与侧面的温度变化如图11所示，其中导轨的两个侧面采用一条虚线表示。

图11 导轨正面与侧面的温度变化Fig.11 Temperature change on the front and side of the guiding rail

导轨几何模型长1000 mm，宽170 mm，高90 mm，其有限元网格模型如图12所示，共含有3134个节点、11675个单元。采用的材料属性同表1。在图10所示位置固定导轨的底面，其余面自由。根据式(23)对正面与两个侧面分别施加温度，其中的两个侧面按照图9太阳辐射交替变化进行，同一时刻至多一个侧面直接接受太阳辐射，该过程为非稳态热力耦合计算。

图12 导轨的有限元网格模型Fig.12 Finite element mesh model of the guiding rail

在热力耦合响应计算过程中，后半个周期是处于背阴面,可视为稳态计算，为了减少运算量，从进入向阳面前的5 min开始计算，直到进入背阴面后的5 min停止。为减少两自由端对变形结果的影响，在导轨长度500 mm处取中间截面，如图13所示，其中的A点和B点可以代表导轨内侧面最大变形位置。

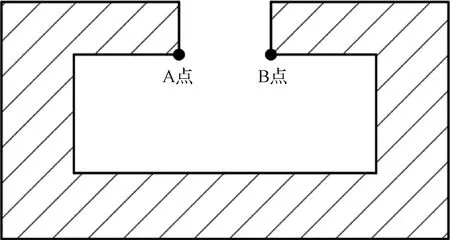
图13 初始时刻导轨形状Fig.13 Shape of the rail at the initial moment

计算后的位移变化结果分别如图14和图15所示，α=0°～180°为整个向阳面区间，背阴面部分没有太阳照射，所以这一段的值保持恒定。A点的极限位移为-0.2421 mm，B点的极限位移为-0.0388 mm。A点极限位移对应的导轨形状和截面温度分布分别如图16和图17，发生在导轨经过向阳面与背阴面的交界处，温度的突变会引起应变迅速增大，但明显小于导轨与牵引盘之间的侧面间隙(2 mm)和上下面间隙(3 mm)。因此，太阳热辐射引起的导轨形变不会影响牵引系统的正常工作。

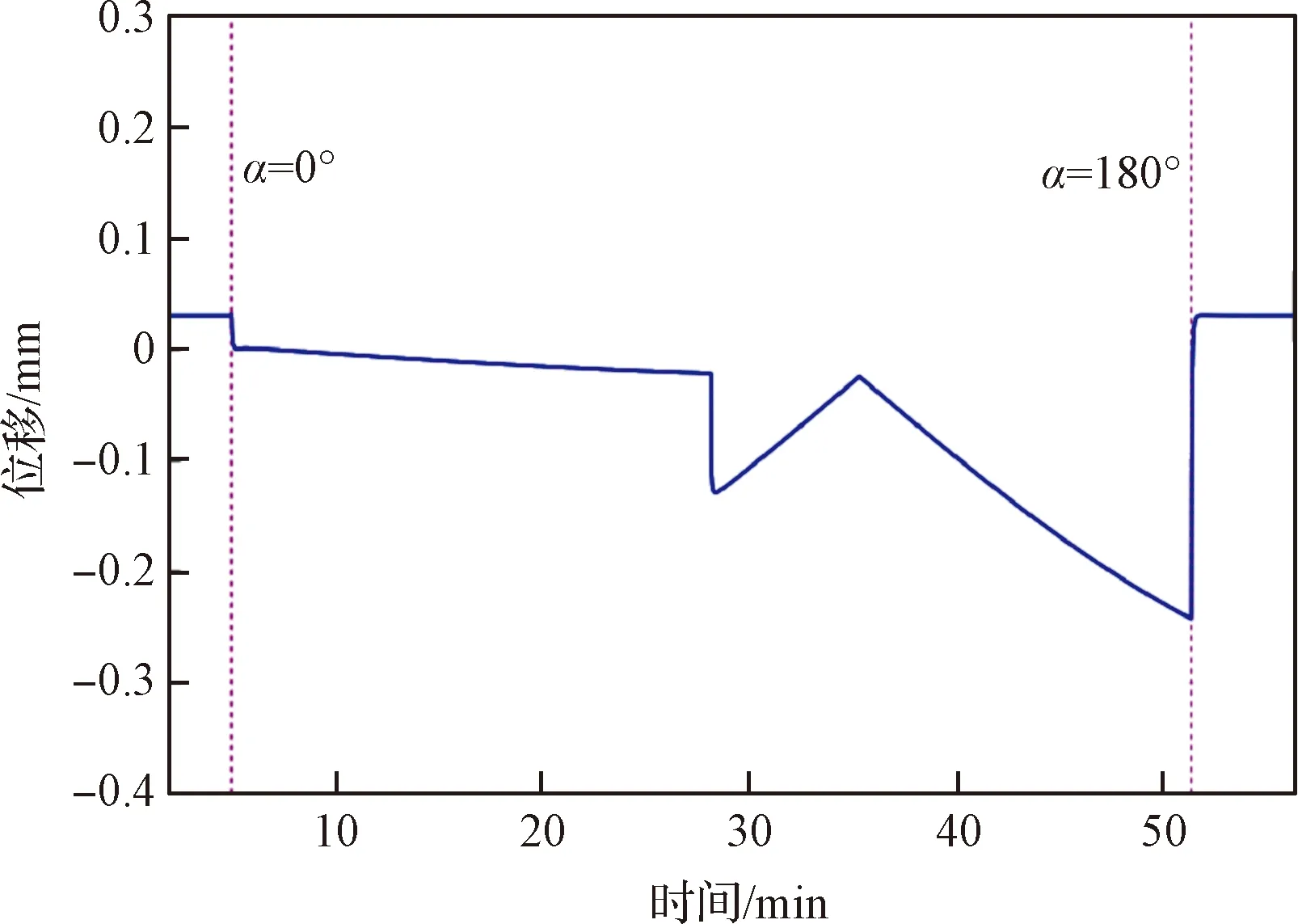
图14 A点随时间的位移Fig.14 Displacement of point A

图15 B点随时间的位移Fig.15 Displacement of point B

图16 A点最大位移时的导轨形状Fig.16 Shape of the rail at maximum displacement of point A

图17 A点最大位移时的截面温度分布Fig.17 Temperature distribution at maximum displacement of point A

3 牵引导轨结构强度校核与性能评估

3.1 牵引盘对导轨的作用力

为了对导轨的结构强度进行校核，首先要获得边界载荷，即计算出牵引盘与导轨之间的相互作用力。牵引盘在导轨中的位置如图18所示，考虑在极端工况下，牵引盘与导轨之间仅有三个接触点。

图18 牵引盘与导轨接触图示Fig.18 Contact points of the traction disk and the guiding rail

假设航天员连同舱外服的总重为190 kg，太空行走相对于舱体的最大速度为2 m/s，牵引绳绷紧时间为0.5 s，根据式(25)的动量定理，求得对牵引盘的拉力为760 N。

(25)

图19为图18的受力分析图，拉力F并不一直竖直向上，其方向与牵引盘径向所在平面的夹角为β，其中的F1,F2及F3分别为三个接触点的受力大小，为了模拟角度变化，以牵引盘中心为受力点，分别取β为90°,75°及60°。

图19 受力分析简图Fig.19 Brief diagram of force analysis

根据力学分析，三种情况下的计算结果如表2所示，即为静力学分析所需要的载荷大小。

表2 三种角度下的接触力大小Table 2 Contact force under different angles

3.2 结构强度校核与性能评估

表2的计算结果作为结构有限元分析的边界条件施加到导轨的相应位置，用于模拟极限条件下导轨的受力变形情况。在此采用ANSYS Workbench作为静力学计算工具，分别按照三种角度的受力大小和方向添加至导轨上。力的加载情况以及求解结果如图20所示，应力云图为受力点处截面，其显示效果在原变形上放大了6500倍。

图20 不同角度受力与对应的应力云图Fig.20 Stress contours of the guiding rail at different force direction

通过对三种情况的等效应力进行对比，75°受力下为最大值，发生在接触点1，其值为24.714 MPa，且与另外两种角度的等效应力相近。根据第四强度理论[21]，材料等效应力达到屈服应力即判定失效，参照GB/T3190—2020，7075航空铝的屈服强度为455 MPa，即在各种角度的受力情况下，舱外导轨仍满足强度要求，具备卓越的承载能力。

4 结 论

本文进行了空间站航天员出舱牵引系统的构型设计，可满足航天员在舱外任务时自主远距离移动，无需安全绳频繁锁挂，使舱外活动效率更高。通过热弹性动力学和热传导方程推导出结构热力响应数学模型，搭建了适于导轨热力耦合响应有限元算法软件系统，以此对牵引系统的导轨进行热力耦合分析，计算结果表明：在太阳辐射外热流作用下冷热交替引起导轨发生0.2421 mm的变形，小于最小间隙余量2 mm，不会对舱外作业造成影响。分析了极端工况下牵引盘对导轨的作用力，并进行静力学性能评估分析，结果表明：导轨上的最大应力为24.714 MPa，远小于7075航空铝的屈服应力，得以满足结构强度使用需求。提供了一种航天员出舱牵引系统构型设计与结构响应有限元算法性能评估方法，后续有待进一步深化研究。