空间机器人神经网络自适应滑模目标操控轨迹跟踪控制

王 嵩，王蜀泉，张 龙

(1. 中国科学院太空应用重点实验室, 中国科学院空间应用工程与技术中心，北京 100094； 2. 中国科学院大学，北京 100049)

0 引 言

随着航天技术不断发展，为了确保航天器稳定高效地在轨运行，保证航天器的工作寿命，需要对航天器及其所处的轨道空间进行有效服务。其中包括对在轨航天器进行修理维护、失效航天器清除、空间碎片清除，辅助完成空间任务等。采用空间机器人系统执行相关的工作是完成这些任务的可行方案之一，通过在轨空间机器人系统进行目标操控可以有效地实现失控航天器的维护以及捕获因多种因素产生且散布在轨道空间的垃圾碎片等任务。

微重力环境下在轨的空间机器人是一个动力学高度耦合的系统，一般由两部分组成，飞行基座平台以及固定在基座上的机械臂。机械臂的运动会对飞行基座平台的位姿产生直接的影响。同时空间机器人系统在工作中也会存在不确定的动力学参数以及不确定的系统干扰等，其中包括基座燃料消耗和操控目标所带来整体系统质量、转动惯量的变化，也包括系统未建模动态所带来的动力学不确定性，以及系统存在摩擦等扰动，这些不确定性和未知扰动大大增加了空间机器人的控制难度。在空间机器人存在动力学不确定性和扰动的情况下，为确保系统飞行基座姿态的稳定，实现机器人对期望轨迹的准确跟踪，探究空间机器人系统的自适应稳定控制是十分必要的。

针对空间机器人的控制问题已有大量的研究，空间机器人系统作为一个高度非线性、强耦合的系统，相关研究人员已经采用许多方法去实现系统的稳定控制，如自适应控制[1-3]、神经网络控制[4-6]、滑模变结构控制[7-9]以及多种方法结合等。文献[10]结合PID控制与递归神经网络，在完全无需系统动力学模型的条件下，实现机械臂轨迹跟踪，但在关节角速度偏大时，跟踪误差也显著增大。文献[11]提出了一种基于模糊自适应扰动观测器的鲁棒控制方案，不需要系统精确模型即可实现稳定的跟踪控制，当存在扰动时，其输出力矩存在频率较高的切换。文献[12]结合障碍李雅普诺夫函数和径向基(Radial basis function，RBF)神经网络设计输出反馈控制器，实现自由飞行空间机器人系统在状态性能受限下的跟踪控制，具有较好的自适应性和鲁棒性。文献[13]考虑空间机器人的柔性多体动力学，结合RBF-BP神经网络与自适应控制器，在系统存在振动的情况下实现较好的稳定控制，但神经网络对逆动力学的拟合需要预先训练，缺乏实时的自适应性。文献[14]针对扰动以及惯性不确定性，提出了结合扰动观测器、给定性能H_∞控制以及迭代学习控制(ILC)的方案，使机械臂具有良好的轨迹跟踪性能，但ILC作为补偿器，仅在重复性任务中才具备良好的瞬态特性。文献[15]则将非线性模型预测控制应用于自由漂浮空间机器人系统中，在系统参数不完备且具有扰动的情况下仍能实现最优轨迹的跟踪。文献[16]提出一种结合标称SDRE(State-dependent riccati equation)控制器和补偿SDRE控制器的方法，在惯性参数不确定的情况下实现末端轨迹的有效跟踪，但跟踪性能仍有提升空间。文献[17]提出基于时延估计的无模型控制方法，有着较优的跟踪控制效果，然而此方法对时延估计误差未进行较好的鲁棒处理。文献[18]针对连续型空间机器人位姿与形态控制基于阻尼配置-无源性控制设计控制器，通过非线性干扰观测器对外部干扰进行补偿，具有一定的鲁棒性。文献[19]将RBF神经网络应用到空间机器人无传感器阻抗控制，实现动力学模型不确定下接触力的估计补偿。

滑模控制因其变结构特性而具有良好的鲁棒性，是处理系统不确定性和外部扰动十分有效的控制方法，在航天器[20]、超高声速飞行器[21]、地基机器人系统[22-23]等多领域均有应用。传统的线性滑模控制能够实现系统状态的渐近稳定，却并不能使状态在有限时间内收敛到零，采用终端滑模则能够克服此问题，然而终端滑模存在奇异问题，可设计连续分段的滑动模态进行切换以规避奇异[24]。同时，由于滑模变结构控制中切换项的存在，控制输入会产生高频抖振现象，这会对系统实际的物理执行机构产生严重的不利影响，文献[25]提出一种自适应积分滑模控制器，在执行机构输出受限制的情况下，实现空间机器人有限时间内轨迹跟踪控制，且无高频抖振的产生，但在积分滑模初始误差较大的情况下会导致较长的调节时间。文献[26-27]提出了RBF神经网络与传统线性滑模结合的方法，神经网络对自由漂浮空间机器人模型不确定因素进行逼近。此方法并未考虑RBF神经网络对高自由度空间机器人动力学逼近时误差变化带来的对滑模控制器参数自适应的要求。

本文针对空间机器人动力学模型存在不确定性和系统扰动下关节轨迹跟踪的稳定控制问题进行研究，利用RBF神经网络估计系统动力学模型中的不确性项，由此设计一种自适应增益的非奇异终端滑模控制器，在扰动上界未知的情况下可实现空间机器人系统基座姿态的稳定控制和机械臂关节对期望轨迹的快速稳定跟踪。

1 动力学模型

本文针对空间机器人抓取非合作目标过程中动力学模型发生未知变化以及存在其它扰动情况下的轨迹跟踪控制问题进行研究。动力学模型发生的未知变化会引起用于控制律的计算出现不确定的误差，因此所设计的控制算法需要具有较强的鲁棒性和自适应性。

一般而言，空间机器人是由一个飞行基座与多个自由度的机械臂连接而成的组合体。针对相关问题的研究，本文有下几点假设：

假设 1.空间机器人系统为刚体组合，不考虑系统中的柔性部分；

假设 2.忽略重力梯度对空间机器人系统的影响；

假设 3.空间机器人系统初始的线动量和角动量均为零。

空间机器人系统模型如图1，飞行基座具有3个平动自由度和3个转动自由度，机械臂可视为由n个关节及其连杆组成，则空间机器人系统共有6+n个自由度。

图1 空间机器人系统模型Fig.1 System model of a space robot

从基座开始对飞行基座以及连杆依次标记为0,1,2,…,n, ∑I表示惯性系，∑0为飞行基座本体系，Σi为固连在关节上的关节坐标系。

Ji(i=1,2,3,…,n)表示空间机器人机械臂关节i,ai∈R3(i=1,2,3,…,n)表示关节i指向连杆质心Ci的向量，bi∈R3(i=1,2,3,…,n)表示连杆质心Ci指向关节Ji+1的向量。ki∈R3(i=1,2,3,…,n)为关节i旋转方向的单位矢量，ri∈R3(i=0,1,2,…,n)为刚体i质心的位置矢量，为惯性系到刚体质心的位置矢量。pi∈R3(i=1,2,3,…,n)为关节i的位置矢量。

空间机器人系统的总动能则为：

(1)

式中：ωi∈R3为第i个刚体的角速度；mi∈R为第i个刚体的质量；Ii∈R3×3第i个刚体的绕其质心的惯量矩阵。

机械臂连杆的角速度和质心的速度和分别为式(2)和式(3)：

(2)

(3)

式中：v0∈R3为基座的线速度；ω0∈R3为基座的角速度；θj∈R为关节j旋转角度。将式(2)和式(3)代入式(1)，得到由基座速度、角速度以及机械臂关节角变化率表达的系统总动能：

(4)

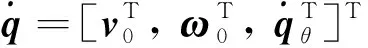
由假设2忽略重力梯度的影响，可取系统整体的势能为0。应用第二类拉格朗日方程：

(5)

由式(5)可得到空间机器人系统的动力学模型：

(6)

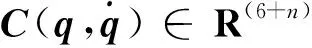
(7)

考虑机械臂的运动给飞行基座带来作用力和力矩，为保证基座稳定，对基座姿态和机械臂运动均进行主动控制。在空间机器人系统的工作中，系统实际的动力学参数与标称系统参数因未建模动态和燃料消耗等影响并不完全相同。机械臂末端抓取动力学参数未知的负载之后，系统实际的动力学参数也会产生改变。此外，系统还会受到挠性等引起的扰动。综合考虑各类不确定性，空间机器人系统的动力学方程建立为：

(8)

式中：τ∈R3+n为姿态与关节的控制力矩；H0∈R(3+n)×(3+n)表示标称广义惯性张量；ΔH∈R(3+n)×(3+n)表示广义惯性不定项；C0∈R3+n表示科氏力、离心力等非线性标称项；ΔC∈R3+n表示非线性不定项；d∈R3+n表示系统扰动。

考虑到实际空间机器人系统的特点，本文假设不确定项以及系统扰动为时变且存在上界的。为实现空间机器人工作空间内的稳定操控，对不确定项进行估计以便克服不确定项与外部扰动的影响。

由式(8)，系统的动力学方程表示为：

(9)

(10)

(11)

式中：

(12)

(13)

结合式(1)～(13)，系统动力学模型表示为：

(14)

式(14)包含所有不确定项以及系统扰动，控制力对系统的作用不仅受广义惯性张量的影响，还受到时变JE的影响，系统具有较强的非线性。

2 控制器设计

滑模变结构控制具有良好的鲁棒性，可以迫使状态轨迹在有限时间内到达滑动流形，并使其保持在滑动流形上，最终使系统状态收敛到平衡点。此方法需要知道不确定项和扰动的上界。通常会较为保守的设置较大的增益以保证鲁棒性，而当增益较大时，控制输入会出现较大的抖振。另一方面，当不确定性和扰动出现较大变化使其上界超出所设增益时，此时控制器需要更改鲁棒项的增益参数。

因此，在模型存在较大不确定项的情况下，控制器需要具有一定的鲁棒性和自适应能力，在确保稳定的前提下获得较好的控制性能。为减小不确定性的影响，本文采用神经网络对不确定项进行估计，在控制中对不确定项进行前馈补偿，以降低抖振和不确定项对增益的要求。同时采用自适应控制方法驱动系统状态收敛到滑模面，此处自适应控制可以克服神经网络不确定项估计误差带来的影响。

针对空间机器人这类强非线性的系统，为克服系统的不确性和扰动，设计基于神经网络及自适应增益终端滑模控制器，其系统框图如图2所示

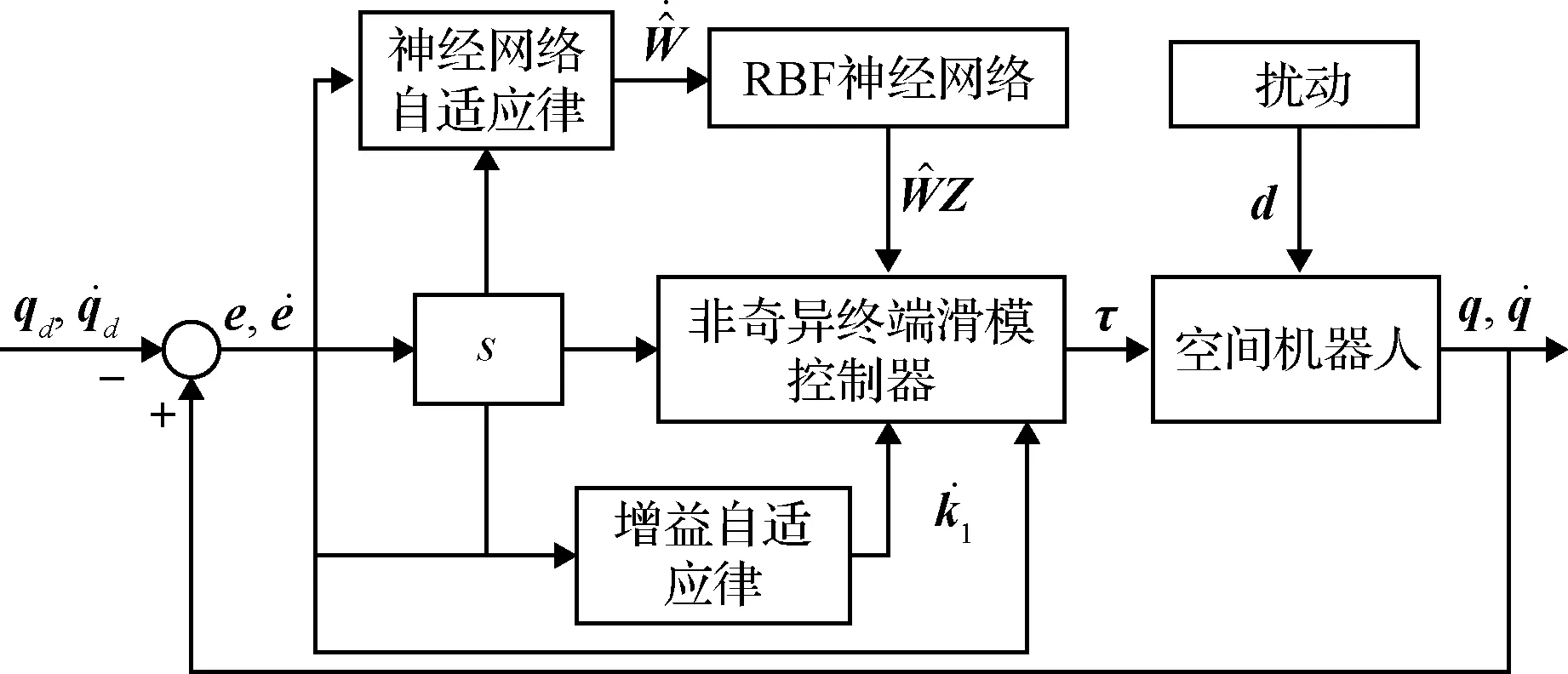
图2 控制系统组成Fig.2 Composition of the control system

2.1 径向基神经网络估计

考虑动力学模型中的不确定项，采用神经网络对其进行拟合估计，将所有不确定项记为f(x)，则有：

(15)

径向基神经网络对非线性函数有着十分良好的拟合效果，对于连续的非线性函数f*(x):Rk→Rm，理想的网络逼近如式：

f*(x)=W*TZ(x)+ε*

(16)

式中：W*∈Rk×m为最优的权重矩阵；ε*∈Rm为最优估计误差Z(x)=[Z1(x),Z2(x),…,Zk(x)]T为RBF基向量，其中：

(17)

在最优估计下f(x)=f*(x)。由于理想的权重矩阵W*是未知的，在实际控制过程中需要对其进行估计，表示如式：

(18)

定义神经网络权重估计误差：

(19)

则对不确定项f(x)的估计误差ε表示为：

(20)

结合式(14)和式(15)则有：

(21)

径向基神经网络需对f进行估计。

2.2 自适应增益滑模变结构控制器

定义非奇异终端滑模面：

(22)

(23)

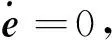
针对空间机器人系统设计如下控制律：

τ=τ1+τ2

(24)

(25)

τ2=-H0JE(ΛS+diag(k0+k1)sgn(S))

(26)

式中：Λ∈R(3+n)×(3+n)为正定对角矩阵；k0∈R3+n和k1∈R3+n为切换项增益，其中k1为自适应增益。

对于整个闭环系统而言，RBF神经网络对未知项的估计存在误差，为了保证控制器的鲁棒性和快速响应，在一般情况下，切换项增益k0的设置会偏保守进而设置较大，而较大的增益会增大抖振的幅度，对执行机构产生不利影响；若所设置的切换项增益k0小于总的误差ε的上界，那么闭环系统的稳定性会受到直接影响。为保证系统鲁棒性的同时避免出现切换项增益过大，本文增加自适应增益k1，受文献[28]启发，设计自适应律：

(27)

式中：η>0为自适应调整率。

设计神经网络自适应律：

(28)

式中：ζ∈R(3+n)×(3+n)为正定对角矩阵，表示神经网络学习率。

将式(16)、(18)、(21)和式(24)～(26)代入式(23)则有：

ΛS-diag(k0+k1)sgn(S)]

(29)

3 控制系统稳定性证明

定理 1.对于式(21)描述的空间机器人系统，式(24)～(26)所示的控制律以及式(27)、(28)所示的自适应律，能够保证系统跟踪误差e在有限时间t内收敛到0。

证.令ε0为神经网络估计误差上界|ε|≤ε0，定义

(30)

考虑到：

(31)

式中：tr(*)表示矩阵的迹。

将式(31)代入式(30)，并对时间求导则有：

(32)

将式(19)和式(29)代入式(32)则有：

(33)

(34)

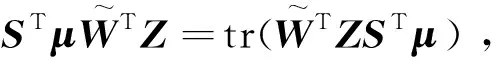
STμ[-ΛS-diag(k0+k1)sgn(S)+ε*]+

(35)

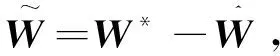
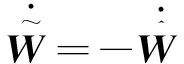
(36)

将自适应律(28)和式(36)代入式(35)可以得到

(37)

diag(k0+k1)sgn(S)+ε*]-|ST|μ(ε0-k1)≤

-STμdiag(k0+k1)sgn(S)+STμε*-

|ST|μ(ε0-k1)

(38)

式中: |ST|表示对列矩降中每个元素取绝对值。

由于STμdiag(k0+k1)sgn(S)=|ST|μ(k0+k1)，将其代入(38)有：

-|ST|μk1+STμε-|ST|μ(ε0-k1)≤

|ST|μ|ε|-|ST|με0≤-|ST|μ(ε0-|ε|)

(39)

证明S在有限时间内收敛到0，定义候选李雅普诺夫函数：

(40)

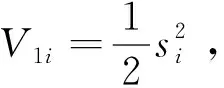
STμε-STμΛS-STμdiag(k0+k1)sgn(S)≤

|ST|μ|ε0|-|ST|μ(k0+k1)-STμΛS≤

-STμΛS-|ST|μ(k0+k1-|ε0|)

(41)

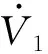
(42)

(43)

考虑单个控制通道，不等式(44)同成立：

(44)

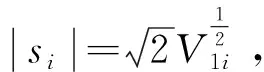
(45)

(46)

其中,V(x0)为李雅普诺夫函数初始值。

由引理1，非奇异终端滑模si将在有限时间内收敛到零，收敛时间为：

(47)

当状态到达滑模面后，即si=0，由式(16)有：

(48)

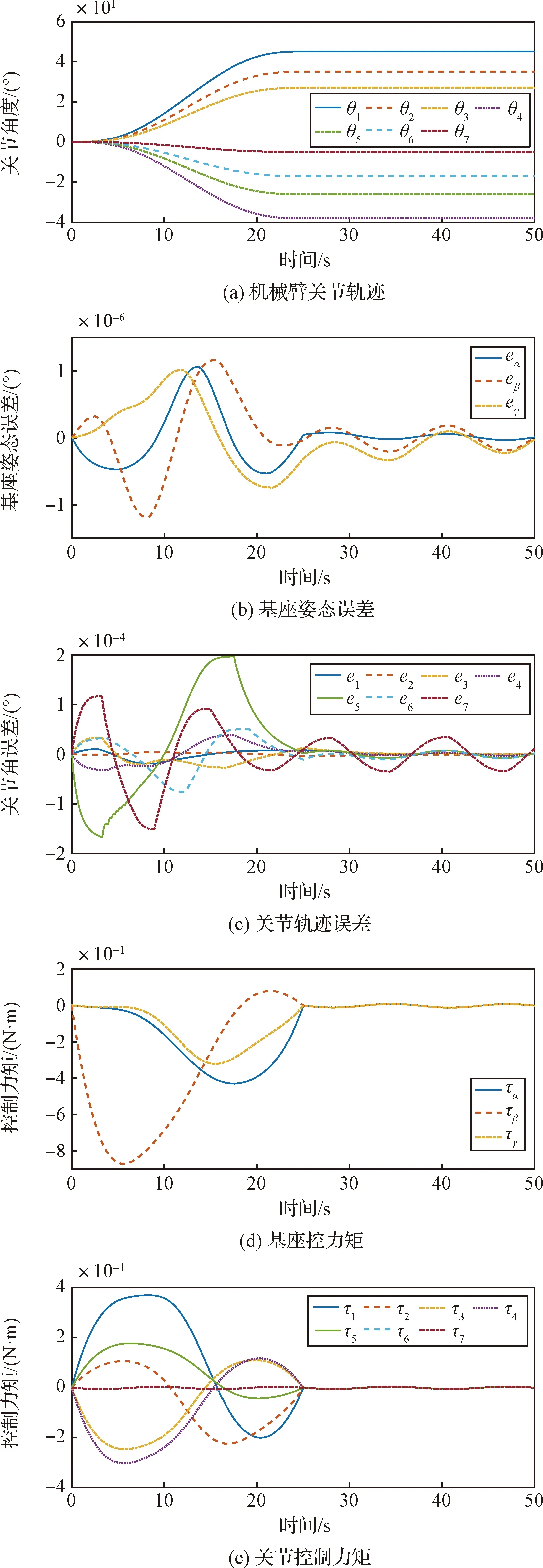
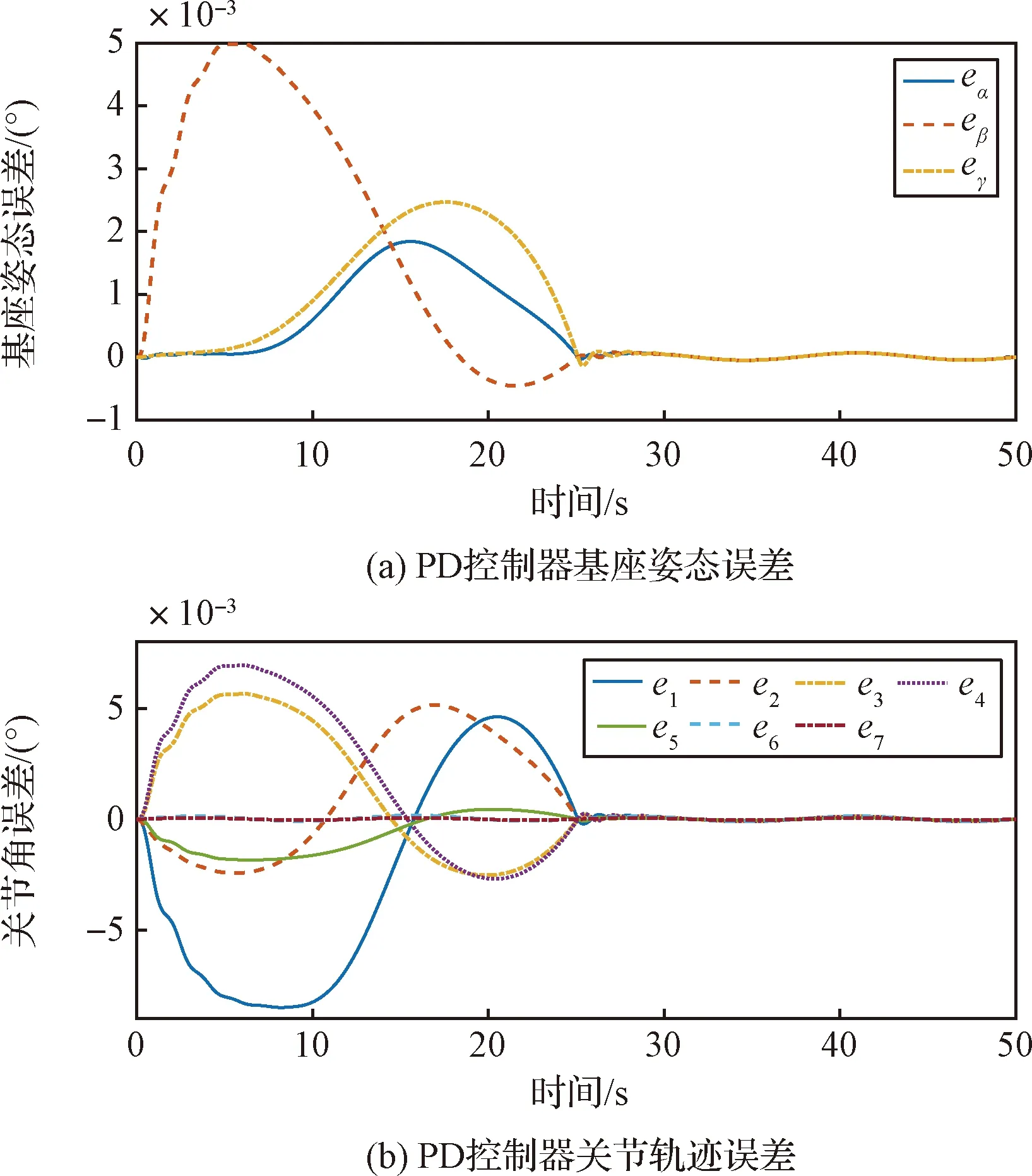
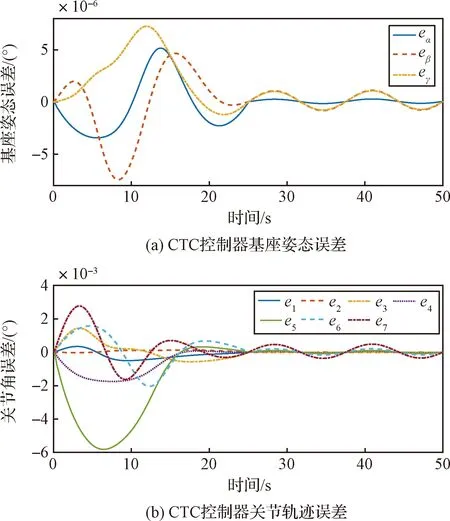
在t

不连续的切换控制为带来抖振问题，为避免对物理执行机构造成不良影响，使用双曲正切函数替换符号函数，双曲正切函数为：

(49)

最终控制律设计为：

(50)

4 仿真校验

表1 空间机器人动力学参数Table 1 Dynamics parameters of the space robot

表2 机械臂D-H参数Table 2 D-H parameters of the space robot

控制器参数设置如表3所示。为进一步验证所设计控制算法的有效性，本文将所设计的控制算法与PD(Proportional derivative control)算法、计算力矩法(Computed torque control，CTC)[30]和无神经网络前馈和增益自适应的非奇异终端滑模控制(Non-singular terminal sliding mode control，NTSMC)[31]进行比较。PD控制增益参数设置为：

表3 控制器参数Table 3 Parameters of the controller

Kp=[10,10,10,2.5,2.5,2.5,2.5,5.5,

2.5,5.5]T×103

Kd=[8,8,8,2,2,2,2,2,2,4]T×102

CTC控制增益参数与PD控制相同。NTMSC控制律如式(51)，其控制参数与本文控制器滑模参数相同。

(51)

空间机器人系统初始的基座姿态与关节角度设置为q0=[0,0,0,0,0,0,0,0,0,0]T，基座姿态的期望控制目标以及关节角的期望控制目标设置为qf=[0,0,0,45°,35°,27°,-38°,-26°,-17°,-5°]T。

为验证关节轨迹跟踪控制效果，仿真中采用五次多项式插值对机械臂关节运动轨迹进行规划，规划所得运动轨迹作为控制参考轨迹，如式(52)所示：

qd=a0+a1t+a2t2+a3t3+a4t4+a5t5

(52)

4.1 算例1

空间目标操控下系统动力学不确定性的主要来源为机械臂末端的未知目标负载以及存在的系统扰动，仿真中设置负载的动力学参数如表1末行所示，设空间机器人飞行基座受到的系统扰动力矩为：

dα=dγ=dβ=0.01sin(0.5t)+0.005sin(0.01t)

(53)

设机械臂各转动关节所受到的扰动力矩均为：

dθi=0.004sin(0.5t)+0.002sin(0.01t)

(54)

则系统扰动d可表示为：

d=[dα,dβ,dα,dθ1,dθ2,dθ3,dθ4,dθ5,dθ6,dθ7]T

(55)

未知负载和扰动所引起的空间机器人系统的动力学变化对控制器而言是时变的未知量，其仿真结果如图3～6所示。

图3 控制器效果Fig.3 Effects of theproposed controller

图4 PD控制器基座姿态与关节轨迹误差Fig.4 Attitude of the base and the joints trajectory errors of the PD controller

图5 CTC控制器基座姿态与关节轨迹误差Fig.5 Attitude of the base and the joints trajectory errors of CTC controller

图6 NTSMC控制器基座姿态与关节轨迹误差Fig.6 Attitude of the base and the joints trajectory errors of the NTSMC controller

从图3可知本文所设计的控制器能够实现机械臂对期望轨迹的快速稳定跟踪并保持基座姿态的稳定。关节7受到末端未知负载影响，当到达期望角度后在扰动力矩的影响下其误差最大；关节5运动过程中非线性力更大，因此跟踪过程角度误差最大。

在此算例中，本文提出的算法同图4～6所示的结果比较，其基座姿态误差在机械臂的运动阶段均不大于1.3×10-6度，在机械臂姿态维持阶段为1×10-7角度量级，均小于PD、CTC和NTSM控制算法下的误差，即所提算法在基座姿态控制精度上具有显著优势。对于机械臂关节轨迹的跟踪控制，本文提出的算法其跟踪误差为1×10-5～2×10-4角度量级，小于PD、CTC算法的1×10-4～8×10-3角度跟踪误差。NTSMC在关节5上最大误差超过0.4°，本文所提算法控制误差也远小于NTSMC的误差，在机械臂关节运动控制上具有更好的准确性，其优势来源于RBF神经网络对系统不确定的总体估计与补偿以及自适应滑模增益确保系统状态在全局的稳定性。

4.2 算例2

为进一步验证算法的鲁棒性和自适应性，控制器参数不变，系统扰动幅值增大到算例1中的10倍，同时机械臂末端未知负载的质量大小设为算例1中的2倍。飞行基座和关节所受到的扰动为：

dα=dγ=dγ=0.1sin(0.5t)+0.05sin(0.01t)

(56)

dθi=0.05sin(0.5t)+0.02sin(0.01t)

(57)

仿真结果如图7～10所示。

图9 CTC控制器基座姿态与关节轨迹跟踪误差Fig.9 Attitude of the base and the joints trajectory errors of the CTC controller

图10 NTSMC控制器基座姿态与关节轨迹跟踪误差Fig.10 Attitude of the base and the joints trajectoryerrors of the NTSMC controller

从图7可知，在系统扰动以及动力学不确定性增大时，本文所设计的控制器依旧能够实现机械臂对期望轨迹跟踪控制和基座姿态的稳定。此算例下，本文提出的算法同图8～10所示的结果比较，其算法基座控制误差最大在5×10-6角度量级，相较于PD控制的8×10-3度和CTC、NTSMC控制2×10-5度仍具有明显优势。机械臂关节角度跟踪误差最大在9×10-4度，优于CTC和PD算法。此时在较大的系统不确定下，NTSMC控制下的空间机器人最大关节角误差超过40°，关节5～7误差太大，已无法准确跟踪期望轨迹。

同算例1相比，四种控制算法其控制误差均增大，但本文所提算法控制误差增大的绝对值最小，而无神经网络自适应和增益自适应的NTSMC控制，已无法快速准确的跟踪机械臂关节期望轨迹。本文所提出算法具有较好的鲁棒性和自适应性。空间机器人系统动力学模型存在不确定以及存在系统扰动的情况下，本文所设计的控制器具有较好的运动控制准确性以及较好的稳定性。

5 结 论

本文针对非合作目标操控任务中空间机器人系统动力学系统参数存在未知变化和系统扰动的问题，提出一种基于径向基神经网络及自适应增益的非奇异终端滑模控制器，实现对较大不确定性操控任务场景的运动轨迹稳定跟踪。采用径向基神经网络对系统动力学的不确定项进行估计，并通过自适应增益去克服系统总扰动以及神经网络估计的误差。采用李雅普诺夫稳定性理论对控制器的闭环稳定进行了证明，最后通过数值仿真对控制算法进行验证。

其仿真结果表明，在系统动力学存在不确定性和系统总扰动未知的情况下，所提出的控制器并不需要精确模型以及先验的扰动上界，即可使空间机器人基座稳定并能实现对期望轨迹快速且精确的跟踪，且最终闭环系统具有良好的鲁棒性。

本文自适应增益会随着误差的存在而一直增大，虽增大的速率较慢，但仍需要考虑到实际物理执行机构的饱和特性以及增益动态调度需求。