灵活运用函数的单调性处理不等式问题

洪昌强

(浙江省台州市第一中学 318000)

函数的单调性是函数的重要性质之一，在研究比较大小时发挥了重要作用.但在解决一些稍为复杂或者含有多变量不等式问题时，若生搬硬套直接使用单调性去处理不等式问题，往往会束手无策，感觉无能为力.正确的思路是需要对不等式或函数先进行适当变形、变更主元、重构函数、变换问题的角度，然后再利用函数的单调性进行解决.如何灵活运用函数的单调性处理不等式问题呢？下面举例介绍.

1 变更主元

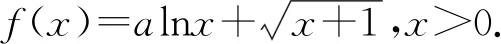
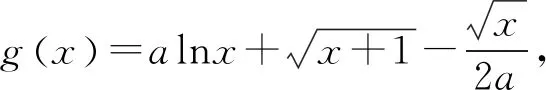
由题意知a>0，解关于a的二次方程

所得的式子较复杂，要确定a的范围更为困难.绝大多数学生的解题思路在此受阻、中断.其实此题需要逆向思维，重新审视题目中信息，调整思维，改变解题思路.

首先从特殊情况出发， 由题意，得

评注此题以函数、不等式等核心知识为背景，是不等式恒成立条件下求参数范围问题.本题通过变换主元，将不等式恒成立问题化归为二次不等式恒成立问题，然后使用单调性进行处理.需要解题者用批判性思维审视问题，破解新情境对问题的迷惑.此题不仅考查了数学基本知识和基本技能，还重点考查了考生的灵活应变的能力和自我调控能力.

2 重构函数

例2 (2020年山东新高考第22题第(2)问)已知函数f(x)=aex-1-lnx+lna．若f(x)≥1，求a的取值范围．

分析本题若从f(x)的最小值入手，需要知道f(x)=aex-1-lnx+lna的单调性，但f(x)的单调性不明显.能否调整原来的函数式，重构新的函数？

仔细观察f(x)式子的结构特征，不难发现

aex-1-lnx+lna=elna+x-1-lnx+lna，

即f(x)≥1等价于

elna+x-1+lna+x-1≥lnx+x=elnx+lnx.

设g(x)=ex+x,则上式不等式等价于

g(lna+x-1)≥g(lnx).

易知g(x)是单调递增函数.

所以lna+x-1≥lnx.

即lna≥lnx-x+1恒成立.

下面只需求函数h(x)=lnx-x+1的最大值.利用导数易求h(x)最大值为0，所以a≥1.

评注此法对代数式运算能力要求较高，正如章建跃博士所说：推理是数学的命根子，运算是数学的童子功.通过调整原函数的结构，重新建构一个“好”的函数，单调性发挥其应有的作用，使问题起死回生.

3 变换问题

(1)若f(x)在x=x1，x2(x1≠x2)处导数相等，证明：f(x1)+f(x2)>8-8ln2；

(2)若a≤3-4ln2，证明：对于任意k>0，直线y=kx+a与曲线y=f(x)有唯一公共点．

因为x1≠x2，再由基本不等式，得x1x2>256．

所以g(x)在(16，+∞)上单调递增.

故g(x1x2)>g(256)=8-8ln2.

即f(x1)+f(x2)>8-8ln2．

所以对于任意k∈(0,+∞)，直线y=kx+a与曲线y=f(x)有唯一公共点.

评注一些不等式证明以及研究方程解的个数和解的范围问题，若从函数的目光去审视，可将方程问题化归为函数问题进行处理，然后结合函数的单调性，问题一蹴而就.同时，也表明函数、不等式、方程三者之间密切相关，相互之间互为转化.

分析由f′(x)=ex-b=0,得x=lnb.

所以f(x)在(0，lnb]上单调递减，在(lnb，+∞)上单调递增.

因为b>e4，则极小值f(lnb)=b-blnb+e2<0.

结合图1，直观猜测x1<2.

事实上，易证f(2)<0.

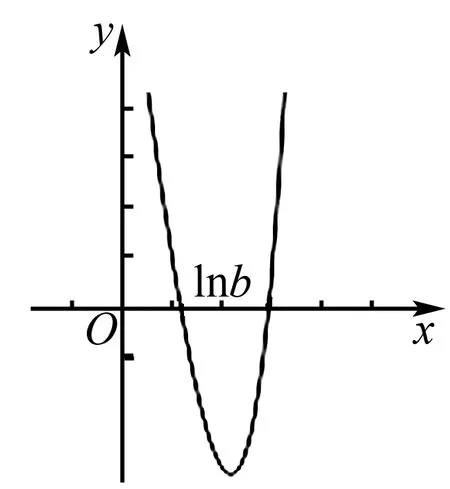
图1

通过对零点x1放缩处理，将含2个零点的不等关系问题,转化为只含一个零点的范围证明.

再由函数的单调性知，即证

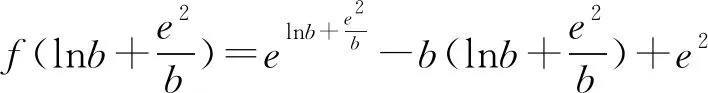
且b>e4，

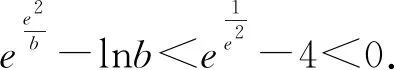
评注此题的处理方法充分利用了函数单调性的特有功能，比较变量大小问题与比较函数值大小问题可以进行互化.此法利用函数单调性先得一个零点x1<2，然后通过放缩变换，将原不等式中含2个零点不等关系问题转化为一个零点的范围问题，再利用函数的单调性，将函数零点大小问题化归为函数值符号问题.一些函数的零点往往较难求出，它们零点之间的不等关系问题，常常通过函数的单调性转化为函数值大小问题进行处理.处理函数的单调性常用方法有观察法、定义法、导数法，其中导数是研究函数单调性的重要工具.