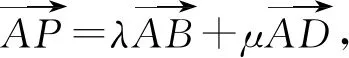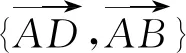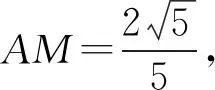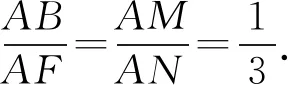等和线的深入研究
2023-03-18程志松
程志松
(山东省宁阳县第一中学 271400)
在同一平面中相交于原点的两条数轴,如果它们的度量单位相等,称为笛卡尔坐标系,其中两条数轴互相垂直的笛卡尔坐标系,称为笛卡尔直角坐标系,否则称为笛卡尔斜角坐标系.笛卡尔平面直角坐标系是我们平时使用最多的坐标系.那么若两数轴的度量单位不一定相等时就构成了平面仿射坐标系.仿射变换是一种线性变换,能够保持图象的平行性与平直性,借助仿射变换这一特点,我们可以构建仿射坐标系.
已知向量a,b不共线,令a方向为x轴正方向,b方向为y轴正方向,如图1建立仿射坐标系.

图1

仿射坐标系同样拥有四个象限,其坐标符号与平面直角坐标系一样,第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-).
我们首先研究一下在笛卡尔平面直角坐标系中直线方程截距式在向量基底作用下的几何意义.
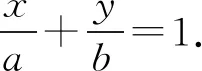
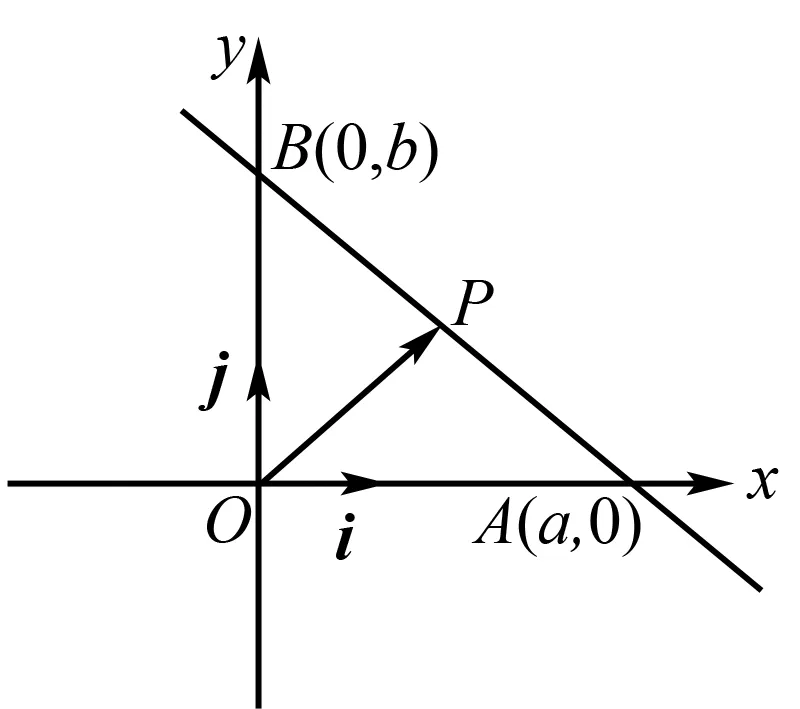
图2
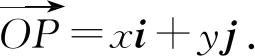

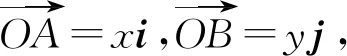
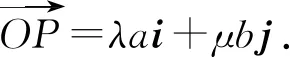
所以x=λa,y=μb.

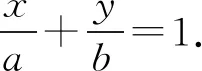
通过分析发现,基底作用下向量表示与直线方程的截距式是等价的.那么在仿射坐标系中,我们能否得到相同的结论呢?
如图3,{m,n}为仿射坐标系下的一组基底.
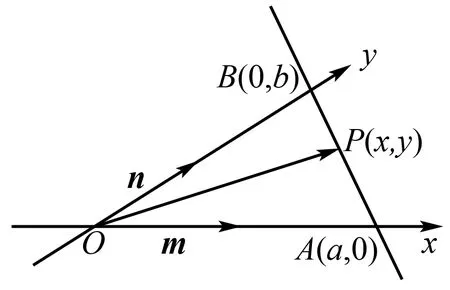
图3

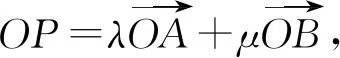
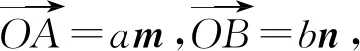
则OP=λam+μbn.
所以x=λa,y=μb.

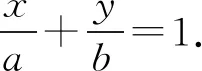
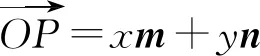
下面我们以高考题为例,浅析等和线的应用.
1 等和线求取值范围


由题意可知P(x,y)在第二象限,所以x<0.
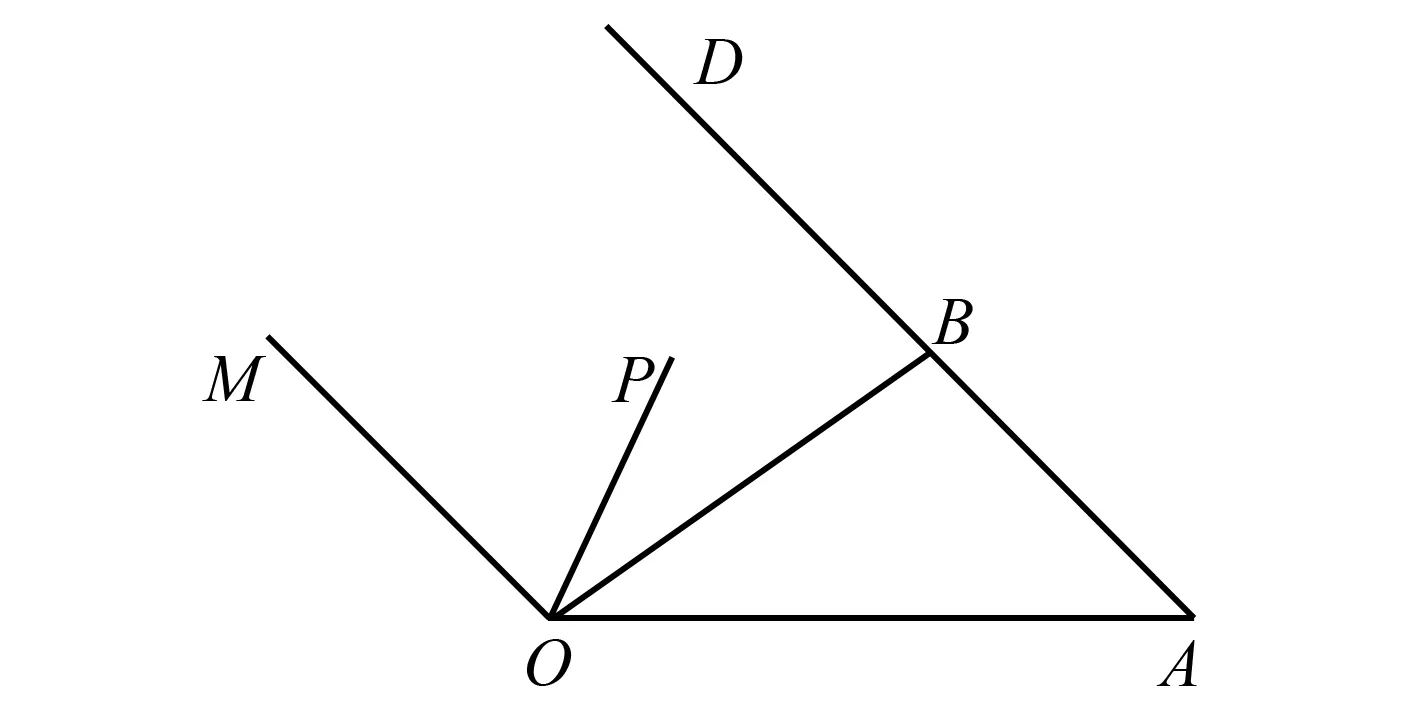
图4

图5
由等和线可得直线OB为x+y=1,直线OM为x+y=0.
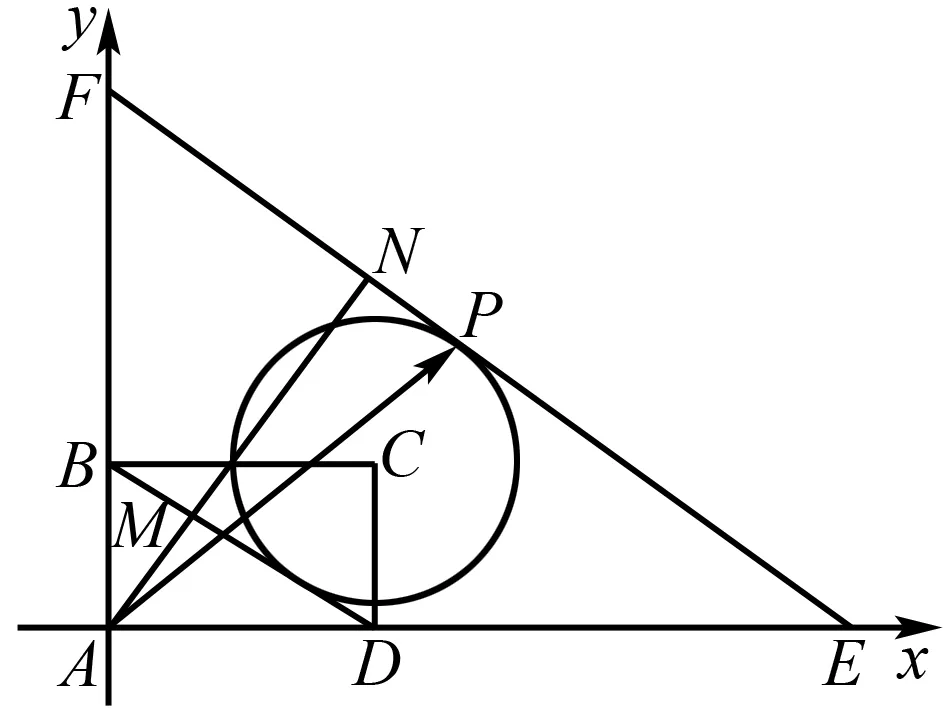
因为点P在由射线OM,线段OB及AB的延长线围成的区域内(不含边界),所以0 图6 因为|λ|+|μ|≤1, 所以λ>0,μ>0时,λ+μ≤1; λ<0,μ>0时,-λ+μ≤1; λ<0,μ<0时,-λ-μ≤1; λ>0,μ<0时,λ-μ≤1. 图7 令λ+μ=m,由等和线可知当EF∥BD且与圆C相切时m取最大值. 作AN⊥EF,垂足为点N,交BD于点M. 因EF∥BD,故△AMB∽△ANF. 由等和线可知此时λ+μ=3. 所以λ+μ最大值为3. 17世纪初,笛卡尔建立了他的坐标系,这是变量数学的先导和基础,深刻地影响了数学的发展道路.我们现在看来十分简单的笛卡尔坐标系,经过仿射变换成为仿射坐标系,借助平面向量基本定理的推导让我们进一步地理解直线截距式方程就是等和线的概念.向量是连接几何与代数的有效手段,通过建系使点坐标化,进而几何的目标可以通过代数达到,而代数的语言也可以用几何解释.
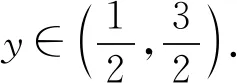
2 等和线求面积
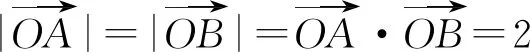
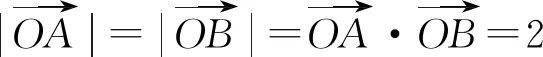


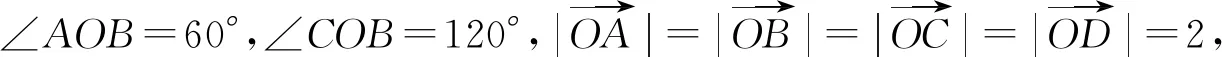
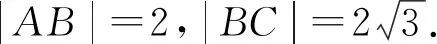
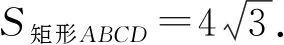
3 等和线求最值