过椭圆上任意一点作椭圆切线的两种尺规方法

北京市第五中学通州校区(101101)田朋朋

研究椭圆切线尺规作图方法的文章有很多,文[1]中介绍了勒姆柯尔、舒马赫、高斯三位数学家从椭圆外一点作椭圆切线的三种极点极线作法,精妙至极,令人叹为观止.研究从椭圆上一点作椭圆切线的文章也有很多,但大多数作法步骤繁多,且需要给定椭圆的中心、焦点、对称轴、顶点、准线等,依赖性较强.文[2]中在分别给定椭圆的焦点、顶点、对称轴的情况下给出了三种相对简洁的椭圆切线作法,其中方法一用到了椭圆的光学性质作图.文[3]中首先通过作图找到了椭圆的中心,然后在作出椭圆中心弦的基础上,给出了过椭圆上一点作切线的尺规方法.本文根据高等几何中极点极线的性质与对偶原则,给出了只用一把直尺从“中心、对称轴、焦点、顶点、准线”等一概不知的椭圆上任意一点作椭圆切线的两种尺规作法.

定义1[4]给定二次曲线C,如果两点P,Q(P,Q不在曲线C上)连线与二次曲线交于两点M1,M2,且(M1M2,PQ)=-1,则称P,Q关于二次曲线C调和共轭,或称点Q与点P关于二次曲线C互为调和共轭点.

对于二次曲线外的一个定点,它关于这个二次曲线调和共轭点的轨迹是一条直线,这条直线叫做该定点关于此二阶曲线的极线,该定点叫做这条直线关于此二次曲线的极点.

如图1,P为不在二次曲线上的点,过点P作二次曲线的两条割线依次交二次曲线于点E,F,G,H,连接EH,FG交于点N,连接EG,FH交于点M,则直线MN为点P关于此二次曲线的极线,点P称为直线MN关于此二次曲线的极点;同时也有直线MP为点N关于此二次曲线的极线,点N称为直线MP关于此二次曲线的极点.

图1

性质1[1]若点P在二次曲线上,则点P关于此二次曲线的极线为过点P二次曲线的切线;若点P在二次曲线内,则点P关于此二次曲线的极线为与以点P为中点的弦平行的直线;若点P在二次曲线外,则点P关于此二次曲线的极线为过点P作二次曲线的两条切线的切点连线(如图2).

图2

性质2[1]如果P点的极线通过Q点,则Q点的极线也通过P点.

证明设点P(x0,y0),以椭圆为例,则点P对应的极线方程为若设Q点坐标为(x1,y1),则有成立.又因点Q对应的极线方程为所以此直线通过点P(x0,y0).证毕.

其实,性质2 为配极变换中的基本性质,是一种特殊的对偶原则.因椭圆也属于二次曲线,下面利用上述定义和性质给出过椭圆上任意一点作椭圆切线的两种新方法.

方法1(1)如图3,椭圆上有一点P,任取一斜向割线PQ,并在异于PQ的地方取割线AB,AC,设PQ和AB交于点E,PQ和AC交于点F;

图3

(2)如图4,连结直线BP和直线QA交于点S,连结直线AP和直线QB交于点T,连结直线PA和直线CQ交于点M,连结直线AQ和直线PC交于点N,连结直线ST和直线MN交于点O,连结直线OP和直线OQ,则OP和OQ为椭圆的两条切线.

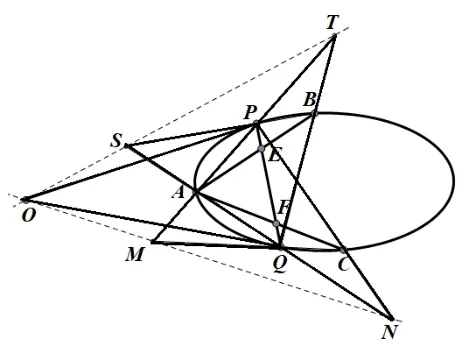
图4

证明根据定义1,点E关于椭圆的极线为直线ST,点F关于椭圆的极线为直线MN; 连结直线ST和直线MN交于点O,则点E关于椭圆的极线为ST且经过点O,根据

性质2,点O关于椭圆的极线也经过点E; 同理,点F关于椭圆的极线为MN且经过点O,点O关于椭圆的极线也经过点F;综上所述,点O关于椭圆的极线经过直线EF.又因为直线EF交椭圆于P,Q两点,根据性质1,即可得到OP和OQ为椭圆的两条切线.

方法2(1)作法与方法1 中的(1)相同.

(2)如图5,连结直线BP和直线QA交于点S,连结直线AQ和直线PC交于点N; 连结直线NF和直线SE交于点O,连结直线OP,则OP为椭圆的切线.

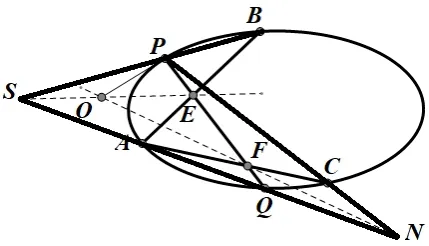
图5

证明补全图5 中的部分直线得到图6,根据定义1,点M关于椭圆的极线为NF且经过点O,根据性质2,点O关于椭圆的极线也经过点M; 同理,点T关于椭圆的极线为SE且经过点O,点O关于椭圆的极线也经过点T;综上有点O关于椭圆的极线经过直线MT.又因为直线MT交椭圆于P,A两点,根据性质1,即可得到OP为椭圆的切线.

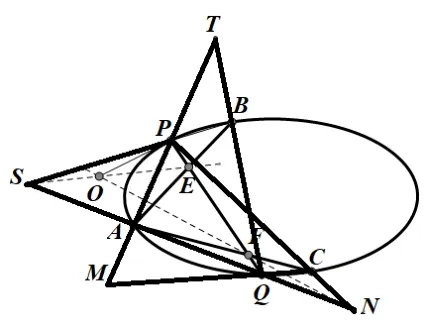
图6