关于二次曲线切线的研讨
2012-11-15黄振华
黄振华
(湖北师范学院 数学与统计学院, 湖北 黄石 435002)
1 记号
为了方便起见,本文引进下面的一些常用记号[1]:
F(x,y)≡a11x2+2a12xy+a22y2+2a13x+2a23y+a33
F1(x,y)≡a11x+a12y+a13
F2(x,y)≡a12x+a22y+a23
F3(x,y)≡a13x+a23y+a33
Φ(x,y)≡a11x2+2a12xy+a22y2
二次曲线的方程为
F(x,y)≡a11x2+2a12xy+a22y2+2a13x+2a23y+a33=0
(1)
过M0(x0,y0) 点,且具方向X,Y的直线方程为
(2)
将直线(2) 代入二次曲线(1) 得方程:
Φ(X,Y)·t2+2[F1(x0,y0)·X+F2(x0,y0)·Y]t+F(x0,y0)=0
(3)
2 概念
定义1[1]如果直线与二次曲线相交于相互重合的两个点,那么这条直线就叫做二次曲线的切线,这个重合的交点叫做切点;如果直线全部在二次曲线上,我们也称它为二次曲线的切线,直线上的每一个点都可以看成是切点.
定义2[1]二次曲线(1) 上满足条件F1(x0,y0)=F2(x0,y0)=0的点M0(x0,y0)叫做二次曲线的奇异点.即:二次曲线的奇异点就是二次曲线的中心在二次曲线上的点.二次曲线的非奇异点叫做二次曲线的正常点.

引理 二次曲线上若有奇异点,则此二次曲线必为退化二次曲线.
证明 对于奇异点M0(x0,y0) ,有
F(x0,y0) =F1(x0,y0)=F2(x0,y0)=0
因为
F(x0,y0)=x0F1(x0,y0)+y0F2(x0,y0)+F3(x0,y0)=0
所以有
F3(x0,y0)=0,
从而线性方程组

有解(x0,y0) .即齐次线性方程组
有非零解(x0,y0,1),所以I3=0.故二次曲线为退化二次曲线.
由定义及直线与二次曲线的相关位置的讨论,二次曲线的切线是以下两种情形:
情形1.Φ(X,Y)≠0 时,(3) 是关于t的一元二次方程,当
△=[F1(x0,y0)·X+F2(x0,y0)·Y]2-Φ(X,Y)·F(x0,y0)=0
时,直线(2) 与二次曲线(1) 相切;
情形2.Φ(X,Y)=0 时,F1(x0,y0)·X+F2(x0,y0)·Y=0,且F(x0,y0)=0 时,(3) 是恒等式,任何t值(实的或虚的)都满足,直线(2) 全部在二次曲线(1) 上,成为二次曲线的组成部分,直线 (2)与二次曲线(1) 也相切.
3 二次曲线过一定点的切线
下面就点M0(x0,y0)及二次曲线(1)的特征对二次曲线的切线进行研讨.
3.1 点M0(x0,y0)在二次曲线上
3.1.1 若M0(x0,y0) 为二次曲线(1) 的正常点,即F(x0,y0)=0,F1(x0,y0) 与F2(x0,y0) 不全为零时,由直线(2) 与二次曲线(1) 相切的条件F1(x0,y0)·X+F2(x0,y0)·Y=0 得:
X:Y=-F2(x0,y0):F1(x0,y0)
所以过M0(x0,y0) 点的切线方程为
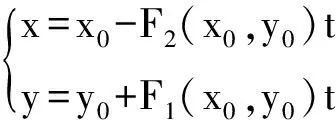
3.1.2 若M0(x0,y0) 为二次曲线(1) 的奇异点,即F(x0,y0)=F1(x0,y0)=F2(x0,y0)=0,此时,任何直线的方向X:Y都满足相切的条件F1(x0,y0)·X+F2(x0,y0)·Y=0,通过M0(x0,y0)点的任意直线都是二次曲线(1) 的切线.
定理1[1]如果M0(x0,y0)是二次曲线(1) 的正常点,那么通过M0(x0,y0)的切线方程是

是切点;如果M0(x0,y0)是二次曲线 (1)的奇异点,那么通过M0(x0,y0)点的每一条直线都是二次曲线(1)的切线.
3.2 点M0(x0,y0)不在二次曲线上
3.2.1 二次曲线(1)为非退化二次曲线时,二次曲线上没有奇异点.因为M0(x0,y0)点不在二次曲线上,所以过M0(x0,y0)的切线也不在二次曲线上,故切线是上述情形1,由
[F1(x0,y0)·X+F2(x0,y0)·Y]2-Φ(X,Y)·F(x0,y0)=0
及Φ(X,Y)≠0所确定的X:Y为方向的直线:

即为二次曲线 (1)过M0(x0,y0)的切线.
或者,因为此时二次曲线上没有奇异点,可设二次曲线上的正常点M1(x1,y1)为切点,则切线方程为[1]:
a11x1x+a12(x1y+y1x)+a22y1y+a13(x+x1)+a23(y+y1)+a33=0
(4)
又M0(x0,y0)点在切线上,所以
a11x1x0+a12(x1y0+y1x0)+a22y1y0+a13(x0+x1)+a23(y0+y1)+a33=0
且
由以上两方程确定的M1(x1,y1)代入 (4)式便得所求的切线方程.
例1 求二次曲线x2-xy+y2-1=0 通过点(0,2) 的切线方程.
解法一 ∵F(0,2)=3≠0,∴(0,2) 不在二次曲线上,设过(0,2) 的直线为
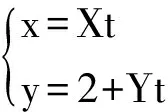

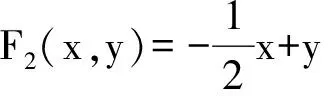
由相切条件
△=[F1(x0,y0)·X+F2(x0,y0)·Y]2-Φ(X,Y)·F(x0,y0)=0
得:(-X+2Y)2-3(X2-XY+Y2)=0, 即2X2+XY-Y2=0,显然满足Φ(X,Y)≠0,所以X∶Y=-1∶1,或X∶Y=1∶2.故所求切线是x-(y-2)(-1)=0,即x+y-2=0或2x-(y-2)=0,即2x-y+2=0.
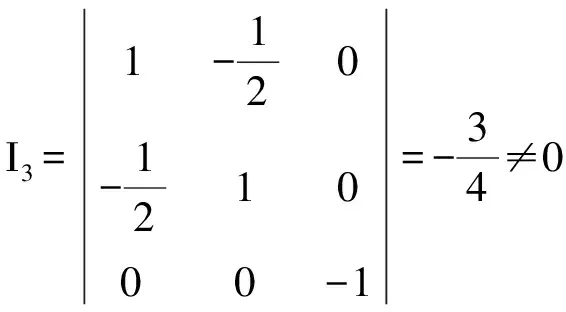
∴此曲线属非退化的,设二次曲线上的正常点
M1(x1,y1) 为切点,则切线方程为:
(5)
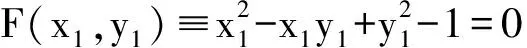
3.2.2 二次曲线 (1)为退化二次曲线时,退化的中心二次曲线有唯一奇异点(即中心);退化的线心二次曲线若有奇异点则有无穷多奇异点(它们在一条直线上),即中心直线上的点都是奇异点.根据定理1和二次曲线的切线定义,过二次曲线外一点M0(x0,y0)的切线就是二次曲线上的奇异点与M0(x0,y0)点 的连线.所以,退化中心二次曲线有唯一一条切线,而有奇异点的退化线心二次曲线有无数条切线.没有奇异点的退化二次曲线,过二次曲线外一点M0(x0,y0) 的切线不存在.
定理2 有奇异点的退化二次曲线,通过曲线外一点的切线,就是这点与二次曲线上的奇异点的连线;没有奇异点的退化二次曲线,通过曲线外一点的切线不存在.
4 二次曲线平行于一定方向的切线
下面就方向X:Y及二次曲线(1) 的特征对二次曲线的切线进行研讨.
4.1 对于非退化二次曲线
因非退化二次曲线上没有奇异点,设二次曲线上一正常点M0(x0,y0) 为切点,则切线方程为
a11x0x+a12(x0y+y0x)+a22y0y+a13(x+x0)+a23(y+y0)+a33=0
即xF1(x0,y0)+yF2(x0,y0)+F3(x0,y0)=0.
其方向为-F2(x0,y0):F1(x0,y0) .
设切线平行于一定方向X∶Y,则 -F2(x0,y0):F1(x0,y0)=X∶Y,即得切线平行于一定方向X∶Y的条件为XF1(x0,y0)+YF2(x0,y0)=0 .
另一方面F(x0,y0)=0由此两方程可确定切点M0(x0,y0)从而得平行于一定方向X∶Y的切线方程为:
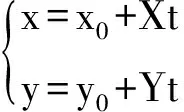
例2 求曲线x2+4xy+3y2-5x-6y+3=0 平行于直线x+4y=0的切线方程.
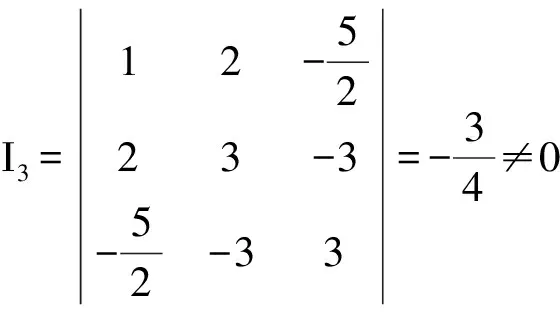
此曲线属非退化的,设二次曲线上一正常点M0(x0,y0)为切点
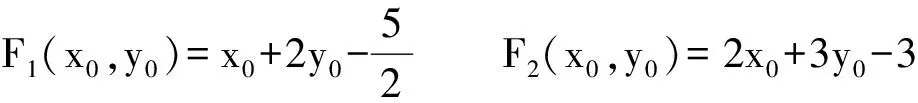
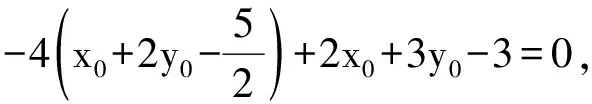

4.2 对于退化二次曲线
因退化二次曲线是由两直线(实的或虚的)组成,且两直线的方向都是渐近方向,根据二次曲线切线的两种情形,有:
4.2.1 定方向X∶Y为非渐近方向时,若二次曲线(1) 存在奇异点M0(x0,y0),则平行于一定方向X∶Y的切线方程为:

若二次曲线(1) 不存在奇异点,则平行于一定方向X∶Y的切线不存在,或也可以用4.1的方法解决.
4.2.2 定方向X∶Y是渐近方向时,则切线是组成二次曲线的直线.
例3 求退化二次曲线(x-y+1)(x-y-1)=0 平行于:
1) 非渐近方向X∶Y=1∶2 的切线方程;
2) 渐近方向X∶Y=1∶1的切线方程.
解 此退化二次曲线即
x2-2xy+y2-1=0
∴F1(x,y)=x-y,F2(x,y)=-x+y
且不存在奇异点,所以:
1) 平行于非渐近方向X∶Y=1∶2的切线不存在,或者设二次曲线上一正常点M0(x0,y0)为切点,由平行条件
x0-y0+2(-x0+y0)=0
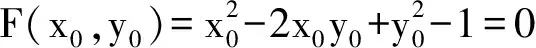
联立两方程,无解.所以切线不存在.
2) 平行于渐近方向X∶Y=1∶1的切线就是组成二次曲线的两直线x-y+1=0和x-y-1=0.或也可以用4.1的方法求得.
参考文献:
[1]吕林根,许子道.解析几何[M].北京:高等教育出版社,2006.
[2]吕林根.解析几何学习辅导书[M].北京:高等教育出版社,2006.
[3]刘耀武.关于二次曲线的切线及奇异点的探讨[J].高等数学研究,2010,13(2):14~16.
[4]刘德金.关于二次曲线切线问题的两点注记[J].高等数学研究,2012,15(2):5~7.
