几何条件代数化轨迹视角寻新解——对2022年新高考Ⅱ卷第21题的探究及溯源

深圳市龙华区教育科学研究院附属外国语学校(518109)钟文体

1.试题呈现及分析

例1(2022年新高考Ⅱ卷第21 题)设双曲线C:的右焦点为F(2,0),渐近线方程为y=±3x.

(1)求C的方程;

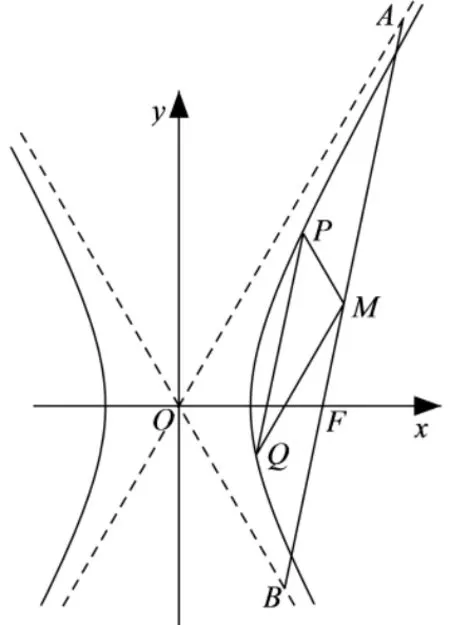
(2)过F的直线与C的两条渐近线分别交于A,B两点,点P(x1,y1),Q(x2,y2)在C上,且x1>x2>0,y1>0.过P且斜率为的直线与过Q且斜率为的直线交于点M,请从下面①②③中选取两个作为条件,证明另外一个条件成立:①M在AB上; ②PQ//AB; ③|MA|=|MB|.

注若选择不同的组合分别解答,则按第一个解答计分.

试题分析本题以直线和双曲线为载体,具体考察双曲线的方程与渐近线、直线的方程、韦达定理、两点间距离公式等解析几何的必备知识,涉及数形结合思想、转化与化归思想,着力考察数学抽象、逻辑推理、直观想象、数学运算等数学学科核心素养.第(1)问是常规的基础题,难度不大,只要学生熟悉双曲线的相关要素(实轴、虚轴、焦点、渐近线等)以及它们之间的关系即可正确解答.第(2)问是典型的结构不良问题[1],初始条件和目标结论都不明确,需要学生根据自身的知识经验,选择最有把握的组合进行解答,有效考察学生思维的灵活性和深刻性.解答时需要将所给的三个几何条件等价转化为代数条件(解析化),渗透了数形结合等平面解析几何中的核心数学思想,具有一定的区分度,体现了高考的选拔功能.

解答分析(1).(过程略)

(2)由条件x1> x2>0 可知直线PQ的斜率存在,下面再分析直线AB的斜率是否存在.若选择①②或②③作为条件,则由PQ//AB可知直线AB的斜率存在.若选择①③作为条件,则M为线段AB的中点,假设直线AB的斜率不存在,则由双曲线的对称性可知M在x轴上,即为焦点F,此时由双曲线的对称性可知P、Q关于x轴对称,从而x1=x2,与已知条件矛盾,所以直线AB的斜率存在.因此,不管如何选取条件,直线AB的都斜率存在.

评注一般情况下,在设直线方程时,为了保证解答的严谨性,需要分直线的斜率存在与不存在两种情形进行讨论,但斜率不存在的情形通常较容易解决,且不是问题的本质.本题所给的条件x1> x2>0 隐含了直线AB的斜率存在,避免了繁琐的分类讨论,减轻了学生的答题负担,体现了高考的人文关怀.

思考由条件可知点M由点P和点Q确定,当点P和点Q变动时,点M也随之变动.因此,自然的思路是设出直线PM和直线QM的方程,再联立求出点M的坐标.但可以预想到,此时M的坐标的表达式会比较复杂,若学生不具备敏锐的观察力和较高的数学运算能力,将给后面的计算带来极大的困难.另一方面,所给的三个条件都不涉及直线PM和QM,但有两个条件( ①和③)涉及点M.因此,以M为主体,先设出点M的坐标,是更优的解题途径.

设直线AB的斜率为k,点M的坐标为(x0,y0),则直线AB的方程为y=k(x-2).

条件①的代数化:易知,M在AB上⇔y0=k(x0-2).

条件②的代数化:由题设知直线PM的斜率为直线QM的斜率为故直线PM和QM的方程分别为y - y0=和y - y0=将点P和点Q的坐标分别代入,得y1-两式相减得因此,直线PQ的斜率.

移项整理得

即

也即x0-xN+k(y0-yN)=0,因此x0+ky0=xN+kyN,将xN和yN代入得.所以|AM|=.

综上,①⇔y0=k(x0-2); ②⇔3x0=ky0; ③,成功将三个几何条件转化为代数条件,即关于x0,y0,k的代数表达式.进一步注意到三个代数表达式都是关于x0和y0二元一次方程,任选两个都可以很方便地求出x0和y0,再代入剩下的表达式进行计算即可.事实上,任选两个条件计算x0和y0的结果都是一样的,即.

评注解析几何问题的解答应遵循“多想少算”的原则,恰当地设点和直线可以有效减少计算量.上面的解答以点M为主体,巧妙地设点M的坐标,使得整个解题过程顺利推进.

2.试题溯源

高考试题具有“源于教材,高于教材”的特点,例1 能否从教材中找到源头呢? 在将条件③进行代数化时,曾得到.于是,当直线AB的斜率为定值k时,线段AB的中点在一条直线上.笔者查阅教材发现,人教A 版《普通高中课程标准实验教科书·数学》(“旧教材”)选修2-1 第49 页第8 题有类似的题目:

例2已知椭圆,一组平行直线的斜率是.

(1)这组直线何时与椭圆相交?

(2)当它们与椭圆相交时,证明这些直线被椭圆截得的线段的中点在一条直线上.

人教A 版《普通高中教科书·数学》(“新教材”)选择性必修第一册第116 页第14 题也有同样的题目.事实上,在一般的圆锥曲线中,也有类似例2 的结论.

结论1椭圆平行弦的中点在一条过椭圆中心的直线上.

证明不妨设椭圆方程为当弦平行于x轴或平行于y轴时,结论显然成立.下面考虑斜率存在且不为零的情形,设弦所在直线的方程为y=kx+m(k0),与椭圆方程联立,消去y,得(k2a2+b2)x2+ 2ka2mx+a2(m2-b2)=0,设弦中点坐标为(x0,y0),与椭圆的交点坐标分别为(x1,y1)、(x2,y2),由韦达定理可知.因此,从而弦的中点在直线上.

结论2双曲线平行弦的中点在一条过双曲线中心的直线上.

结论3抛物线平行弦的中点在一条平行于抛物线对称轴的直线上.

证明不妨设抛物线方程为y2=2px(p>0),当弦平行于y轴时,结论显然成立.下面考虑斜率存在的情形,设弦所在直线的方程为y=kx+m(k0),与抛物线方程联立,消去y,得k2x2+2(km-p)x+m2=0,设弦中点坐标为(x0,y0),与抛物线的交点坐标分别为(x1,y1)、(x2,y2),由韦达定理可知从而弦的中点在直线上.

上述三个结论具有深刻的高等数学背景,在大学的解析几何课程中,圆锥曲线平行弦中点的轨迹称为平行弦的共轭直径.椭圆的平行弦的斜率与其共轭直径的斜率之积为常数;双曲线的平行弦的斜率与其共轭直径的斜率之积为常数;抛物线任意平行弦的共轭直径均平行于抛物线的对称轴.

下面从轨迹的视角重新审视例1.

根据结论2,当例1 中的直线AB的斜率为定值k时,线段AB的中点N在直线上.设例1 中M的坐标为(x0,y0),直线PQ的斜率为t,在将条件②进行代数化时曾得到关系式,即因此,当直线PQ的斜率为定值t时,点M在直线上.另一方面,在将条件③进行代数化时曾得到线段AB中点N(xN,yN)的坐标为.

若选择①②,则t=k,即点M在直线上.联立解得M的坐标为因此,点M和点N重合,即点M为线段AB的中点,所以|MA|=|MB|.

若选择①③,则点M为线段AB中点,故M的坐标为由于点M在直线上,故解得t=k,所以PQ//AB.

若选择②③,则点M(x0,y0)在线段AB的垂直平分线上,与直线联立,解得x0=,将点N的坐标代入,得,同理y0=yN,故点M和点N重合,所以M在AB上.

评注上述解答将原问题转化为关于两条直线的位置关系以及点与直线的位置关系,解答过程充分利用了点M在直线上这一结论.事实上,一般的双曲线中也有类似的结论,有兴趣的读者可以作进一步的探究.

结语圆锥曲线是高考的必考内容,考察的形式多样,通常都有一道解答题作为压轴题,运算量和思维量较大,学生需要有较好的思维品质才能正确完整地解答.本文探究的高考真题改编自教材习题.事实上,近年来的高考数学试题中涌现了一批源自教材的优秀试题.可见,在日常的教学和复习备考中,应引导学生深入研究教材中的例习题.教材包含最基本的数学知识,是学生获得系统知识的主要材料,也是高考命题的鲜活源泉.罗增儒教授曾指出:“教材是课程的载体,所以高考命题最具体、最方便的依据其实就是教材”.引导学生钻研教材中的例习题,深挖其深刻的背景,体会其丰富的数学思想,真正将书本的知识内化为学生自己的知识.