2022年全国高考数学“函数与导数”试题研究

佛山市禅城区教育发展中心教学研究室(528000)曾庚平

1 问题提出

函数是现代数学最基本的概念,是描述客观世界中变量关系和变化规律的数学语言和工具,在解决实际问题中发挥着重要作用.现行的数学课程标准将函数作为四条主线之一,并贯穿必修和选择性必修课程,其中在必修部分教授函数的概念与性质、基本初等函数、函数的应用,在选择性必修部分教授数列、一元函数的导数及其应用(本文不研究数列试题)[1].在历年高考题中,函数与导数都是重要的考查内容,以函数与导数试题来考查学生数学抽象、数学建模、数学运算、直观想象和逻辑推理核心素养.

本文以2022年4 份(新高考Ⅰ卷,新高考Ⅱ卷,全国甲卷理科,全国乙卷理科)全国高考数学卷中的函数与导数试题为例(不研究数列试题),从课标中体现数学学科核心素养的两个方面——情境与问题、知识与技能[1]进行分析,探讨其中考查的核心素养和数学思想.本文拟讨论的问题如下:(1)试题中考查的情境与问题、知识与技能有什么特点?(2)试题主要考查哪种数学素养?(3)试题蕴含哪些数学思想?

2 选填题分析

2.1 整体分析

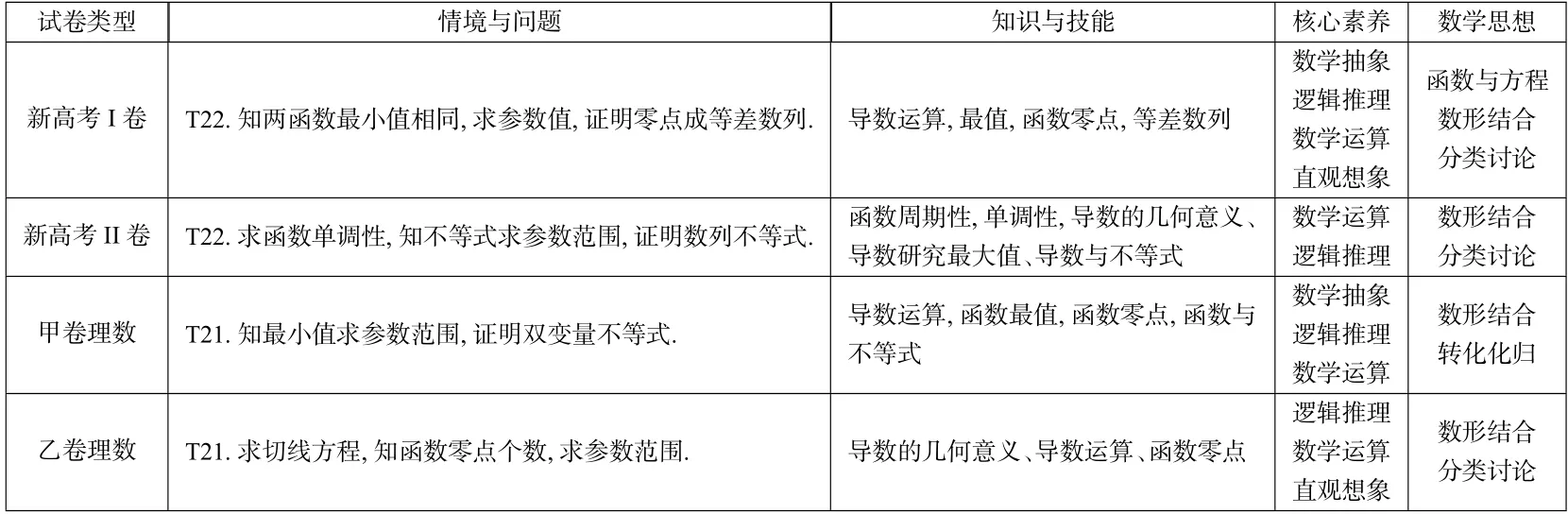
从情境与问题、知识与技能、核心素养与数学思想四个方面对函数与导数选择填空题进行分析,结果如表1所示.

表1 2022年4 份试卷中函数与导数选填题考查分析表

由表1 可知,新高考Ⅰ卷函数与导数考查的力度最大,直接考查的试题有5 题,与立体几何结合的有1 题,合计6 题,甲卷理数其次,考查4 道题,其余两套卷均考查3 道题.所有试题均为数学情境,但是问题的呈现形式非常丰富,既有具体函数图象与性质的研究,也有抽象函数性质的探索,还有通过对数量关系和图形关系的分析,构造函数模型,通过研究函数性质,解决相关问题.对三角函数的考查既关注三角函数的周期性、对称性、单调性、最值、零点等传统知识,也尝试从三角函数的切线,重要的三角函数不等式等新的视角.由于函数与导数包含的知识点众多,所以多数试题都是多个知识点联系在一起进行考查,体现综合性,如新高考Ⅰ卷第15 题在考查函数切线的同时考查导数研究函数单调性、最值等.函数导数试题还突出体现创新性和选拔性的要求.

函数导数突出的是模型思想,通过对现实问题和数学问题数量和数量关系的观察、归纳、概括,抽象出函数模型,再通过逻辑推理和数学运算研究函数,从而解决实际问题或数学问题.比如题目中涉及的比较数的大小问题,要求学生能够从具体表达式中抽象出一般规律和结构,构造相应的函数模型,从而解决问题.

2.2 例题分析

选取2 道选择题进行深入分析.

例1(2022年新高考Ⅱ卷第8 题)若函数f(x)的定义域为R,且f(x+y)+f(x-y)=f(x)f(y),f(1)=1,则=( )

A.-3B.-2C.0D.1

本题以抽象函数为载体,考查对函数概念的理解,函数性质的研究,主要考查逻辑推理和数学抽象素养.对函数概念的理解不是记住函数定义域的言语表达,而是要抓住函数概念的本质,把握三要素的关系,理解函数符合的含义.对函数性质要抓住性质的本质,既能从图象直观判断性质,又能根据解析式研究性质,还要能基于函数满足的等量关系研究抽象函数性质.本题要求考生充分理解f(x+y)+f(x-y)=f(x)f(y),通过恰当赋值,推断出函数f(x)的奇偶性和周期性,将求和问题转化为求一个周期内的六个函数值f(1),f(2),···,f(6),解题思路如图1所示:

图1

例2(2022年新高考Ⅰ卷第7 题)设a=0.1e0.1,b=,c=-ln 0.9,则( )

A.a

本题给定三个无法直接计算数值的表达式,需要考生认真分析其中隐含的特征和规律,抽象函数模型,用导数研究函数的单调性,实现对数值大小的比较,考查数学抽象、逻辑推理、数学运算等核心素养,体现综合性和创新性.

本题要求学生能够透过现象,发现本质,将三个看似毫无关联的表达式联系起来.实际上,a=0.1e0.1,,所以这些表达式都与0.1 有关,可以看成某个函数在0.1 处的函数值,因此,我们可以构造恰当函数,转化为研究函数单调性,来解决问题.当然构造的函数不同会导致研究过程的复杂程度差异巨大,这又进一步考查学生思维的灵活性和批判性.比如对于a,b的比较,构造函数有以下选择:f3(x)=(1-x)ex -1,0< x <1,此外,由lna-lnb=0.1 + ln 0.1 + ln 9=-(-0.1)+ ln(1-0.1),还可以构造f4(x)=ln(1+x)-x,-1< x <0.不难发现,研究f4(x)是最简单的,其本质就是切线不等式lnx≤x-1,由此不但能判断a < b,由还可判断出b > c.由a-c=0.1e0.1+ln(1-0.1),再构造函数g(x)=xex+ln(1-x)(0

从上述两道题目看,与往年试题相比,2022年函数与导数选填题更加重视对数学抽象和逻辑推理学科素养的考查,加强对思维品质的考查,强调独立思考能力和创新意识.

3 解答题分析

3.1 整体分析

对四份试卷中函数与导数解答题的考查情况进行分析,结果如表2所示.

表2 2022年4 份试卷中函数与导数解答题考查分析表

由表2 可知,每份试卷的函数导数解答题都处于压轴题的位置,四道题的函数载体均为含lnx,ex的函数,且都带有参数,情境载体常规不复杂,设问方式上则独具匠心,构思巧妙,在传承中创新,于平淡中见奇.新高考Ⅰ卷考查常见函数f(x)=ex -x,g(x)=x-lnx,它们满足性质f(lnx)=g(x)(x>0),g(ex)=f(x),命题者抓住这种“对偶”性质,探究f(x)-b,g(x)-b零点的个数与数量关系,设问巧妙地与数列知识结合.新高考Ⅱ卷考查恒成立问题确定参数范围,同时为第(3)问数列型不等式的证明提供放缩的方向.甲卷理数要证明的是一个函数的两个零点满足的双变量不等式,这类问题最早可以追溯到2010年高考天津卷理科第21 题,在2016年课标Ⅰ卷理科第21 题,2021年新高考Ⅰ卷理科第22 题都曾考查过,这些题目都证明两根之和的不等式,但是本题要证明的是两个零点乘积的不等式,并且函数形式有所创新,所以提出的问题跨度更大,挑战性更高,需要学生深入思考和探究.

函数不仅仅是高中阶段重要的数学内容,也是大学数学及其它相关学科的基础,是初等数学和高等数学联系的桥梁.所以高考数学重视通过导数试题考查学生的创新能力,以达到区分和选拔的目的[2].四道题着重考查运用导数工具研究函数性质的能力,鼓励学生打破常规、多角度、创造性地解决问题,突出考查数形结合、分类讨论、函数与方程等思想.

3.2 例题分析

下面选取2 道解答题进行深入分析.

例3(2022年新高考Ⅰ卷第22 题)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.

(1)求a;

(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.

本题以两个简单含参函数为载体考查学生直观想象、逻辑推理素养,考查数形结合、函数与方程、转化化归等思想,体现综合性和创新性的要求.本题体现了高考命题中“低起点、多层次、高落差、重本质”的特点,大多数考生都容易入手,求得两个函数的最小值,并聚焦到解方程接着,对理性思维的考查逐步提高,要在函数与方程思想的引领下,转化为研究函数第(2)问突出体现研究函数的一般方法,即先研究部分性质(主要是单调性),画出两个函数的大致图象,获得问题解决的思路,然后再进行严密的代数推理,整个问题强调图形直观与代数推理的融合,解题思路如图2所示.

图2

例4(2022年高考全国甲卷理科第21 题)已知函数．

(1)若f(x)≥0,求a的取值范围;

(2)证明:若f(x)有两个零点x1,x2,则x1x2<1．

x >1 形式复杂,证明的难度较大.如果能关注到ex-lnx,将f(x)看成y=et+t-a与t=x-lnx的复合函数,那么结合y=et+t-a的单调性,已知条件化简为x1-lnx1=x2-lnx2.所以,原题转化为已知h(x)=x-lnx,且h(x1)=h(x2),x1x2,证明x1x2<1,从而大大简化解答过程.转化的关键是应用同构的思想,即根据式子的特征,将结构不同的代数式化为结构相同的代数式,发现本质,简化解答.同构变形的基础是两个重要的恒等式a=elna(a>0)和a=ln ea,以及常见函数模型,如本题中涉及的y=ex+x和y=x-lnx.

4 教学启示

高考评价体系下高考数学考查内容和命题方式在不断变化,强调对学科素养和关键能力的考查,2022年高考函数与导数试题都是设置数学情境,给出载体熟悉且简洁,提问方式多样且新颖,试题对理性思维和数学探究的考查更加深入,更加强调知识的融会贯通,更加体现创新性和选拔性的要求.基于上述分析,得出以下几点教学启示.

4.1 立足基本概念的理解

数学概念是构成数学大厦的基础,是形成数学知识体系的基本要素,是进行数学思维的细胞.在函数与导数这一板块,有很多重要的数学概念:函数的概念(定义域、值域、对应法则、表示方法)、函数的性质(奇偶性、单调性、最值、对称性、周期性)、函数零点、导数、极值点、不等式恒成立、不等式能成立,这些概念都比较抽象,符号化表征.在复习备考中首先要让学生深刻理解重要概念,把握概念内涵,理解概念的多元表征,建立概念之间的联系,才能更好地分析问题和解决问题.如:

函数的零点的学习要点:深刻领悟零点的概念、零点存在性定理以及函数零点与方程的根的等价转化关系,让学生在解决问题中能灵活转化,化繁为简.

函数的导数的学习要点:导数就是瞬时变化率,是切线的斜率;导数的正负可以判断原函数的单调性,进而研究极值、最值、画出函数图象的示意图等;导数绝对值的大小可以反映图象的变化快慢;导数本身也是一个函数,是函数图象的斜率关于自变量的函数.

函数的图象的学习要点:数形结合是函数与导数中蕴含的数学思想,一方面学生要能结合基本初等函数的图象和图象变换的相关知识画图,识图,根据图象判断函数性质,根据图象获得解决问题的直观思路;另一方面对于一些陌生函数,能先研究函数的定义域、奇偶性、单调性、特殊点和特征线等,根据上述性质画出函数草图,并进一步解决方程与不等式问题、恒成立与能成立问题等.

4.2 重视基本模型的研究

指数函数、对数函数、幂函数、三角函数是常见的基本初等函数,是刻画现实生活中某一类具体的变化的模型,由这些简单的函数适当组合、推陈出新,就可以构建令人耳目一新的函数形式,所以在复习中要引导学生研究常见的函数模型,比如通过对三次函数f(x)=ax3+bx2+cx+d(a0)的研究,体会导数在研究函数性质的强大作用.在此基础上,让学生进一步研究以下常见模型通过对这些函数的研究总结归纳导数研究函数的一般方法,体会函数载体在变而研究方法不变的思想.掌握常见函数模型的性质,在面对复杂函数的时候就能拨云见日,化繁为简,化生为熟,直击本质.

4.3 强调一般方法的引领

研究函数的一般方法强调几何直观与代数推理的融合,即面对一个函数时,先根据其解析式推断出部分性质,再根据性质画出函数的大致图象,结合图象获得问题解决的直观思路,最后再进行严密的代数推理,保证思维的严谨性,整个过程可以用图3 表示.

图3

导数是研究函数性质的利器,能定量刻画函数的变化,用导数可以研究函数的单调性、凹凸性、极值、最值、拐点等.导数内容博大精深,变化无穷,与导数相关的问题在呈现方式和设问方式必然不断创新.教学时要避免题型套路的直接灌输,避免囫囵吞枣式的机械套用,要强调导数概念本质的理解,抓住导数与单调性的关系这一核心,在一般方法的引领下,面对新颖或陌生的问题情境,让学生主动思考,积极探索,大胆尝试.

4.4 深化数学思想的渗透

数学思想是自然而平和的,它是揭示本源性问题的一个很平常、很自然的思考过程[3].转化化归、数形结合、函数与方程、分类讨论是解决函数与导数问题的重要数学思想.问题解决的过程就是一个不断转化和化归的过程:化陌生为熟悉、化繁杂为简单、化未知为已知.数形结合强调将“形”的直观与“数”的严谨相结合,即利用“形”的直观,“看”出思路,再发挥“数”的严谨,“写”出过程.函数与方程是分析实际问题数量关系、解决实际问题的两种重要模型,根据两者的关系,函数与方程可以相互转化.分类讨论是由于参数的影响,导致不能以统一的方式处理或者以同一种形式表达,从而需要根据参数不同的取值分情况研究.所以在教学中要注重数学思想方法的提炼,让学生能自觉应用数学思想分析问题和解决问题.