双圆弧谐波齿廓设计方法
2023-03-15杨玉虎周国成
杨玉虎,何 渠,解 然,周国成
(天津大学机械工程学院,天津 300350)
谐波齿轮传动具有大速比、结构紧凑、同时啮合齿数多及承载大等特点,在航空航天、仪表仪器及机器人领域中得到广泛应用.
20世纪 50年代,Musser[1]率先提出采用直线齿廓的谐波传动.但是,直线齿廓在啮合中会发生轮齿对称线偏转,因而存在啮合区间过小和尖点啮合的现象[2].Шyвaлoв[3]发现了直线齿廓的这种不足,并用图解法进行了验证,采用渐开线齿廓在一定程度能补偿直线齿廓的缺陷.沈允文等[4]采用使柔轮压力角稍大于刚轮压力角的方法,补偿柔轮变形对轮齿啮合性能的影响,发现柔轮压力角的修正量与传动比有关[5].León等[6]分析了模数、压力角和修正系数对齿廓啮合性能的影响,并辅以有限元仿真设计齿廓主要几何参数.
随着智能机器人与航空航天技术的快速发展,采用直线或渐开线齿廓已不能满足性能需求,人们开始探索新型齿廓.Гинэбypг[7]提出圆弧齿廓,这种宽齿槽齿形可有效改善齿根应力集中问题,柔轮轮齿柔性足以补偿啮合侧隙,且沿齿高方向的齿间楔形侧隙有利于形成润滑油膜.沈允文[8]通过理论和实验验证了采用圆弧齿廓谐波齿轮的可行性和合理性.曾世强等[9]比较了相同参数下渐开线和双圆弧齿廓的啮合性能,发现双圆弧齿廓的啮合区间大于渐开线齿廓.在此基础上,辛洪兵[10-11]研究了双圆弧齿廓参数的选取和设计方法,并总结一系列齿廓参数选取参考值.陈晓霞等[12-13]提出了双圆弧齿廓的弧长坐标表示方法,为双圆弧齿廓的解析表达及高效设计提出一种有效的方法.其后,Tang等[14]开展了双圆弧公切线齿廓的参数优化设计研究,分析了齿廓参数对齿廓共轭啮合区域及共轭齿廓差异的影响,并给出具体的单参数及多参数优化算例.但上述文献在齿廓设计中,总体上仍是依据经验给出柔轮齿廓参数,然后根据柔轮与刚轮齿廓的啮合性能迭代运算确定齿廓参数,设计效率低且缺少速比等工况参数的关联设计信息.
文献[14-16]从运动学分析出发,提出基于瞬心线的双圆弧齿廓设计方法,该方法避免了采用包络法必须反复进行的干涉检验,实现了齿廓特定点的精确共轭以及连续共轭啮合.注意到,日本学者 Ishikawa[17]提出根据柔轮齿顶点的运动轨迹进行二分之一映射和镜像的 S形齿廓设计方法.这种方法形象直观,齿廓能够实现连续啮合.但由于假定刚轮为齿条,因而在齿廓设计中忽略了柔轮齿歪斜和速比等运动信息,须进行复杂的齿廓修形[18].
本文针对现有圆弧齿廓依据经验和反复包络迭代计算确定齿廓设计参数的不足,提出根据柔轮齿顶相对刚轮的最大切向位移构造共轭齿廓的设计方法.从波发生器函数与速比等参数信息出发,通过分析柔轮齿顶的相对运动轨迹,提取柔轮齿顶的切向位移信息,据此构造柔轮的初始齿廓参数,进而完成共轭齿廓设计.
1 谐波齿轮传动概述
谐波齿轮的 3个主要零部件:刚轮、柔轮及波发生器,如图1所示.

图1 谐波齿轮传动主要部件Fig.1 Three main components of harmonic drive
波发生器与柔轮完成装配后,柔轮将按照波发生器形状产生相应的变形,啮合平面上分别产生径向变形 w、切向变形 u以及轮齿法线偏转 μ,柔轮齿位置发生相应变化,如图2所示.图中rm表示未变形柔轮中线的半径,红色箭头表示变形方向.
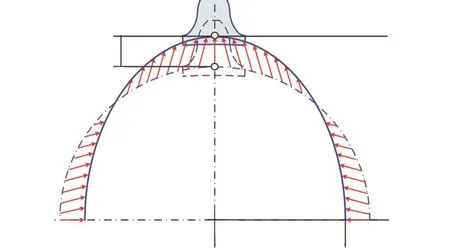
图2 柔轮变形中线Fig.2 Deformed neutral curve of flexspline
设柔轮变形曲线为标准椭圆,椭圆长短半轴分别为 a、b,长轴处最大径向变形量为 w0,变形曲线方程为
式中 e为椭圆偏心率,即
在波发生器的作用下,柔轮产生周期性弹性变形与刚轮形成周期性错齿运动,传动比为
式中:z1是柔轮齿数;z2是刚轮齿数;“-”表示波发生器与柔轮的转向相反.
2 柔轮双圆弧齿廓设计
2.1 齿廓参数
为建立柔轮齿廓的参数模型,以轮齿对称线为yf轴,对称线与中线交点为原点Of,建立与柔轮轮齿固连的局部坐标系 Ofxfyf,如图3所示.其中,r为变形前柔轮分度圆半径,ha、hf分别为齿顶高、齿根高.
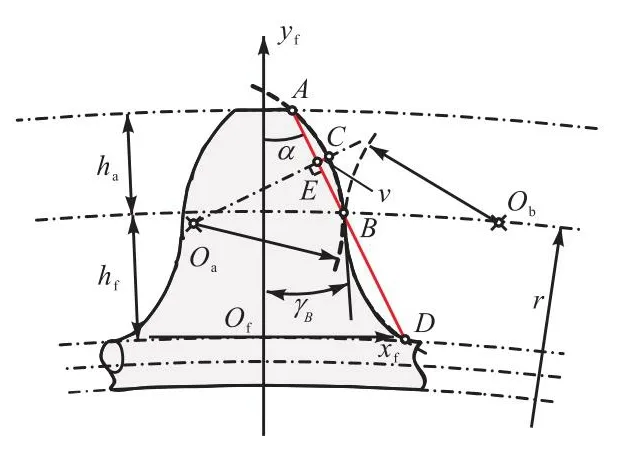
图3 柔轮齿廓参数Fig.3 Parameters of flexspline tooth profile
已知柔轮分度圆与齿厚比,则分度圆与齿廓曲线的交点B确定,过B点作与yf轴夹角为α的直线,称为齿廓基准线,α称为名义压力角[11].基准线分别交齿顶圆、齿根圆于A点、D点.
作 AB中垂线 EC,以 A、B、C 3点作齿顶圆弧,圆心为Oa.EC的长度v决定双圆弧齿廓的整体凹凸程度,将直接影响共轭齿廓的形状.以 B为公切点,过 B、D两点,作与圆弧 AB相切的圆弧 BD,作为齿根圆弧,圆心为Ob.公切点切线与yf轴夹角为γB.柔轮齿廓的基本设计参数如表1所示.
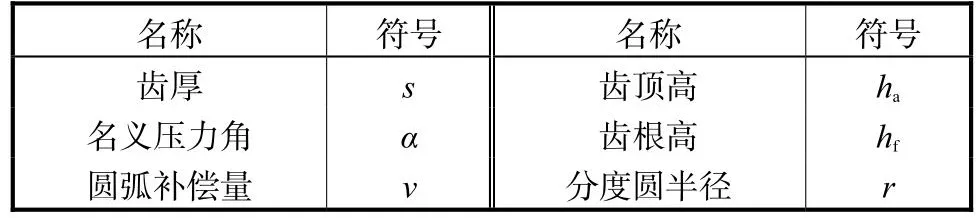
表1 柔轮齿廓参数定义Tab.1 Definition of tooth parameters for flexspline
2.2 齿廓方程
如图3所示,A、B、D 3点的位置矢量分别为
C位于AB的垂弦方向上,有
齿顶圆弧中心Oa和半径ρa由此确定,有
以B点为公切点,过齿根点D作齿根圆弧,圆弧中心Ob和半径ρb为
两段圆弧的公切点倾角为
采用弧长坐标表示齿廓方程[13],l为弧长参数,柔轮齿廓及其法线方程可表示为如下分段函数.
(1) AB齿顶圆弧段函数分别为
(2) BD齿根圆弧段函数分别为
3 轮齿运动学
3.1 啮合端各构件的相对运动关系
假定刚轮固定,波发生器为输入构件,柔轮为输出构件.以波发生器回转中心 O为原点,长轴为 y轴,建立刚轮坐标系 Ocxcyc,如图4所示.对应柔轮与刚轮齿的对称线与 y轴重合时为初始位置.图4中,Owxwyw是与波发生器固连的动坐标系,初始时刻与刚轮坐标系重合.
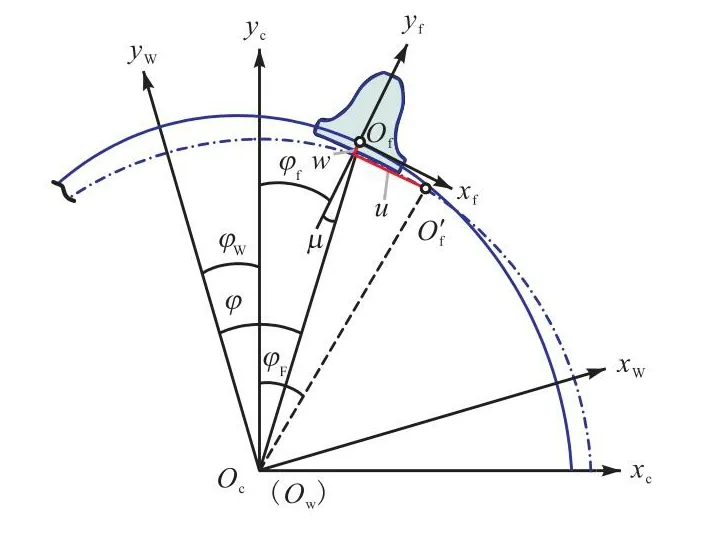
图4 各构件的相对运动关系Fig.4 Relative motion relationships among the three components
设波发生器由初始位置逆时针转动Wφ角,同时柔轮输出端相对初始位置顺时针转动Fφ角,关系为
波发生器相对柔轮啮合端的转角为 φ,啮合端坐标系原点由Of′点变形至 Of点.采用标准椭圆波发生器时,变形量函数为
Of点相对点的位移可用矢量表示
设柔轮齿上任一点 N在动坐标系 Ofxfyf下的位置矢量为,其在 Ocxcyc下的矢量可表示为
式中
根据式(20),对应柔轮齿啮入到啮出转角的范围,可得柔轮公切点B的运动轨迹方程有
相应的B点运动速度矢量可表示为
3.2 柔轮齿公切点运动轨迹分析
为进一步探讨轮齿的运动规律和变形情况,假定柔轮输出端固定,波发生器主动,刚轮从动.根据式(22)得到啮合端轮齿在一个周期内的运动轨迹Oi(1,2,…,n),如图5所示,其中O1对应完全啮合,On对应完全脱开;vm为柔轮齿的最大切向位移,是柔轮齿自身的偏转以及柔轮的切向变形共同导致.
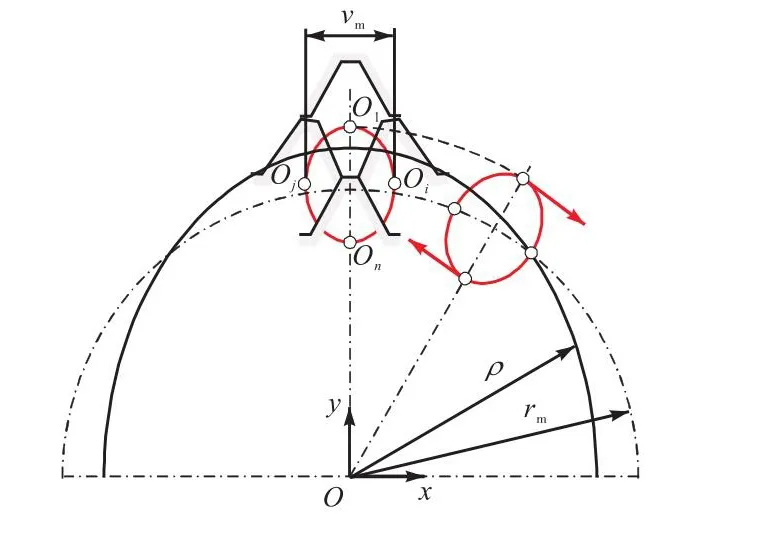
图5 柔轮输出端固定时柔轮齿的相对运动轨迹Fig.5 Trajectory of flexspline tooth when the output end is fixed
利用反转法,齿廓公切点 B的运动轨迹在柔轮输出端下可表示为
因此,最大切向位移为
vm用于设计齿顶圆弧的补偿量 EC,该补偿量决定了双圆弧齿廓的凹凸程度,对共轭啮合区间角度有重要影响.
3.3 柔轮齿顶圆弧的连续共轭条件
如图6所示,对比直线齿廓与双圆弧齿廓及其运动轨迹,前者的齿廓法向矢量为常值,运动过程中共轭解非常少;而后者齿廓存在曲率变化,法向矢量存在连续变化,即齿廓竖直切线倾角γ连续变化.齿顶齿廓曲率变化决定了倾角的变化范围.因此,需合理设计 v及γB,使得齿廓能够连续啮合且得到尽可能大的共轭存在角度.
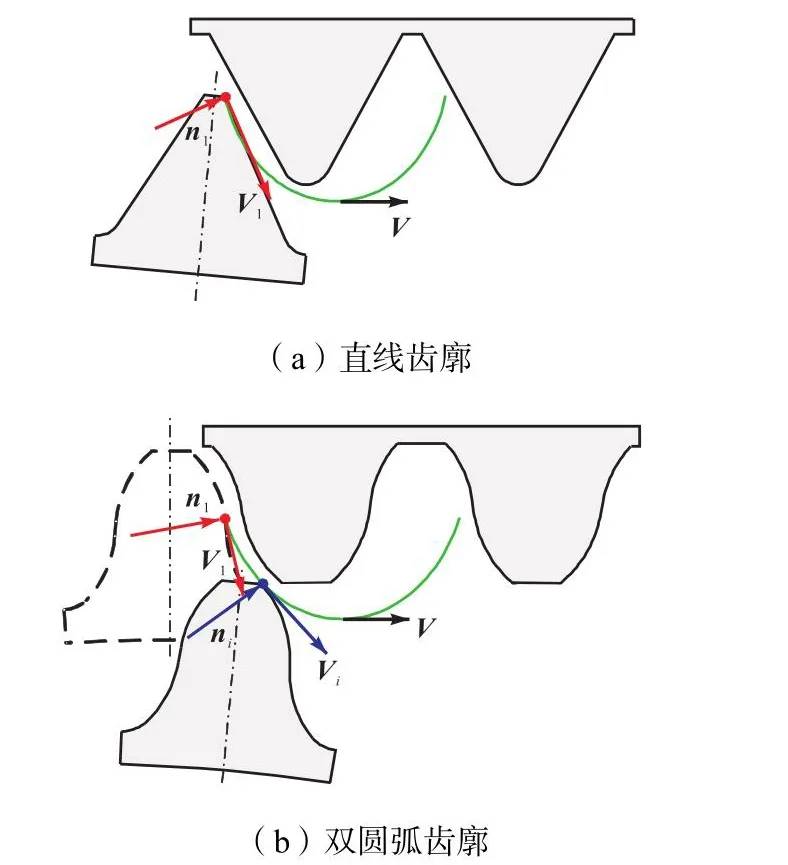
图6 柔轮齿廓法矢量与齿顶的速度矢量Fig.6 Normal vector of flexspline tooth profile and velocity vector of tooth tip
如图7所示,设竖直方向与齿廓切线的夹角为倾角γ,与速度矢量的夹角为 β.β的最大值为 90°,最小值βmin发生在公切点B处,有
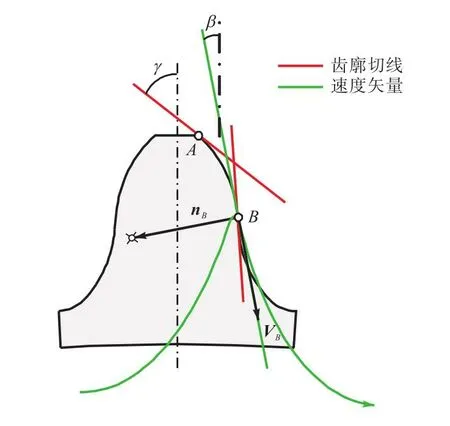
图7 齿廓倾角γ 与速度矢量夹角β 的定义Fig.7 Definition of tooth profile obliquity angle γand velocity vector inclination angle β
式中:jf为坐标系 Ofxfyf中 yf方向的单位矢量;VB由式(23)得到.
为满足齿顶齿廓均存在共轭解,倾角γ需大于速度矢量最小夹角βmin,即连续共轭条件
式中倾角γ最大值对应齿廓齿顶点处,且小于 90°,最小值对应齿廓公切点处,则式(27)也可表示为
由式(12)可知,公切线倾角γB主要由最大切向位移量vm决定,为此需要引入系数v*,对最大切向位移进行适当调整,有
式中v.*∈(0,1]
3.4 共轭齿廓求解
柔轮啮合端坐标系 Ofxfyf下的柔轮齿廓曲线RAB与法线nAB在刚轮坐标系 Ocxcyc下表示为
式中
采用改进运动学法求共轭齿廓[10],设Vc为共轭齿廓啮合点在 Ocxcyc坐标系下的相对速度矢量,表达式为
共轭齿廓的啮合方程为
B矩阵不包含任何共轭齿廓曲线的几何参数,只包含相对运动参数φ,简化了共轭齿廓的求解过程.
4 齿廓参数设计与啮合特性分析
4.1 设计算例
为验证本文双圆弧齿廓设计方法的有效性,分别以两种速比(i=80、100)参数为例,选用标准椭圆凸轮波发生器,给定柔轮中线半径rm=40.6400mm,模数m=0.4064,取最大径向变形量w0等于模数m,柔轮齿顶高取0.8m,齿根高取1.2m,齿厚比取1.2.
对柔轮进行运动分析,根据式(25)及柔轮中线方程,求解用于补偿基准直线的切向位移量 vm=30μm.根据式(26)计算出一个运动周期内的夹角 β的变化及最小值,如图8所示.
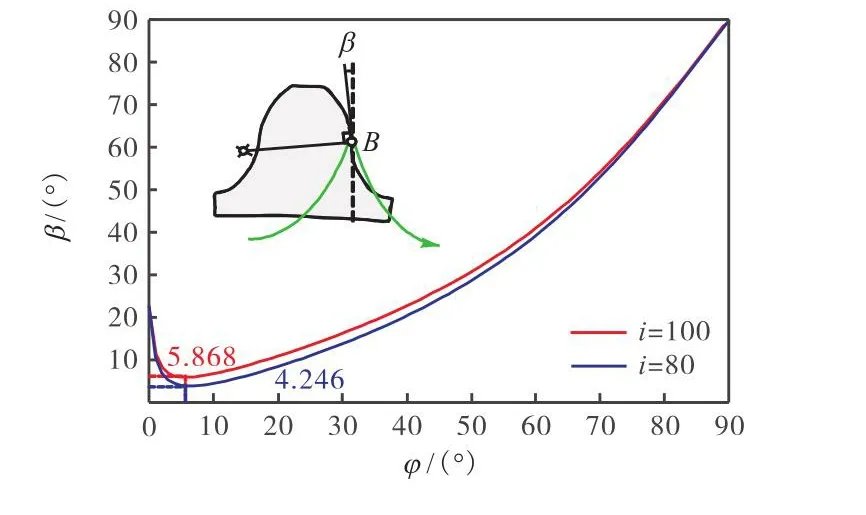
图8 一个周期内β随φ的变化Fig.8 Variations of β varies with φ in one cycle
根据式(33)求解共轭齿廓,得到共轭区间角度 φ随v*与α变化的等高线.为保证齿顶齿廓满足连续共轭解,v*和α的选取应满足式(28),即参数的可行域,如图9灰色区域所示,由图可知,随着 v*的增大,共轭区间不断增大,但可行域变小,随着α的增大,共轭区间不断增大,但可行域变大.参照文献[11]选取参考值α=28.6°,为获得较大的共轭区间,v*分别选取0.65、0.60,设计柔轮齿廓,并对刚轮齿廓进行包络拟合,齿廓参数如表2所示.
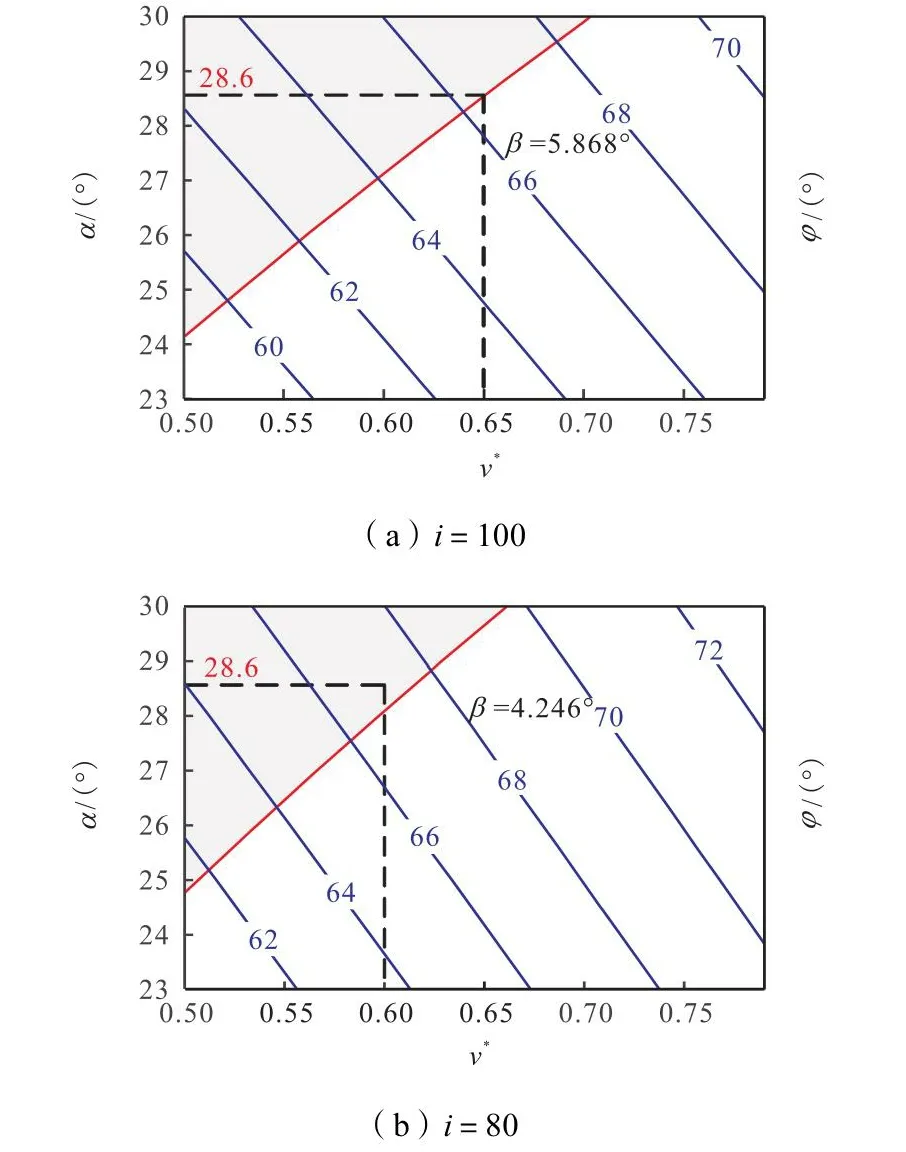
图9 共轭存在角度φ随v*与α 变化Fig.9 Contour map of φ varies with v* and α

表2 柔轮与刚轮齿廓参数Tab.2 Tooth parameters of flexspline and circular spline
4.2 啮合特性分析
为更直观分析柔轮齿相对刚轮的运动状态,以i=100为例,根据式(20),计算柔轮齿相对刚轮从啮入到啮出的相对运动轨迹如图10所示.由图10可知,啮合过程无干涉现象,啮合侧隙均匀.
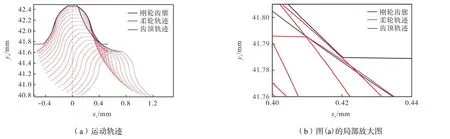
图10 柔轮齿运动轨迹Fig.10 Motion trajectory of flexspline tooth
根据设计完成的柔轮、刚轮齿廓参数求解共轭存在方程,得到共轭存在区间如图11所示,并利用文献[13]所提出的侧隙计算方法,对柔轮齿与刚轮齿在半个啮合周期内(φ∈[0,π/2])的啮合侧隙分布情况进行分析,如图11所示,齿廓在整个共轭存在区间内能够实现连续共轭啮合,啮出角度高达 68.6162°.由图12可知,啮合过程中侧隙δ始终大于0,无齿廓干涉,且理论最大侧隙不超过 2.5μm,能够较好地满足工程需要.
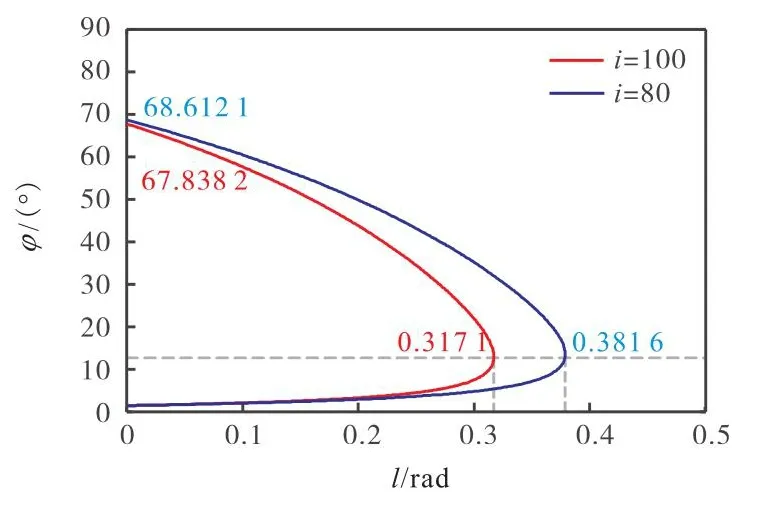
图11 齿廓共轭存在区间Fig.11 Existing conjugate domain of tooth profile
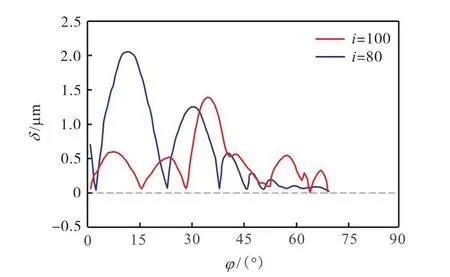
图12 齿廓侧隙分布Fig.12 Backlash distribution of tooth profile
4.3 有限元仿真验证
在有限元分析软件中模拟波发生器与柔轮的装配过程,检验柔轮变形后柔轮齿与刚轮齿的啮合侧隙及应力分布.选取表2中速比100的齿廓参数,设置柔轮壁厚 1.2mm,轴向宽度 2mm,将柔轮简化为齿圈薄壁圆环,波发生器简化为柔性轴承外圈圆环[19].
给定柔轮材料为42CrMo,弹性模量为205GPa,泊松比为 0.28,密度为 7.85×103kg/m3;刚轮为QT800,弹性模量为 150GPa,泊松比为 0.25;波发生器为 45号钢,弹性模量为 200GPa,泊松比为 0.30.在 ANSYS平台,以扫掠划分形式划分网格,采用六面体单元,刚轮、柔轮与波发生器的网格尺寸分别设置为 0.20mm、0.05mm、0.05mm,单元总数 568880.有限元仿真模型如图13所示.
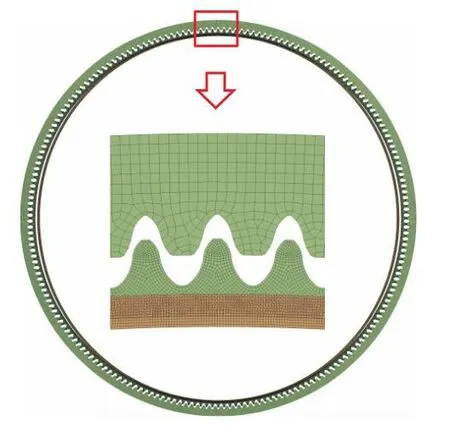
图13 装配前谐波齿轮有限元模型Fig.13 FEA model of the harmonic drive before assembly
设置柔轮内壁与波发生器外壁表面接触为非线性摩擦接触,摩擦系数 0.05,选用增广拉格朗日算法计算得到刚柔轮的径向变形分布云图如图14所示.图14中,最大径向位移分布在长轴区域,最小值出现在短轴区域附近,单侧共轭存在角度近 68.31°,单侧存在37对共轭齿.
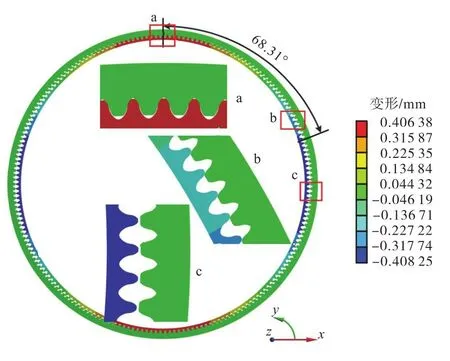
图14 径向变形分布云图Fig.14 Distribution of radial deformation
柔轮装配后的等效应力分布云图如图15所示,显示结果隐藏波发生器.由图15可知,空载下柔轮长轴端与短轴端轮齿齿根部分承受最大应力,应力沿中性线两端递减,在距长轴端 30°~45°处有应力最小值.
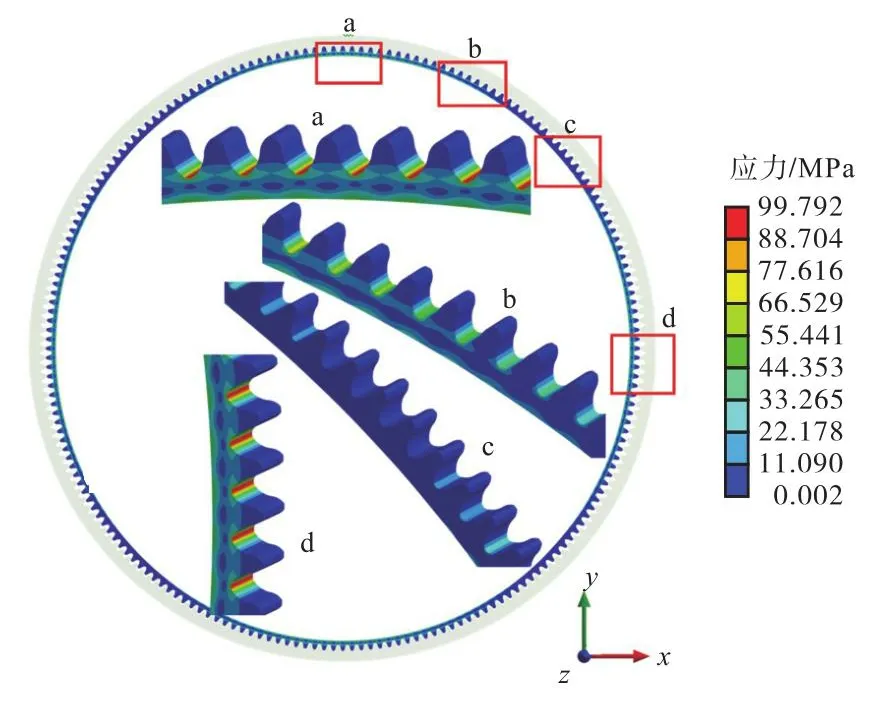
图15 柔轮的等效应力分布Fig.15 Von Mises stress distribution of flexspline
对比有限元仿真与数值分析结果,分别如图14、图16所示.其中,图16根据等分弧长分布法计算得到[12],结果显示存在 68.40°的啮合区间,单侧共轭齿对数为 38对,与图14结果(68.31°及单侧 37对)比较存在少量差异.计算有限元仿真结果的齿侧间隙,与理论侧隙值对比如图17所示,图中侧隙最大值小于 10μm,整体误差也稍大于理论侧隙值,这是由于有限元仿真计及了柔轮在波发生器作用下的几何接触和薄壳产生的微小弹性变形等因素,而理论模型忽略了柔轮的弹性变形.
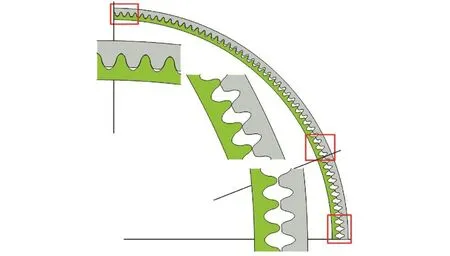
图16 理论啮合模型Fig.16 Theoretical meshing model
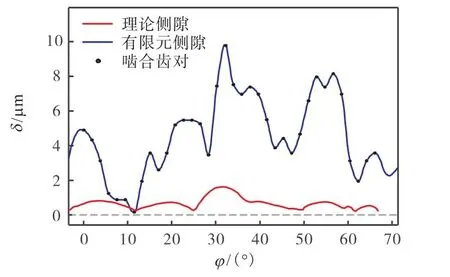
图17 理论与有限元的侧隙值对比Fig.17 Comparison of backlash distribution between theoretical value and FEA value
为更精确地验证柔轮变形量,从图14中提取1/4柔轮中性线上 200个采样点的径向变形量与周向变形量,与柔轮的解析变形结果进行对比,如图18所示.图中,径向变形量最大误差小于 1μm,周向变形量最大误差小于 11μm,整体误差能够满足工程需要,验证了本文解析模型的有效性.
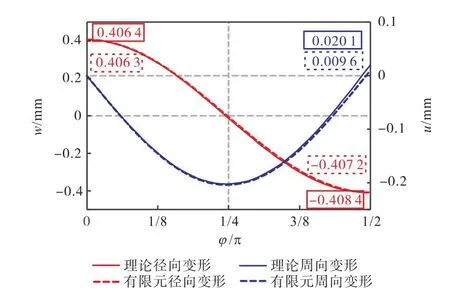
图18 理论与有限元的径向/周向变形量对比Fig.18 Comparison of radial and circumferential deformation between theoretical value and FEA value
5 结 论
针对现有谐波齿廓表征参数过多、设计柔度不足及设计参数之间关联度较低的问题,本文提出一种考虑柔轮齿相对运动轨迹的双圆弧齿廓设计方法,经有限元仿真分析验证方法的有效性,得到如下结论.
(1) 分析 2种运动模式下的柔轮齿廓公切点的运动轨迹:固定刚轮,获取柔轮齿相对刚轮齿的运动轨迹和速度矢量函数;固定柔轮,获得最大切向位移用于设计双圆弧齿廓,有效地将轮齿变形尺度与齿廓参数设计结合起来.
(2) 提出了一种双圆弧齿廓参数设计方法,设计的共轭齿廓可实现连续啮合且不存在干涉,具有较大的共轭存在区间,共轭存在角度为 68.31°,理论齿侧间隙小于2.5μm.
(3) 当齿厚比和分度圆给定时,柔轮齿顶圆弧的凹凸程度是影响共轭存在区间的主要因素,共轭区间随圆弧补偿系数v*和名义压力角α的增大而增大.
