在线教学平台生态系统演化博弈模型构建及稳定性研究
2023-03-14郑月龙罗洪川张春容
张 露,郑月龙,罗洪川 ,张春容,杨 琴
(1.西南大学 新闻传媒学院, 重庆 400715; 2.重庆工商大学 艺术学院, 重庆 400067; 3.重庆工商大学 工商管理学院, 重庆 400067;4.西南大学 西南民族教育与心理研究中心, 重庆 400715;5.西南大学 商贸学院, 重庆 400715; 6.重庆市教育委员会 招生考试管理处, 重庆 400020)
0 引言
自2013年可汗学院、Coursera等国际知名在线教学平台设立以来,在线教学得到了迅速发展[1]。目前,利用人工智能、大数据等现代信息技术推动教育教学改革已成为学校教学改革的重要抓手,2020年开始的“停课不停学、停课不停教”更加凸显了在线教学的价值。而在线教学质量的好坏,受到在线教学参与者如教师、在线教学平台及学生等互动的影响,在线教学本质上是知识传递和交换的过程,实现知识有效传递和交换及教学质量提升的可持续发展是在线教学活动的根本。为此,借鉴平台生态系统思想,以在线教学知识交互为研究对象,探究在线平台生态系统的演化机理,助力在线教学高质量发展。
目前,在线教学领域的研究受到国内外学者的青睐。首先,关于在线教学的研究,徐亚倩等[2]指出在线教学呈现开放、联通和复杂的特点。随着环境的不断优化,个性化和公平性越来越好,在线教学已成为各级各类学校课堂教学的重要补充形式[3]。Mansbach等[4]指出教师在线教学面临应对信息不对称导致陌生感、疏离感、孤独感、失控感和挫败感的挑战;需要在课程设计与开发、课程实施与评估等取得平衡[5]。为此,增强教师“项目式学习、基于问题的学习、小组合作学习”等能力及“参与式和任务式”在线学习评价能力[6],可一定程度上缓解教师在线教学面临的挑战。此外,在线教学中教师也面临一对一交互和沟通协调管理能力的挑战[4,7],教师花费最多时间的是评估学习者学习目标达成的情况,提供作业指导和反馈等[8]。其次,关于平台生态系统的研究,Jacobides等[9]区分了商业、创新及平台生态系统,指出平台生态系统就像是平台所有者、补充者和最终用户相互协调的社区[10]。王节祥等[11]将平台参与者视为具有能动性个体,参与者在具有强互补性的同时需要降低对平台的依赖性才能提升绩效。Adner等[12]将生态系统看作是相互作用多边合作伙伴为实现共同核心价值主张而进行协调的结构;是以平台所有者、互补者、用户之间的互动为基础形成的经济共同体[13-14]。然而,将在线教学和平台生态系统结合起来的研究却很少,王康[15]结合武汉市“空中课堂”实际,指出在线教学生态系统应包括教学主体、教学环境、教学资源和活动,且共同支撑在线教学生态系统良性发展;许晓旭[16]探讨了“互联网+”背景下的线上生态课堂模式的构建与实施,旨在充分发挥在线教学的优点。
然而,在线教学涉及在线平台及其关联的教师和学习者构成一种相互依赖关系,构成了平台竞争优势的关键来源[17],实践中各参与主体构成了一种互动博弈关系,通过构建在线教学平台生态系统助力这种关系良性发展。本文主要创新点是将在线教学与平台生态系统内涵相结合,将教师泛化为知识供给者,学习者泛化为知识需求者,将知识供给者、知识需求者及在线教学平台三者看作为基于收益权衡的一个随时间变化的动态演化系统,建立在线教学平台生态系统的三方演化博弈,借以探讨知识供给方(如教师)、知识需求方(如学生)及在线教学平台三方行为策略演化过程、影响因素及演化机理。通过研究丰富在线教学平台生态系统的相关研究,为在线教学实践提供参考。
1 模型构建与求解
1.1 演化博弈与建模
20 世纪70年代是演化博弈理论迎来发展的关键期,表现为Smith[18]及Smith等[19]提出演化稳定策略(evolutionary stable strategy,ESS)及Taylor等[20]提出复制者动态,自此演化博弈有了明确的研究目标,即通过复制者动态选择机制寻找博弈的ESS。根据Taylor等[20]的研究,可将复制者动态方程表示为:
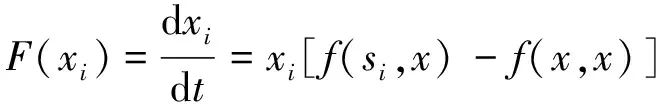
(1)
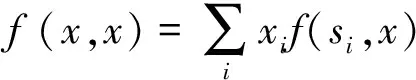
根据复制动态方程稳定性原理[21],当F(xi)=0且F′(xi)<0时,则xi点对应的策略即是博弈的ESS。演化博弈以参与人有限理性为假设,这意味着均衡不是一蹴而就的,而是博弈参与方通过学习和试错不断调整和改进,式(1)即体现了这一思想。在线教学各参与方策略选择也是一个动态演化过程,即起初各主体并不能确定哪种策略能给自己带来更大收益,需通过不断学习、试错、模仿来调整自身策略,逐渐实现ESS。据此,本文通过建立三方演化博弈模型对在线教学平台生态系统展开研究。
1.2 基本假设
1) 有限理性。在线教学生态系统参与方均为有限理性的,即由于信息不对称及参与主体自身知识等限制,并不知道自己选择的策略是否是对自己最好的,会随着时间推进,不断学习、调整和优化自身的策略,进而实现局部稳定状态。
2) 策略空间。知识供给方策略空间为{参与,深度参与},深度参与指知识供给方利用在线平台从事教学活动的同时,还进行课程开发、项目合作、专家咨询等,以x(0≤x≤1)的概率选择参与和1-x的概率选择深度参与;知识需求方策略空间为{学习,深度学习},深度学习指知识需求方使用在线教学平台基本功能之外,还进行学分认证、课程学习指导等学习活动,以y(0≤y≤1)的概率选择学习和1-y的概率选择深度学习;在线教学平台策略空间为{维持运营,积极开发},积极开发指在维持运营的基础上积极开发各类课程、项目及社群等,以z(0≤z≤1)的概率选择维持运营和1-z的概率进行积极开发。
3) 相关成本。知识供给方选择参与和深度参与均会付出成本,如投入时间和精力、梳理知识和准备资料,分别用Cs和Cs1表示,满足Cs
4) 各方收益。知识供给方深度参与时基本收益分别为Bs和Bs1,Bs
1.3 模型构建
根据假设,可得在线教学平台生态系统的博弈支付矩阵,如表1所示。

表1 在线教学平台生态系统博弈支付矩阵
根据表1,可得知识供给方选择参与策略时的期望支付Ux(1)为:
Ux(1)=yz[sBs-s1Bs-sdsBs+s1dsBs]+y[s1Bs-s1dsBs]+
z[sdsBs-s1dsBs-αCs+α1Cs]+[s1dsBs-α1Cs]
(2)
知识供给方选择深度参与策略时的期望支付Ux(0)为:
Ux(0)=yz[sBs1-s1Bs1-sdsBs1+s1dsBs1]+y[s1Bs1-s1dsBs1]+
z[sdsBs1-αCs1-s1dsBs1+α1Cs1-S]+[s1dsBs1-α1Cs1+S]
(3)
知识供给方平均期望支付UX为:
UX=xUx(1)+(1-x)Ux(0)
(4)
于是,可得知识供给方的复制动态方程为:
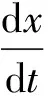
y(s1(Bs1-Bs)(ds-1))+z(ds(Bs1-Bs)(s1-s)-(α1-α)(Cs1-Cs)+S)+
s1ds(Bs-Bs1)+α1(Cs1-Cs)-S]
(5)
知识需求方选择学习策略时的期望支付Uy(1)为:
Uy(1)=x[Bd-sdBd]+z[β1Cd-βCd]+[sdBd-β1Cd]
(6)
知识需求方选择深度学习策略时的期望支付Uy(0)为:
Uy(0)=x[σBd-sdσBd]+z[β1Cd1-βCd1-D]+[sdσBd-β1Cd1+D]
(7)
数字金融服务机构平均期望支付UY为:
UY=yUy(1)+(1-y)Uy(0)
(8)
进而,可得知识需求方的复制动态方程为:

z((β-β1)(Cd1-Cd)+D)+sdBd(1-σ)+β1(Cd1-Cd)-D]
(9)
在线教学平台选择维持运营策略时的期望支付Uz(1)为:
Uz(1)=xy[dmΔBe-ΔBe]+x[-dmΔBe]+y[Bm+ΔBe-dm(Bm+ΔBe)]+
[dm(Bm+ΔBe)-Cm]
(10)
在线教学平台选择积极参与策略时的期望支付Uz(0)为:
Uz(0)=xy[dmΔBe1-ΔBe1]+x[-dmΔBe1]+y[Bm1+ΔBe1-dm(Bm1+ΔBe1)]+
dm(Bm1+ΔBe1)-Cm1
(11)
在线教学平台平均期望支付为UZ为:
UZ=zUz(1)+(1-z)Uz(0)
(12)
同理,可得在线教学平台的复制动态方程为:
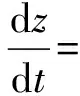
y[(dm-1)(Bm1-Bm+ΔBe1-ΔBe)]+[dm(Bm+ΔBe-Bm1-ΔBe1)+Cm1-Cm]]
(13)
1.4 稳定性分析
知识供给方的复制动态方程为:
F(x)=x(1-x)[yz((s1-s)(Bs1-Bs)(1-ds))+y(s1(Bs1-Bs)(ds-1))+
z(ds(Bs1-Bs)(s1-s)-(α1-α)(Cs1-Cs)+S)+
s1ds(Bs-Bs1)+α1(Cs1-Cs)-S]
(14)
对F(x)求导得:
F′(x)=(1-2x)[y((z(s1-s)-s1)(Bs1-Bs)(1-ds))+s1ds(Bs-Bs1)+α1(Cs1-Cs)-S+
z(ds(Bs1-Bs)(s1-s)-(α1-α)(Cs1-Cs)+S)]
(15)

知识需求方的复制动态方程为:
F(y)=(1-y)[x((σ-1)(sd-1)Bd)+z((β-β1)(Cd1-Cd)+D)+
sdBd(1-σ)+β1(Cd1-Cd)-D]
(16)
对F(y)求导得:
F′(y)=(1-2y)[x((σ-1)(sd-1)Bd)+z((β-β1)(Cd1-Cd)+D)+
sdBd(1-σ)+β1(Cd1-Cd)-D]
(17)
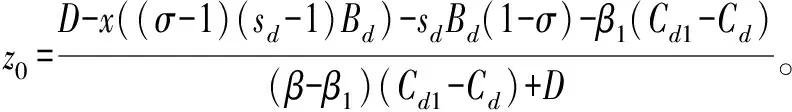
在线教学平台的复制动态方程为:
F(z)=[xy((ΔBe1-ΔBe)(1-dm))+xdm(ΔBe1-ΔBe)+y[(dm-1)(Bm1-Bm+ΔBe1-ΔBe)]+
[dm(Bm+ΔBe-Bm1-ΔBe1)+Cm1-Cm]]
(18)
对F(z)求导得:
F′(z)=(1-2z)[x(y((ΔBe1-ΔBe)(1-dm))+dm(ΔBe1-ΔBe))+
y[(dm-1)(Bm1-Bm+ΔBe1-ΔBe)]+[dm(Bm+ΔBe-Bm1-ΔBe1)+Cm1-Cm]]
(19)

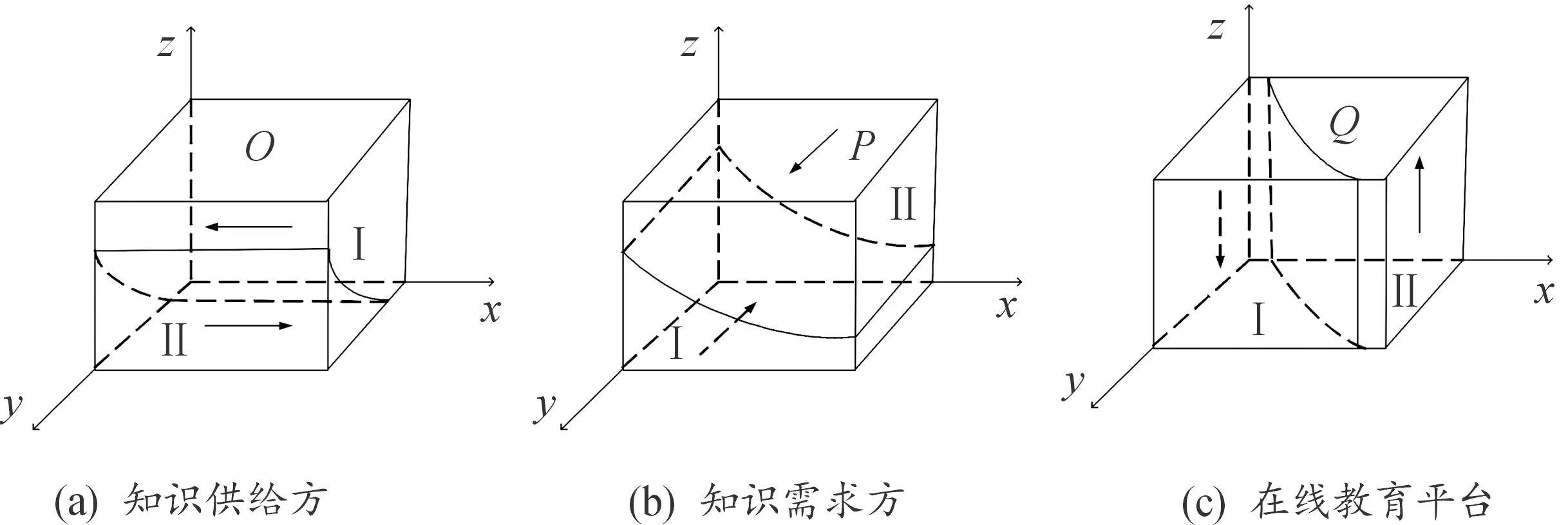
图1 三方策略演化相位图
2 三方演化博弈平衡点稳定性分析
在线教学平台生态系统三方演化博弈平衡点稳定性可通过以下方程得到:

(20)
存在8个平衡点:E1(0,0,0),E2(0,0,1),E3(0,1,0),E4(1,0,0),E5(1,1,0),E6(1,0,1),E7(0,1,1),E8(1,1,1)及混合平衡点为E9(x*,y*,z*),若满足 0 (21) 式中: F11=(1-2x)[yz((s1-s)(Bs1-Bs)(1-ds))+y(s1(Bs1-Bs)(ds-1))+ z(ds(Bs1-Bs)(s1-s)-(α1-α)(Cs1-Cs)+S)+s1ds(Bs-Bs1)+α1(Cs1-Cs)-S] F12=x(1-x)[z(s1-s)(Bs1-Bs)(1-ds)+s1(Bs1-Bs)(ds-1)] F13=x(1-x)[y(s1-s)(Bs1-Bs)(1-ds)+ds(Bs1-Bs)(s1-s)-(α1-α)(Cs1-Cs)+S] F21=y(1-y)(σ-1)(sd-1)Bd F22=(1-2y)[x((σ-1)(sd-1)Bd)+z((β-β1)(Cd1-Cd)+D)+sdBd(1-σ)+ β1(Cd1-Cd)-D] F23=y(1-y)[(β-β1)(Cd1-Cd)+D] F31=z(1-z)[y(ΔBe1-ΔBe)(1-dm)+dm(ΔBe1-ΔBe)] F32=z(1-z)[x(ΔBe1-ΔBe)(1-dm)+(dm-1)(Bm1-Bm+ΔBe1-ΔBe)] F33=(1-2z)[xy((ΔBe1-ΔBe)(1-dm))+xdm(ΔBe1-ΔBe)+ y[(dm-1)(Bm1-Bm+ΔBe1-ΔBe)]+[dm(Bm+ΔBe-Bm1-ΔBe1)+Cm1-Cm]] 以平衡点E1(0,0,0)为例,其雅可比矩阵可以简写为: (22) 式(22)的特征值分别为λ1=s1ds(Bs-Bs1)+α1(Cs1-Cs)-S,λ2=sdBd(1-σ)+β1(Cd1-Cd)-D,λ3=dm(Bm+ΔBe-Bm1-ΔBe1)+Cm1-Cm)。同理得其他平衡点的特征值,如表2所示。 表2 各平衡点对应雅可比矩阵的特征值 不失一般性,将研究情形分为四类,以考察系统演化的稳定性,如表3所示。 表3 各平衡点对应雅可比矩阵的特征值符号判断 情形1:满足条件E1>0且F1>0,当G4>0时,平衡点E1(0,0,0)为系统的ESS(情形S1-1),当G4<0时,平衡点E2(0,0,1)为系统的ESS(情形S1-2)。 情形1中,E1>0表示知识供给方在选择深度参与策略时所取得的支付始终大于选择参与策略,因此知识供给方将选择深度参与策略。F1>0表示知识需求方在选择深度学习策略时所取得的支付始终大于其选择学习策略,因此知识需求方将选择深度学习策略。此时,若在线学习平台在积极开发时取得支付更大,即满足条件G4>0,则E1(0,0,0)为系统的ESS,即深度参与、深度学习、积极开发策略组合,否则E2(0,0,1)为系统ESS,即深度参与、深度学习、维持运营策略组合。 情形2:满足条件E1>0且F1<0,当G3>0时,若F4>0,则平衡点E1(0,0,0)为系统的ESS(情形S2-1),否则E3(0,1,0)为系统的ESS(情形S2-2);当G4<0时,若F2>0,则平衡点E2(0,0,1)为系统的ESS(情形S2-3),否则E7(0,1,1)为系统的ESS(情形S2-4)。 情形2中,知识供给方始终选择深度参与策略。F1<0表示知识需求方在选择深度学习策略时所取得的基本支付小于其选择学习策略,其策略选择受到知识供给方及在线教学平台的影响。G3>0表示在知识供给方选择深入参与策略时,在线教学平台选择积极开发支付大于维持运营,在线教学平台将选择积极开发策略,此时若F4>0,表示在知识供给方深入参与以及在线教学平台积极开发的作用下,知识需求方选择深度学习策略所取得的支付大于选择学习策略,E1(0,0,0)为系统的ESS,否则E3(0,1,0)为系统的ESS,对应于深度参与、学习、积极开发策略组合。G4<0表示在线教学平台选择积极开发策略支付始终小于选择维持运营策略,其将选择维持运营策略,此时若F2>0,表示在知识供给方深入参与的作用下,知识需求方选择深度学习策略所取得的支付大于选择学习策略,E2(0,0,1)为系统的ESS,否则E7(0,1,1)为系统的ESS,即深度参与、学习、维持运营策略组合。 情形3:满足条件E1<0且F1>0,当G2>0时,若E4>0,则平衡点E1(0,0,0)为系统的ESS(情形S3-1),否则E4(1,0,0)为系统的ESS(情形S3-2);当G4<0时,若E2>0,则平衡点E2(0,0,1)为系统的ESS(情形S3-3),否则E6(1,0,1)为系统的ESS(情形S3-4)。 情形3中,E1<0表示知识供给方在选择深度参与策略时所取得的基本支付小于其选择参与策略,其策略选择受到知识需求方及在线教学平台的影响。知识需求方将始终选择深度学习策略。G2>0表示在知识需求方选择深入参与学习时,在线教学平台选择积极开发支付大于维持运营,在线教学平台将选择积极开发策略,此时若E4>0,表示在知识需求方深入学习以及在线教学平台积极开发的作用下,知识供给方选择深度参与策略所取得的支付大于选择学习策略,E1(0,0,0)为系统的ESS,否则E4(1,0,0)为系统的ESS,即参与、深度学习、积极开发策略组合。G4<0表示在线教学平台选择积极开发策略支付始终小于选择维持运营策略,其将选择维持运营策略,此时若E2>0,表示在知识需求方深入参与的作用下,知识供给方选择深度参与策略所取得的支付大于选择学习策略,E2(0,0,1)为系统的ESS,否则E6(1,0,1)为系统的ESS,即参与、深度学习、维持运营策略组合。 情形4:满足条件E1<0且F1<0,当E3>0且G3>0时,若F4>0,则平衡点E1(0,0,0)为系统的ESS(情形S4-1),否则E3(0,1,0)为系统的ESS(情形S4-2);当E3>0且G4<0时,若F2>0,平衡点E2(0,0,1)为系统的ESS(情形S4-3);当E3<0且G1>0时,若F3>0,则平衡点E4(1,0,0)为系统的ESS(情形S4-4),否则E5(1,1,0)为系统的ESS(情形S4-5);当E3<0且G1<0时,平衡点E8(1,1,1)为系统的ESS(情形S4-6)。 情形4中,E1<0表示知识供给方在选择深度参与所取得的基本支付小于选择参与策略。F1<0表示知识需求方在选择深度学习策略所取得的基本支付小于其选择学习策略。此时E3>0表示知识供给方在在线教学平台选择积极开发作用下,深度参与策略所取得的支付大于参与策略;G3>0表示在线教学平台在知识供给方选择深度参与作用下,其选择积极开发策略所取得支付大于维持运营;若F4>0,表示知识需求方在知识供给方及在线教学平台选择优势策略的积极作用下,其选择深度学习的支付更大,此时E1(0,0,0)为系统的ESS,否则E3(0,1,0)为系统的ESS。情形4其余情况做类似讨论分析,不再赘述。其中: E1:s(Bs1-Bs)-α(Cs1-Cs),E2:sds(Bs1-Bs)-α(Cs1-Cs) E3:s1(Bs1-Bs)-α1(Cs1-Cs)+S,E4:s1ds(Bs1-Bs)-α1(Cs1-Cs)+S F1:Bd(σ-1)-β(Cd1-Cd),F2:sdBd(σ-1)-β(Cd1-Cd) F3:Bd(σ-1)-β1(Cd1-Cd)+D,F4:sdBd(σ-1)-β1(Cd1-Cd)+D G1:(Bm1-Bm)-(Cm1-Cm),G2:dm(Bm1-Bm)-(Cm1-Cm) G3:(Bm1-Bm+ΔBe1-ΔBe)-(Cm1-Cm),G4:dm(Bm1+ΔBe1-Bm-ΔBe)-(Cm1-Cm) 为验证演化稳定性分析的有效性,利用Matlab进行数值仿真。满足相关假设条件时设s=1.2,s1=1.3,Bs=2,Bs1=3,α=0.6,α1=0.5,Cs=1,Cs1=7,ds=1.2,Bd=2,σ=1.5,β=0.6,β1=0.5,Cd=7,Cd1=8,S=1.5,D=1,sd=1.3,Bm=2,Bm1=4,ΔBe=0.5,ΔBe1=0.6,Cm=8,Cm1=10.45,dm=1.2。如无特别说明,在研究某一参数影响时其他参数保持不变。 知识供给收益差额Bs1-Bs、平台收益差额Bm1-Bm及平台额外收益差额ΔBe1-ΔBe对系统演化的影响如图2所示。 图2 收益差额对系统演化的影响曲线 如图2(a)所示,当Bs1-Bs由0.1增加至3.8,系统ESS由E6(1,0,1)逐渐演化至E1(0,0,0),可知随着供给收益差额的增加,知识供给方策略选择由参与演化至深度参与,在线教学平台策略选择由维持运营演化至积极开发。如图2(b)所示,当Bm1-Bm由2增加至4,系统ESS由E8(1,1,1)逐渐演化至E3(0,1,0),可知随着平台收益差额的增加,在线教学平台策略选择由维持运营演化至积极开发,知识供给方策略选择由参与演化至深度参与。平台额外收益差额ΔBe1-ΔBe与平台收益差额Bm1-Bm影响类似,不再赘述。由此可得: 结论1供给收益差额、平台收益差额及平台额外收益差额对知识供给方及在线教学平台策略选择有积极影响,且上述收益差额也同时对对方策略选择产生积极影响。 根据结论1,由于当知识供给收益差额增大时,提升了知识供给方参与积极性,为了获取更多收益平台,将选择积极开发策略;当平台收益差额增大时,在线教学平台将采取积极开发策略,此时知识供给方也可通过平台获取更多的收益,促进其深度参与平台知识供给。 1) 在线教学平台对知识供给方收益的影响系数s、s1及深度学习收益影响系数σ对系统演化的影响如图3所示。 图3 收益影响系数对系统演化的影响曲线 以s1为例,如图3(a)所示,当s1由1.3增加至8.7,系统ESS由E6(1,0,1)逐渐演化至E1(0,0,0),可知随着在线教学平台对知识供给方收益的影响系数的增加,知识供给方策略由参与演化至深度参与,在线教学平台策略由维持运营演化至积极开发。如图3(b)所示,当σ由1.5增加至2.5,系统ESS由E8(1,1,1)逐渐演化至E1(0,0,0),可知随着深度学习收益影响系数增加,知识供给方策略由参与演化至深度参与,知识需求方策略由学习演化至深度学习,在线教学平台策略选择由维持运营演化至积极开发。由此可得: 结论2在线教学平台对知识供给方收益的影响系数对知识供给方及在线教学平台策略选择有积极影响,深度学习收益影响系数对知识供给方、知识需求方及在线教学平台三方策略选择均有积极影响。 根据结论2,良好的在线教学平台可促进知识供给方参与积极性,使其选择深度参与策略的概率增加。而深度学习收益影响系数是在线教学平台系统中较为重要的系数,直接影响到知识的供给、吸收及平台的维持,助力在线教学平台生态良好运行。 2) 知识供给方深度参与时对知识需求方的影响系数sd,知识需求方深度学习时对知识供给方和在线教学平台收益的影响系数ds、dm对系统演化的影响如图4所示。 图4 收益影响系等数对系统演化的影响曲线 如图4(a)所示,当sd由1.3增加至4.3,系统ESS由E8(1,1,1)逐渐演化至E1(0,0,0),可知随着知识供给方深度参与时对知识需求方的影响系数的增加,知识供给方策略由参与演化至深度参与,知识需求方策略由学习演化至深度学习,在线教学平台策略由维持运营演化至积极开发。如图4(b)所示,当ds由1.2增加至3.8,系统ESS由E6(1,0,1)逐渐演化至E1(0,0,0),可知随着知识需求方深度学习时对知识供给方的影响系数的增加,知识供给方策略选择由参与演化至深度参与,在线教学平台策略选择由维持运营演化至积极开发。如图4(c)所示,当dm由1.2增至3.5,系统ESS由E8(1,1,1)逐渐演化至E3(0,1,0),可知随着知识需求方深度学习时对在线教学平台的影响系数的增加,在线教学平台策略选择由维持运营演化至积极开发,知识供给方策略由参与演化至深度参与。由此可得: 结论3随着知识供给方深度参与时对知识需求方影响系数的增加,知识供给方、知识需求方、在线教学平台策略分别演化至深度参与、深度学习、积极开发;随着知识需求方深度学习时对知识供给方的影响系数的增加,知识供给方、在线教学平台策略选择分别演化至深度参与、积极开发,而对在线教学平台影响系数的增加,在线教学平台、知识供给方策略演化至积极开发、深度参与。 根据结论3,在线教学平台生态系统参与方收益影响系数相互影响其他方策略选择,参与各方应理解影响系数影响范围及作用方向,助力在线教学平台生态系统形成和发展。 知识供给成本差额Cs1-Cs、知识需求成本差额Cd1-Cd及平台成本差额Cm1-Cm对系统演化的影响如图5所示。 图5 成本差额对系统演化的影响曲线 如图5(a)所示,当Cs1-Cs由2增加至12,系统ESS由E1(0,0,0)逐渐演化至E6(1,0,1),可知随着知识供给成本差额的增加,知识供给方策略选择由深度参与演化至参与,在线教学平台策略选择由积极开发演化至运营维持。如图5(b)所示,当Cd1-Cd由1增加至3,系统ESS由E1(0,0,0)逐渐演化至E8(1,1,1),可知随着知识需求成本差额的增加,知识供给方策略选择由深度参与演化至参与,知识需求方策略选择由深度学习演化至学习,在线教学平台策略选择由积极开发演化至运营维持。如图5(c)所示,当Cm1-Cm由0.45增加至2.45,系统ESS由E3(0,1,0)逐渐演化至E8(1,1,1),可知随着平台成本差额增加,在线教学平台策略由积极开发演化至运营维持,知识供给方策略由深度参与演化至深度。由此可得: 结论4成本差额对在线教学平台生态系统博弈参与方策略选择有负向影响,且不同方的成本差额同样也影响到其他方的策略选择。 根据结论4,博弈参与方互动对在线教学平台生态系统运行具有重要影响,成本作为收益的减项,博弈参与方应该更好地控制选择积极策略时的成本,助力在线教学平台生态系统朝着更积极的方向演化。 平台维持运营及积极开发时对知识供给者成本的影响系数α和α1,平台维持运营及积极开发时知识需求方成本的影响系数β和β1对系统演化的影响如图6所示。 以α1为例,如图6(a)所示,当α1由0.01增加至0.45,系统ESS由E1(0,0,0)逐渐演化至E6(1,0,1),可知随着平台积极开发时对知识供给者成本影响系数的增加,知识供给方策略选择由深度参与演化至参与,在线教学平台策略选择由积极开发演化至运营维持。以β1为例分析平台积极开发时对知识需求方成本的影响系数对系统演化的影响,如图6(b)所示,当β1由0.01增加至0.5,系统ESS由E1(0,0,0)逐渐演化至E8(1,1,1),可知随着β1的增加,知识供给方策略选择由深度参与演化至参与,知识需求方由深度学习演化至学习,在线教学平台策略选择由积极开发演化至运营维持。由此可得: 图6 成本影响系数对系统演化的影响曲线 结论5成本影响系数对在线教学平台生态系统演化有负向影响,且各影响系数相互对其他方的策略选择产生消极影响。 分析平台奖励S、D对系统演化的影响,如图7所示。以S为例,当S由1.5增加至5.5,系统ESS由E6(1,0,1)逐渐演化至E1(0,0,0)。由此可得: 图7 平台奖励对系统演化的影响曲线 结论6随着在线教学平台奖励的增加,知识供给方策略由参与演化至深度参与,在线教学平台策略选择由运营维持演化至积极开发。 综合结论1至结论6可知,在线教学平台生态系统受到博弈参与方策略的相互影响,可从参与各方互动影响切入进行分析,如知识供给方深度参与时对知识需求方的影响,知识需求方深度学习时对知识供给方的影响等。同时,博弈方收益差额、成本差额及在线教学平台奖励的增加等也对在线教学平台生态系统良性运行有重要影响。通过厘清上述影响因素及机理,促使在线教学平台生态系统朝着良性状态(深度参与、深度学习、积极开发)演化。 借鉴平台生态系统思想,通过建立知识供给方、知识需求方及在线教学平台间的三方演化博弈模型,揭示了在线平台生态系统演化机理。结果发现:① 供给收益差额、平台收益差额及平台额外收益差额对知识供给方及在线教学平台策略选择有积极影响,也对对方策略选择有积极影响;成本差额对参与方策略选择有负向影响,且不同方成本差额同样也影响到其他方策略选择。② 随着知识供给方深度参与对知识需求方影响系数的增加,知识供给方、知识需求方、在线教学平台策略分别演化至深度参与、深度学习、积极开发;随着知识需求方深度学习对知识供给方影响系数增加,知识供给方、在线教学平台策略选择分别演化至深度参与、积极开发,而对平台影响系数增加,平台、知识供给方策略演化至积极开发、深度参与。③ 在线教学平台对知识供给方收益影响系数对知识供给方及平台策略选择有积极影响,深度学习收益影响系数对三方策略选择均有积极影响;成本影响系数对平台生态系统演化有负向影响,且各影响系数相互对其他方策略选择有消极影响;随着平台奖励增加,知识供给方、在线教学平台策略由参与、维持运营分别演化至深度参与、积极开发。 根据结论有如下启示。首先,就在线教学平台而言,在线教学平台作为知识供给方和知识需求方的纽带,对在线教学平台生态系统良性运行具有重要意义。为此,在线教学平台应为知识供求双方提供良好知识传递平台,引进高质量知识供给方及提供奖励等方式打造精品课程及项目,使知识供给方有收获,也为在线教学平台和知识需求方提供高质量知识池;其次,就知识供给方而言,通过深度参与贡献高质量知识,促进生态系统参与方策略分别朝着深度参与、深度学习、积极开发演化,通过团队协同等降低在线课程等项目开发成本,促进在线教学平台生态系统良性运行;最后,就知识需求方而言,通过信息交流和反馈为在线教学平台和知识供给方有的放矢地开发相关项目,知识需求方应去掉“凑合”的态度,深度参与在线教学学习活动,从需求端牵引博弈参与方选择深度参与、深度学习、积极开发策略,推进在线教学平台生态系统良性运行。 作为初步研究,本文可进一步考虑其他关联主体,如咨询机构、市场调研机构等对本文模型进行拓展,以丰富在线教学平台生态系统领域的研究。此外,未来还可以将知识需求者分为不同类型,如在校学生、技术人员及高层管理者等,通过引入他们的个性化需求,丰富现有博弈,更好地挖掘在线教学平台生态系统内在运行机理。

3 多主体仿真分析
3.1 收益差额对系统演化的分析

3.2 收益影响系数对系统演化的分析


3.3 成本差额对系统演化的分析
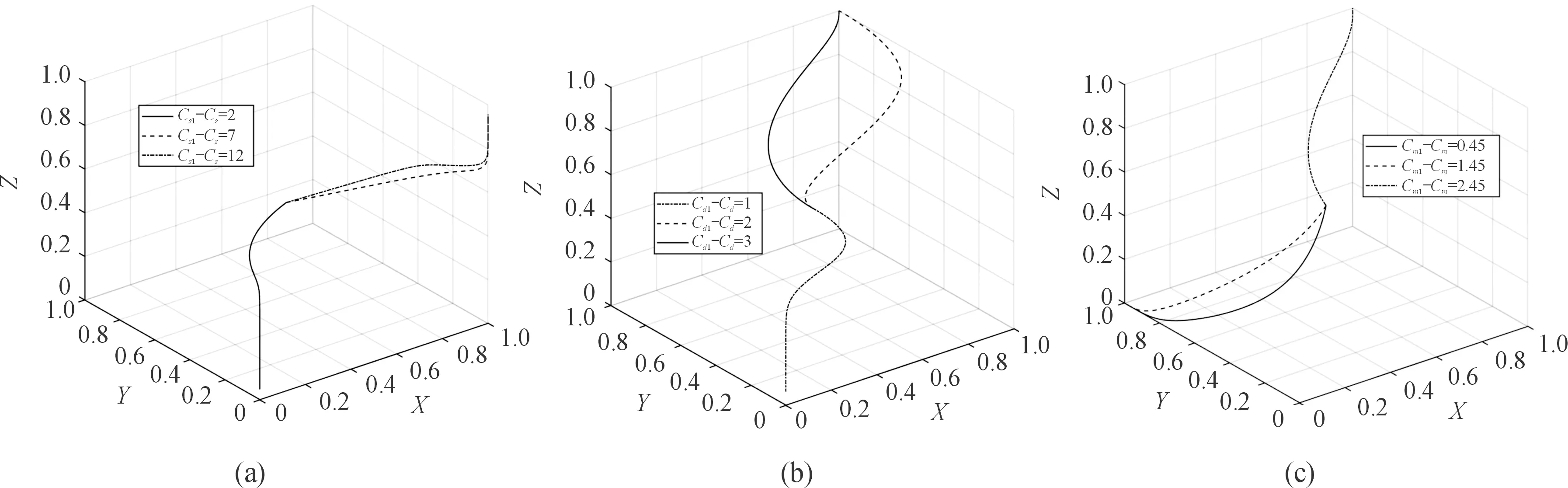
3.4 成本影响系数对系统演化的分析

3.5 平台奖励对系统演化的分析
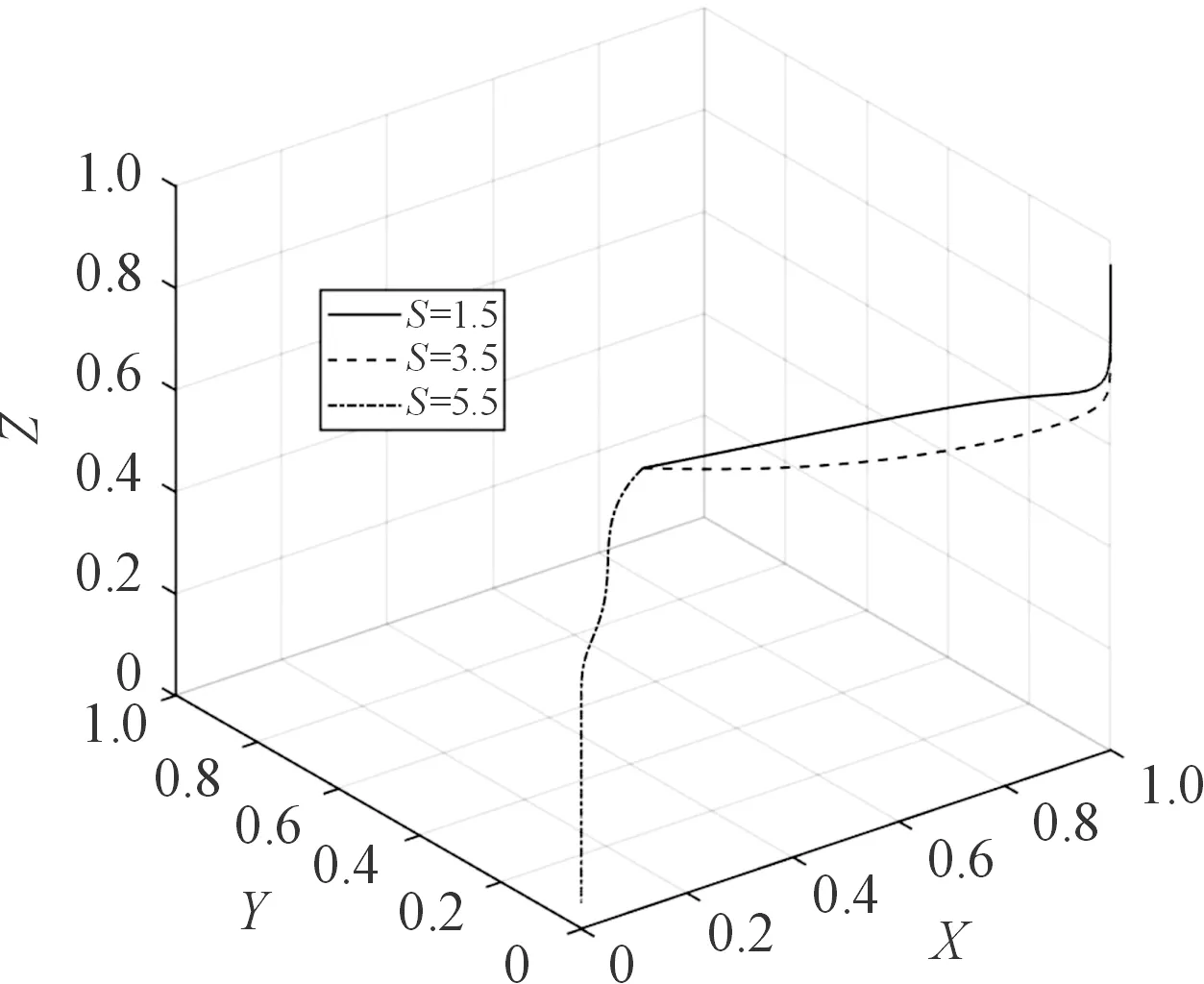
4 结论
