多源异构数据贝叶斯变权融合可靠性评估模型
2023-03-14程世娟张晓洁蒋玉婷
唐 莉,程世娟,张晓洁,蒋玉婷
(1.西南交通大学 数学学院, 成都 611756; 2.西南交通大学希望学院 基础部, 成都 610400)
0 引言
科技的不断进步和新型材料的不断出现,使产品的寿命越来越长,这些高长寿命产品在正常试验条件下在短时间内的失效数据较少,这些小样本携带的信息量不足以支撑传统的统计分析。很多研究学者开始探索信息融合的方法,为小样本可靠性评估提出了一些新的研究思路[1]。
王凤飞等[2]通过融合历史退化数据和失效寿命数据,发现多源信息融合可以提高剩余寿命预测的准确性。贝叶斯方法在信息融合计算方面有着广泛应用,基于贝叶斯理论,贾祥等[3]融合不同的专家经验信息和寿命试验数据来扩充可靠性信息;王博等[4]融合多类型研制试验数据来评估航天阀门的可靠性;Papananias等[5]融合不同来源和制造阶段的数据和信息来提高产品质量。为了提高融合的精准度,有学者考虑在进行数据融合之前,先对信息源给予一个加权处理,比如,王保昌等[6]基于相关函数的多源信息融合方法实现了多个验前分布的融合;文献[7-10]分别采用自适应加权数据融合、利用指数衰减函数度量传感器观测值的相互支持程度、通过定义一致性和可靠性测度进行数据融合权值分配、提出一种基于最优权值的数据加权融合等方法,实现了传感器信息数据的加权融合。张金槐[11]提出了产品验前信息和现场信息进行融合的可信度加权融合方法;Zhang等[12]提出了一种新的加权数据融合方法,该方法可以计算多组先验数据的定量可信度。对先验信息的加权融合有了较深研究后,邵松世等[13]采用似然权重系数对不同来源可靠性信息的可信程度进行了量化,再基于贝叶斯方法实现了多源先验信息的融合及可靠性分析。
以上研究解决了多个先验信息如何进行加权,再与现场信息进行融合的问题,但是其研究仅考虑了不同先验分布的权重,对于多个不同信息源数据信息的变权融合研究甚少。Berger指出先验分布对离群值有较好排除能力的理论[14],以此理论作为准则,在考虑现场真实数据对先验分布权重影响的情况下,实现各个信息源的权重分配,提出一种对多源异构寿命数据信息进行变权融合的贝叶斯可靠性评估模型。
1 权重的确定
多源指试验信息具有多种信息源,异构指这些信息源的数据类型或特征等不一致,在统计学领域认为这类数据不属于同一总体,简称多源异构数据。下面讨论独立异构的寿命信息如何进行加权融合。
假设信息源获取数据的环境条件相同,并将这些数据信息看作是传感器对同一物理量采集到的。记n1,n2,…,nN表示N个信息源分别所对应的样本数,x(i)={xi1,xi2,…,xini},i=1,2,…,N表示第i个信息源下独立同分布的样本;并假设第N个信息源为现场试验信息源获取的真实现场数据。
1.1 各信息源权重的确定
根据各信息源获取的数据信息x(i)={xi1,xi2,…,xini},i=1,2,…,N所反应的总体分布特征,选择适合各信息源的分布类型,拟合得到分布Fi(θ;x),求得各信息源的似然函数Li(x(i)|θ),其似然函数的尾部梯度特征[15]可表示为:
(1)
由现场试验数据x(N)=(xN1,xN2,…,xNnN),求得其似然函数LN(x(N)|θ)的尾部梯度特征为:
(2)
若通过查阅资料等途径获得参数θ的先验分布为φ(θ;u1,u2,…,uk),其中u1,u2,…,uk为先验分布中的超参数,当关于θ的先验信息在其分布的尾部区域取值θ0时,即可得到上述各信息源的尾部梯度特征值τi(Li(x(i)|θ0)),i=1,2,…,N和τN(LN(x(N)|θ0)),比较各信息源和现场试验数据的尾部梯度特征值的绝对值差可得
hi=|τN(LN(x(N)|θ0))-τi(Li(x(i)|θ0))|,
i=1,2,…,N
(3)
当信息源的尾部特征和现场试验数据的尾部特征越靠近时,说明此信息源和现场试验数据越相似,信息源的可信度也越高,所占的权重也应该更高。即各信息源和现场试验数据的尾部梯度特征值的绝对值误差越小,此信息源数据信息所占的权重越大。故各信息源的权重可确定为:
(4)
2 确定各信息源的先验信息
2.1 有先验分布的情形
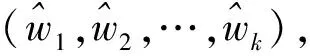
(5)

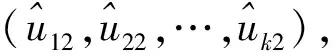
i=1,2,…,N
(6)
2.2 无先验分布的情形
若无关于参数θ的任何先验信息,根据Fisher信息阵的理论知识[16],基于第i个信息源的数据信息x(i)=(xi1,xi2,…,xini),i=1,2,…,N得到其概率分布fi(x;θ),得似然函数为:
计算出参数θ(单参数情形)的Fisher信息阵:
因此,单参数场合下的无信息先验密度函数为:

(7)
3 基于贝叶斯变权融合的可靠性分析
结合前文获取的各信息源权重εi和先验分布φi(θ|x(i)),i=1,2,…,N,以及第N个现场信息源寿命数据关于参数θ的似然函数LN(x(N)|θ),采用贝叶斯估计法[17],考虑对各信息源数据信息估计的先验分布进行加权处理,并且将通过现场试验获得的信息融合到先验信息的估计中,得到一个更客观、合理的先验分布,再以现场试验数据作为样本信息。最终,得到N个信息源数据信息融合后,关于参数θ的联合后验密度为:
φ1,2,…,N(θ|x(1),x(2),…,x(N))=
(8)

(9)

(10)
4 仿真分析

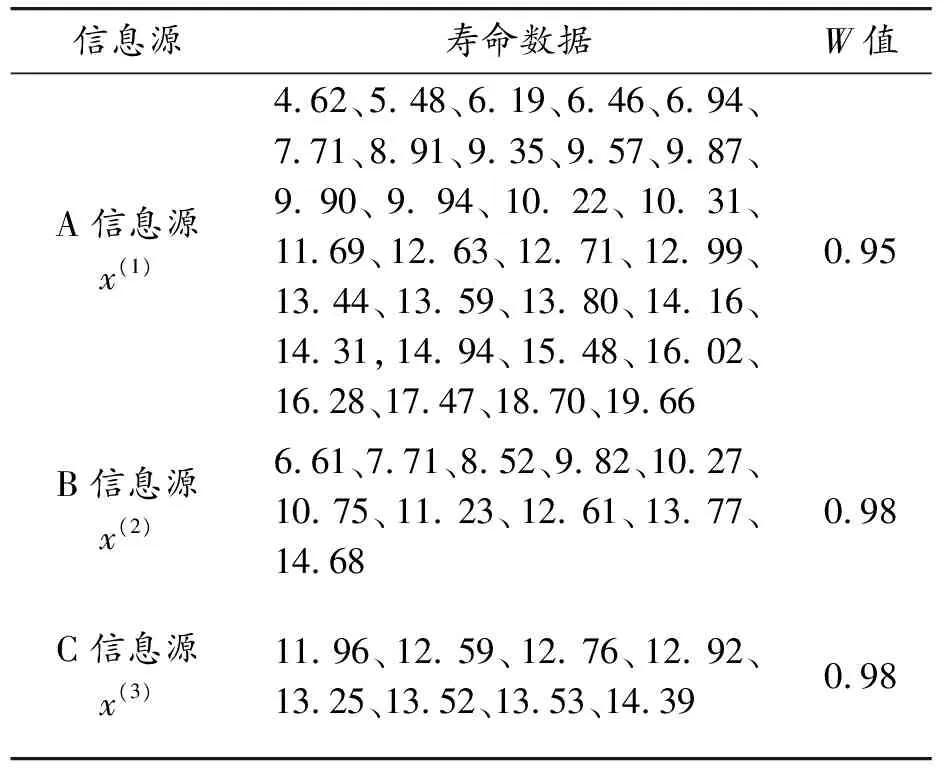
表1 不同信息源数据 年
采用2种变权方式:

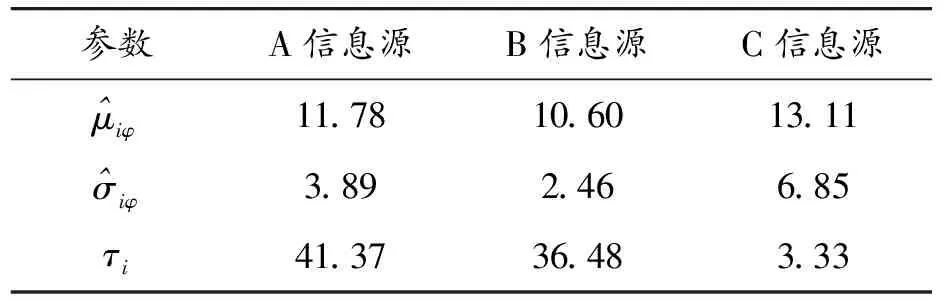
表2 3个信息源先验分布的参数估计结果
根据式(1)和式(2),计算得到A、B、C信息源的尾部梯度特征分别为:
τA=41.37,τB=36.48,τC=τ0=3.33
在参数μ的先验正态分布的尾部3σ域内取值μ0=32.65时,根据式(3)和式(4),获取各信息源的权重占比(见表3)分别为:
εA=0.23,εB=0.27,εC=0.50
根据式(8),可以写出3源样本数据变权融合后,关于平均寿命参数μ的后验密度为:
φA,B,C(μ|x(1),x(2),x(3))=
由式(9),得到在平方损失函数下,产品的平均寿命为:
2) 假设仅对A、B 2个信息源(不考虑现场试验数据对参数μ先验信息的影响)进行加权融合,同理求解,得到A、B信息源的权重占比为:
此时的后验密度为:

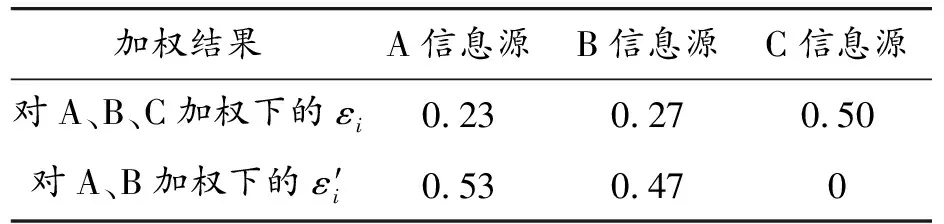
表3 不同加权方式的权重结果
为验证各组寿命数据经过变权实现融合所得到的融合结果,相较于等权融合而言,更具真实有效性,此处使用相同数据,采用贝叶斯理论进行3源等权融合[18],可得到3源等权融合后的后验分布为:

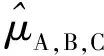

表4 3种不同融合方式获取参数的检验结果
利用表1—4中的数据及参数估计的检验结果可知,通过极大似然法得到A、B、C源的平均寿命分别为11.78、10.60、13.11年,在3源加权、仅对A、B信息源加权和3源等权的3种变权情况下,进行数据融合,获取融合后的平均寿命分别为12.81、12.15、10.87年,说明3源加权融合的评估结果更客观合理,验证了加权融合方法的有效性、合理性。
3源信息均变权进行融合后,得到产品的总体失效密度函数为:
可靠度函数的贝叶斯估计为:
式中:Φ(·)为标准正态分布的分布函数。在3种不同变权融合方式情形下,得到融合前后的可靠度函数曲线,如图1所示。

图1 3源数据在不同加权融合情况下的可靠度函数曲线
通过图1发现3源均变权和仅对A、B变权,2种融合方式得到的可靠度函数结果,介于3源等权融合和C源现场数据融合结果之间,并且3源均变权的结果更靠近C源现场数据的结果,可知变权融合效果优于等权,3源均变权的融合效果优于仅对A、B信息源变权,3源变权融合后的分布总体明显更接近真实现场试验数据的分布总体。因此,将现场试验数据融入先验信息,考虑对各信息源权重占比的影响,使得利用贝叶斯方法做数据融合估计时,先验信息中含有更全面、更客观的参数信息,能更科学合理地评估产品的可靠性。
5 结论
针对小样本数据,提出了基于贝叶斯理论进行多源寿命数据变权融合的可靠性评估模型,获得产品的寿命分布信息及可靠性特性。仿真结果表明,该模型简单易操作,考虑了现场试验数据对参数先验和各信息源权重占比的影响,可以提高评估精准度。从信息论的角度而言,利用各种途径获取的信息数据,避免资源浪费,能够得到对产品更科学合理的可靠性评估分析结论,在统计决策方面也有更好的稳健性,为产品后续的预测研究奠定了基础。
