冲击载荷下频率响应函数的高斯过程回归方法
2023-03-14刘世洲张二亮
任 程,刘世洲,郜 伟,张二亮
(郑州大学 机械与动力工程学院, 郑州 450001)
0 引言
频率响应函数(frequency response function,FRF)是机械系统动态特性评估、振动控制和故障诊断等的有力工具。使用力锤对结构施加冲击载荷,是测量频响函数的重要方式,具有操作简单、成本低和效率高等优点,在机械、土木和航空航天等工程领域得到了广泛应用[1]。因此,开展冲击载荷下频响函数的高精度辨识方法研究具有鲜明的工程应用背景和价值。
基于力锤冲击的FRF测量及其应用已经在诸多学术专著中予以详细介绍。影响冲击载荷下FRF测量的关键因素包括力锤冲击头材质选取、实验方案设计(例如预触发确定)以及信号采集等[2]。Bediz等[3]设计了一种用于微型结构模态实验的冲击激励系统,具有可重复、高带宽和冲击力可控等优点。Xia等[4]开展了玻璃钢拉索的冲击振动实验,采用半功率点法计算实验模态阻尼。针对大型结构的动态特性测量,Tian等[5]提出了基于非接触视觉测量的移动冲击测试方法,以识别整个结构的模态振型和柔度矩阵。
谱估计方法直接从测量的输入输出数据中计算FRF,是锤击法测试中开展FRF估计的主要方法。从算法角度考虑,窗函数设计是影响FRF谱估计精度的主要因素。基于谱估计方法的计算过程,Yang等[6]建立了插值和瞬态误差的非参数模型,分析了窗函数对两种误差的影响。针对谱估计窗函数带来的插值和瞬态误差,Shao等[7]提出了一种迭代补偿方法,用于提高冲击载荷下频响函数的辨识精度。然而,谱估计方法完全依赖于测量数据,FRF的估计精度极易受到测量数据长度和质量的影响。
高斯过程回归(gaussian process regression,GPR)使用无限维多变量高斯分布对函数进行直接建模,已经发展成为一种根据经验样本学习映射关系的非参数高效数据驱动建模方法[8]。相对于经典的谱估计方法,GPR不仅利用了样本数据,还能融合函数模型的固有性质;相比于传统的参数化建模方法,GPR在模型选择方面具有更多灵活性,能够更好地适应数据的变化。高斯过程的性质与其协方差函数(即核函数)有着密切联系。通过刻画系统脉冲响应函数的固有性质(例如光滑、稳定),基于最大熵原理,稳定样条、对角相关等核函数被相继提出和发展,在系统与控制领域内发展了传递函数的正则化估计方法[9-12]。
本文将系统和控制领域的正则化方法引入实验模态分析领域,较为系统地给出了冲击载荷下FRF估计的GPR理论与方法。针对机械系统阶次高及低阶阻尼小的特点,丰富了FRF的复高斯过程先验模型。基于贝叶斯推断框架,利用GPR模型给出了FRF的最大后验估计及其方差,并借助QR分解改善了复高斯过程超参数优化的数值正定性。最后,通过开展平板冲击仿真和叶片振动实验,验证了本文方法的有效性和可靠性。
1 问题描述
在实际的工程测试中,采集的信号都是时域的离散信号,采用离散傅里叶变换(discrete fourier transform,DFT)将时域信号x[t],t=0,1,…,N-1变换到频域X(k),
(1)
式中:k=0,1,…,N/2, j2=-1。
对于线性时不变动态系统,冲击激励u[t]和系统响应y[t]的DFT频谱关系如图1所示,可表示为
Y(k)=G(ωk)U(k)+V(k)
(2)
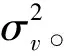
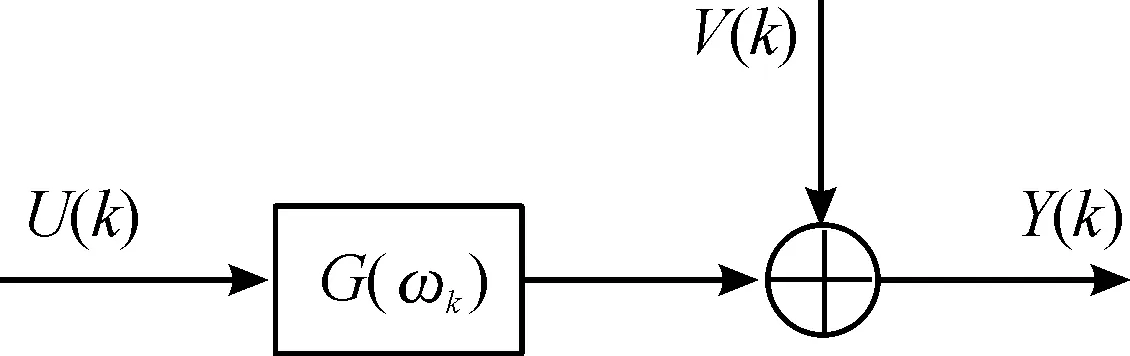
图1 DFT频谱关系
当响应信号采集不完整时,在关系中需要引入额外的瞬态项,用于描述非周期信号傅里叶变换带来的泄露误差[13]。若激励信号具备粗糙性质,该瞬态项可以通过连同FRF一起辨识的方式来剔除。然而,冲击激励的频谱是光滑的,无法分离瞬态项和FRF,则需要通过施加指数衰减窗函数来抑制泄露误差。因而,冲击载荷下的数据采集样本长度应尽可能足够长。
从测量数据Z={(U(k),Y(k)),k=1,2,…,F}(直流分量和奈奎斯特频率除外)中,使用GPR模型对FRF进行高精度建模和估计,是本文要解决的问题。
2 非参数辨识方法
2.1 复高斯过程
基于贝叶斯观点,本文将FRF视作频域上的复值随机函数。进一步,假设FRF是频域上的复高斯向量,即G服从多元复高斯分布。
一般来说,机械结构的FRF在所关心的频带内具有模型复杂度较高、低阶阻尼较小得的特点,导致其建模难度大,这要求复高斯过程具备较强的泛化能力。为此,不同于常用的零均值假设[9-12],本文通过引入FRF的先验均值函数,使复高斯过程充分融合系统的先验信息。复高斯向量G可表示为
G=Gp+ΔG
(3)
式中:Gp为FRF的先验均值函数,ΔG服从零均值多元复高斯分布。
先验均值函数Gp可以借助模态参数识别方法得到。例如,采用PolyMAX方法从测量数据Z中确定动态系统的某些极点pr,再将pr应用于FRF的极点-余项模型,确定模态常数Ar和残余项AU、AL,则
(4)
式中,上标*表示复共轭。
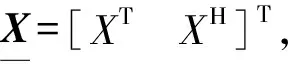
(5)
(6)
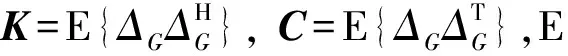
(7)
需要注意的是,核函数K和关系函数C满足K(ωk,ωl)=C(ωk,ω-l)。
高斯过程的核函数刻画了待建模系统的物理信息,在回归分析中起着决定性的作用。对角相关核函数是在系统和控制领域使用最为广泛的核函数之一,描述了脉冲响应的光滑、稳定等基本性质。因此,本文采用对角相关核函数对FRF开展复高斯过程建模,其频域表达式为
(8)
式中:比例因子γ∈R+和核参数α,β∈R+称为超参数。
2.2 似然函数
根据中心极限定理和输出噪声的独立同分布假设,当数据量F→∞时,干扰噪声的DFT频谱是圆形复高斯分布,其关系矩阵为零矩阵。为了与式(5)一致,FRF的似然函数写成如下形式
(9)

2.3 最大后验估计
(10)
式中:∝表示正比于,概率密度函数p(θ)通常假设为均匀分布。
最大后验概率估计常用于参数的推演。联合式(5)(9)和(10),FRF的后验分布仍为复高斯分布,其最大后验概率估计为
(11)
(12)

2.4 超参数优化
超参数θ是未知的,需要从测量数据Z中学习获得,通常采用极大边际似然估计方法。边际似然函数可视作似然函数在先验分布上的期望分布,它能够自动权衡数据拟合精度与模型复杂程度。超参数θ的极大似然估计为
(13)


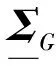
(14)
式中:L是下三角矩阵。根据Woodbury矩阵求逆公式和Sylvester行列式定理可得
(16)
受到式(15)(16)启发,构造如下矩阵,并将其改写成QR分解式,
(17)
式中:Q为正交矩阵,R1为2F维上三角方阵,R2为2F维列向量,r为标量。基于式(17)可以得到
(18)
(19)
(20)
最后,目标函数J(θ)可以化简为
(21)
采用基于梯度的优化算法对目标函数进行最小化,目标函数J(θ)关于超参数θ的偏导数为
(22)
(23)
(24)
式中,Tr表示矩阵求迹运算。
基于式(21)和(22),使用Matlab的优化工具箱中fmincon函数进行寻优计算,便可获得最优的超参数估计。该求解器可用于求解约束非线性多元函数最小值,包含内点优化、SQP优化和信赖域反射优化等不同类型的算法。
最后,根据超参数的最优估计值,结合式(11)和(12)即可获得FRF的估计及其方差,完整的算法流程如图2所示。
3 算例与实验
3.1 数值算例
为了验证本文方法的有效性和可靠性,开展冲击载荷下简支平板的FRF估计。平板的弹性模量为200 GPa,尺寸为1 m×1 m×0.002 m,密度为7 850 kg/m3,泊松比为0.3。在中心位置施加冲击载荷,采用模态叠加法生成系统响应(本算例以速度作为响应),添加高斯白噪声来模拟测量数据,如图3所示。使用的采样频率为1 024 Hz,感兴趣的频带取1~300 Hz,数据样本量F=300。

图2 冲击载荷下FRF的GPR方法流程框图

图3 平板1/4有限元模型 (a)和无噪声响应波形(b)
为了提高仿真运算结果的可靠度,以及对仿真得到的结果进行评价,可进行多次的蒙特卡洛模拟。基于蒙特卡洛模拟,计算均方误差(mean-square error,MSE)对FRF的估计结果进行评价,
(25)
为了显示更宽的数值范围,本文使用分贝(dB)作为FRF幅值和MSE的单位。dB是振动、声学和电信等研究领域常用的无量纲量,可定义为2个数值(测量值X和参考值X0)的对数比率,
1 dB=20lg|X/X0|
(26)
式中,默认参考值X0=1。
考虑响应信号的信噪比(signal-to-noise ratio,SNR)为10 dB的情形,分别使用谱估计方法和本文方法对平板的FRF进行估计,结果如图4所示。与谱估计方法相比,由于借助复高斯过程对FRF的固有性质(光滑、稳定)进行刻画和融合,本文方法可以获得更小的MSE值,FRF的估计精度更高,证明了其有效性。

图4 平板的FRF估计曲线
令式(25)在所有关心频率上取平均,进一步考虑不同SNR情形,MSE均值的计算结果如图5所示。相比于谱估计方法,本文方法在不同的噪声水平下均能够获得更高精度的FRF估计结果,且在低SNR(例如-10 dB)的严苛环境下效果更为显著,证明了其可靠性。

图5 不同SNR下的MSE均值
3.2 振动实验
以长约44 cm的无人机螺旋桨叶片为例,开展锤击振动实验,验证本文方法的实际应用效果。使用PCB 086C03模态力锤激振叶片,利用数字图像相关VIC-3D高速摄像系统测量叶片的振动响应,如图6所示。高速摄像机型号为Photron FastCam Mini UX100,配备了Nikon 60 mm f/2.8 D广角镜头,板载内存容量为8 GB,分辨率为1 024像素×576像素,曝光时间为0.25 ms,并以2 000 fps的帧率进行拍照记录。VIC-3D高速摄像系统的位移测量精度约为6 μm,本实验直接采用位移作为系统响应。

图6 叶片振动实验
为了进一步抑制噪声干扰和减少频谱泄露,本实验对时域信号进行加窗处理:冲击信号施加单位增益窗,响应信号施加指数窗。经过加窗处理的时域信号波形如图7所示。

图7 加窗后时域信号波形
选取感兴趣的频带为1~400 Hz,F=400。分别采用谱估计方法和本文方法对螺旋桨叶片的FRF进行估计,结果如图8所示。2种方法估计的FRF基本吻合,但相较于谱估计方法,由于借助先验信息和全局建模的优势,本文方法估计的FRF波动更小,即随机扰动更小。此外,FRF的谱估计在145 Hz附近存在异常凸起,这极可能是高速相机风扇运转产生的噪声峰值[16],本文方法则能获得更加准确的FRF估计。
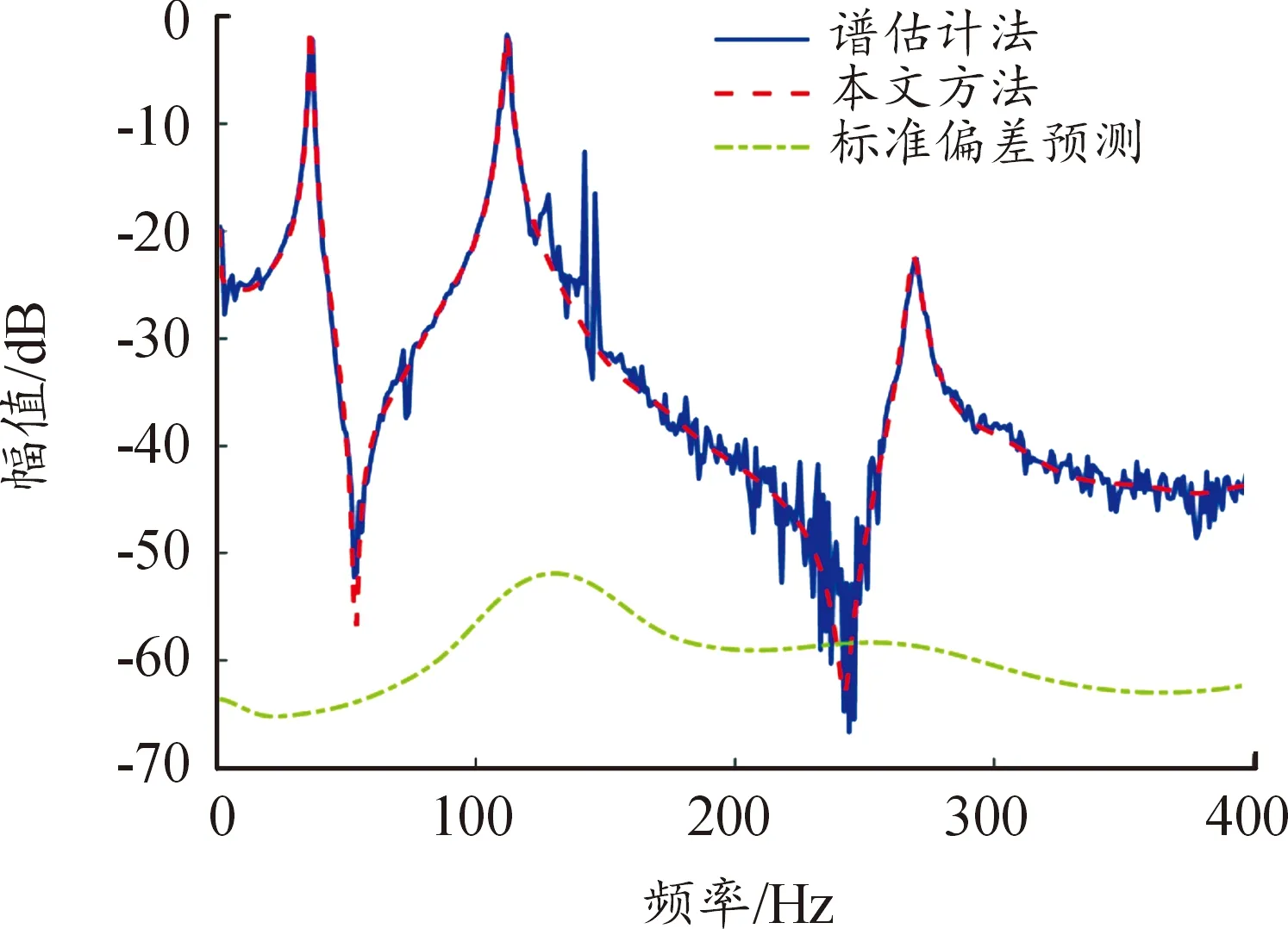
图8 叶片的FRF估计曲线
根据式(12)预测了FRF估计的标准偏差,反映了FRF估计的精度,同时刻画了FRF估计的不确定度在频域的分布情况,在120~150 Hz附近不确定度最大,与该频段存在异常噪声的事实相切合。
4 结论
为了提高冲击载荷下实验模态分析的精度,本文发展了一种基于GPR方法的FRF非参数辨识方法。该方法利用贝叶斯学习技术融合了测试系统的样本信息和模型信息,给出了FRF的最大后验估计及其方差,其有效性和可靠性在平板冲击仿真和叶片振动实验中得到了验证。相比于经典的谱估计方法,本文提出的方法具有更高的FRF估计精度,同时还可给出FRF估计的不确定度描述,为模态测试等领域提供了有力的工具。在下一步工作中,将致力把该方法扩展至有色噪声情形。
