运输规划问题算法的改进
2014-06-12刘雁灵
刘雁灵
(长治医学院 数学教研室,山西 长治 046000)
1 引言
求解运输问题常用的解法是表上作业法,但其本质还是单纯形法[1,2],在确定初始方案时,最常用的方法有三种:西北角法、最小费用法、Vogel法.由最小费用法、Vogel法得出的初始解已比较接近最优解,但仍有不足.大量文献讨论了优化初始方案的算法,文献[3]提出了最大差额法、最大运输量满足法、列差额法,分别从运输角度、最大运输量角度、需求角度出发来建立初始方案,得出的初始方案往往比较接近最优解,有时就是最优解;文献[4]是在Vogel法的基础上提出了最大罚数有两个的情况以及有退化解时提高初始方案的运算法则.本文在前面文献的基础上,给出了新的改进方法,该法往往一步就可以得到最优解,计算量大大减少,并通过实例加以验证.
2 实例与方法
表1运价表(元/吨)
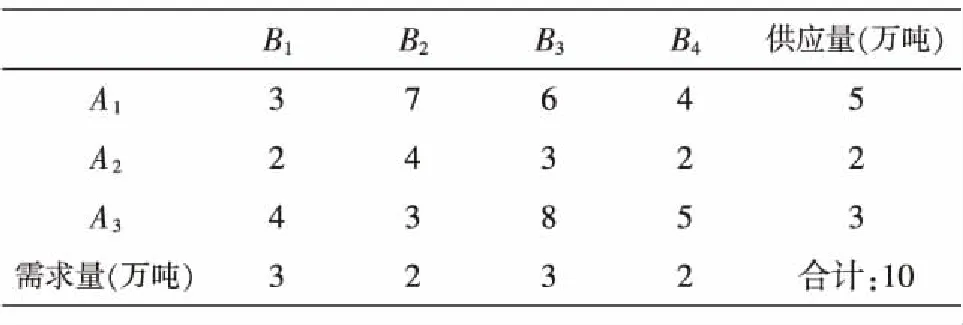
实例1 已知有A1,A2,A3三个产粮地,可供应的粮食分别为5,2,3(万吨),现将粮食运往B1,B2,B3,B4四个地区,其需求量分别为3,2,3,2(万吨).从各个产地运往各个地区的运价如表1[3]所示.试安排一个运费最低的运输计划.
解 具体的计算步骤和相应的差额计算表如下:
步骤:①计算出每一行每一列费用的最大差额,行差额放在表中的最后一列,列差额放在表中的最后一行.如表2中最后一列为4,2,5,最后一行为2,4,5,3;
②在差额最大的数对应的行或列中找费用最小的尽可能满足.这里有两个差额都是5,即第三行和第三列,分别找最小费用,均为3,可任选其一,如先满足差额最大的数5对应的行中的c32=3;x32=2;
③划去已满足需求的行或列,若同时满足可同时划去行和列.表2中划去了第二列;
④重新计算差额,这时注意已经划去的行或列不再参与计算差额,返回到①.
本题中第二次计算出来的行差额为3,1,4,列差额为2,5,3,最大值为5,在5对应的列中找费用最小的尽可能满足,即满足c23=3;x23=2;这时第二行已满足,后面计算差额时不再计算这一行.以此类推,直到供求全部满足,行列全部划去.
表2差额计算表
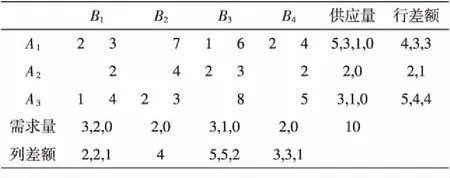
该初始解和文献[3]求得的解一样,已是最优解.
几点注释:(1)当行和列的最大差额有相同的值时,应满足费用最小者,若仍相同,可任选其一;(2)如行列同时满足可同时划去行和列,这时出现退化解,需填“0”,填“0”的方法可参考文献[4]、[6];(3)该法是考虑所有供或求费用的差额最大的情况下满足最小费用的供或求,所以得到的初始解往往就是最优解;(4)所填的数不会超过m+n-1[3].
注:以下实例不再列出运价表,均仿照实例1列出差额计算表进行计算.
实例2 有A1,A2,A3三台机床,加工B1,B2,B3,B4四种零件.已知三台机床的日加工任务量分别为9,5,7(件),四种零件的日需求量分别为3,8,4,6(件),各台机床加工各个零件所需的时间如表3[3]所示.试安排一个总的加工时间最少的生产计划.
解 按照本文方法进行差额计算:
表3差额计算表(小时/件)
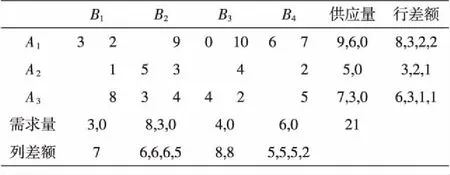
所得初始解为退化解,可按文献[4]或[6]的方法填“0”,如在x13处填“0”,则该解为最优解[3].在文献[3]中计算该题是利用列差额法,但得出的初始解并非最优解,需通过找出调整量才可得出最优解,而本文方法一步即得最优解.
实例3 设某品牌手机生产厂有A1,A2,A3三个分厂,供应B1,B2,B3,B4四个地区销售.已知三个分厂的日供应量分别为70,80,50(台),四个地区的需求量分别为40,30,70,60(台).从各个产地运往各个地区的运价如表4[4]所示.试安排一个运费最低的运输计划.
解 进行差额计算:
表4差额计算表(元/台)
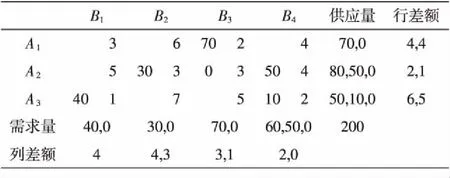
所得初始解为退化解,可按文献[4]或[6]的方法填“0”,如在X23处填“0”,求得的初始解和文献[4]中用Vogel法求得的一致,为最优解.若用西北角法建立初始解则需迭代两次才能得出最优解[4].
实例4 设有A1,A2,A3三个苹果园,供应B1,B2,B3,B4四个地区销售.已知三个苹果园的日供应量分别为8,6,9(百斤),四个地区的需求量分别为5,7,5,6(百斤).从各个苹果园运往各个地区的运价如表5[5]所示.试安排一个运费最低的运输计划.
解 进行差额计算:
表5差额计算表(元/十斤)
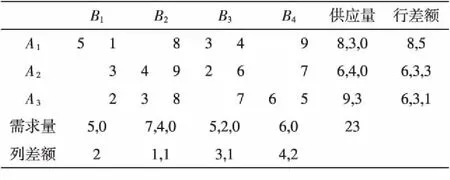
此例得出的初始解和文献[5]通过三次迭代得出的最优解一致.
3 结论
在文献[1-5]的基础上,本文给出了运输问题建立初始方案的新方法:通过寻找行列运费差额的最大值来确定运输方案.通过几个实例的计算,可以看出该法的可行性,而且该法简单易操作,与其它建立初始解的方法相比较,往往一步就能达到最优解,对解决运费差额大的运输问题尤为适用.
参考文献:
[1]宁宣熙.运筹学实用教程[M].北京:科学出版社,2013.
[2]胡运权.运筹学[M].北京:清华大学出版社,1986.
[3]杨莉,等..运输问题的改进算法探讨[J].运筹与管理,2002,11(4):77-80.
[4]郭秀英.论运输问题表上作业法[J].科技与管理,2007,43(3):33-35.
[5]蒋宏峰.运输问题表上作业法的改进[J].长沙大学学报,2002,16(2):47-48.
[6]谢凡荣.产销平衡运输问题的表上作业法解法的一个注记[J].运筹与管理,2005,14(4):44-46.
