一道模拟试题的解法探究及推广

丁胜锋

广东省云浮市邓发纪念中学 (527100)

圆锥曲线综合问题是解析几何的核心内容，是历年高考数学的重要考点之一，也是高考复习备考难突破的难点之一，对于圆锥曲线综合问题，由于题目文字符号多且运算量大，使得学生在解题过程中目标性不强并且方法单一，得分率偏低.在高考复习备考中，我们希望学生能规范答题格式的同时，更能够跳出问题的本身，得到一般性结论和在解题方法上有所突破，避免由于静止地思考问题带来思维的局限性和片面性.本文以一道高三模拟题为例，探求其解法和一般性结论的推广.

图1

本题主要考查直线与椭圆的位置关系和直线过定点问题，体现了直线与椭圆核心内容和圆锥曲线基本思想方法的考查.

一 多视角解析

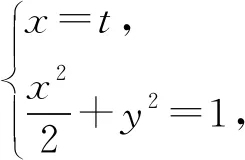
解法1和解法2在思维上很直观，但对运算能力要求较高.解法3思维起点高，运算量少.并且在题设条件发生变化，解法3能减少很大的运算量.

二 性质推广

在问题中1中，点M为椭圆的上顶点，k1+k2=5.实际上，点M可以为椭圆上任一点，k1+k2可为任意常数，可得到以下结论：

图2

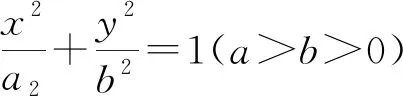
证明：(1)若y0=0，不妨设M为椭圆右顶点，由于k1+k2=0和椭圆的对称性，因此直线AB与y平行，所以AB与y轴同向.

上述讨论是在斜率之和为常数情况下，则直线AB定向或过定点，实际上当两直线的斜率之积为常数时也有类似结论.

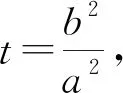
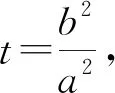
其证明方法与结论1证明方法类似.

以上是以椭圆为载体的斜率之和与斜率之积为常数时，直线定向或过定点，实际上在双曲线和抛物线上也具有类似性质，读者不妨自己证明.