基于数学核心素养发展的余弦定理教学设计*

李 倩 刘成龙 杨坤林

四川省南充高级中学 (637000) 内江师范学院数学与信息科学学院 (641100)

余弦定理是高中数学重要的内容，是解决数学问题的重要工具.具体来讲，余弦定理形式优美，内涵丰富，不仅是勾股定理的推广，同时也是正弦定理的深化，在解三角形中发挥着不可替代的重要.因此，余弦定理引起一线教师们的广泛关注，尤其在如何开展余弦定理的教学上.比如，张跃红基于学生为主体这一理念对余弦定理进行了教学设计[1]，钟进均根据高中学生的心理特点、不同学习水平、不同学习兴趣学生的需要，运用多种教学方法和手段对余弦定理的教学设计进行了深入探究[2]，王思俭基于一堂余弦定理观摩课实录进行探究性教学研究[3]，秦瑾在教育数学思想的指导下，形成一种新颖的相对独立、不依赖旧知识、不需要技巧性的余弦定理教学新方式[4].对已有研究成果进一步分析，可以发现研究者们在教学设计中更多的是关注知识与技能的获取，而对学生数学核心素养的发展关注较少.因此，本文基于发展数学核心素养展开余弦定理的教学设计.

一、基于数学核心素养发展的数学教学

随着《普通高中数学课程标准(2017年版)》的颁布，发展学生数学核心素养正式拉开帷幕[5].数学核心素养是学生在学习过程中形成的能够反映数学思想、数学本质，能够适应自身发展和社会发展需要的、与数学有关的具有综合性、整体性和持久性能力和思维品质.

数学教学不仅是传授数学知识的教学，更是发展数学思维的教学，其最终目的是促进人的发展.数学核心素养和数学教学二者是相互依存，互相促进的关系：数学教学为培养学生的数学核心素养提供载体，学生数学学习中逐步发展核心素养，而数学核心素养既是数学教学的理论基础，也是数学教学的目标指引和归宿.因此，在数学教学中，要以数学核心素养为根据展开顶层设计，为数学教学设计提供方向保障，努力将数学核心素养贯穿于数学教学的每个环节.同时，在教学中将数学核心素养的发展作为基本任务，不断为学生核心素养的发展创造条件.

二、基于数学核心素养发展的余弦定理教学设计

(一)教材分析

本节课内容包含余弦定理的概念、公式、推论以及应用.在此之前，已经学习全等三角形、三角函数、平面几何、平面向量、解析几何、正弦定理等与本节课紧密联系的内容，为余弦定理的发现提供了基础，为余弦定理的多视角证明提供了可能[6].

(二)学情分析

学生已经学习了正弦定理的概念、公式、推论以及应用等基本知识，并能解决简单的三角形问题，具备一定的数学运算能力，数学建模能力、数学抽象能力等.

(三)教学过程

基于核心素养发展，将余弦定理教学设计为五个环节，基本流程是：创设情境——建构模型——合作探究——学以致用——拓展延伸.下文对每个环节进行详细的介绍.

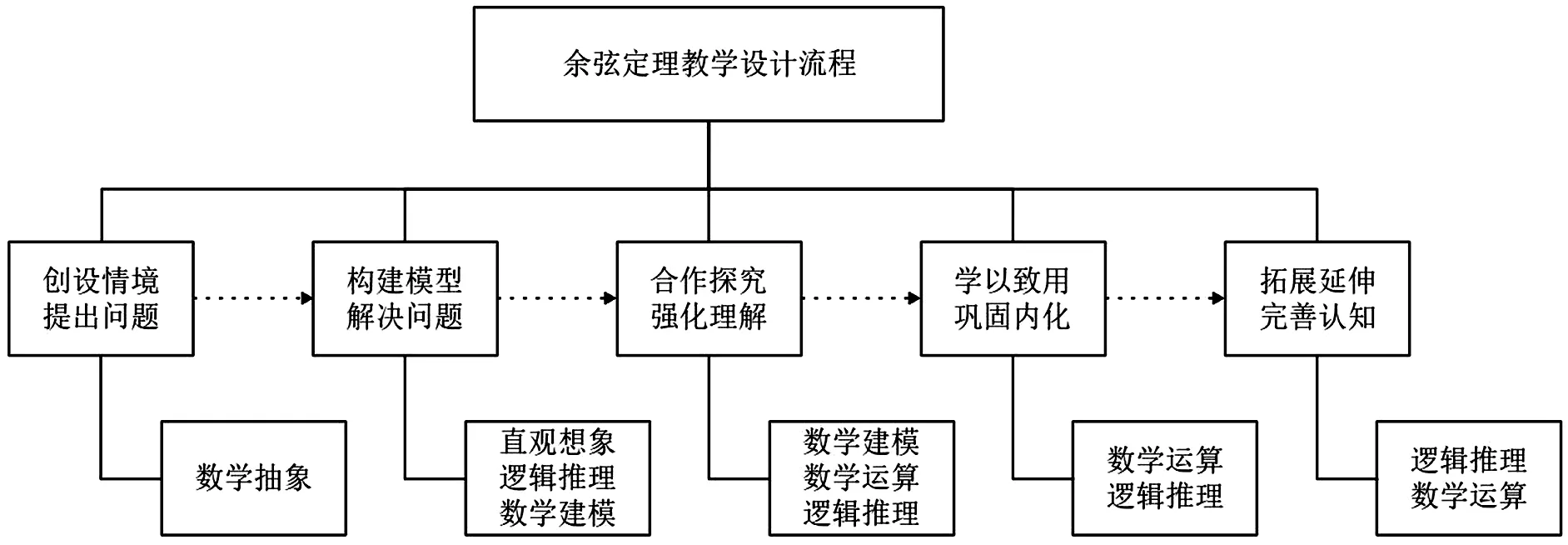
1.创设情境，提出问题

情境1 一列火车从甲地驶往乙地，两地相距800km.但由于途中铁轨故障正在维修，火车需绕行.于是，这列火车在甲地先沿与原方向成60°的方向行驶了600km，再改变方向，沿直线行驶到达乙地.这次行驶路程比原来的800km增加了多少呢？

图1

问题1 能否将上述问题转化为数学问题？

预设：学生对情景水平数学化，得到数学问题(如图1)：在△ABC中，已知AB=600，AC=800，∠A=60°，求BC.

设计意图：让学生体验由现实情境抽象出数学问题的过程，培养数学抽象素养.

2.构建模型，解决问题

问题2 能否将上述数学问题抽象成更一般的数学问题？

预设：在△ABC中，已知b、c和∠A，求a.

设计意图：让学生经历垂直数学化过程，进一步发展学生数学抽象素养.

问题3 你能用正弦定理解答上述问题吗？

预设：用正弦定理解答该问题较难，为进一步学习创设必要，同时引发学生的认知冲突.

问题4 正弦定理的证明方法能否迁移到上述问题的解决吗？

预设：通过作高，将一般三角形转化为直角三角形.在教师引导下，对数学问题进行探究：

(1)如图2，当∠A为锐角时，过B点作AC的垂线，垂足为D.在Rt△ABD中，BD=csinA，AD=ccosA；所以DC=b-ccosA，于是a2=(csinA)2+(b-cosA)2=c2sin2A+b2-2bccosA+c2cos2A=c2+b2-2bccosA.故a2=c2+b2-2bccosA.

图2

图3

(2)如图3，当∠A为直角时，a2=b2+c2，有a2=c2+b2-2bccosA.

图4

(3)如图4，当∠A为钝角时，过B点作CA延长线的垂线，垂足为D.BD=csin(π-∠CAB)=csin∠CAB，AD=

ccos(π-∠CAB)=

-ccos∠CAB，CD=b-ccos∠CAB，所以a2=(b-ccos∠CAB)2+c2sin2∠CAB=b2+c2cos2∠CAB-2bccos∠CAB+c2sin2∠CAB，得a2=c2+b2-2bccosA.综上可知a2=c2+b2-2bccosA.

问题5 能用a、c和∠B表示b吗？能用a、b和∠C表示c吗？

预设：同理可得b2=a2+c2-2accosB，c2=a2+b2-2abcosC.

问题6 通过分类讨论得到了边与角余弦的关系，能用文字语言描述这一关系吗？

预设：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.

教师：上述结论称为余弦定理.

设计意图：在问题解决的过程中，发展学生的直观想象、逻辑推理和数学建模素养.

3.合作探究，强化理解

问题7 还能用其它方法证明余弦定理吗？

预设：学生陷入思考，证明思路不清楚.

问题8 由余弦定理中所包含的两边及其夹角余弦值的乘积你能想到什么？

预设：向量数量积中含有两线段及其夹角余弦值的乘积.

问题9 能否从向量的视角证明余弦定理呢？

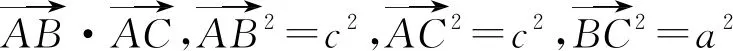
教师：由余弦定理可以得到它的推论：

设计意图：在把握定理的结构基础上，培养学生原型认知能力，在问题解决中，发展学生数学建模、数学运算和逻辑推理素养[7].

4.学以致用，巩固内化

例1 (情境问题)在△ABC中，已知AB=600，AC=800，∠A=60°，求BC.

例2 在△ABC中，b=20cm，c=30cm，C=60°求a.

预设：先用正弦定理求出角B，再运用余弦定理a2=c2+b2-2bccosA解得a.

设计意图：在问题解决中加深公式理解，发展培养学生数学运算和逻辑推理素养[8].

5.拓展延伸，完善认知

问题10 正弦定理和余弦定理有什么关系呢？

任务1：由正弦定理推导余弦定理：

在△ABC中，可知sinA=sin(B+C)=sinBcosC+cosBsinC，由正弦定理得a=bcosC+ccosB.所以a2=(bcosC+ccosB)2=b2cos2C+c2cos2B+2bccosCcosB=b2+c2-b2sin2C-c2sin2B+2bccosCcosB=b2+c2+2bccosCcosB-2bcsinBsinC-(bsinC-csinB)2.又bsinC=csinB,所以a2=b2+c2+2bccosCcosB-2bcsinBsinC=b2+c2+2bccos(B+C)=b2+c2-2bccosA.同理可证b2=a2+c2-2bccosA,c2=a2+b2-2abcosC.

任务2：由余弦定理推导正弦定理：

教师：正弦定理和余弦定理可以相互推导，因此他们是等价关系.

设计意图：学生在完成任务1、2的过程中发展逻辑推理和数学运算素养.

三、教学反思

基于数学核心素养发展的余弦定理教学设计中，教师引导学生通过水平数学化得到数学问题，经历垂直数学化得到更一般的数学模型.在建模、求模、用模、创模(正余弦定理等价)的过程中，以问题为载体，问题解决为线索，让学生始终处于教学活动的中心，把学生数学核心素养的发展作为根本性任务.以数学核心素养为理论指导的余弦定理教学设计为学生核心素养发展提供了保障，同时余弦定理教学设计为数学核心素养发展也提供了载体.