明思想之道,优解题之术
——基于数学思想的2022年新高考全国Ⅰ卷部分试题的求解
2023-03-11王少光
何 灯 王少光
福建省福清东张中学 (350305) 福建省福清第三中学 (350315)
“取势、明道、优术”是中国古代的哲学思想,就是指“明确方向,把握规律,办事有方”.它阐明了做任何事情都应遵循的基本道理,是中华优秀传统文化中的瑰宝,可以成为我们在深化教育领域综合改革的新形势下做好数学教育的指导思想[1].
知识是载体,方法是手段,思想是灵魂,它们是知识体系的三个层次[2].在日常教学中,教师往往注重知识的讲解,方法的传授,却将数学思想的渗透丢弃一旁.为什么很多学生数学的学习仅仅停留在最初级的模仿阶段?题目变一下,就不会了呢?究其原因,绝大多数学生是不懂得站在思想的高度来思考和引领方法,或者是思维混乱导致想不起来用什么方法来求解问题.显然,在教学中渗透数学思想方法尤为重要.
本文以2022年新高考全国Ⅰ卷部分试题为例,就数学基本思想方法的解题策略作一探析,以飨读者.
1.分类与整合思想——分类策略
分类策略是“分类与整合思想”在数学解题中的应用,它是指根据所研究对象的性质差异,区分不同的情况予以分析解决.此类问题有利用考查学生对数学基础知识和基本技能的理解,有助于学生理性思维能力的提高.

分析:本题需要考生利用二项式定理将(x+y)8展开,再利用分类策略讨论第一个括号中取某一项时,第二个括号中需要取哪一项,相乘才能出现与x2y6有关的项.
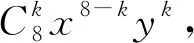
2.函数思想——函数策略
函数策略是“函数思想”在数学解题中的应用,是指在解题中充分考虑对应、相依关系,以及运动变化过程,通过假设变量,构造函数,运用函数概念以及函数性质进行分析与转化,进而达到解决数学问题的策略.在高中数学教学的具体内容中,很多问题的求解离不开函数思想的应用,如比大小、方程根的个数判定、含参不等式问题等.
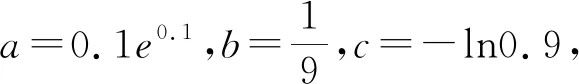
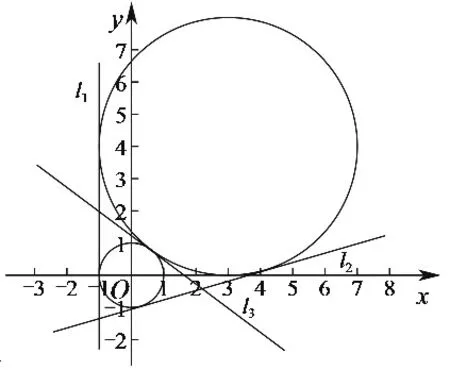
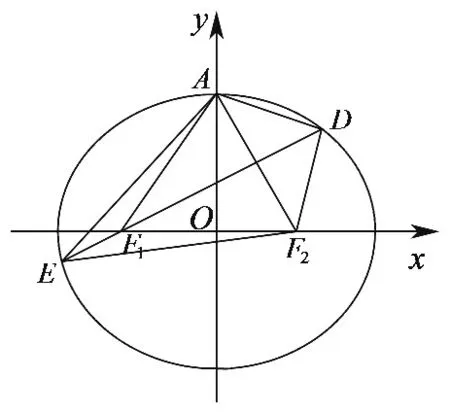
A.a 分析:本题需要考生根据三个数的形式特征,构造适当的函数,利用导数工具进行比较分析. 转化策略是“化归与转化思想”在数学解题中的应用,它是指在研究解决数学问题时,采用某种手段将问题通过变换使之转化,使问题变得熟悉或易于解决的一种策略. 题11 已知O为坐标原点,点A(1,1)在抛物线C:x2=2py(p>0)上,过点B(0,-1)的直线交C于P,Q两点,则( ). A.C的准线为y=-1 B.直线AB与C相切 C.|OP|·|OQ|>|OA|2D.|BP|·|BQ|>|BA|2 分析:本题A、B选项的判定较为容易,C、D选项的判定需要求解出|OP|·|OQ|与|BP|·|BQ|的具体形式,要求考生有一定运算求解能力.若采用转化策略对|OP|·|OQ|与|BP|·|BQ|的表达式进行适当的转化,就可以避免繁杂的计算,将问题轻松解决. 图形策略是“数形结合思想”在数学解题中的应用,它是指利用图象,将数与形之间的对应关系与相互转化来解决问题的策略.“数无形,少直观,形无数,难入微”,利用图形策略有利于分析题中数量之间的关系,丰富表象,引发联想,启迪思维,拓宽思路,迅速找到解决问题的方法,从而提高分析问题和解决问题的能力[3]. 题14 写出与圆x2+y2=1和(x-3)2+(y-4)2=16都相切的一条直线的方程. 图1 分析:本题符合条件的直线有三条,考生只要能够较为准确的画出两个圆,即可通过观察得到直线x=-1符合要求.命题者的考查意图是希望考生在数形结合思想的引领下,画出图形如图1、观察图形、利用图形、求解问题,而不是通过设直线,联立方程等繁杂的方法来求解问题. 图2 分析:本题若分别求出△ADE三边的长,计算量比较庞大,命题者的考查意图是希望考生对题设条件的数量关系作感知,以发掘条件的隐含信息,借助图形,如图2,观察得出图形的关键特征,对所求问题进行转换,以有效解决问题. 特殊化策略是“特殊与一般思想方法”在数学解题中的应用,是指通过选取特殊元素,依据问题在一般情况下真,则在特殊情况下亦真,反之,在特殊情况下不真则在一般情况下亦不真.高考中对它的考查方式主要有:通过寻求特殊值、特殊点、特殊数列、特殊函数、特殊的位置关系等来研究解决不确定问题、运动变化问题、抽象问题等. C.f(-1)=f(4) D.g(-1)=g(2) 日本数学家、教育家米山国藏说过这样一段话:“学生们在学校学到的数学知识,在进入社会后很快就忘掉了,但是,只有深深铭刻于头脑中的数学的精神、数学的思维方法、研究方法、推理方法和着眼点等,却随时随地发挥作用,使他们受益终生.”教师在教学中要充分发掘教材中的知识点和典型例子中所蕴含的数学思想和方法,依靠数学思想指导数学思维、数学问题求解,让学生在潜移默化中去领悟、运用并逐步内化为思维品质,促进学生能力的提升.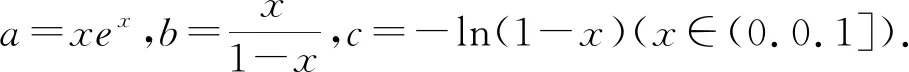
3.化归与转化思想——转化策略

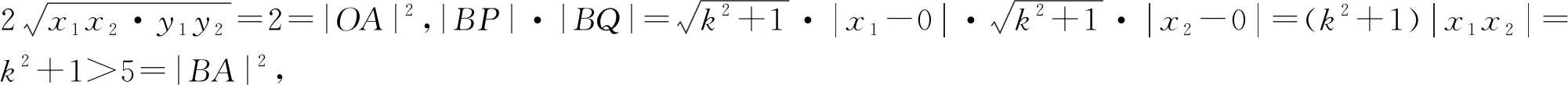
4.数形结合思想——图形策略

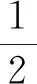
5.特殊与一般思想——特殊化策略


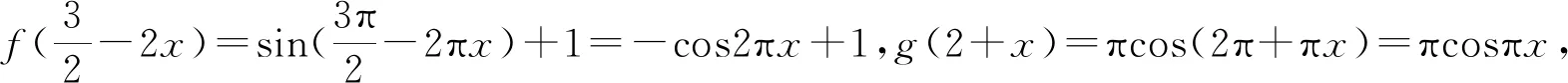
6.结语
