调频连续波激光引信精确定距幅度平方相干算法

刘海明，贺 伟

(西安邮电大学通信与信息工程学院，陕西 西安 710100)

0 引言

由于激光具有高亮度、单色性、发散角小、相干性好等特性，可以建立具有良好时间、空间分辨率和高测距精度的探测系统。激光引信具有波束窄、旁瓣小、抗干扰能力强、精准起爆等优点[1]。现阶段脉冲激光引信以其抗电磁干扰能力强、结构简单、成本低等优点被广泛应用。然而，脉冲激光引信容易受到云雾和烟尘等悬浮粒子物的干扰，难以准确识别目标信号。与脉冲激光相比，调频连续波(frequency modulated continuous wave, FMCW)激光引信是依赖于发射信号和接收信号之间的差频信号，通过频域信号处理方法获取目标距离信息，受回波信号的时域特征影响较小，所以它在相同干扰条件下目标识别能力强于脉冲激光引信[2]。因此，研究在云雾环境中FMCW激光引信对提升引信抗干扰能力具有十分重要的意义。

国内外学者针对云雾对激光引信干扰的问题已开展了大量的研究。文献[3]研究了气溶胶粒径分布对不同波长激光回波信号的影响。文献[4]研究了不同雾霾浓度下散射介质的消光系数对激光后向散射的影响。文献[5]基于单气溶胶粒子后向散射模型，对云雾环境下的目标回波信号展宽现象进行了研究。文献[6]通过仿真相干激光引信在多种云雾干扰场景下的回波信号，分析了回波信号的时域和频域特性。文献[7—8]提出了FMCW激光引信的原型。文献[9—10]研究了FMCW激光引信的烟雾后向散射干扰信号特性并提出了基于频谱幅值归一化阈值的检测方法。文献[11]研究了FMCW激光引信的云雾回波的频域特性，并用样机进行了初步试验研究。文献[12]基于CPSD算法设计了四象限FMCW激光引信，有效地提升了引信的抗干扰能力，然而其复杂和昂贵的缺点限制了它的广泛应用。

本文提出一种新的基于固定距离的幅度平方相干(magnitude-square coherence,MSC)算法，在不增加额外探测器的情况下，依然具有良好的探测精度。

1 云雾中激光散射的原理

大气环境中，在相对湿度和风速等自然条件下，空气中的水蒸气会凝结为水滴悬浮在空中，使得能见度下降。通常云雾的粒径在1～30 μm之间，粒径分布n(r)由对数正态分布描述[13]，定义为

(1)

激光在云雾中传播发生光散射，可以看作是激光束与云雾粒子之间发生碰撞并改变其传播方向。光散射模型主要由米氏散射和瑞利散射来描述。根据粒子大小参数χ：

(2)

式(2)中，λ为激光波长；当χ>1时，光散射主要是米氏散射；当χ≪1时，光散射主要是瑞利散射。激光波长与云雾粒径接近，所以这种情况下选用米氏散射模型更合适，瑞利散射可以忽略不计。

当激光束照射在单个粒子上时，如式(3)所示，激光能量沿散射角的分布情况由米氏相函数描述[14]。

(3)

式(3)中，S1(θ)和S2(θ)分别为平行散射振幅函数和垂直散射振幅函数，an和bn为米氏散射系数。式(3)中的相位函数P(θ)描述了散射角θ中的光的能量。当粒子复折射率m=1.333-0.006i，粒径参数χ=15时，散射角θ和激光能量分布P(θ)之间的关系如图1所示。

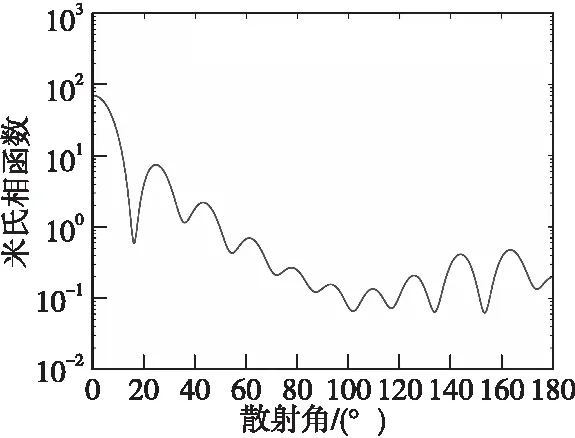
图1 复折射率m=1.333-0.006i和粒子尺寸参数χ=15时的米氏相函数Fig.1 Mie phase function for complex refractive indexm=1.333-0.006i and particle size parameter χ=15

光子在云雾中传播，随着散射次数的增加，光子的能量会逐次减少，当光子能量减少到一定程度，可视为光子被云雾粒子吸收。图2显示了粒子尺寸参数χ分别为10，15和20的情况下，光子后向散射能量强度与散射次数之间的关系。当χ=15时，第1～5次的能量强度占总能量强度的93%，随着散射次数的增加光子后向散射能量强度逐渐降低。

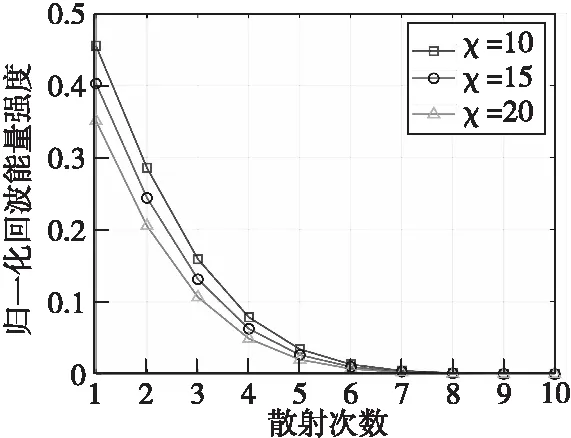
图2 光子散射次数与后向散射强度的关系图Fig.2 The relationship between the number of photon scattering and scattering intensity

2 FMCW激光引信探测模型

FMCW激光引信测距的原理是，引信通过发射镜头发射具有一定线性调制的激光信号，并将一部分激光信号作为本地振荡信号，再对从激光接收镜头接收到的回波信号与本地振荡器信号进行混频，经过低通滤波器，获得频率单一的差频信号。差频信号的频率与目标距离呈线性关系，目标的距离信息可以从差频信号的频率信息中得到。FMCW系统结构图如图3所示。

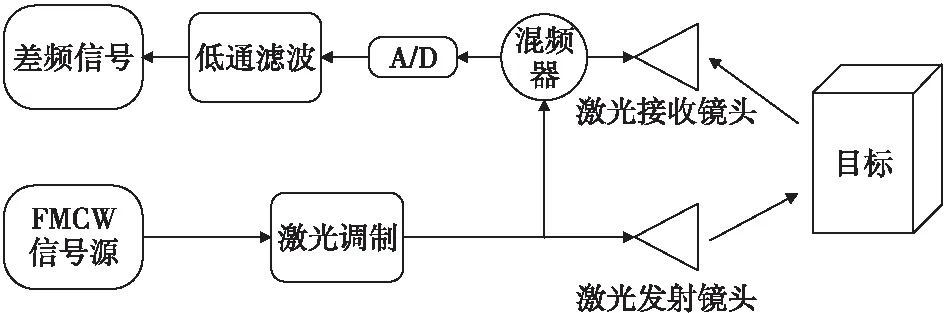
图3 FMCW系统结构图Fig.3 FMCW system structure diagram

FMCW常用的线性频率调制方式有锯齿波调制和三角波调制。锯齿波调制实现目标的测距和测速，需要对差频信号进行二维FFT运算，计算量较大。但是三角波调制相比锯齿波调制在一个周期内做一维FFT运算就可以确定目标距离和速度，处理简单，易于实现,所以被广泛应用。对称三角波的调制模型如图4所示。

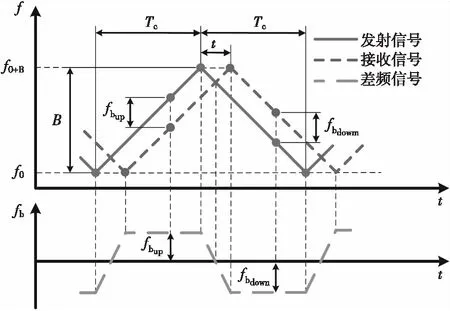
图4 对称三角波调制模型Fig.4 Symmetric triangular wave modulation model

对称三角波调制上下扫频段差频信号的表达式分别为

(4)

(5)

式中，Sbup(t)为上扫频段的差频信号，Sbdown(t)为下扫频段的差频信号；t为某一时刻；A为信号幅度；f0为线性调频的起始频率；f0+B为线性调频的最高频率；τ(t)为延迟时间；μ为调制斜率，μ=B/Tc，B为调频带宽，Tc为调频周期。

当目标静止时，回波信号可以被认为是发射信号的延时副本。为了简化模型，只进行上扫频周期分析，上扫频周期为Tc，差频信号满足fb=fbup=fbdown，因此目标距离R的表达式(6)可写为

(6)

式(6)中，R为引信与目标之间的距离，c为光速。

3 激光在云雾中传输的蒙特卡洛模型

现如今基于Mie散射理论对于单个粒子的激光散射已有大量的研究，然而激光束在云雾中传输过程中，往往是经过多个粒子散射后到达引信的接收镜头，所以必须考虑多次散射。本文基于米氏散射理论，建立了激光在云雾中传输的蒙特卡洛模型。蒙特卡洛方法是将激光束在云雾的传播过程转化为大量独立的光子与云雾粒子发生碰撞的概率模型。激光在云雾中多重散射过程示意图如图5所示。

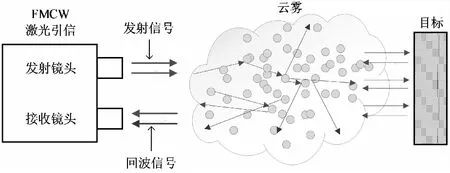
图5 激光在云雾中多重散射示意图Fig.5 Schematic diagram of multiple scattering of laser in clouds

3.1 激光发射模型

FMCW激光引信利用线性调频电信号来调制传输激光信号的光强，瞬时发射光强度可以用光子数表示[9]。激光束通过引信发射镜头发射到探测视角，光子的初始发射时刻的位置遵循高斯分布[15]，由式(7)表示。

(7)

式(7)中，ω0为激光束腰半径；ξ1,ξ2是标准正态分布的随机数。光子在发射瞬间的方向[14]可表示为

(8)

式(8)中，θ0为光子初始发射方向的天顶角，φ0是光子初始发射方向的方位角。

3.2 激光传输模型

(9)

当光子与云雾粒子发生碰撞后，方向发生变化，如图6所示，Dm=(ux,m,uy,m,uz,m)为碰撞后新的方向向量，Dm-1=(ux,m-1,uy,m-1,uz,m-1)为碰撞前光子的方向向量。

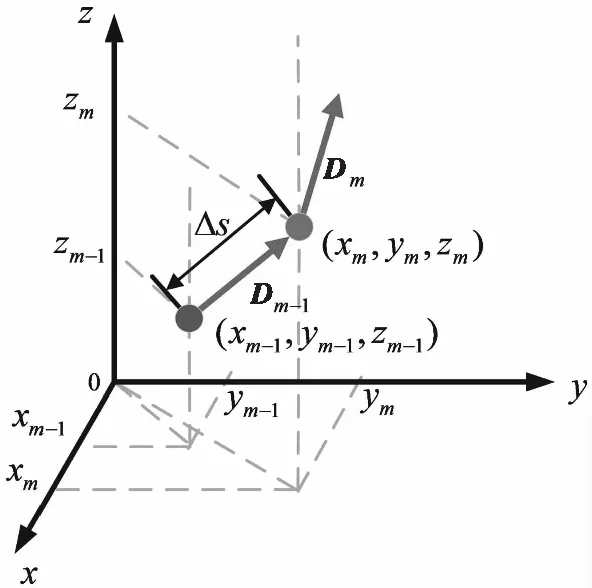
图6 光子散射后运动方向示意图Fig.6 Schematic diagram of the direction of motion after photon scattering

光子与云雾粒子碰撞散射后的移动方向由散射角θm和天顶角φm决定。散射角θm根据式(3)相位函数P(θ)得到，天顶角φm是[0,2π]之间随机角度。那么光子碰撞后的新方向[17]可以表示为

(10)

当|uz,m-1|>0.999 99时，式(10)可以简化为

(11)

当光子在传播过程中与目标碰撞，会被目标反射改变方向和能量，则光子经目标反射后的方向为

(12)

3.3 云雾衰减模型

云雾对激光衰减特性由消光系数γe和散射系数γs来描述。光子与云雾粒子或者目标碰撞后，沿着散射角继续传播。衰减函数ω与云雾消光系数γe和散射系数γs的关系[7]为

(13)

建立权重函数Wn来表示光子每次与云雾粒子碰撞后的状态，每个光子的初始权重W0为1，随着碰撞次数增加，光子的权重会越来越小。权重函数为

问指不耻向别人求教，善于与别人交流。问也是道德培育和养成的又一重要途径和方法。《论语》明确指出：“敏而好学，不耻下问。”“疑思问。”“子曰：‘三人行，必有我师焉；择其善者而从之，其不善者而改之。’”意思是，天资聪敏，勤奋好学，向地位低下的人求教而不怕人耻笑；遇到疑问时，就应该及时去请教别人。孔子说：“三个人在一起走路，其中一定有我的老师。我接受他们正确的意见，抛弃错误的观点。”俗话说“学问”，可见“学”和“问”是无法分开的，“学”是获得学问的重要途径，“问”当然也是获得知识的重要手段。又学又问，才能成为一个有“学问”的人。

(14)

式(14)中，ζ为预先设定的小值。当Wn+1≥ζ时表示光子继续传播；当Wn+1<ζ时Wn+1=0表示光子被云雾粒子吸收。

4 FMCW激光引信精确定距计算

4.1 幅度平方相干算法

MSC算法可以在频域中比较两个信号的相似性。因此，当使用MSC算法进行固定距离时，计算机根据预期距离计算理想条件下的差频信号频率，得到信号波形，即参考差频信号的波形。理想情况下，差频信号是单频余弦信号，其频率与引信和目标之间的距离成线性关系。理想条件下的差频信号称为参考差频信号。根据FMCW激光探测原理，参考差频信号Sbe(t)是具有一定频率fbe的余弦信号。fbe可通过式(15)计算：

(15)

式(15)中，Re为预先设定的距离。

本文利用MSC算法比较参考差频信号和测量差频信号在频域上的相似性，作为引信固定距离的判断依据。如果频谱分布中的fbe处出现频谱峰值，则意味着两个信号都包含该频率，且目标的实际距离与预先设定的距离相等。

在激光引信工程的实施中，测量差频信号Sb(t)和参考差频信号Sbe(t)是离散的数字信号，可以表示为Sb(n)和Sbe(n)，测量差频信号Sb(t)和参考差频信号Sbe(t)信号的功率谱密度分别为

(16)

(17)

式中，rSb,Sb[k]=ε{x*[n]x[n+k]}和rSbe,Sbe[k]=ε{x*[n]x[n+k]}分别为测量差频信号Sb(t)和参考差频信号Sbe(t)的自相关函数。

同时，测量差频信号Sb(t)和参考差频信号Sbe(t)的交叉功率谱密度[18]为

(18)

式(18)中，rSb,Sbe[k]=ε{x*[n]y[n+k]}为测量差频信号Sb(t)和参考差频信号Sbe(t)的互相关函数。

因此它们之间的幅度平方相干性表达式[19]为

(19)

在没有云雾干扰的情况下，测量差频信号Sb(n)中只有目标回波信号Sbt(n)和随机噪声。此时，如果目标与引信之间的距离等于预先设定的距离Re，则参考差频信号的频率与目标信号频率一致，Sbt(n)和Sbe(n)只有振幅和相位差。相应地，在幅度平方相干的频率fbe处出现一个明显的峰值。此时，可以确定与目标的当前距离，以满足固定距离条件。在云雾干扰条件下，目标信息淹没在云雾回波和噪声中难以提取。通过MSC算法，只保留两个信号中的相关部分，这可以大大降低提取目标信息的难度。

4.2 幅度平方相干算法实现FMCW激光引信固定距离目标检测

基于MSC的固定距离算法的基本步骤如下：

1)获取当前测量的差频信号Sb(t)；

2)根据预先设定的距离Re计算频率fbe，并且生成参考差频信号Sbe(t)；

3)通过MSC算法计算Sb(t)和Sbe(t)的幅度平方相干函数C2(f)；

4)在MSC结果中，如果在参考差频频率fbe处出现大于阈值的峰值，证明目标被检测到；如果小于阈值的峰值，则返回步骤1)重新开始检测。

5 仿真与实验

基于FMCW激光引信在云雾中传输的蒙特卡洛模型进行回波信号仿真，仿真流程图如图7所示。

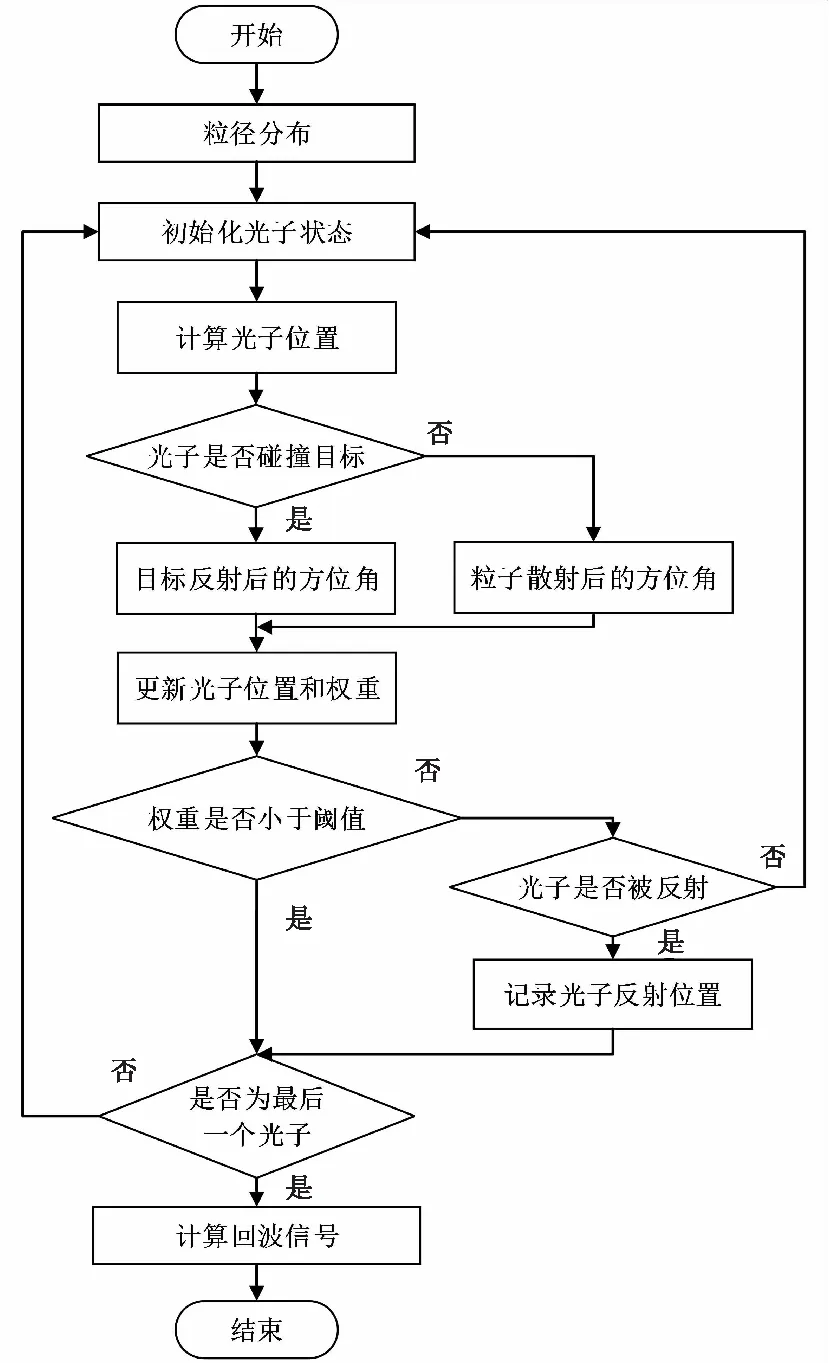
图7 仿真流程图Fig.7 Simulation flow chart

基于MSC算法对“目标无云雾干扰条件”、“目标有云雾干扰条件”和“无目标有云雾干扰条件”三种场景进行了仿真。将MSC算法的处理结果与FFT算法的处理结果进行比较，验证了MSC算法在烟雾干扰条件下的优势。云雾对激光的干扰程度采用空气能见度指标来描述，能见度50、30、10 m分别对应轻度、中度、重度浓度干扰条件[20]。

仿真中的引信参数如表1所示。

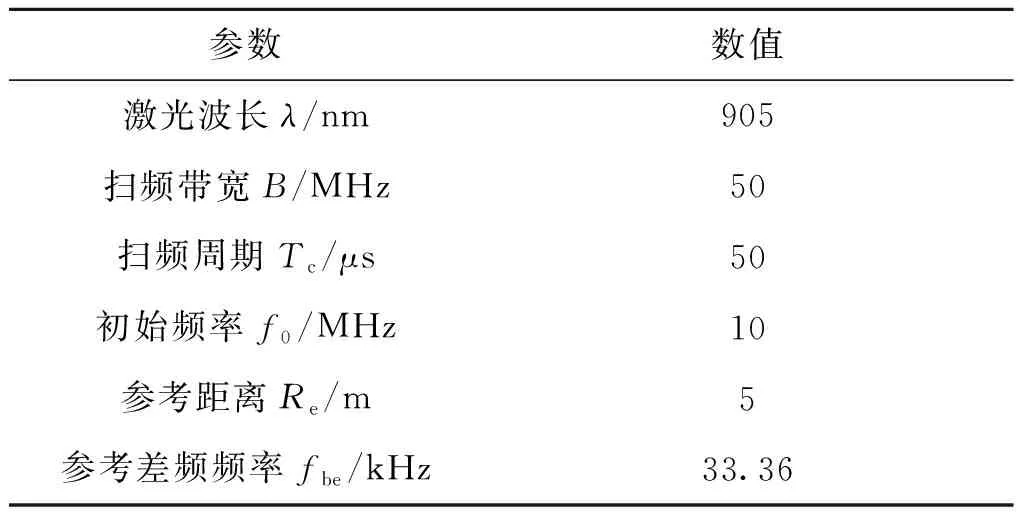
表1 FMCW激光引信仿真参数Tab.1 FMCW laser fuze simulation parameters

5.1 目标无云雾干扰条件仿真

图8显示了无云雾干扰条件下固定距离为5 m的仿真结果。图中实线表示测量差频信号，虚线表示参考差频信号。从图8可以看出，在5 m距离处，MSC算法和FFT算法的处理结果在参考差频处都有明显的峰值，满足引信起爆条件。在9、12 m距离处，两种方法的处理结果在参考差频附近没有峰值，不满足引信起爆条件，满足预先设定的在固定距离处目标识别。

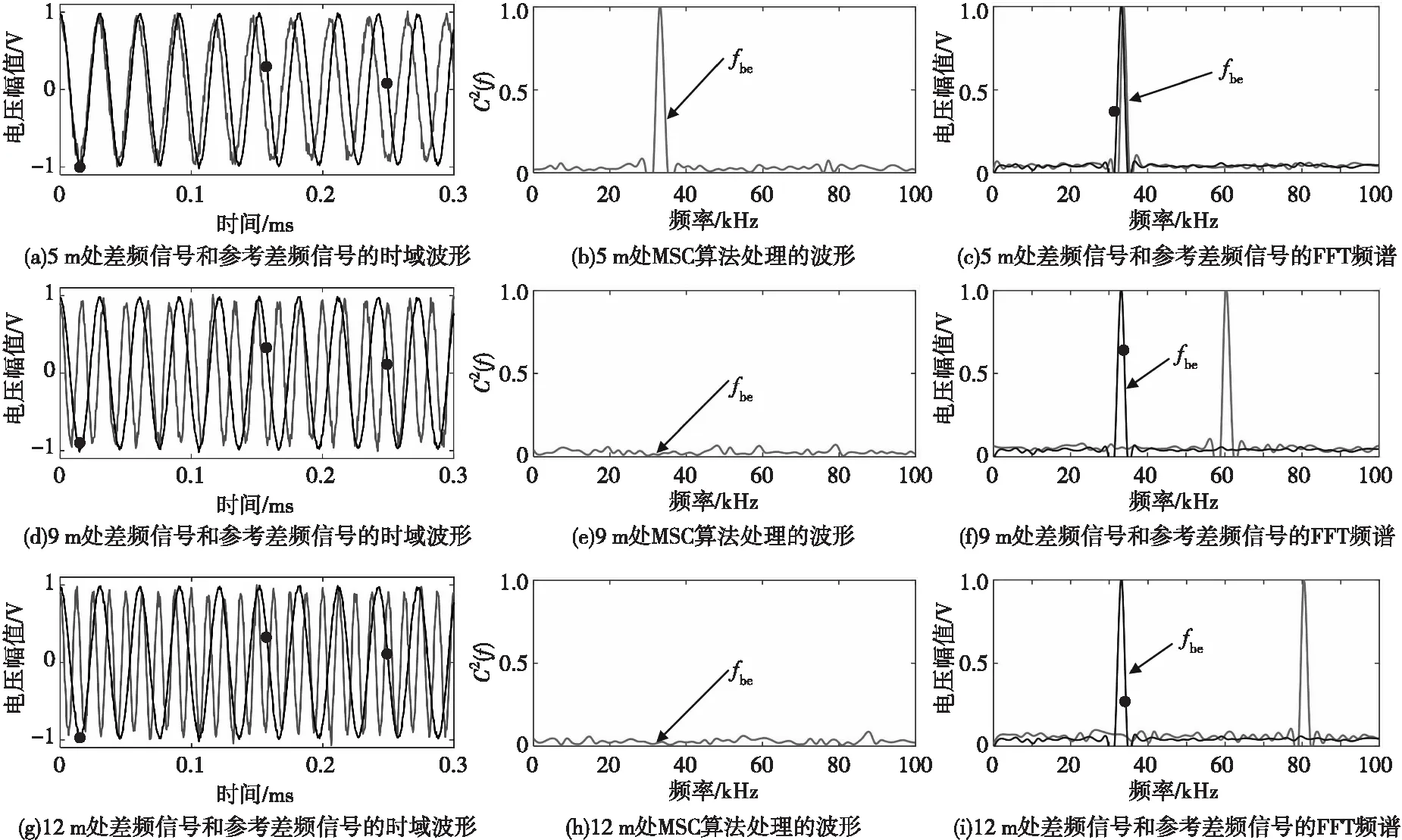
图8 当固定距离为5 m且无云雾干扰时的仿真波形与频谱Fig.8 Simulated waveform and spectrum when the fixed distance is 5 m and there is no cloud interference

5.2 目标有云雾干扰条件仿真

图9—图11为固定距离为5 m时，低浓度(能见度50 m)、中浓度(能见度30 m)和高浓度(能见度10 m)云雾干扰条件下的仿真结果。图中实线表示测量差频信号，虚线表示参考差频信号。从图中可以看出，在低浓度干扰条件下，MSC算法和FFT算法的峰值集中在与目标距离相关的频率处，并未出现干扰峰值; 在中浓度干扰条件下，在与目标距离相关的频率处存在峰值，在其他频率点处也出现峰值，但峰值水平相对较小; 在高浓度干扰条件下，既存在目标峰值，也存在与目标峰值水平相当的干扰峰值。随着云雾浓度的增大，云雾对激光的后向散射强度也越大。FFT算法频谱中干扰峰值水平变高，在高浓度云雾条件下存在与目标峰值强度相近的干扰峰值，会造成引信误判，无法准确识别目标。当目标距离等于固定距离时，MSC算法频谱中参考差频fbe处都有明显的峰值，满足引信起爆条件。当目标距离不等于固定距离时，干扰峰值水平增高幅度较小，峰值水平依然小于0.5，不满足起爆阈值，与预期的效果一致。

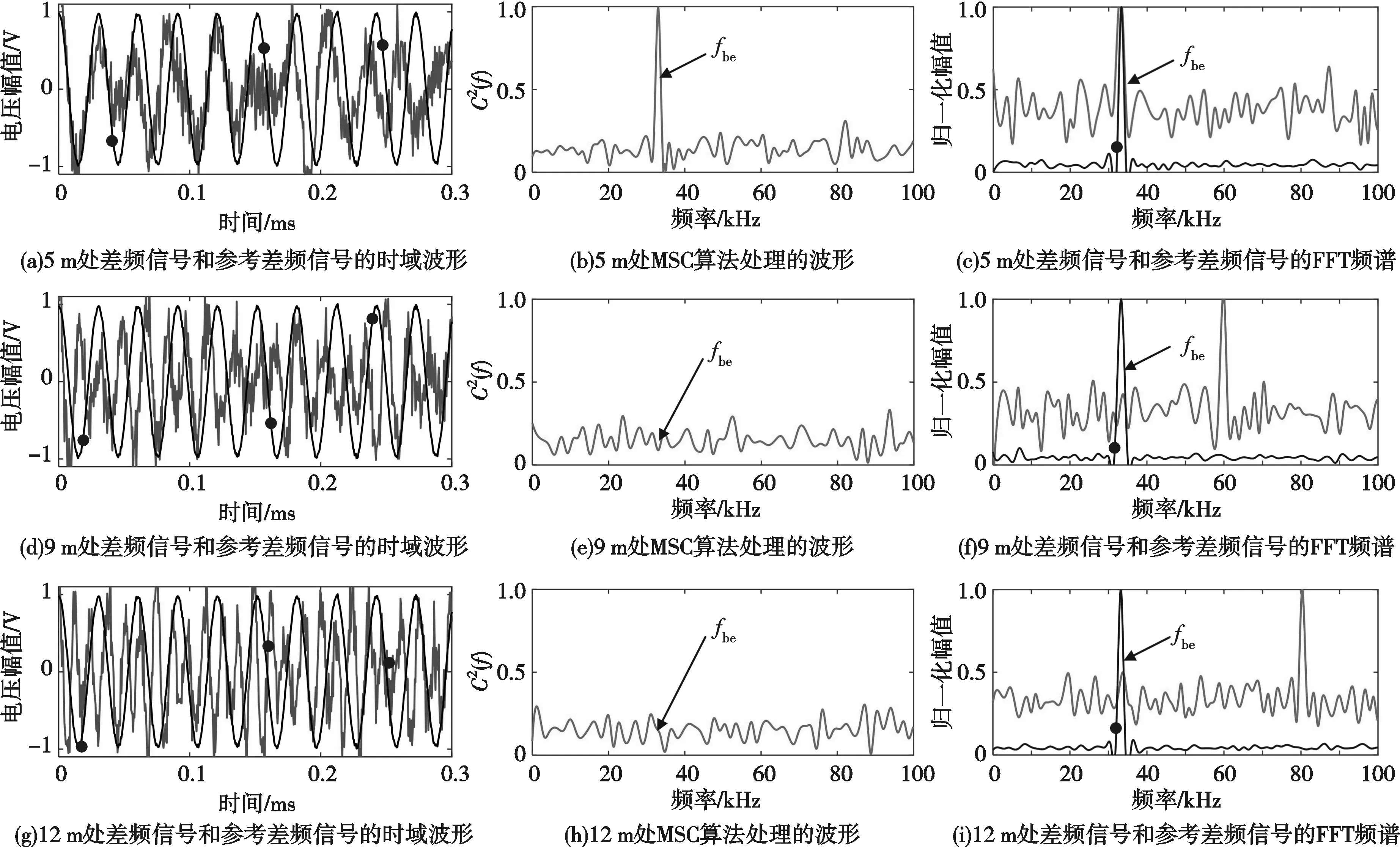
图10 当固定距离为5 m且中浓度云雾干扰时的仿真波形与频谱Fig.10 Simulated waveform and spectrum when the fixed distance is 5 m and medium concentration of cloud interference

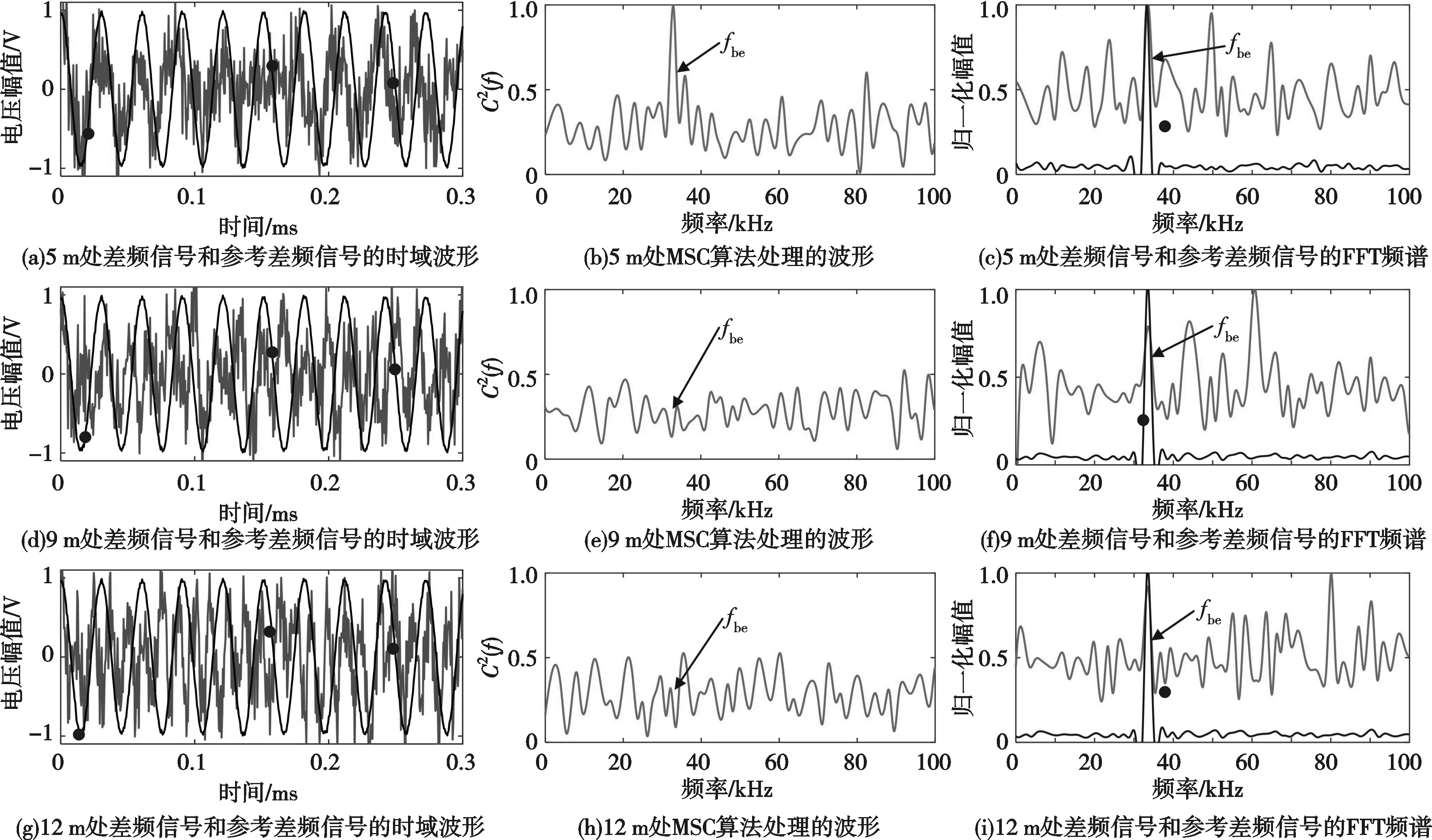
图11 当固定距离为5 m且高浓度云雾干扰时的仿真波形与频谱Fig.11 Simulated waveform and spectrum when the fixed distance is 5 m and high concentration of cloud interference

5.3 无目标有云雾干扰条件仿真

图12为固定距离为5 m时，在中浓度(能见度30 m)云雾干扰条件下无目标的仿真结果。从图12可以看出，在5 m处云雾距离与固定距离相等，MSC算法结果中出现幅值较小的峰值，是由于云雾的后向散射引起的，峰值水平不满足引信的起爆阈值；在9、12 m处，MSC算法结果中无明显峰值，和预期结果一致。

图12 中浓度云雾干扰条件下无目标仿真Fig.12 Simulation of cloud interference conditions without target medium concentration

综上所述，MSC算法可以有效地抑制烟雾干扰。通过参考信号fbe和测量信号fb之间的相似性比较，保留了具有fbe频率的目标信号，与FFT算法相比有较好的目标识别精度。

为了验证所提出的MSC算法相较于传统FFT算法具有良好的抗干扰性能，进行了对比实验，对比两种算法在不同云雾干扰下的识别正确率。通过不同云雾干扰下分别进行10次目标识别实验，结果如表2所示。由表2可看出，在不同云雾干扰下，提出的MSC算法具有较高的目标识别正确率。

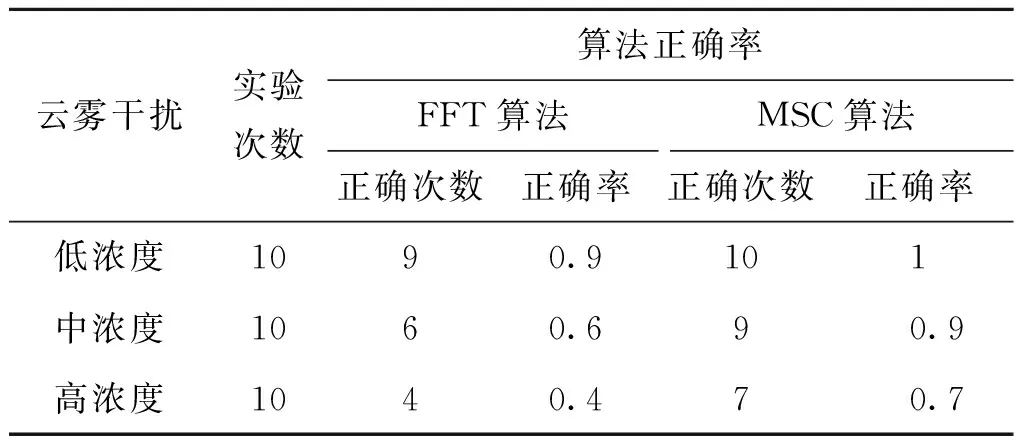
表2 不同云雾干扰下两种算法的识别正确率Tab.2 Correct recognition rate of two algorithms under different cloud interference

6 结论

本文基于FMCW激光引信测距原理和Mie散射理论，采用蒙特卡罗方法建立了FMCW激光在云雾中传输的数学模型。该模型根据光子空间位置和云雾粒径分布实现了光子在云雾中的多次散射和多径传播。通过仿真不同干扰条件下目标回波信号和云雾回波信号的差别，采用固定距离的方法并利用MSC算法对回波数据进行处理。仿真结果表明MSC算法在云雾环境中有良好的抗干扰能力，在低、中和高浓度云雾条件下，目标识别正确率均高于FFT算法，为FMCW激光引信抗云雾干扰提供了参考。