包含无效点滤波的弹道高度预测

徐瑞辰，牛兰杰，2，张 珂，2

(1.西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

近炸引信对现代武器系统的作战效能具有重要作用，而弹道高度的测量精度是影响近炸引信最佳炸点起爆的重要因素。目前典型近炸引信，如无线电引信、光学引信的弹道高度测量精度要求一般小于3 m，美军部分引信炸点控制精度小于1 m，因此提高弹道高度测量精度具有重要实用意义。

近年来，国内外学者开展了在不降低目标检测概率前提下，提升测量数据更新速率、降低弹道环境噪声引起的随机误差，进而提高测距精度的研究。文献[1—7]分别用最小二乘法或矩阵加权等方法，提出了不同形式的融合卡尔曼滤波器，用于降低信号发生丢失时的预测误差。文献[8—10]研究了利用最小二乘法、内插外推算法、三次样条插值、RBF神经网络等改变测量数据更新速率以进行时间对准的方法，但计算复杂度和样本量需求高、抗干扰能力弱，难以在弹载平台使用。文献[11]在研究异步信号融合系统时利用伪测量原理，通过对高数据更新速率的传感器数据进行最小二乘估计，用量测估计值代替量测真值，调整数据更新速率，将异步数据融合转化为同步数据融合，然而此方法仅限用于均速运动模型，适用面窄，不适用于机动性较强的弹药平台。文献[12—13]分别通过建立不同采样时刻下的状态空间模型，利用融合递归的方式进行异步融合。此外，文献[14—17]研究了基于伪测量法或序贯融合法的异步融合技术，可用于改变信息更新速率。

综上所述，改变信号采样间隔、提高探测精度的算法已较为成熟，经典的方法有多点插值法、状态空间分解法、伪测量法和新兴的神经网络算法等，其中异步信号融合系统中常用的卡尔曼滤波算法和伪测量法具有滤波精度高等优点，但是由于引信在对地弹道高度测量时，具有处理速度高、实时性强等特点，传统基于伪测量技术的卡尔曼滤波算法包含大量矩阵求逆运算，难以满足弹上环境对计算量的要求。本文针对弹载使用平台，以减小计算量和实现高度预测为目标，提出无效点概念，将探测漏点、干扰点、需插值点设置为两种类型的无效点，将无效点和额外预测点利用系统状态方程、扩展卡尔曼滤波、伪测量技术等处理算法进行滤波和更新，进行弹道高度预测，达到降低测量误差、降低采样间隔的效果。

1 高度预测算法

1.1 卡尔曼滤波算法

卡尔曼滤波算法在弹药制导、防空雷达航迹预测等场景中得到广泛使用，可以预测运动目标轨迹，特别是在信号受到干扰或者测量精度不够时能够有效避免因信号丢失、测量精度低、受环境噪声干扰等原因导致的测量数据失效问题。

本文采用的卡尔曼滤波算法根据目标之前的运动状态推算下一步运动状态，可以降低测量误差，减少随机噪声影响，并预测后续运动状态，而且仅利用已知历史信息即可进行实时计算，具有计算实时性强等特点。

1.1.1预测与更新流程

卡尔曼滤波(Kalman filter, KF)是最优估计理论之一，用于递推系统状态的最小方差线性无偏估计，能估计下一步状态和下一步误差协方差。

在不考虑控制输入量的情况下，卡尔曼滤波的线性、离散系统方程和测量方程分别如下：

xk=Φk|k-1xk-1+Γk|k-1wk-1,

(1)

zk=Hkxk+vk,

(2)

式中，xk为系统的状态向量，zk为可以实际测量的量(观测向量)，Φk|k-1为状态转移矩阵，Γk|k-1为过程噪声分布矩阵，Hk为观测矩阵，wk-1为过程噪声，vk为测量噪声，二者都是均值为零高斯白噪声，且互不相关。过程噪声协方差为Qk(非负阵)，测量噪声协方差为Rk(正定阵)。

1)状态的一步预测方程为

(3)

2)均方误差的一步预测方程为

(4)

式(4)中，Pk|k为状态估计误差协方差阵。

3)滤波增益权重方程为

(5)

4)滤波估计方程(更新方程)为

(6)

5)误差协方差更新方程为

Pk|k=[In-KkHk]Pk|k-1。

(7)

将步骤5)得到的结果，代回步骤1)，即可完成全状态估计。

在对地近炸引信测高使用场景中，同样可以采用卡尔曼滤波算法对弹道高度进行估计，在存在干扰信号时高度预测效果示意图如图1所示。

图1 高度预测效果示意图Fig.1 Height prediction effect

本文采用卡尔曼滤波算法对高度测量信息在时间-距离维度进行预测，由于卡尔曼滤波算法对非线性航迹适应力不足，且无法完成提高数据更新速率等工作，因此需要做出改进。

1.1.2扩展卡尔曼滤波算法

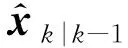
xk≈Φk|k-1xk-1+Γk|k-1wk-1，

(8)

zk≈Hkxk+vk。

(9)

之后即可利用标准卡尔曼滤波方法进行迭代，其中状态转移矩阵Φk,k-1和观测矩阵Hk分别由f(*)和h(*)的雅可比矩阵来替代。

1.2 伪测量法

在近炸引信对地测高过程中往往存在有效量测信息丢失的现象，因此需要通过已确定的量测信息求解在需要量测信息丢失时刻的状态向量，代替真实量测值，此算法称为伪测量法。

(10)

(11)

为了简化公式，设

(12)

(13)

则式(11)可以简化为如下伪测量方程：

(14)

且伪测量的协方差矩阵的完整形式为[16]

(15)

2 包含无效点滤波的弹道高度预测算法

一组实测弹道高度信息如图2所示，此实测信息存在量测数据丢包、信息更新速率不足、受到干扰等问题，因此，需要对经典滤波算法进行改进，以降低上述问题带来的测量误差，提高测量数据更新速率。

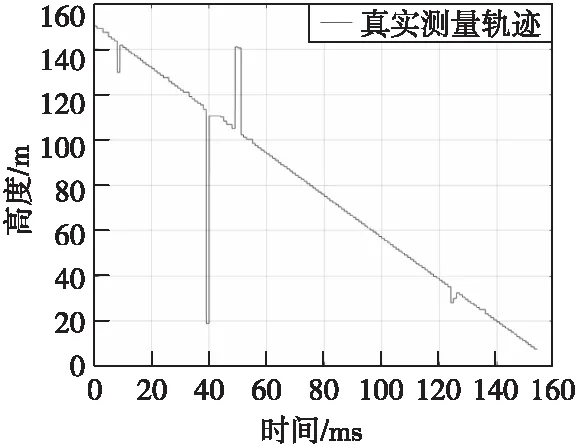
图2 一组实测弹道高度信息Fig.2 A set of measured ballistic altitude information

2.1 无效点预测流程

本文引入无效点概念，利用伪测量方法，在不进行复杂插值计算的前提下对这些问题一次性完成处理。

当检测到以下三种场景时引入无效点概念：1)每次检测到输入的测量值连续不变或出现漏点时，将连续不变的点或漏点设置为A类无效点；2)检测到出现超过预设阈值的极端跳变点时，将超过阈值的点设为A类无效点；3)在每两个采样点间进行插点，如需将测量数据更新速率提高P倍，可在原离散测量值的每两个点之间插入P-1个新点，并将这P-1个新点设为B类无效点。之后，利用系统状态方程、扩展卡尔曼滤波、伪测量算法对无效点进行预测和更新。

对无效点的预测流程如下：

步骤2)对修改后的量测信息进行一次扩展卡尔曼滤波处理。

步骤3)对于B类无效点，为了减少计算量和减少量测误差的影响，对步骤2)中的每个采样点的卡尔曼滤波结果，代入预测方程式(3)进行预测，得到连续的P-1个B类无效点中首个点的预测结果，状态转移矩阵的参数t取T/P；对其余P-2个B类无效点，每一个无效点的结果由前一个无效点通过式(3)进行预测，误差协方差阵由式(7)更新。

步骤4)用步骤3)的预测结果作为高度估计结果，由于原始量测信息的每两个采样点间插入了P-1个预测点，因此测量数据更新速率提高了P倍，理论上P可以取任意正整数值。

2.2 额外点预测流程

实际应用中，当引信持续受到干扰时有效量测信息持续丢失。因此，需要对高度信息进行额外预测。

由于无效点预测流程具有可以预测无数据点的功能，因此也可实现额外点预测，且理论可以额外预测任意点之后的结果，额外预测的点数越多，与实际值偏差越大。

图3为B类无效点预测流程和用同样方法进行额外点预测的流程。图中，P：采样率提高的倍数(如采样间隔由20 ms提高到0.5 ms，则P=40)；N：原始信号序列长度；额外预测点数=M·(P-1)。

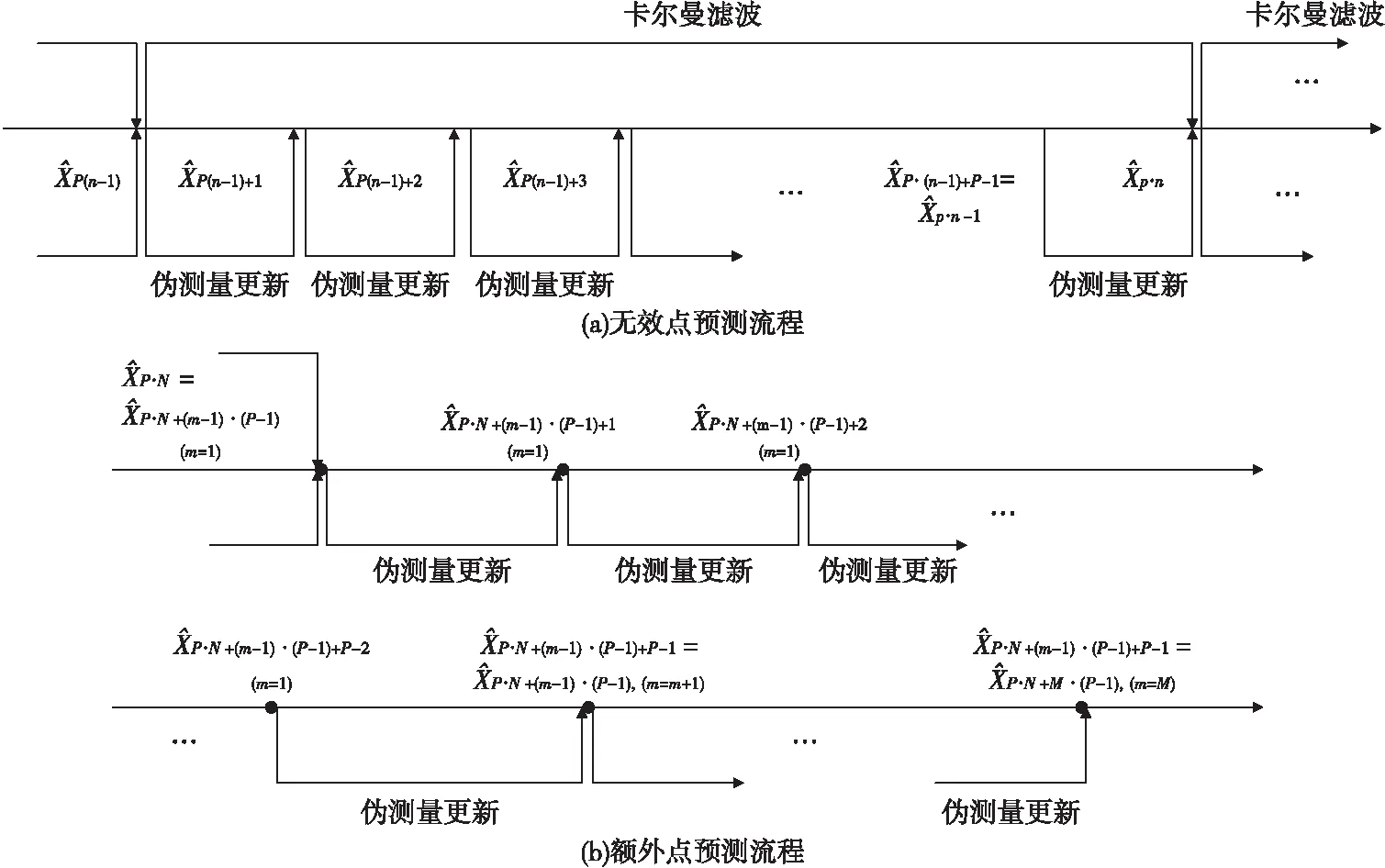
图3 部分预测流程Fig.3 Partial prediction process

在进行上述预测和更新流程后，可得到高精度、高测量数据更新速率、具有额外预测点数的高度信息，该信息可用于实现引信高精度炸点控制。

3 仿真分析

3.1 模拟数据仿真结果

假设弹道起点高度为160 m，初始速度1 000 m/s，先进行加速度为10 m/s2的匀加速运动，后在第105 ms和第120 ms时因机动原因，分别开始进行变加速和匀速运动，如图4所示。

图4 测量与滤波轨迹Fig.4 Measurement and filter trajectory

仿真验证算法对高度测量信息量测精度及更新速率的提升效果，拟将更新速率从0.5 ms提高至0.1 ms。设信号测量误差服从均值为0、方差为9的正态分布，采用本文提出的包含无效点滤波的预测算法，忽略噪声相关性，选用匀加速运动模型进行滤波计算，在滤波的结果上，额外进行64点预测，即可额外预测约6.4 m的高度数据。蒙特卡洛仿真次数取100次，仿真结果如图4—图8所示。

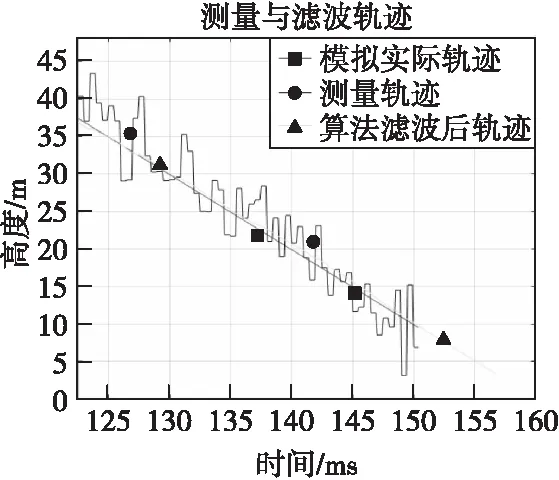
图5 测量与滤波轨迹局部放大图Fig.5 Measurement and fusion of the fusion trajectory

图4、图5为轨迹和滤波融合处理结果示意图，图6—图8为处理前后位置信息误差对比图。

由图4、图5可知，本文算法可将采样间隔从0.5 ms提高到0.1 ms，距离分辨率从0.5 m提高到0.1 m，且额外预测了约6.4 m之后的高度信息。

图6、图7、图8分别为信号处理前后高度、速度和加速度信息误差对比图。相比于原始信息，使用本文提出的弹道高度预测算法可以显著降低测量误差，融合前后误差统计如表1所示。

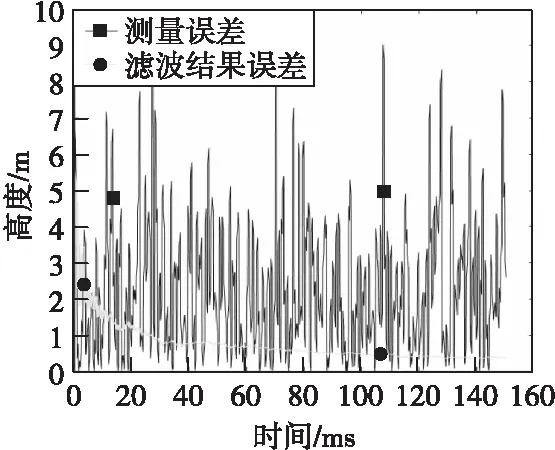
图6 高度信息绝对误差Fig.6 Altitude information absolute error

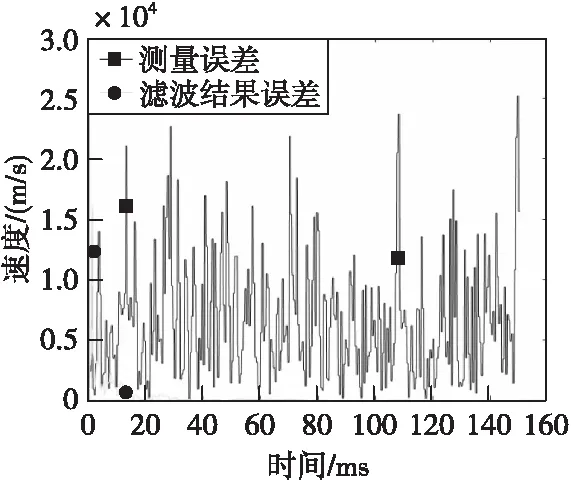
图7 速度信息绝对误差Fig.7 Velocity information absolute error

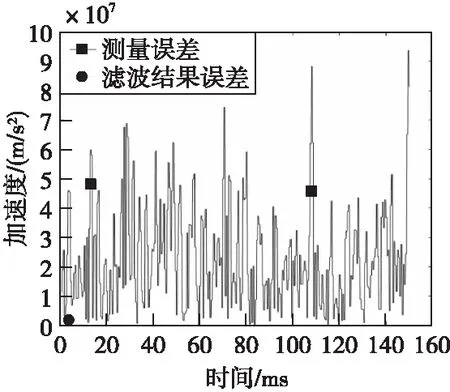
图8 加速度信息绝对误差Fig.8 Acceleration information absolute error

表1 滤波前后误差对比Tab.1 The comparison of the error of filtering

3.2 带环境噪声信号仿真结果

仿真模拟信号受到随机环境噪声时的滤波效果，噪声均值为0，仿真得到在不同强度的环境噪声下算法对检测误差的改善效果，结果如表2所示。

由表2数据可知，当量测信息持续受到环境噪声干扰时，算法仍有较好的收敛效果。

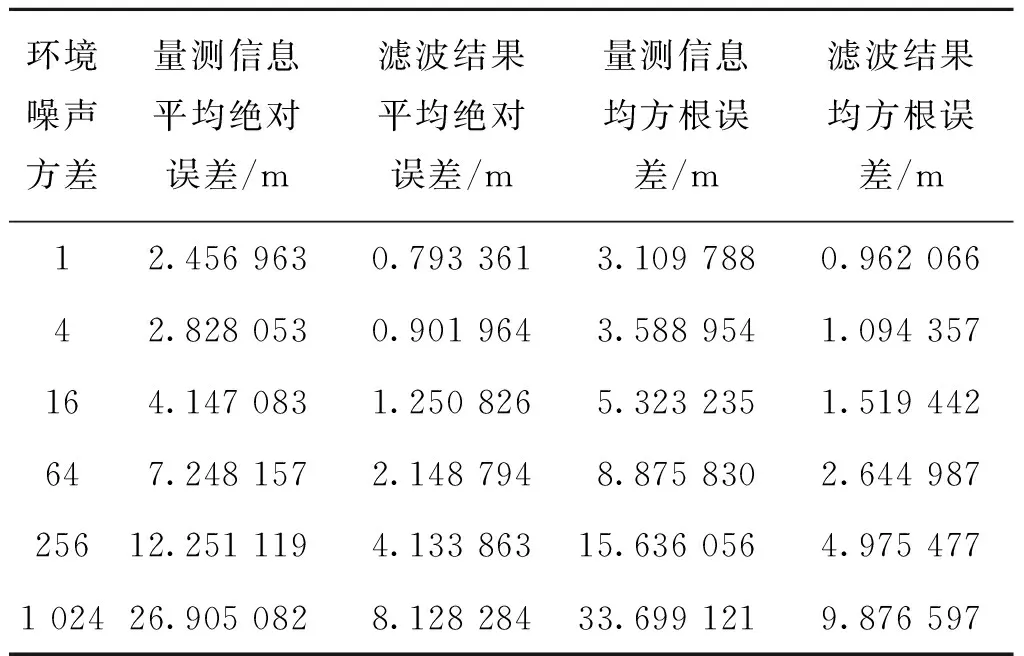
表2 不同环境噪声下误差对比Tab.2 Error comparison of different ambient noise

当环境噪声方差小于4时，滤波结果均方误差相比无环境噪声时仅提高不到20%，可以认为此时环境噪声对算法效果无明显影响。

当环境方差达到256时，滤波结果均方根误差约4.98 m，远大于原始量测信息的均方根误差约3 m。此时，可认为算法失去有效判断炸点的能力。

图9—图12为环境噪声方差为64时的滤波结果，仿真验证了在环境噪声的影响下算法的有效性。

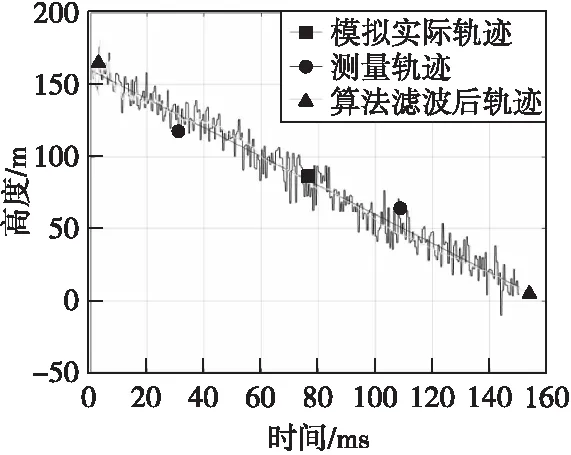
图9 测量与滤波轨迹Fig.9 Measurement and filter trajectory

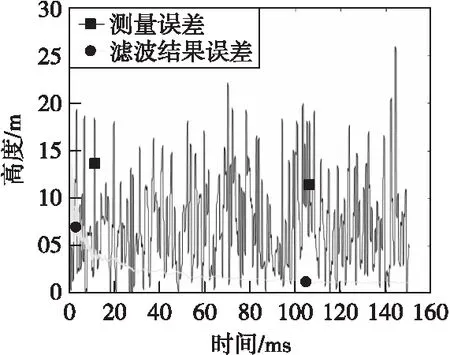
图10 高度信息绝对误差Fig.10 Altitude information absolute error

图11 速度信息绝对误差Fig.11 Velocity information absolute error

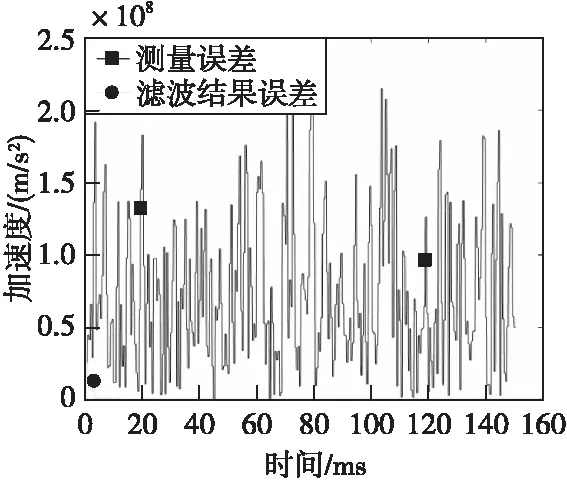
图12 加速度信息绝对误差Fig.12 Acceleration information absolute error

3.3 带干扰点信号仿真结果

仿真模拟测量信息受到点干扰时的滤波效果，设置量测信息受到方差为4的随机环境噪声影响，同时受到4处距离干扰，干扰持续时间分别为2，1.5，2，1 ms，干扰平均偏移为45 m，并且信号从第105 ms开始存在持续4 ms的漏点，导致持续上报相同的距离信息，仿真结果如图13—图17所示。

图13 测量与滤波轨迹Fig.13 Measurement and filter trajectory

图14 测量与滤波轨迹局部放大图Fig.14 Measurement and filter of the fusion trajectory

图15 高度信息绝对误差Fig.15 Altitude information absolute error

图16 速度信息绝对误差Fig.16 Velocity information absolute error

图17 加速度信息绝对误差Fig.17 Acceleration information absolute error

图13、图14为轨迹和滤波结果示意图，图15—图17为滤波前后高度、速度、加速度信息误差对比图。由图14可见，本文算法能够在提高测量数据更新速率、提升预测精度、消除漏点的同时，对弹道高度测量中存在的干扰点具有良好的抑制效果。加干扰点和漏点信号的滤波前后误差统计如表3所示。

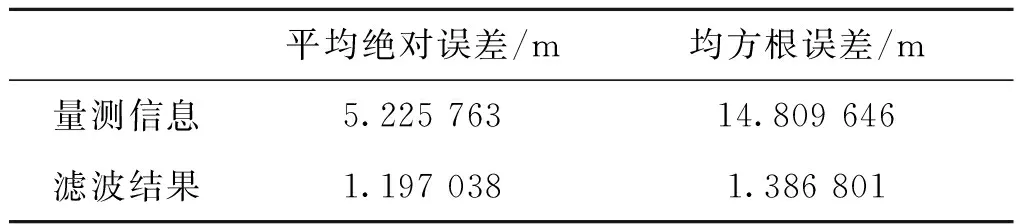
表3 滤波前后误差对比Tab.3 The comparison of the error of filtering

相比于传统插值算法，本文算法具有实时性高、抗噪能力强等优点，可有效提升对地近炸引信对地测高精度与抗干扰能力。

4 结论

本文提出一种包含无效点滤波的弹道高度预测算法。该算法通过引入无效点概念，建立流程将探测漏点、受干扰点和需插值点设置不同类型的无效点；为抗持续干扰可以设置任意数目和数据更新速率的额外预测点；分别对无效点和额外预测点利用系统状态方程、扩展卡尔曼滤波、伪测量技术等算法进行弹道高度信息预测。

仿真验证结果表明，本文算法在提高数据更新速率、消除漏点干扰、弹道高度额外点预测、降低随机噪声干扰等方面效果显著，经算法处理的弹道高度信息平均绝对误差和均方根误差相比原始信号均有明显降低。相比于传统插值算法，本文算法具有实时性高、抗噪能力强等优点，可用于无线电引信识别与控制技术领域，能有效改善弹道高度测量中观测信号可能出现的有效数据缺失、数据更新速率低，因环境噪声和干扰造成测距精度下降的问题。