M序列编码调频定距引信抗干扰特性

熊雪瑶，牛兰杰，2，马 捷，2，李维山

(1. 西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

调频无线电引信因其定距精度高、抗干扰能力强等优点[1]，在各国得到广泛的应用。但干扰技术的发展对引信的战场生存及毁伤能力带来了严峻的挑战。国外引信干扰机具有成功干扰连续波多普勒、调频等体制无线电引信能力[2]。

针对引信抗干扰技术，国内开展了大量的相关研究工作。文献[3]对脉冲定距引信高频载波进行0/π调相，但该方法对于调频连续波信号定距有很大的局限性。文献[4—5]提出了基于目标联合特征提取的引信抗干扰方法和引信抗周期调制干扰信号的方法，但是新一代的基于射频存储(DRFM)转发的干扰机[6-7]能直接提取引信发射信号特征并作为干扰，使以上方法抗干扰能力大幅下降。针对该问题，文献[8]提出一种双调制率调频引信对抗DRFM干扰，但该方法抗干扰效果提升较小。本文提出一种基于M序列编码技术的调频无线电引信定距方法，降低引信目标回波信号与干扰信号的相关性，提升抗干扰性能。

1 基于模糊函数的引信抗干扰能力评估

模糊函数是对信号进行分析研究和波形设计的有效工具，也是分析、比较信号处理系统优劣的重要手段[9]。通过模糊函数可以研究引信系统具有什么样的分辨力、模糊度、测量精度和抑制干扰能力。引信向目标发射信号，发射信号经过目标反射形成回波信号。回波信号的波形与发射信号相同，但有不同的时延τ和不同的频偏v(即多普勒频率)，因此模糊函数经处理后变换到时延-频偏平面，是τ和v的二维响应，表征了发射信号与目标回波信号的相关性。

单周期模糊函数的正型定义式为

(1)

式(1)中，c(t)为周期调制连续波信号，即c(t)=c(t-nT)(n=0,±1,±2，…)，ξ为多普勒频率。

对于线性调频信号，其相比于脉冲信号发射的峰值功率较低，非合作截获接收机的截获距离少，同时频率调制将发射能量扩散在一个大的调制带宽内，提供了良好的距离分辨力。模糊图的多普勒轴显示的频率为往返延时引起的差频和目标运动引起的多普勒频率的代数和。三角波线性调频信号单周期模糊函数如图1所示。

图1中，整个3D模糊图关于原点成中心对称，由一个完整的X型和两个可以构成一个完整的X型“斜刀刃”的两个半X型“斜刀刃”组成。同一个延迟τ对应符号相反绝对值相同的两个频移ξ，这两个频移是由对称三角波调频信号的上下扫频段产生的。

周期模糊函数与单周期模糊函数的关系为

(2)

即多周期模糊函数等于其单周期模糊函数乘以与复包络和时延无关的表达式得到。三角波线性调频信号多周周期模糊函数如图2所示。

图1、图2中，模糊函数是关于时延和多普勒频率的函数。其幅度代表了其分辨不同速度和距离的目标的能力。

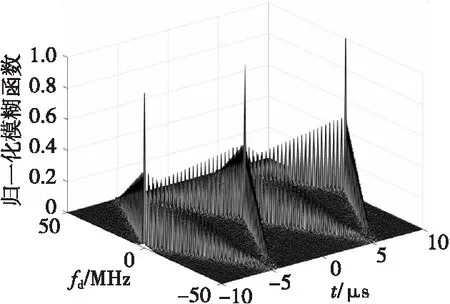
图1 三角波线性调频信号单周期模糊函数Fig.1 Single period ambiguity function diagram of triangular wave linear frequency modulation signal

图2 三角波线性调频信号多周期模糊函数Fig.2 Multi period ambiguity function diagram of triangular wave chirp signal

2 基于M编码信号提升引信抗干扰性能

利用M序列对三角波线性调频信号的载频调制，产生载频不断跳变的M编码三角波线性调频信号。

调制信号发生器产生频率为fM的三角波信号，M序列发生器产生M序列编码对压控振荡器调制，产生载频变化的三角波线性调频信号，经天线向目标发射。与此同时将一部分发射信号送至混频器作为与回波信号混频的本振信号。倍频器将三角波线性调频信号频率倍频，得到2fM和4fM频率的信号，分别用作二次混频器的基准信号。发射信号经过目标反射后被天线接收，与本振信号混频，得到含有距离速度信息的差频信号。该差频信号包含多普勒信号fd和被多普勒信号调制的三角波调制频率各次谐波信号(nfM±fd)。带通滤波器分别选取2fM和4fM谐波信号，与基准信号2fM和4fM进行二次混频。最后对多普勒信号进行特征提取，包络检波等，进而最终推动执行级。过程如图3所示。

图3 M编码三角波线性调频引信定距原理Fig.3 The distance determination principle of M-coded triangular wave linear FM fuze

M序列编码调频无线电定距引信在第m+1个调频周期内发射信号SI,m+1：

SI,m+1=A0exp{j[2π(fm+1(t-mT)+

mT≤t≤(m+1)T,

(3)

式(3)中，A0为信号幅度；fm+1为第m+1个调频周期的调频中心频率，其大小表示为fm+1=f0+bm+1·Δf，其中f0为起始调频频率，bm+1为频率跳变编码序列，Δf为跳频分量，K为调制斜率，Δφm为第m个调频周期的相位。

存在一个径向速度为v，初始径向距离为R的目标，即回波延迟为τ=2(R-vt)/c，c为光速。回波信号为

Sr，m+1=A0Krexp{j[2π(fm+1(t-mT-τ)+

(4)

式(4)中，Kr为传播衰减常数。

(5)

式(5)中，B为调制频偏，T为调制周期。相应的调频信号的相位为

(6)

M编码三角波线性调频信号经过弹目之间的双程传输后，在混频器中回波信号与发射信号混频得到的差频信号为

(7)

所以，在一个调频周期内，差频信号为

(8)

对于双极性M编码三角波线性调频引信，其发射信号、回波信号及差频信号如图4所示。

图4 M编码三角波线性调频引信的发射信号，回波信号及差频信号Fig.4 Diagram of transmitted signal, echo signal and differential frequency signal of M-coded triangular wave LFM fuze

对于动目标，在各个调频周期内，其双程传输产生的时延τ有差异。在第m个调频周期内，时延τ为

(9)

式(9)中，Rm表示第m个调频周期起始时刻引信与目标之间的距离，Rm=R+vTm。

在第m个调频周期内，差频信号为

(10)

差频信号频率与目标的距离、速度都有关。用fb表示差频频率，用fd表示多普勒频率：

(11)

(12)

因此，在第m个调频周期内，差频信号简化为

(13)

(14)

M编码三角波线性调频信号所有调频周期对应的差频信号经过采样后是一个与时延和多普勒频率有关的二维离散信号。可绘出M编码三角波线性调频信号的模糊函数图，对该信号的自相关性进行分析。

发射信号重新写作

exp[j2πbm+1·Δf(t-mT)]，

mT≤t≤(m+1)T。

(15)

M编码三角波线性调频信号等同于多周期三角波线性调频信号与频率编码信号时域相乘得到的信号波形，μ(t)=μ1(t)·μ2(t)，根据模糊函数变换关系中的相乘特性，组合信号的模糊函数为

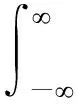
(16)

令f=f-Y,Y=Y-q代入式(16)得：

(17)

式(17)证明时域上两个相乘信号的模糊函数等于这两个信号本身的模糊函数在多普勒轴上的卷积。M编码三角波线性调频信号的模糊函数等于多周期三角波线性调频信号与M序列编码信号的模糊函数在多普勒轴上的卷积。

编码序列的子载波数为M个，当其单个编码持续时间与三角波线性调频信号单个周期相同，且fi=f0+bi·Δf时，该编码信号的复包络为

(18)

式(18)中，u(t)为长度为T的矩形脉冲。代入模糊函数表达式，得到频率编码信号模糊函数：

(19)

式(19)中，χu(τ,ξ)为矩形脉冲信号u(t)的自相关函数，

χu(τ,ξ)=

(20)

双极性M编码的模糊函数如图5所示。

图5 M序列模糊函数Fig.5 Ambiguity functionof M-sequence

M编码三角波线性调频信号模糊函数:

(21)

根据式(21)画出M编码三角波线性调频信号的模糊函数如图6所示。

图6 M编码三角波线性调频信号模糊函数Fig.6 Ambiguity function diagram of M-coded triangular wave linear FM signal

与图2对比可知，频率编码后的M编码三角波线性调频信号自相关性更强，其具有良好的相邻目标的距离和速度分辨能力以及单目标测距测速精度。

3 仿真验证

设定调频探测器的指标：中心频率24 GHz，调制频偏为50 MHz，调频周期为10 μs，模糊距离为1 500 m。

采用M序列编码，码元宽度为固定值对振荡器的中心频率进行调制，中心频率的跳变时间为10 μs，频率跳变间隔为23.7～24.0 GHz。

无线电引信的信号检测过程可用门限检测描述，即为一种能量检测。因此仿真利用不同周期、不同位数，M序列编码前后信号与干扰的能量相关性作为抗干扰性能的评价标准。仿真得到信号与干扰的相关图，相关图的幅度最大值为相关性指标。相关性指标越大，信号与干扰的相关性越强，引信处理回波信号时越易受到干扰影响，引信抗干扰效果越弱。

射频存储转发器作为干扰器，能够存储发射信号的几个周期，经处理后作为干扰信号向引信接收机发射，通过速度牵引、距离门牵引对目标回波信号实施干扰，其存储并处理发射信号的一个周期，表达式为

(22)

(23)

分别对M编码三角波线性调频信号进行2，3，4，5位编码，得到2n-1周期，即3周期，7周期，15周期，31周期M编码三角波线性调频信号。常规编码方式包括格雷码、BCD码、余3码等。由于格雷码是一种错误最小化的编码方式，其循环和单步特性消除了随机取数时出现重大错误的可能，反射和自补特性使得对其进行求反操作也非常方便，因此对M编码使用格雷码编码方式。利用格雷码规则，将其对应的数值与跳频点中心频率一一对应，从而得到各频率跳变值。

多周期M编码信号时频图如图7所示。分别得到不同周期数，三角波线性调频引信目标回波信号与射频存储转发器发射的干扰信号的相关性指标与M编码三角波线性调频信号与射频存储转发器发射的干扰信号的相关性指标，如图8所示。

图7 多周期M编码信号时间-频率图Fig.7 M-coded signal time-frequency diagram

图8 信号与干扰相关图Fig.8 Correlation diagram of frequency hopping signal and interfere

如表1所示，相较于典型未编码体制无线电引信，在分别进行2，3，4，5，6位编码时，M编码体制无线电引信的相关性指标分别为原来的1/3，1/7，1/15，1/18.618 6，1/20.554 0。引信接收机分辨信号与干扰的能力提升了3，7，15，18.618 6，20.554 0倍，

表1 信号与干扰相关性指标Tab.1 Correlation index of signal and interfere

M编码信号编码位数越多，信号周期数越大，射频存储转发器产生的干扰信号与回波信号的相关性越弱，引信抗干扰效果越好。但随着编码位数增多，伪码周期数增大，引信抗干扰效果提升增长效果变缓，如图9所示。

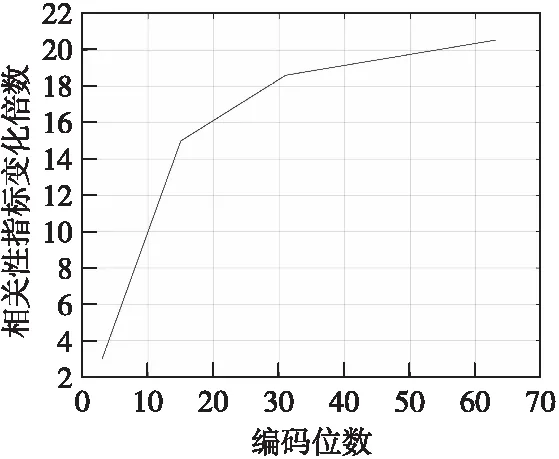
图9 编码位数与相关性指标关系图Fig.9 Changes between coding digits and correlation

相比于新体制双调制频率引信，M编码体制多跳频无线电引信接收的干扰与回波信号的相关性更小，且引信接收机可降低幅度门限值，其抗DRFM干扰成功率更高。

射频存储转发器存储并转发信号的周期数对引信的抗干扰能力有不同影响。不同周期数与引信相关性指标变化倍数的仿真结果如表2所示。

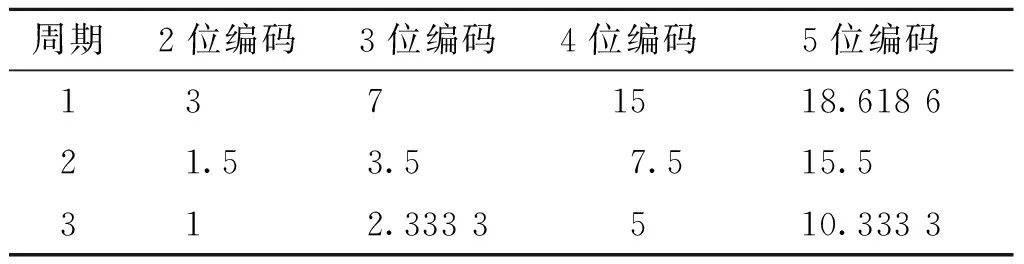
表2 周期数与相关性指标变化倍数关系Tab.2 Changes between cycles and correlation index

射频存储转发器存储发射信号并作为干扰信号的周期数越少，干扰与回波信号相关性越弱，抗干扰性能越强。

4 结论

本文对M序列编码三角波线性调频定距引信抗干扰特性进行了研究，对该引信的工作原理进行了分析，信号处理过程进行了理论推导；计算得到了M编码信号的模糊函数并进一步推导了M编码三角波线性调频信号的模糊函数，并分析了基于M序列编码的三角波线性调频定距引信抗干扰性能。仿真验证表明：码元宽度一定时， M编码信号编码位数越多，伪码周期数越大，射频存储转发器产生的干扰信号与回波信号的相关性越弱，引信抗干扰效果越好；射频存储转发器存储发射信号并作为干扰信号的周期数越少，干扰与回波信号相关性越弱，抗干扰效果越好。在实际工程应用中，应综合考虑抗干扰性能需求与载频跳变点数的可实现性以选择合适的编码位数，并在此基础上，进一步研究适用于调频定距引信的编码方式，以达到对抗新型DRFM引信干扰机的目的。