全电子安全系统失效率计算
2023-03-07汪仪林马秋华
汪仪林,马秋华
(西安机电信息技术研究所,陕西 西安 710065)
0 引言
按照GJB 373B—2019《引信安全性设计准则》[1]的要求,引信安全系统除了满足相关的设计要求外,还应对解除保险/解除隔离流程开始前、流程中直至安全分离的各阶段进行安全失效率的计算。机械、机电隔离型安全系统在GJB/Z 29A—2003《引信典型故障树手册》[2]中给出了相应的计算方法,文献[3]给出了某些可信环境对安全失效率的影响。对于全电子安全系统安全失效率的分析,目前尚无较为完整的计算方法。本文根据文献[4]《电和电磁环境对引信全电子安全系统的影响分析》得出的典型的电/电磁环境在高压电容上的电压和雷管两端的电压及安全失效率的计算结果,由全电子安全系统的框图A,得出非工作、通电、一个静态开关闭合和两个静态开关闭合等状态下的安全失效率计算公式,举例说明了计算方法,给出了另两种典型的全电子安全系统框图(全电子安全系统的框图B、C)的安全失效率的计算结果,说明了框图级全电子安全系统安全失效率的计算和比较方法。
1 全电子安全系统失效率计算原理和方法
1.1 典型全电子安全系统的框图
参照美国引信年会论文[5]中给出的全电子安全系统原理图,得到的框图如图1所示。

图1 全电子安全系统原理框图AFig.1 The principle A of electronic safety-and-arming system
其工作过程为:解保环境识别k1识别第一解保环境后,输出控制信号,驱动静态开关1闭合,接通电源地;解保环境识别k2识别第二解保环境,逻辑控制器k4对k1、k2输出进行时序判断,在k1开启的时间窗ΔT内检测到k2输出,则控制阻断器k3释放,静态开关2闭合,接通电源;在满足规定的延时要求后,产生交替变化的信号控制动态开关,高压变换器在交变信号的驱动下进行高压变换,开始对高压电容充电,解除隔离。
令图中两个静态开关、动态开关非工作状态正常工作的概率为p11、p21、p31,非工作状态发生短路故障的概率为p1d1、p2d1、p3d1,工作状态发生短路故障的概率为p1d2、p2d2、p3d2。
环境识别k1、环境识别k2、阻断器k3误输出的概率pk1d、pk2d、pk3d,分别为器件故障导致误输出的概率(pk1k、pk2k、pk3k)与识别错误导致误输出的概率(pk1s、pk2s、pk3s)之和。
逻辑识别k4误输出的概率pk4d,其中器件故障导致控制误输出的概率pk4k,对环境识别1检测虚警率pk4s1、对环境识别2检测虚警率pk4s2;延时时间小于预定时间的概率pk4T;有效时间窗和工作时间之比为ΔT/T。
1.2 全电子安全系统安全失效率计算
由于不同的武器系统解除保险/解除隔离流程和发射过程的事件有所不同,为不失普遍性,根据全电子安全系统的特点,按照4个状态分析安全失效率:1)非供电P11;2)解除保险和解除/隔离流程开始前的通电状态P21;3)一个静态开关闭合P31;4)两个静态开关闭合P41。
根据全电子安全系统的特点,GJB 373B中“在预定的解除保险和解除隔离流程开始前,防止引信解除隔离或作用的失效率应不大于百万分之一”对应于1)、2)两个状态下的安全失效率。
1.2.1未通电状态全电子安全系统安全失效率
未通电状态,安全失效率为
P11=Pin11+Pout11=Pini11+Ping11+
Pinv11+Pouti11+Poutg11,
(1)
式(1)中,Pin11为输入端引入电能量导致的安全失效率,Pout11为输出端引入电能导致的安全失效率,Pini11为输入端由于电流馈入导致的安全失效率,Ping11为输入端由于静电导致的安全失效率,Pinv11为输入端由于电压瞬变导致的安全失效率,Pouti11为输出端由于电流馈入导致的安全失效率,Poutg11为输出端由于静电导致的安全失效率。
Poutg11=P(Ucg)+P(Udg),
Pouti11=P(Uci)+P(Udi),
式中,Ucg为静电激励在高压电容上产生的电压,Udg为静电激励在雷管上产生的电压,Uci为电流注入在高压电容上产生的电压,Udi为电流注入在雷管上产生的电压。
文献[4]分析了输出回路静电、电流两种馈入方式在高压电容和雷管上建立的电压,得出了在人体静电和可信电流激励下,P(Ucg)、P(Uci)、P(Udg)、P(Udi)都在10-10以下,可忽略其影响,故式(1)可简化为
P11=Pin11+Pout11=Ping11+Pini11+Pinv11,
Ping11=p11×p21×p31×P(Ug123)+
p1d1×p21×p31×P(Ug23)+
p11×p2d1×p31×P(Ug13) +
p11×p21×p3d1×P(Ug12)+
p1d1×p2d1×p31×P(Ug3)+
p1d1×p21×p3d1×P(Ug2)+
p11×p2d1×p3d1×P(Ug1)+
p1d1×p2d1×p3d1×P(Ug),
(2)
式(2)中,P(Ug123)为3个开关均处于开启时,由静电导致的安全失效概率;P(Ug23)为开关1出现短路故障时,静电导致的安全失效概率;P(Ug13)为开关2出现短路故障时,静电导致的安全失效概率;P(Ug12)为开关3出现短路故障时,静电导致的安全失效概率;P(Ug3)为开关1、开关2出现短路故障时,静电导致的安全失效概率;P(Ug2)为开关1、开关3出现短路故障时,静电导致的安全失效概率;P(Ug1)为开关2、开关3出现短路故障时,静电导致的安全失效概率;P(Ug)为3个开关出现短路故障时,静电导致的安全失效概率。
根据文献[4]的计算可知P(Ug3)、P(Ug2)、P(Ug1)、P(Ug23)、P(Ug13)、P(Ug12)、P(Ug123)均小于10-10,故可以将上式简化为
Ping11≈p1d1×p2d1×p3d1×P(Ug)。
类似地可得
Pini11≈p1d1×p2d1×p3d1×P(Ui),
(3)
Pinv11≈p1d1×p2d1×p3d1×P(Uv),
(4)
式中,P(Ui)为3个开关出现短路故障或解除时,由电流馈入导致的安全失效概率;P(Uv)为3个开关出现短路故障或解除时,由电压瞬变导致的安全失效概率。
则有
P11≈p1d1×p2d1×p3d1×(P(Uv)+P(Ui)+P(Ug))。
(5)
根据文献[4]可知,当三个开关导通时,GJB 151B规定的电流注入和电压串扰可导致安全失效,故
P11=p1d1×p2d1×p3d1。
1.2.2通电状态下全电子安全系统安全失效率计算
通电状态,静态开关未闭合,安全失效率P21为
P21=Pin21+Pout21+Pk21,
(6)
式(6)中,Pin21为通电状态下输入端引入电能量导致的安全失效;Pout21为通电状态下输出端引入电能导致的安全失效,由文献[4]的计算知,可忽略;Pk21为动态开关启动升压的概率。
同1.2.1节分析,将3个开关均处于导通状态和开启升压作为安全失效,则有
P21≈Pk123d1+Pk21,
(7)
式(7)中,Pk123d1为通电状态3个开关均导通的概率。
为了方便说明,先分别给出静态开关1、2,动态开关3分别导通的框图,见图2—图4,再得出3个开关均导通和启动升压的框图,见图5、图6。
用Pk1d、Pk2d和Pk3d分别表示静态开关1闭合的概率、静态开关2闭合的概率和动态开关3闭合的概率。
1)计算静态开关1闭合的概率Pk1d
根据图1,得出静态开关1闭合概率的计算框图如图2所示。

图2 静态开关1闭合的框图Fig.2 The diagram of static switch 1 shut
根据串并联关系[6],可得
Pk1d=1-(1-pk1d)×(1-p1d2)=
pk1d+p1d2-p1d2×pk1d,
(9)
即
Pk1d=pk1k+pk1s+p1d2-p1d2×(pk1k+pk1s)。
忽略高阶小量可得:PK1d≈pk1k+pk1s+p1d2。
2)计算静态开关2闭合的概率Pk2d
根据图1,静态开关2闭合的概率计算框图如图3所示。

图3 静态开关2闭合的框图Fig.3 The diagram of static switch 2 shut
由图3的串并联关系,并忽略高阶小量可得:
(10)
3)计算动态开关3闭合的概率Pk3d
根据图1得到动态开关导通的概率计算框图如图4所示。

图4 动态开关导通的框图Fig.4 The diagram of dynamic switch shut
由图4的串并联关系,并忽略高阶小量可得
(11)
由于开关1、2、3导通不独立,三个开关均导通,忽略高阶小量的框图如图5所示。
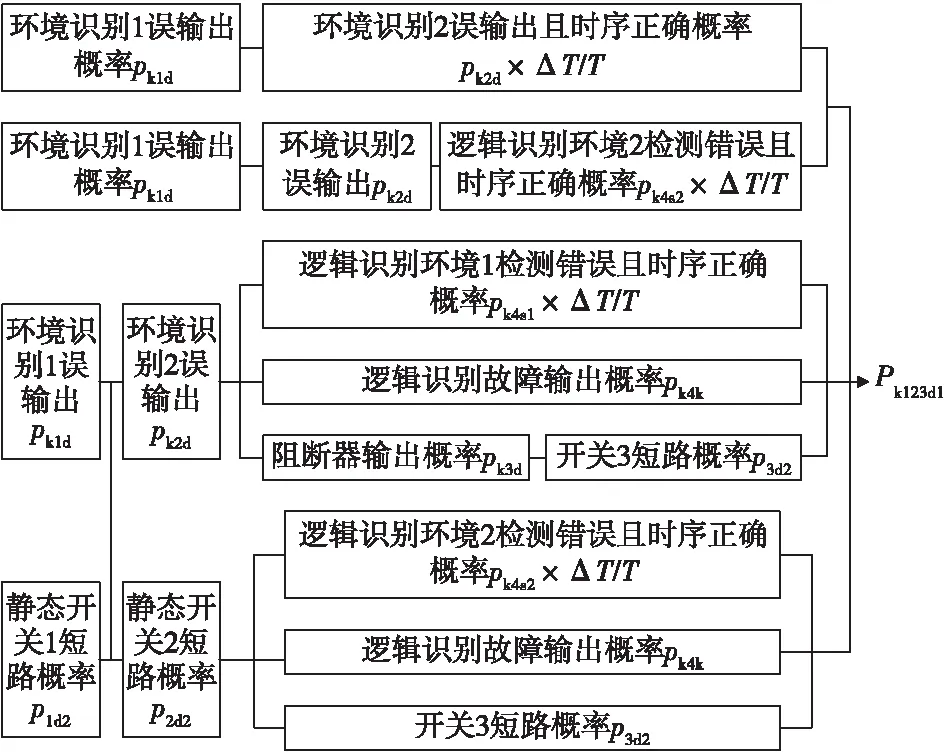
图5 开关均导通的框图Fig.5 The diagram of all switches shut
由图5的串并联关系,并忽略高阶小量可得

(12)
根据图1得到启动升压的框图如图6所示。
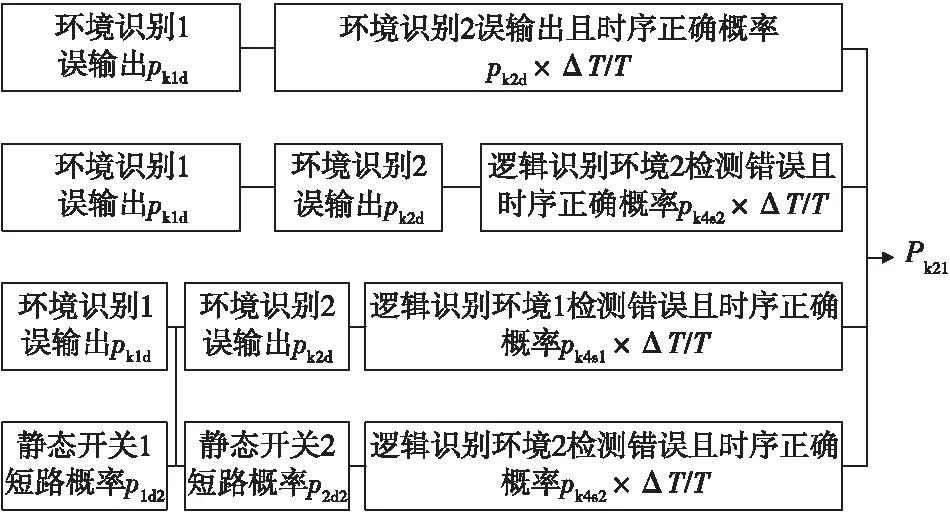
图6 启动升压的框图Fig.6 The diagram of the voltage step up
启动升压的概率:
(13)
将式(12)、式(13)代入式(7),合并相同的项后,可得通电后安全失效率。
1.2.3静态开关1闭合后的安全失效率
静态开关1闭合后的安全失效率P31为
P31=Pin31+Pout31+Pk31,
(14)
式(14)中,Pin31为静态开关1闭合状态下输入端引入电能量导致的安全失效率,Pin31≈Pk123d2;Pout31为静态开关1闭合状态下输出端引入电能导致的安全失效率,可忽略;Pk31为静态开关1闭合状态下启动升压的概率
而确实为南宋闽刻的三卷本《山谷琴趣外篇》则因其先天的缺陷而频遭学者讥议。朱孝臧《彊村丛书》跋此书云:“卷中讹文脱字,往往而有,题尤芟节太甚,或乖本恉。”[1]277饶宗颐《词集考》亦批评此本“词数仅得一卷之半,讹文夺字,芟节题序,祝穆讥为俗本者也”[2]54。但是这个版本由于收录不足黄庭坚存世词作总数之半,所收词作全部见于嘉靖本系统中,因此,从著作权角度看此本还是比较可信的。此外,南宋乾道麻沙本《类编增广黄先生大全文集》有词一卷,所收篇目及内容与《琴趣外篇》本大体相同。二者都刻于福建,都属坊刻本,可能有某种渊源关系。
同前所述,可将式(14)简化为
P31≈Pk123d2+Pk31,
(15)
式(15)中,Pk123d2为静态开关1闭合状态下3个开关均导通的概率,Pk31为静态开关1闭合状态下启动升压的概率。
由图5,令图中静态开关1闭合为必然事件,可得3个开关均导通忽略高阶小量的框图如图7所示。

图7 静态开关1闭合下,静态开关2、3闭合的框图Fig.7 The diagram of static switch 2 and 3 closed while static switch 1 shut
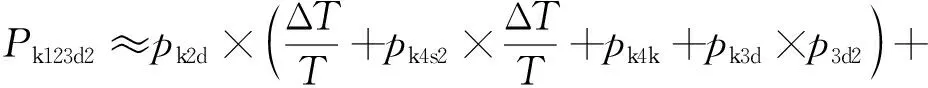
(16)
由图6,令图中静态1闭合为必然事件,静态开关1闭合状态下启动升压的概率PK31的框图如图8所示。

图8 静态开关1闭合下,启动升压的框图Fig.8 The diagram of the voltage step up while static switch 1shut
(17)
将式(16)、式(17)代入式(15),合并相同的项后,可得静态开关1闭合后安全失效率。
1.2.4静态开关均闭合后的安全失效率计算
P41=Pin41+Pout41+Pk41,
(18)
P41≈Pk123d3+Pk41,
(19)
式(19)中,Pk123d3为静态开关1、2闭合状态下3个开关均处于闭合状态的概率,Pk41为静态开关1、2闭合状态下启动升压的概率。
Pk123d3=pk4k+p3d2+pk4T,
Pk41=pk4T。
(20)
代入式(19),合并相同的项后,可得静态开关均闭合后的安全失效率。
2 元器件失效率计算
在安全失效率计算中,涉及元器件非工作状态和工作状态两种情况,非工作状态根据GJB/Z 108A—2006《电子设备非工作状态可靠性预计手册》[7]进行预计,工作状态根据GJB/Z 299C《电子设备可靠性预计手册》[8]进行预计。
2.1 非工作状态失效率计算
静态开关1、2和动态开关、环境识别控制通常采用半导体分立器件,其非工作失效率预计模型为
λNp=λNbπNEπNQπNTπNcycπNr。
(21)
环境识别控制、逻辑识别控制、阻断器等通常采用单片数字电路、微处理器、存储器、单片模拟电路等,其非工作失效率预计模型为
λNp=λNbπNEπNQ(πNT+πNF)πNcycπNL,
(22)
式(22)中,λNp为非工作失效率,10-6/h;λNb为非工作基本失效率,10-6/h;πNE为非工作环境系数;πNQ为非工作质量系数;πNT为非工作温度系数;πNcyc为设备电源通断循环次数;πNr为产品性能额定值系数;πNL为产品成熟度系数;πNF为封装系数。
各元器件非工作状态失效率:PfN=1-e-λNpTN≈λNpTN,TN为非工作时间,若存贮期为15年,TN=131 400 h。
为了方便说明,将相关参数列于表1。

表1 非工作状态器件失效率参数表Tab.1 Table of failure rate ofnon-operation state device
2.2 工作状态失效率计算
静态开关1、2和动态开关常用半导体分立器件,其工作状态失效率预计模型为
λp=λbπEπQπAπCπrπS2。
(23)
识别控制器常用单片数字电路、微处理器、存储器、单片模拟电路等构成,其工作状态失效率预计模型为
λp=πQ[C1πTπv+(C2+C3)πE)πL,
(24)
式(24)中,λp为工作失效率,10-6/h;λb为基本失效率,10-6/h;πA为应用系数;πE为环境系数;πQ为质量系数;πT为温度应力系数;πv为电压应力系数;πr为产品性能额定值系数;πC为结构系数;πL为成熟度系数;πF为封装系数;C1、C2为电路复杂度失效率;C3为封装复杂度失效率。
各元器件工作失效率:Pf=1-e-λpT≈λpT,工作时间为等效500 h。相关参数如表2、表3所示。

表3 半导体集成电路失效率预计表Tab.3 Table of estimated failure rate of semiconductor integrated circuit
2.3 静态开关、动态开关短路失效率计算
GJB/Z 299C《电子设备可靠性预计手册》[8]中给出了元器件不同失效模式的频数,将相关数据列于表4。
式(1)—式(4)中的p1d1、p2d1、p3d1用下式计算:
pid1=PfN×Nd(i=1,2,3)。
式(5)—式(11)中的p1d2、p2d2、p3d2用下式计算:
pid2=Pf×Nd(i=1,2,3)。
式(5)—式(17)中的pk1k、pk2k、pk3k、pk4k由选用器件的失效率和给出有效控制输出故障的频数计算。

表4 元器件失效频数表Tab.4 Table of failure frequency of device
3 全电子安全系统失效率算例
参照1.1节给出的全电子安全系统,其静态开关1采用双极型晶体管,静态开关2采用晶闸管,动态开关采用硅场效应晶体管;环境识别1采用光耦开关,环境识别2采用传感器和模拟电路,阻断器采用MOS触发器,逻辑识别与控制采用MOS微处理器;环境识别2有效时间窗和工作时间之比为1/10。
3.1 未通电状态全电子安全系统安全失效率计算
计算p1d1、p2d1、p3d1:
由表1得静态开关1双极型硅管λNP=0.720×10-3,T=15年,PNf=0.001 25,查表4其短路失效的频次为36.3%,得:p1d1=0.001 25×0.363=4.54×10-4;
由表1得静态开关2晶闸管λNP=0.157 80,T=15年,PNf=0.020 74,查表4短路失效的频次为40%,p2d1=0.020 7×0.40=0.830×10-2;
由表1得动态开关硅场效应晶体管λNP=0.053 85,T=15年,PNf=0.007 07,查表4短路失效的频次为35%,p3d1=0.007 07×0.35=2.475×10-3;p11≈4.54×0.830×2.475×10-9=9.33×10-9。
因此,通常情况下,认为全电子安全系统具有更高的安全性。
3.2 通电状态下全电子安全系统安全失效率计算
1)计算p1d2、p2d2、p3d2、pk1k、pk2k、pk3k、pk4k
由表2得静态开关1双极型硅管λP=1.230 9,T=500 h,Pf≈6.15×10-3,由表4得短路失效的频次为36.3%,p1d2=6.15×10-3×0.363=2.23×10-3;
由表2得静态开关2晶闸管λP=1.002,T=500 h,Pf≈5.0×10-4,由表4得短路失效的频次为40%,p2d2=2.0×10-4;
由表2得动态开关硅场效应晶体管λP=0.385,T=500 h,Pf≈1.93×10-4,由表4得短路失效的频次为35%,p3d2=1.93×10-4×0.35=6.76×10-5;
环境识别1采用光耦,在其故障模式中没有初级不导通而产生输出电流的故障模式,故pk1k=0;
环境识别2由传感器和模拟电路构成,查表3可得λP=1.538 4,T=500 h,Pf≈7.7×10-4,由表4得控制输出故障模式的频次为40%,pk2k=3.08×10-4;
阻断器由触发器构成,由表3可得单片数字电路失效率λP=0.785 1,T=500 h,Pf≈3.90×10-4,由表4得产生控制输出故障模式的频次为40%,pk3k=1.56×10-4;
逻辑识别控制由MOS微处理器构成,由表3可得λP=2.923,T=500 h,Pf≈0.0014 6,由表4得产生控制输出故障模式的频次为40%,pk4k=0.584×10-4。
2)计算pk1s、pk2s、pk3s、pk4s1、pk4s2
pk1s、pk2s、pk3s、pk4s1、pk4s2和检测端的信噪比有关,即
式中,Ud为检测门限,Ka=4时,pk1s=0.317×10-4,pk2s=0.317×10-4,pk4s1=0.317×10-4,pk4s2=0.317×10-4,pk1d=0.317×10-4,pk2d=0.317×10-4+3.08×10-4=0.34×10-3,pk3d=1.56×10-4+0.317×10-4=1.877×10-4。
代入式(11)可得Pk123d1≈1.139 7×10-9。
代入式(12)可得Pk21≈1.083×10-9。
Ka=3时:pk1s=1.35×10-3,pk2s=1.35×10-3,pk4s1=1.35×10-3,pk4s2=1.35×10-3,pk1d=1.35×10-3,pk2d=1.658×10-3,pk3d=1.506×10-3。
代入式(11)Pk123d1≈0.228 1×10-6。
代入式(12)可得Pk21≈0.224 9×10-6。
3.3 静态开关1正常闭合状态的安全失效率计算
将参数代入式(15)可得
Ka=4时,Pk123d2≈0.340 0×10-4。
Ka=3时,Pk123d2≈0.166 1×10-3。
将参数代入式(16)可得
Ka=4时,Pk31≈0.340 0×10-4。
Ka=3时,Pk31≈0.166 0×10-3。
3.4 两个静态开关均闭合时的安全失效率计算
由式(18)得
Pk123d3≈p3d2+pk4k+pk4T,Pk41=pk4T。
Pk4T通常是软件和硬件错误概率的总和,取0.001 46×0.3=4.38×10-4。
Pk123d3=6.7610-5+0.58410-4+
4.38×10-4=5.6410-4,
Pk41=pk4T=4.38×10-4。
4 三种典型全电子安全系统电路框图安全失效率的讨论
为了叙述方便,称图1所示为全电子安全系统原理框图A。在实际的安全系统设计时,也会采用图9所示的电路框图B。
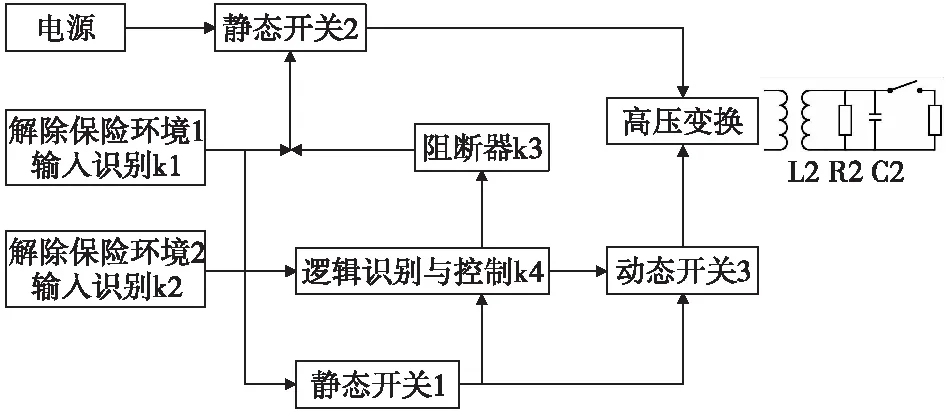
图9 全电子安全系统原理框图BFig.9 The principle B of electronic safety-and-arming system
在引信手册中给出了图10所示的电路框图C。
限于篇幅,我们直接给出忽略高阶小量的三种全电子安全系统的安全失效率计算公式及结果,并将结果列于表5。

图10 全电子安全系统原理框图CFig.10 The principle C of electronic safety-and-arming system

表5 三种全电子安全系统的安全失效率计算公式及结果Tab.5 The formula and result of safetyfailure rate of the 3 kinds of electronic safety-and-arming system

续表
根据表5给出的公式,进行敏感性分析,略去过程,在Ka=4的条件下将各框图对pk1d、pk2d和pk4k的敏感性分析结果列于表6。
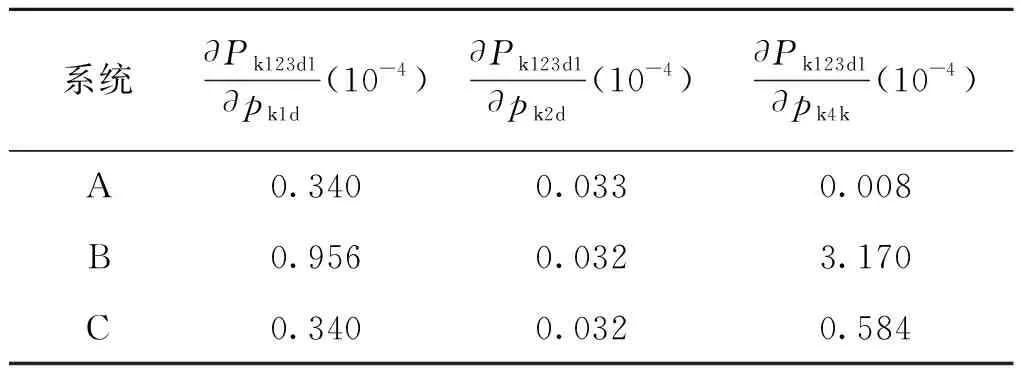
表6 三种全电子安全系统的参数敏感度结果Tab.6 The result ofparameter sensibility of the 3 kinds of electronic safety-and-arming system
由表5、表6可知:
1)系统B的低阶项数多于系统A、系统C,故表中系统B的安全失效风险高于系统A、系统C;除Pk123d1外,系统A、系统C基本相当;
2)解保流程开始前通电状态的Pk123d1:系统B、系统C的值均大于系统A;系统B对逻辑控制器(k4)失效敏感、系统C次之,系统B还对环境识别1(k1)误输出较为敏感;故系统B、系统C通电时三个开关均开启的风险大于系统A;
3)系统C结构对称,正常情况下必须两个逻辑识别控制器均对两个环境都正常识别后,才会启动升压,除Pk123d1外,多数情况下,安全失效率与系统A相当并略低于系统A,但也最易受共因失效的影响。
若逻辑识别控制器k4、k5选用相同器件,
Pk123d1则退化为

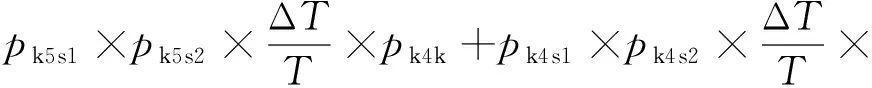
Pk21则退化为
Pk123d2则退化为
Pk31则退化为
计算可知,Ka=3时,Pk123d1由2.42×10-7提升至5.94×10-5时,Pk21由2.24×10-7提升至9.28×10-7;Pk123d2由1.659×10-4提升至3.952×10-4时,Pk31由1.659×10-4提升至3.009×10-4,可见,当存在可信的共因失效时,系统C安全风险很大。
在安全系统详细设计前和安全性审查时,应首先在框图级评估安全失效率并进行敏感性分析,上述分析表明A框图是较为合理的框图。
不论什么形态的安全系统,其安全性的提升均有赖于对检测正确率和时间窗的精度的提高,故解除保险/解除隔离环境信息获取和利用、环境识别器件或组件的低故障率和失效模式控制始终是引信安全控制的关键技术。
5 结论
本文以典型的全电子安全系统为例,给出了非通电状态、通电状态、一个静态开关闭合、两个静态开关闭合下全电子安全系统失效率计算方法。计算了几种典型全电子安全系统的安全失效率,比较了不同框图在不同状态下的安全失效率,说明了在详细设计前如何在框图级评估安全失效率。计算表明:在非通电条件下全电子安全系统比一般机电/机械型安全系统的安全失效率可降低两个数量级;在通电状态下,全电子安全系统的安全失效率取决于解除保险/解除隔离环境识别器件(组件)的故障率水平和环境信息获取和利用的水平,当信噪比为3、时间窗为1/10时,全电子安全系统安全失效率降至和机械/机电安全系统相当的水平。因此,解除保险/解除隔离环境信息获取和利用、环境识别器件或组件的低故障率和失效模式控制始终是引信安全控制的关键技术。
