带有横梁结构的多层目标侵彻过载特征

花俊琦，李 蓉,2，郜王鑫，王志成

(1.西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

现代高科技战争中，为降低大规模杀伤武器的毁伤效能，各个国家不断将重要的军事目标如大规模杀伤武器存储仓库、导弹发射井、指挥中心、飞机掩体等都转移到地下或者深山中。这一类地下工事都是经过钢筋混凝土以及钢板类的建筑材料进行加固并建造多层防护，再加上飞机场跑道、中大型舰船和航母等[1]，为了有效打击此类坚固目标，研制和使用硬目标侵彻弹药这种坚固目标的克星成为了各国军事装备发展的新方向。

侵彻弹命中梁时弹体侵彻过程中受力更为复杂，受到大的侧向力作用，侵彻轨迹偏转，侵彻姿态出现异常。对于引信而言，通过传感器感知到的侵彻过载信号因复杂的侵彻过程呈现出更加粘连的信号[2]。由于梁的厚度导致弹体在上下层楼板间层间自由飞行的距离和时间缩短，弹体中产生的应力波无法快速衰减，信号更加复杂，楼层侵彻过载特征淹没在震荡信号中。

带梁结构是一种常用的建筑结构形式，在实战过程中很难避免对带梁结构的打击，如何有效地摧毁带梁结构目标，是国防领域中结构侵彻研究的重要内容。由于侵彻带梁结构目标撞击过程作用时间短、变形大、接触面复杂以及材料应变率的影响，使撞击过程的理论计算十分困难[3]。以往受试验方法和计算方法的限制，带梁结构的侵彻和穿孔分析均采用将梁系的剖面面积均分到带板上，作为一种相当厚度或相当刚度的板进行简化分析计算，结构材料按线性强化材料处理。随着计算机仿真技术的发展和硬件水平的提高，已经可以按真实的模型进行有限元仿真，以给出物理意义更明确的模型。目前多采用实验与数值模拟相结合的方法，在计算机上进行侵彻实验，其难度、意义都不比传统的试验低，关键在于材料、算法等参数的确定。本文通过不同条件的算例给出侵彻数值仿真的有效方法。

1 典型带梁结构建筑物目标及结构特点

民用建筑、军事建筑都带有横梁结构，横梁结构在建筑物中起到了关键的承重作用。横梁由支座支承，承受的外力以横向力和剪力为主，以弯曲为主要变形的构件。梁承托着建筑物上部构架中的构件及屋面的全部重量，是建筑上部构架中最为重要的部分。且在不同楼层分布的横梁结构不同，作用也不同，大多数梁的方向，都与建筑物的横断面一致。横梁与楼板组成整体的梁-板式楼盖，或与柱组成整体的单层或多层框架。如图1所示，横梁形式多种多样，横梁结构普遍为300 mm×(750～850) mm的尺寸，本文折中选取300 mm×800 mm尺寸。

图1 带梁建筑物结构示意图Fig.1 Schematic diagram of building structure with beams

为了研究带有横梁建筑物多层目标侵彻过载特征，将带梁与不带梁目标侵彻过载特征进行对比，同时建立带梁和不带梁的多层目标侵彻模型，靶板结构尺寸见表1。

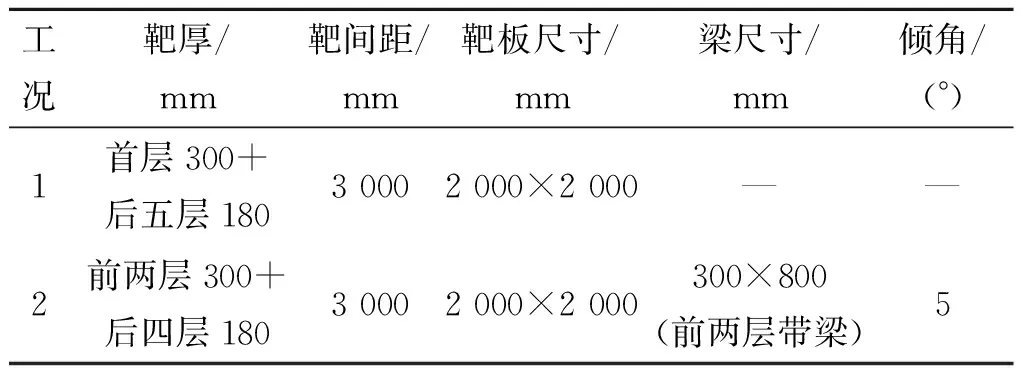
表1 靶板结构尺寸Tab.1 Target plate structure dimensions

2 带横梁结构多层目标建模

为了对比带梁与不带梁的侵彻过载，同时建立带梁和不带梁的多层目标侵彻模型，以考察梁对结构动态响应及塑性区域的影响。利用实测数据验模后进一步开展带有横梁多层目标的侵彻动力学数值计算，计算得到带有横梁结构多层目标的侵彻过载，并对两个过载进行对比分析[4]。

2.1 不带梁和带梁的多层目标侵彻动力学模型

以现役侵彻体为基础，侵彻体重600 kg，直径320 mm，长1 900 mm，着弹点考虑最不利情况位于梁间距中心，混凝土和弹体的单元类型为实体单元Solid 164，算法为单点积分。

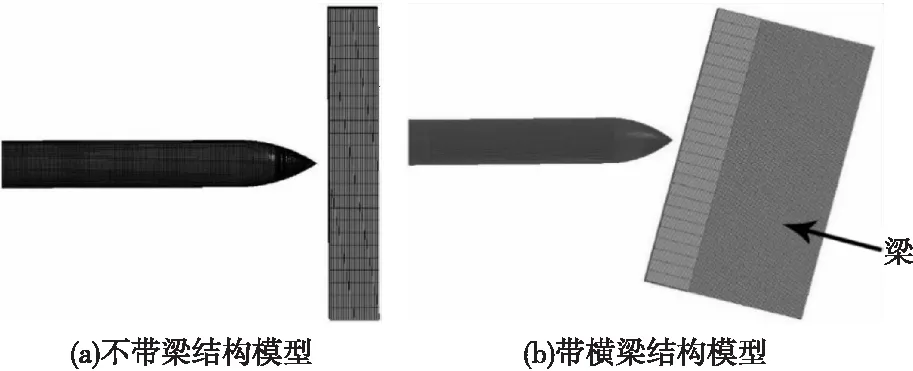
图2 弹靶有限元网格模型Fig.2 Finite element mesh model of bullet target

带梁与不带梁的多层目标侵彻模型采用混合单元法，实现整体宏观模型与局部精细化模型边界条件的直接传递，将宏观模型的一部分附加建立到精细化模型的周边，该部分单元外侧边界节点的相对坐标与宏观模型一致，从而根据节点坐标对应施加整体分析获得的节点力或节点位移，该部分单元内侧边界的低维单元与精细模型的高维度单元之间采用多点约束或基于面约束的接触单元连接，以保证不同尺度模型在界面的变形协调，提高计算效率。

2.2 材料参数及失效准则

LS-DYNA程序中有金属和非金属材料模型近100多种，不仅要考虑应力应变的本构关系从弹性变形到塑性变形，还要考虑材料的损伤和破坏。根据侵彻这一物理过程的特殊性，本文弹体选用*MAT_PLASTIC_KINEMATIC材料，建立与应变率有关的随动硬化或各向同性和随动的混合模型，具体材料参数见表2。应变率用 Cowper-Symonds模型来考虑，屈服应力与应变率关系为

(1)

表2 弹体模型参数设定[5]Tab.2 Parameters setting of the projectile model

式(1)中，σ0为初始的屈服应力；ε为应变率；C，p为

混凝土靶板选用*MAT_JOHNSON_HOLMQUIST_ CONCRETE材料，具体材料参数见表3。H-J-C模型，以材料压缩损伤演化为主，较好地考虑了压缩强度的压力相关性、应变率效应和损伤软化效应，用于预测侵深及弹体的剩余速度较准确。H-J-C模型的强度以规范化等效应力描述为

σ*=[A(1-D)+BP*N](1+Clnε*)。

(2)

表3 混凝土靶板模型参数设定[5]Tab.3 Parameters setting of concrete target plate model

混凝土材料失效通过关键字*MAT _ADD _ EROSION来控制[6]。该模型有压力、主应力、等效应力、主应变、剪切应变、临界应力、应力脉冲失效等7种失效方式。由于冲击荷载作用，混凝土材料强度会随应变率变化，不适合用强度破坏条件。因冲击试验中混凝土主要由受压破坏，所以采用主应变作为混凝土材料失效准则。

2.3 接触-碰撞界面算法

数值仿真程序中处理不同结构界面的接触碰撞和相对滑动是程序非常重要和独特有效的功能，主要有3种算法，即节点约束法(kinematic constraint method)、对称罚函数法(penalty method)和分配参数法(distributed parameter method)。对称罚函数法最常用，其原理比较简单：每一步先检查各从节点是否穿透主表面，没有穿透，对该节点不作任何处理，如果穿透，则在该从节点与被穿透主表面之间引入一较大的界面接触力，其大小与穿透深度、主片刚度成正比，称为罚数值[7]。它的物理意义相当于在从节点和被穿透主表面之间放置一个法向弹簧，以限制从节点对主表面的穿透。同时再对各主节点处理一遍，其算法与从节点一样。对称罚函数法编程简单，很少激起网络沙漏效应，没有噪音，这是由于该算法具有对称性、动量守恒准确，不需要碰撞和释放条件。

整个撞击实验过程的模拟中，各部件之间的接触定义非常重要。面-面自动接触(Contact_Automatic_Surface_To_Surface)用于弹体内部部件之间；面-面侵入接触(Contact_ Eroding_Surface_To_Surface)用于弹体模型与混凝土靶板之间；固-连主从接触(Contact_Tied_Surface_To_Surface)用于弹体与引信和传感器部件之间[8]。

2.4 数值计算结果

当弹体以高速撞击靶板时，弹体穿透靶板的破坏过程见图3，采用H-J-C模型的混凝土靶板在被撞击时能明显地看到被击落的碎屑，效果较好。

靶板的前部和背部破坏模式的数值模拟见图4。数值分析结果表明，靶板被撞击穿透，背部贯穿孔径略大于前部，呈锥形冲切破坏[9]。

图3 弹体侵彻靶板破坏过程Fig.3 Damage process of bullet penetrating target plate

图4 靶板的数值模拟结果Fig.4 Numerical simulation results of the target plate

3 带横梁结构多层目标侵彻过载特征分析

3.1 不带梁多层目标侵彻动力学模型验证

弹体侵彻半无限厚目标的侵彻加速度时间历程曲线遵循图5的规律[10]，图中0～a期间，侵彻阻力不大，加速度也不大，b点所示侵彻阻力接近最大值，且该点加速度值接近最大值，如b～c间所示，之后加速度值维持在最大值附近，随着侵彻深度增加，克服阻力消耗的能量增大，加速度最终降至0，如图5中d点所示。

为了量化的评价侵彻过载的粘连程度，定义层间过载粘连系数p(n)来表示层间过载的粘连程度，具体定义如下：对于过载信号s(t)，若第n层(n>1,n为整数)过载信号峰值对应的峰值时刻为tn，该时刻的过载峰值为s(tn)，则第n-1层与第n层间的层间过载粘连系数p(n)为

(3)

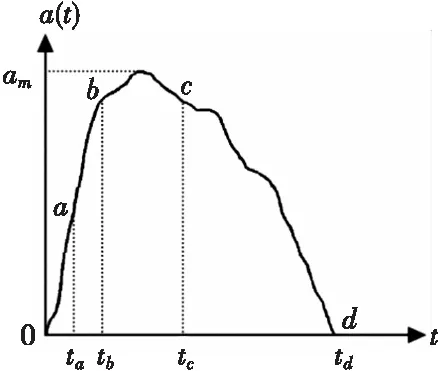
图5 弹体侵彻加速度时间历程曲线Fig.5 Time course curve of projectile penetration acceleration

该系数表示了在第n层过载峰值前(tn-tn-1)/4时间段内过载的均值与第n层过载峰值之比，系数越大，表示层间过载粘连越严重，系数值越小，表示层间过载越清晰。

求得的弹体侵彻不带梁多层目标过载曲线如图6所示，基本符合图5中的侵彻规律。由图6(a)仿真过载可知，侵彻体侵彻6层靶板用时25 ms左右，过载峰值也约为5万g左右。由图6(b)实测数据可知，侵彻体从开始撞击第1层靶板到钻出第6层靶板，历时25 ms左右，过载峰值约为5万g，高速撞击靶板时，由于靶板侵彻阻力，侵彻体受到冲击过载，激发应力波在侵彻体内传播，出现粘连现象[11]。

图6 不带梁多层目标侵彻过载曲线Fig.6 Target intrusion overload curve without beam multilayer

对不带梁结构目标的过载曲线进行特征提取，得到的粘连度，层间持续时间与过载峰值见表4。

表4 不带梁多层目标侵彻过载特征Tab.4 Target intrusion overload characteristics without beam multilayer

对不带梁多层结构目标侵彻仿真的结果与试验数据的进行对比分析，对模拟数值结果和实测数据的过载峰值,层间持续时间和粘连度进行比较，比较结果见表5，图7。

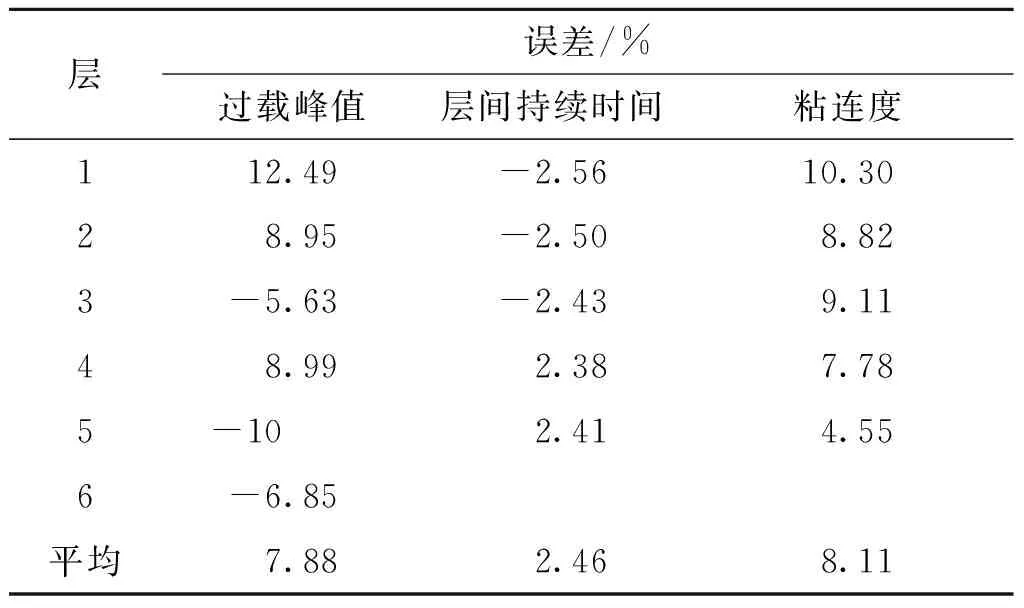
表5 不带梁多层目标侵彻过载与实测过载误差分析Tab.5 Characterisation of intrusion overloads and measured overloads on multi-storey targets without beams

图7 不带梁多层目标侵彻过载与实测过载特征对比结果Fig.7 Results of comparison between intrusion overload and measured overload characteristics for multi-storey targets without beams

以试验数据作为对照，计算仿真数据与试验数据之间的误差，由表5可知，两者的过载峰值最大误差为12.49%，层间持续时间最大误差为-2.56%，粘连度的最大误差为10.30%，且平均误差均小于10%，由此证明侵彻不带梁6层目标模型是可信的。

3.2 带梁多层目标侵彻过载特征分析

数值计算得到的弹体侵彻带梁多层目标过载曲线基本符合图5中的侵彻规律，弹体侵彻6层带梁结构隔靶板的过载曲线如图8所示。在撞靶阶段加速度存在6个明显的波峰，分别对应弹体撞击6层靶板的瞬间，且过载的大小与侵彻速度和靶体厚度有关，前两层带梁靶板最厚，速度也最大，所以在侵彻第一层时加速度相对较大。弹体继续以残余速度侵彻，再次撞击靶板时会再次出现一个过载峰值，加速度振荡是由于应力波在弹体中来回反射导致的。

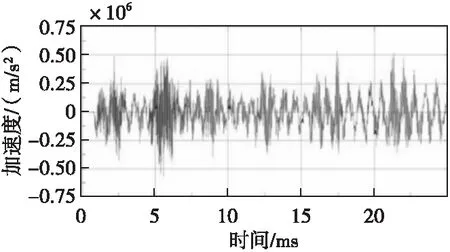
图8 带梁多层目标的侵彻过载曲线Fig.8 Intrusion overload curves for multi-layer targets with beams

对带梁结构目标的过载曲线进行特征提取，得到的粘连度，层间持续时间与过载峰值见表6。

表6 带梁多层目标侵彻过载特征Tab.6 Target intrusion overload characteristics for multi-layer targets with beams

以不带梁结构目标的数据作为对照计算二者误差如表7所示。由表7可知，带梁结构目标的侵彻过载相较于不带梁结构目标的侵彻过载，过载峰值：首层增加了63.67%，第二层增加了36.745，第三层到第六层分别增加了11.91%、7.71%、17.85%、15.27%；层间持续时间：1～2层增加了37.58%，2～3层增加了34.67%，3～6层间分别增加了12.1%、4.7%、5.71%；粘连度：1～2层增加了69.49%，2～3层增加了65.34%，3～6层间分别增加了3.13%、11.36%、16.58%。

表7 带梁多层目标侵彻过载与不带梁多层目标侵彻过载误差分析Tab.7 Characterisation of intrusion overloads on multilayer targets with and without beams

图9 带梁结构与不带梁结构的过载特征对比结果Fig.9 Results of comparison of overload characteristics of structures with and without beams

由图9可知，由于带梁结构的原因，弹体在撞击前两层靶板时过载峰值比不带梁结构目标的过载峰值大，弹体在穿过梁结构之后过载峰值与不带梁结构目标过载峰值一致，且在撞击前两层的过程中，层间持续时间也比不带梁结构目标明显增加，由于过载峰值、层间持续时间的增大，导致带梁结构目标的粘连度比不带梁结构目标的粘连度高。

6 结论

本文建立不带梁和带梁的多层结构目标侵彻动力学模型，在实测数据对不带梁结构目标侵彻动力学模型数值计算结果验模后，在该模型下开展带有横梁结构多层目标的侵彻仿真计算，获得侵彻体侵彻横梁结构多层结构目标的侵彻过载，并对两个过载特征进行过载峰值、层间持续时间和粘连度三项指标的对比分析，得到带有横梁结构多层目标的侵彻过载相较于不带梁结构目标的侵彻过载，首层峰值增加了63.67%、过载持续时间增加了34.95%、粘连度增加了43.18%。研究结果填补了侵彻引信对带有横梁结构多层目标侵彻过载的认识，为侵彻带横梁结构多层目标的准确计层提供了支撑。