低功耗可配置CIC 滤波器设计
2023-03-07高敏于宗光万书芹邵杰
高敏 ,于宗光 ,万书芹,邵杰
(1.江南大学 物联网工程学院,江苏 无锡 214122;2.中国电子科技集团公司第五十八研究所,江苏 无锡 214035)
级联积分梳状(Cascade Integral Comb,CIC)滤波器只包含加法器和寄存器,因具有设计实现简单、运行速度快并且所需资源少等特点[1],作为常用模块应用于数字下变频(DDC)和数字上变频(DUC)系统中[2-3]。伴随集成电路的高速发展,传统型CIC 滤波器结构已经不能满足工程需求,设计低功耗可配置的CIC 滤波器结构成为当前产业的发展趋势。
梅海军等[4]提出采用非递归滤波结构以降低CIC滤波器的整体功耗,但额外引入滤波系数且采样因子固定(2 的整数倍),难以适应多样需求。高维等[5~6]引入非递归多相分解结构,虽有效降低功耗,但难以复用同一电路以实现不同的抽取倍数。为克服非递归形式的缺陷,王尧等[7]采用递归滤波结构,实现多抽取率的CIC 滤波器,但功耗和面积过高。为改善性能,王璞等[8]采用Hogenauer 剪除算法,减小内部寄存器位宽,能在一定程度上降低功耗并减小面积,但是数据转换精度不够高。
为降低功耗和设计面积,并满足多种输入信号带宽下对转换精度的要求,本文提出一种基于半字节串行算法的可配置CIC 滤波器,通过优化内部位宽,并在不同采样因子下复用逻辑电路,可降低系统功耗和提高资源使用率。信道带宽配置模块提供2~16 倍范围内的可编程采样因子,以实现带宽可变功能。增益校正模块优化末级输出有效精度并减小信号失真。为减少硬件资源开销,采用正则有符号数(Canonic Signed Digit,CSD)编码表示法对系数进行编码,并利用移位替代乘法运算,最终基于65 nm COMS 标准单元工艺库完成DC 综合,结果表明所设计的数字滤波器在低功耗方面具有较大优势。
1 基本原理
1.1 CIC 滤波器
1.1.1 单级CIC 滤波器
单级CIC 滤波器是一种FIR 滤波器,具有线性相位特性[9],主要由积分器和梳状滤波器级联构成。根据级联顺序的不同,可构成CIC 插值和抽取滤波器[10],分别如图1(a)和(b)所示。其中,D为抽取/插值因子,M为延迟因子。
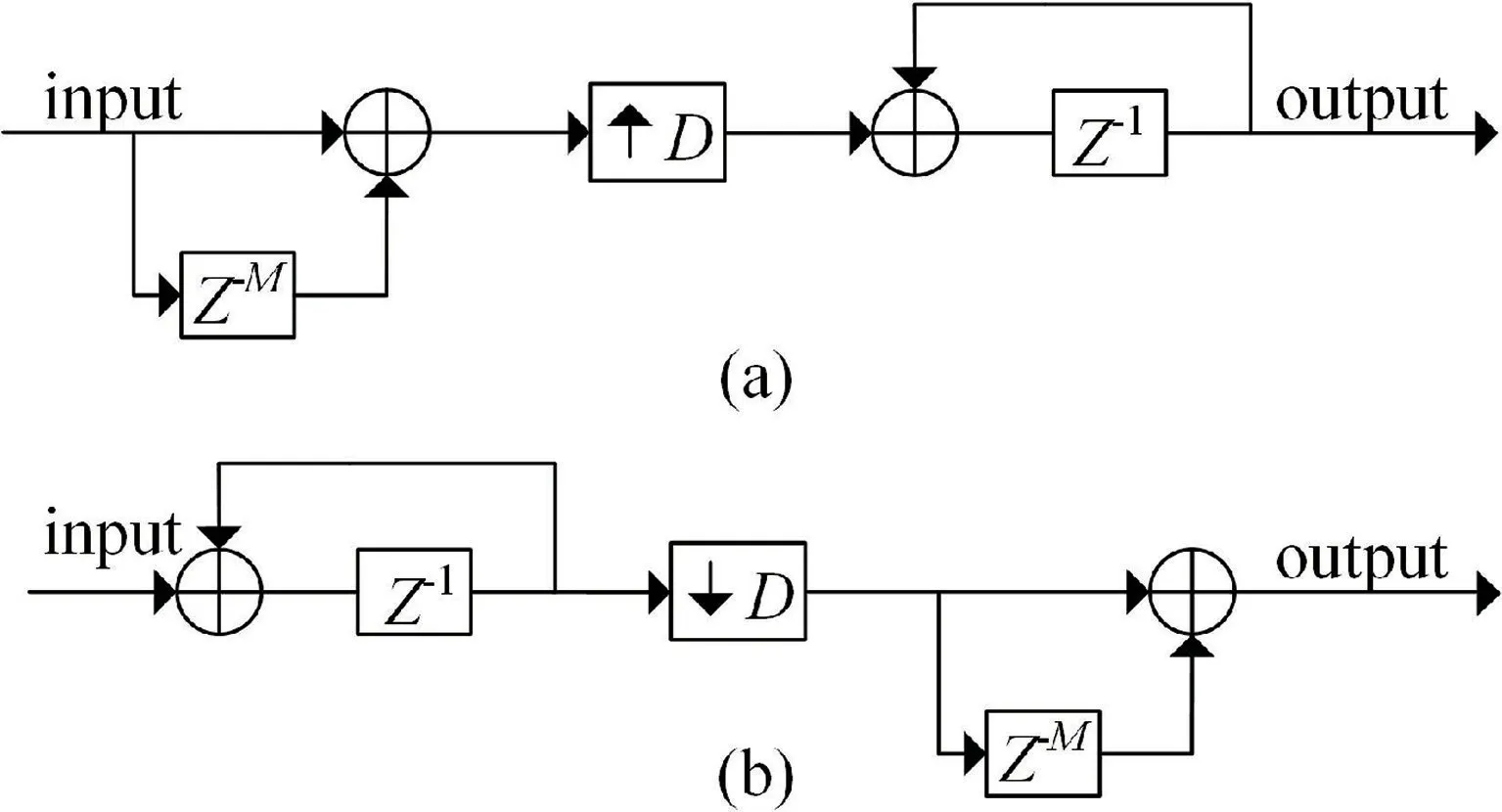
图1 单级CIC 滤波器结构。(a) CIC 插值滤波器结构;(b) CIC 抽取滤波器结构Fig.1 The structure of single-stage CIC filter.(a) The structure of CIC interpolation filter;(b) The structure of CIC decimation filter
CIC 滤波器的传递函数为:
将z=ejω代入式(1),可得单级CIC 滤波器的幅频响应为:
式中:Sa(x)=为抽样函数,Sa(0)=1,则CIC 滤波器在ω等于0 时幅度值为DM。图2 展示了单级CIC滤波器的频率特性。阻带衰减较严重,约为13.46 dB,旁瓣电平较高,容易出现混叠现象。
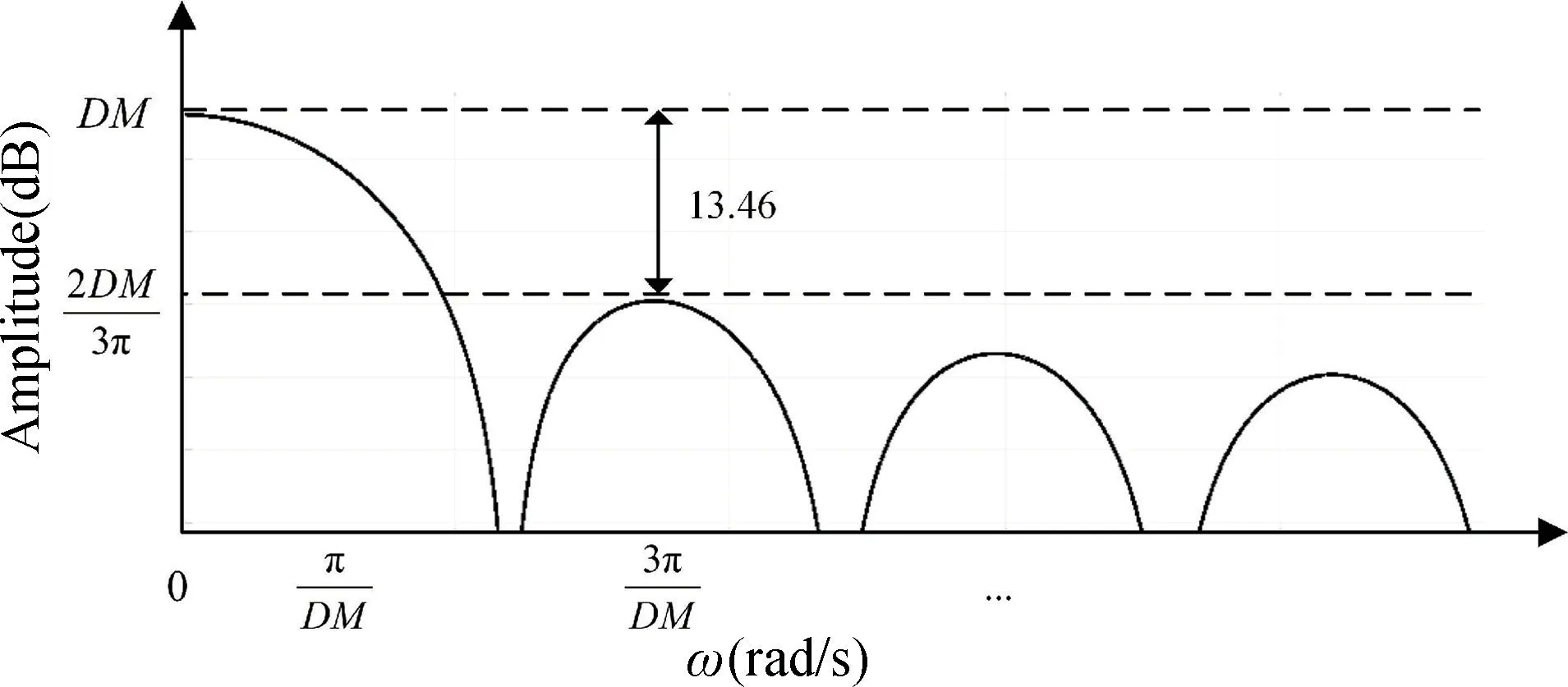
图2 幅频响应特性曲线Fig.2 Amplitude frequency response characteristic curve
1.1.2 多级CIC 滤波器
多级级联CIC 滤波器可改善单级CIC 滤波器的缺陷,其通过降低旁瓣电平提高阻带衰减。多级CIC 滤波器的阻带衰减为[11]:
式中:N为级联数,伴随N值增大,阻带和通带衰减增加,导致通带平坦度降低,因此N不宜过大[12]。
1.2 优化设计原理
以降低系统功耗和减小设计面积为目标,本设计提出的滤波器结构可有效改善功耗和面积问题。采用半字节串行算法技术,可有效减小寄存器内部位宽。为适应不同带宽需求,提供可编程的采样因子,同时对输入信号字长进行有效扩展,使采样因子大小不同时仍可复用同一电路。配置增益校正模块以减小信号失真,并采用CSD 编码方式对增益校正模块中的乘法系数进行编码,以有效减小乘法器面积。
1.2.1 位宽扩展
当采样因子D和滤波器阶数N过大时,由于积分器模块不断进行累加操作,运算数据则需要更大字长的寄存器进行存储,但内部寄存器位宽是有限的,因此递归型级联CIC 滤波器的输出数据产生溢出,导致输出信号严重失真。若数据流采用二进制补码形式,并且累加器和寄存器的位宽足够大时,则滤波器能正确输出信号。
寄存器最大位宽由直流增益决定[13],当频率趋近于0 时,增益G如式(4)所示:
为了避免溢出,寄存器的实际位宽应依据式(5)计算得出[14]:
式中:Bmax为CIC 滤波器各级存储器最大有效字长;Bin为输入位宽;Nlog2(DM)取值遵循向上取整规则。为了便于采用多路复用技术以减少资源开销,D的取值设置为采样因子可调范围内的最大值。
1.2.2 半字节串行算法
采用半字节串行算法[15]可将输入信号从最低有效位MSB 至最高有效位LSB 依次拆分为多位字长相同的信号输出,输出数据串行交叉或者多路复用在高速通道中。为有效优化内部寄存器位宽并节省逻辑单元数,利用该算法将输入的每个数字中频信号从LSB 至MSB 拆分为4 个位宽一致的信号,依次从低位到高位串行输出。
1.2.3 可编程因子
在数字上/下变频系统中,为实现带宽可变功能,CIC 滤波器的采样因子应可编程或可配置。数据的下采样过程即通过跨时钟域将高频信号分量输出为低频信号分量,上采样过程则相反。
对于采样因子固定的CIC 滤波器,为实现抽取运算需要根据相应的采样因子在连续信号间隔D个周期输出数据,而实现插值运算则需在每个时钟周期内插入D-1 个零值。因此,为实现可配置的CIC 滤波器,主时钟根据可调的采样因子生成相应的分频时钟,对数据进行采样处理,即可完成相应的抽取和插值功能。
1.2.4 增益校正
积分器中连续的累加运算不可避免产生溢出,导致输出比特增长,引起滤波器输入输出之间的滤波增益升高。为了减小信号失真,同时节约后级大量硬件资源[16],在设计中配置增益校正模块使末级输出数据的精度有限。
增益校正模块分为截位模块和常系数乘法器。若增益G的表达式(4)中DM的乘积为2 的幂指数的形式,即G=(DM)N=2KN,则直接裁剪输出数据的低KN位,保留与输出位宽长度相同的高位部分。当DM的乘积不为2 的幂指数的形式时,若直接将输出结果乘上增益因子G的倒数,则会造成乘法器位宽和设计面积过大。
为进一步优化设计面积,提高资源利用率,本设计针对传统增益校正模块的不足之处进行优化。即当增益值G不为2 的整数次幂时,将增益表达式转换为如下形式:
式中:X为2 的整数次幂所表示的数,且这个数最接近于DM,则直接对输出进行右移以实现这部分乘积的增益校正;剩下的乘积部分(DM/X)N,首先对该乘积倒数进行量化,其中量化位宽为A,后采用CSD 编码方式对量化后的数进行编码,最终通过移位、加减法运算和截位实现增益校正。综上,通过将截位后的信号与乘法系数相乘,并舍弃掉低A位乘法运算结果,保留所需高位数据,以此实现增益校正。
1.2.5 CSD 编码
增益校正模块中的常系数乘法器需要存储一定量的配置系数,为减小乘法器面积,使用CSD 编码方式对乘法器系数进行优化,可降低系数中非0 元素数量。
CSD 编码方式如下[17]:
从上述CSD 码的编码方式总结得出: 任何相邻的两位中,必包含1 个0,故CSD 表示法中非0 元素的数量不会超过系数位宽总数的一半。所以利用CSD 编码表示法对乘法器系数进行编码,可获得更多0 位,进而优化乘法器的面积。
2 MATLAB 建模
2.1 总体模型
采用MATLAB Simulink 搭建CIC 滤波器模型,以验证半字节串行算法的可行性。由于CIC 抽取滤波器和内插滤波器的实现上,只是数据流的方向不同,而方法一致,见本文第1 部分基本原理说明,在此仅对抽取类型的滤波器进行详细设计。
经对音频领域应用需求进行分析,需要设计一个能够实现2~16 倍抽取频变因子、通带带宽为15 kHz~4 MHz、阻带衰减大于50 dB 且输入/输出位宽为22 比特的抽取滤波器,综合考虑确定该CIC 滤波器的级联参数N和延迟因子M分别取值为4 和1。基于本文提出的CIC 实现结构,设计了一款通用的CIC 抽取滤波器。
CIC 抽取滤波器整体模型如图3 所示。采用转换器Conversion 将输入信号有效位宽拓展至40 比特,后利用片选器Bit Slice 将输入数据依次从MSB 至LSB切分为4 组10 比特数据串行输出。四级级联积分器做累加运算,抽取器对末级积分器输出数据进行降采样处理,每间隔64 个时钟周期,利用(4 个步长分别相差1)Downsample 模块进行一次下采样,多路选择器Multiport Switch 将4 路并行采样结果转化为1 路串行数据输出。梳状滤波器comb 模块对数据进行滤波处理,并将滤波后的数据分为4 路并行数据(分别相差一个时钟周期)同时传输给Bit Concat 模块,该模块将数据从MSB 至LSB 拼接为位宽40 比特的数据传输给片选器,对数据做截位处理,最终实现CIC 抽取滤波器降采样和滤波功能。

图3 CIC 抽取滤波器模型Fig.3 The model of CIC decimation filter
2.2 功能验证
基于半字节串行算法的CIC 抽取滤波器仿真波形如图4 所示,正确实现16 倍下采样功能,输出所需低频分量。
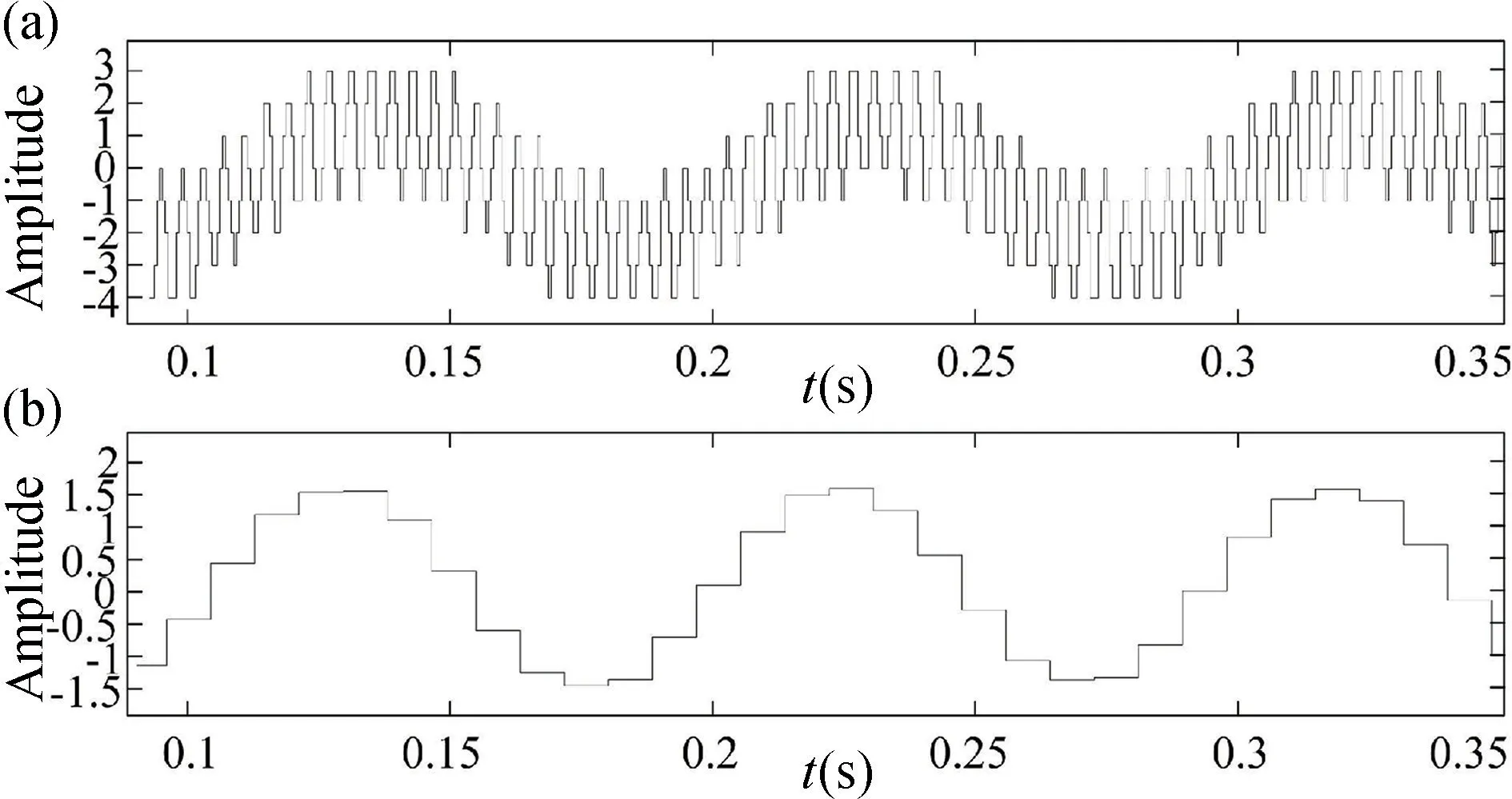
图4 D=16 时的仿真波形。(a) 输入波形;(b) 输出波形Fig.4 Simulation waveform when D=16.(a) The waveform of input;(b)The waveform of output
输出信号频谱如图5 所示,CIC 抽取滤波器滤除高频信号,留下低频信号。结果表明搭建的模型功能正确,完成了降采样和滤除高频噪声的功能。

图5 输出信号频谱Fig.5 The spectrogram of output signal
3 ASIC 电路设计
3.1 系统设计
根据MATLAB 建模设计原理进行ASIC 电路设计,本设计的整体架构包括信道带宽配置模块、时钟控制模块和CIC 抽取滤波器实现模块,如图6 所示。时钟控制模块通过信道带宽配置模块提供的下采样因子D产生各模块所需的低频时钟或使能信号。CIC 抽取滤波器编码模块将输入数据一分为四串行输出给积分器做累加处理,抽取器对累加处理后的数据进行D倍下采样后传输给梳状滤波器完成滤波处理,由位拼接模块将拆分后的数据重新组合为完整数据,最后经由增益校正模块调整输出精度。

图6 总体结构框图Fig.6 The block diagram of overall structure
3.2 编码模块设计
首先,为保证精度以及避免数据溢出,根据位宽扩展公式(5)确定最大扩展位宽为40 比特,拓宽的有效位由输入数据的最高有效位填补。随后基于半字节算法原理,将拓展位宽后的信号依次从MSB 至LSB 切分为4个位宽10 比特的数据从低位至高位串行输出。
3.3 积分器和梳状滤波器设计
积分器主要由加法器和寄存器构成,在不影响输入流的情况下,每4 个串行数据累加完成后开始新一轮累加。其状态方程为:
积分器结构如图7 所示,积分器输入数据为编码数据,有效位相加产生进位,产生的进位信号存储在寄存器中,并延时一个时钟周期后向高位进位。4 个串行数据完成累加后,相当于40 比特数据运算完成,故最后一次累加产生的进位信号不参与下一次累加运算。

图7 积分器结构Fig.7 The structure of integrator
梳状滤波器同样主要由加法器和寄存器构成,每4 个串行数据加法运算完成之后加法器清零。其状态方程为:
梳状滤波器结构如图8 所示,采用数据直接取反的方式将减法运算转化为加法运算,简化了运算器的电路结构。
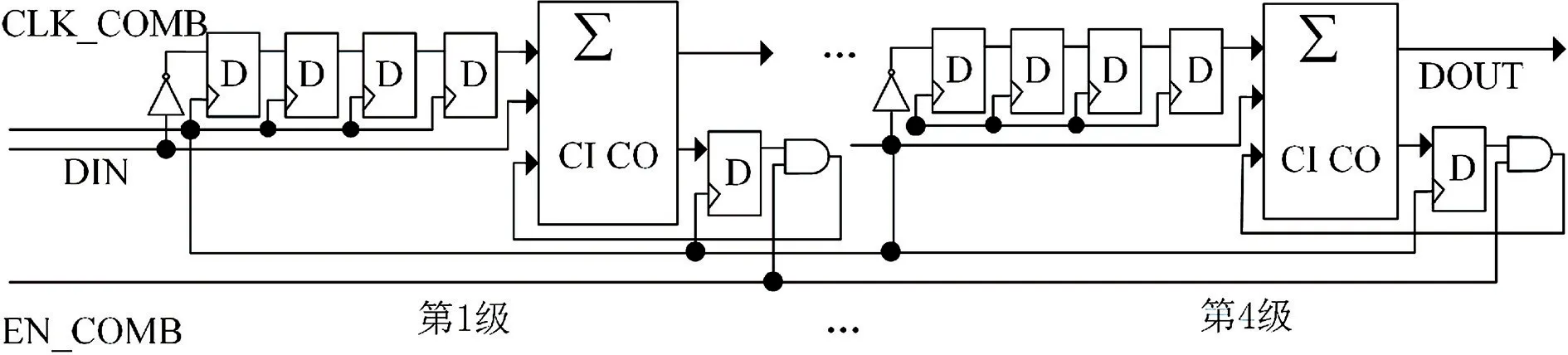
图8 梳状滤波器结构Fig.8 The structure of comb filter
3.4 抽取器和增益校正模块设计
3.4.1 抽取器设计
抽取器将级联积分器末级输出的4 路数据x(n)、x(n-1)、x(n-2)和x(n-3)分别进行D倍下采样,并对4 路采样数据进行串并转换以获得1 路输出数据。
3.4.2 增益校正模块设计
当增益值G为2 的整数次幂时,采用右移运算完成增益校正。反之则根据式(6)先对输出信号完成相应的截位运算,后对上述运算的结果进行右移运算和加/减法运算,以便实现乘以相应系数的功能。此外,利用CSD 编码乘法系数替代全位宽二进制补码编码乘法系数。其中乘法系数被量化为16 位有符号数。最终,依据0 舍1 入的进位法则,舍弃乘法运算结果的低16 位,同时为满足输出信号位宽要求,保留所需高位数据。
4 验证与综合
4.1 仿真验证
基于Verilog HDL 语言,采用自顶向下的层次化设计思路,完成采样因子为2~16 倍的CIC 滤波器的RTL 级描述,并搭建VCS 仿真器环境进行功能验证。
其中,输入信号为50 MHz 和1 MHz 的正弦波混合信号数据,以抽取率D=2 为例,输出仿真波形如图9 所示,结果表明所设计的CIC 抽取滤波器功能正确,不仅滤除了50 MHz 高频噪声分量,还实现了2 倍抽取功能。
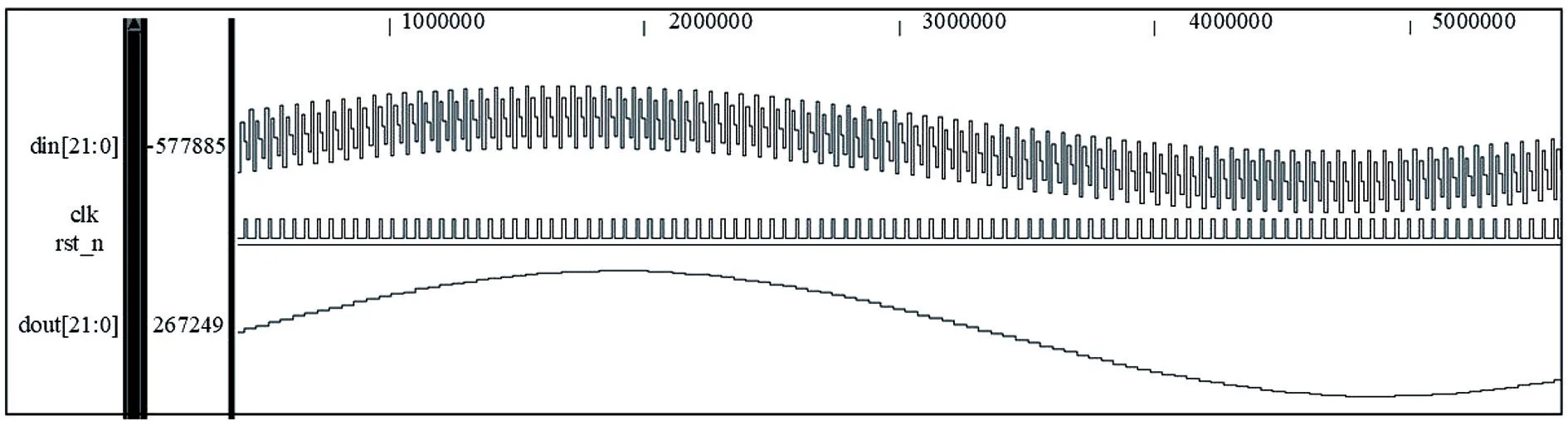
图9 输出仿真波形Fig.9 The simulation waveform of output
4.2 DC 综合
采用Synopsys 公司的Design Compile 综合工具,基于65 nm COMS 标准单元工艺库对ASIC 电路进行综合,得到相应的门级网表,如图10 所示。

图10 CIC 滤波器DC 综合网表Fig.10 The DC synthesis netlist of CIC filter
抽取倍数灵活的CIC 滤波器大多采用递归型结构。王尧等[7]实现具有16,32,64 和128 倍抽取功能的CIC 滤波器,由于内部寄存器位宽过大,使得功耗和面积过高。为对比上述设计思路,采用结合传统算法和二进制补码乘法[7]以及结合半字节串行算法和CSD 码乘法(本文)两种方法分别设计能够实现2~16倍抽取功能的CIC 抽取滤波器,并进行DC 综合。本文提出的结构和传统结构所设计的滤波器性能参数对比如表1 所示。结果表明,本文设计的滤波器在功耗和面积方面具有优势,特别是在抽取倍数和数据位宽过大时,这种优势将会表现得更加明显。

表1 性能参数对比Tab.1 Comparison of performance parameters
5 滤波器实现与仿真分析
5.1 布局布线
布局布线(Placement and Routing)就是将前端逻辑综合产生的门级网表、约束文件和库文件等通过电子设计自动化(Innovus)软件转换为版图,图11 为CIC滤波器设计版图。

图11 CIC 抽取滤波器的设计版图Fig.11 The layout of CIC decimation filter
5.2 门级仿真
为模拟实际电路的运行效果,需要将版图设计产生的延时信息、寄生电容和电阻添加到后仿真中,即门级仿真。
如图12 所示,展示了抽取倍数为4 的门级仿真波形。结果表明,本设计正确地实现4 倍下采样和滤波功能,同时满足时序和信号完整性要求。

图12 CIC 抽取滤波器门级仿真波形Fig.12 The gate-level simulation waveform of CIC decimation filter
5.3 工程应用
基于本设计方案,设计级联数N=4,延迟因子M=1,抽取因子D为2~16 倍的CIC 滤波器。此外,CIC 滤波器级联3 级半带滤波器,综上可实现抽取因子为16~128 范围内的数字滤波器,其ASIC 电路已应用于某数字接收机工程设计中。基于65 nm CMOS 工艺对本文的CIC 抽取滤波器进行版图设计,如图13 所示,白色框内的即为数字电路版图。

图13 数字电路整体版图Fig.13 The overall layout of digital circuit
经测试,输入信号频率为2.385 MHz,经过混频模块及数字滤波器下采样得到频率为135 kHz 的基带信号,信号频谱幅度为85 dB,如图14 所示。
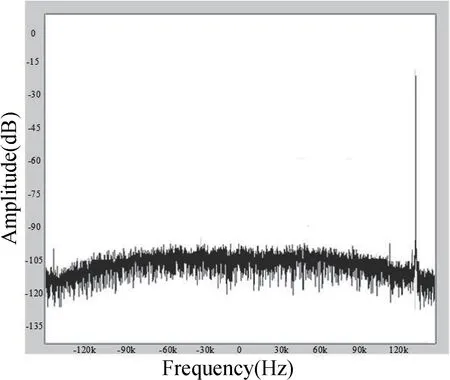
图14 数字电路测试结果图Fig.14 The test result graph of digital circuit
6 结论
本文设计了一种基于半字节串行算法的低功耗可配置级联CIC 抽取滤波器。为减小功耗,对传统CIC滤波器结构进行改进和优化。采用半字节串行算法及多路复用技术,减少内部运算和存储单元使用。提供可编程采样因子,能够灵活处理多速率信号,适用于多种信道带宽并存的通信系统。为进一步降低功耗,采用CSD 编码替代传统二进制补码编码方式,大幅减少逻辑资源的消耗,最终实现了低功耗可编程的CIC滤波器。
