脉冲用金属化膜电容器稳态热分析研究
2023-03-07邱昊高秀华邱林俊王勇平
邱昊,高秀华,邱林俊,王勇平
(成都宏明电子股份有限公司,四川 成都 610000)
金属化膜是利用高真空蒸镀技术,在有机薄膜(如聚丙烯、聚酯等)表面蒸镀一层铝、锌和锌铝复合金属薄层而成,其特点是金属层厚度薄。以厚度为纳米级的导电金属层作为电容器电极,为电容器小型化提供新的思路。金属化膜电容器具有储能密度高、可靠性高、寿命长和损耗小等特点,是脉冲功率系统中常用的储能元器件,常用于微波、激光、粒子加速器、电磁武器、医疗器械、勘探和环保领域等。
目前脉冲用金属化膜电容器一般采用聚丙烯薄膜作为介质,蒸镀电极材料为锌铝复合材料。由于金属电极很薄,金属化膜方阻较大,在连续长期工作下电容器发热是一个重要问题,会导致电容器工作失效,甚至燃烧、爆炸等故障。
李化等[1]提出在金属化膜电容器温升模型中,等效串联电阻(ESR)在脉冲放电结束后产生热量由金属电极向有机薄膜径向传导,并且轴向往端面传导;范丽娜等[2]提出电容器外表温度和电容器芯子最热点的关系,对预测电容器使用寿命非常有价值;徐梦蕾等[2]提出膜块宽度与熔丝宽度比、环境温度对电容器最高温度的影响,推导出各影响因素与最高温度的对应关系。
因此,从脉冲用电容器运行稳定性、金属化膜耐压性能和电容器寿命等方面考虑,有必要对电容器稳态运行进行热分析,开展电容器散热优化设计。本文采用有限元仿真软件,依据电容器零部件尺寸和装配条件建立模型,通过仿真计算结果和试验结果对比,验证了仿真模型的准确性。最后,通过芯子卷绕参数和电容器工作周期理论计算,进行电容器优化设计,降低了电容器稳态运行内部温度,提高了电容器运行的稳定性和安全性。
1 金属化膜电容器发热理论
金属化膜电容器主要发热源有: (1)有机薄膜介质损耗发热;(2)金属电极发热;(3)端面接触不良发热[4-7]。李智威等[8]提出金属化膜电容器在脉冲工作模式下,高方阻金属电极发热大于薄膜的介质损耗发热,额定工况下电容器端面接触发热可以忽略不计,电极电阻发热是主要的发热来源。
1.1 等效电阻计算
在额定工况下,金属电极总发热功率近似等于电容器极板损耗功率[9]。
式中:Im为电流有效值;ESR 为电容器等效串联电阻。金属化膜结构见图1。电容器容量C为28 μF。

图1 金属化膜结构图Fig.1 Structure diagram of metallized film
由P=P损耗,可得:
式中:L为极板有效长度;b为有效宽度: 90 mm;Δb为卷绕留边: 4 mm;Δb'为卷绕错边: 1 mm;为金属化膜方阻: 160 Ω;r'为电容器接触电阻和电极电阻。通过式(2) 计算可得等效串联电阻ESR 为0.16 Ω。
1.2 电容器工作周期
一般脉冲功率系统按工作方式可分为两类: 一是连续工作模式,以重复频率长时间持续工作;二是爆发工作模式,以重复频率连续工作时间t1后,间隔时间ti,按照t1+Tr规律长时间工作。脉冲功率系统重复频率工作时,电容器、开关等关键器件温升较大。单次电容器工作周期可分为: 充电阶段、保压阶段、放电阶段和间隔阶段[8]。
电容器工作周期见图2。其中,tc: 充电阶段时间,th: 保压阶段时间,td: 放电阶段时间,ti: 间隔时间,Tr: 电容器工作周期。
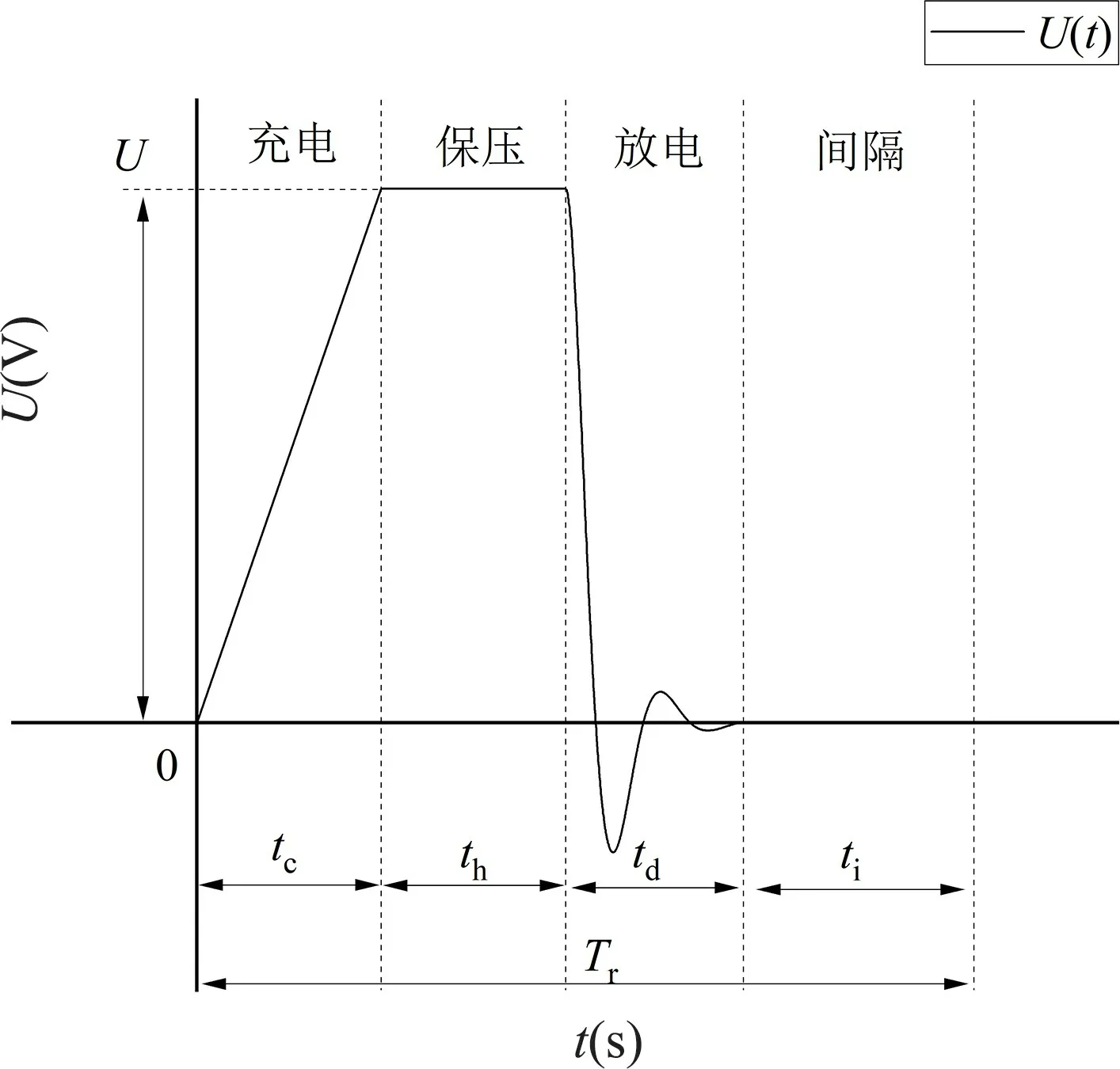
图2 电容器工作周期Fig.2 Working period of capacitor
1.3 发热功率计算
电容器长期运行,通过讨论其高重复频率工作的发热功率为电容器热分析提供依据。电容器典型放电回路见图3。其中,电容器杂散电感ESL: 0.2 nH,负载R: 2.4 Ω。
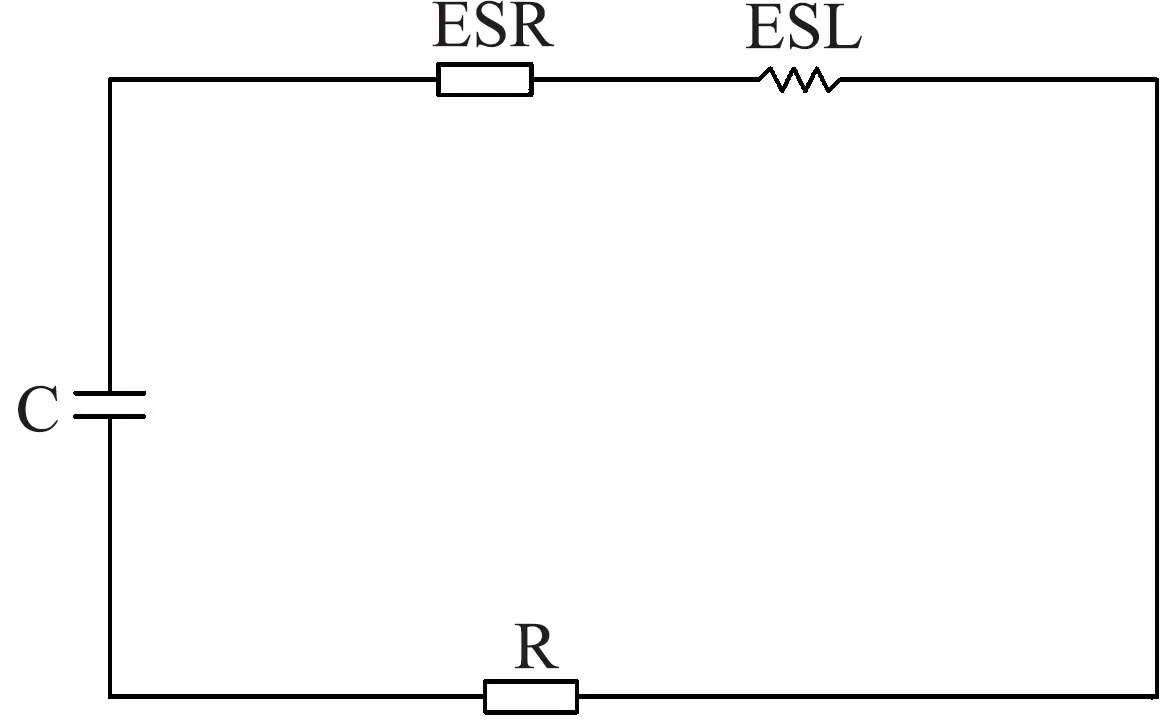
图3 电容器典型放电回路图Fig.3 Typical discharge circuit of capacitor diagram
单次脉冲金属化电容器充放电回路总功率为:
单次脉冲金属化膜电容器发热功率为:
2 金属化膜热传导理论
依靠构成物质的粒子,如原子、分子、自由电子,从物体较热区域向较冷区域提供的能量称为热。热传导是一种特定方式的传热,这种传热方式的能量交换发生在固定或静止流体内,依靠物体内部的温度梯度从高温区域向低温区域传输能量[11]。
2.1 金属化膜电容器热传导过程
金属化膜电容器由金属化膜卷绕而成,每层金属电极都会发热向相邻有机薄膜传导。在仿真计算中,将卷绕的电容器芯子看成均一的介质[12]。金属化膜电容器热传导过程见图4。
图4 电容器热传导过程图Fig.4 Heat conduction process diagram of capacitor
2.2 金属化膜电容器芯子各向异性
在各向同性的固体中的热传导,各向同性材料的导热系数与方向无关,所以导热系数无需考虑方向问题。由于金属化膜是在有机薄膜表面真空蒸镀一层金属电极复合材料,因此研究金属化膜电容器内部热传导需要考虑金属化膜材料的各向异性。金属化锌铝膜最大优点是容量损失小、抗氧化性强、镀层与有机薄膜附着力强[14]。电容器在工作过程中,自愈面积与自愈持续时间随着自愈能量的增加而增加,自愈能量与电压二次方成正比、与方阻的二次方成反比,采用高方阻金属化膜可有效降低容量损失,提高电容器寿命[15]。因此脉冲用电容器一般采用锌铝复合高方阻金属化膜。金属化膜电容器芯子展开图见图5。
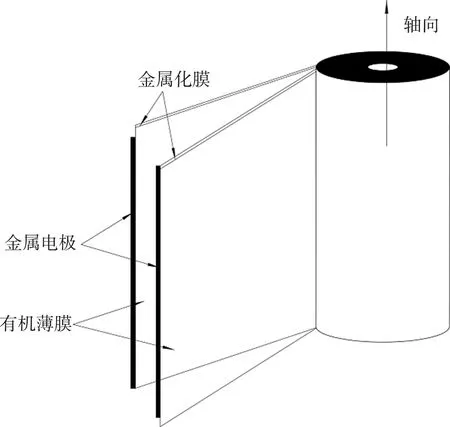
图5 金属化膜电容器芯子展开图Fig.5 Expanded diagram of the core of metallized film capacitor
在电容器内部,热量沿电容器芯子轴向和径向进行热传导。沿轴向等效热导率为:
式中:dm为金属电极厚度;dp为有机薄膜厚度;λm为金属导热系数;λp为有机薄膜导热系数。
当热量沿芯子径向传导时,则径向等效热导率为:
金属化膜电容器芯子传热微元见图6。通过式(5)和式(6)计算可得芯子在三维坐标系下各向异性导热系数。X,Y,Z轴导热系数分别为: 0.22,0.22,0.226 ℃/W。
图6 芯子传热微元Fig.6 Heat conduction micro element of core
2.3 金属化膜电容器散热
电容器散热方式主要有对流散热、辐射散热和传导散热[14]。处于无限大空间中时电容器各个表面对环境的散热表现为自然对流散热。电容器在空气自然对流散热计算公式见式(7)。
式中:λ为空气导热系数;L为传热面特征长度;Nu为Nusselt 数。本文研究的是在无限大空间中,恒热流电容器进行自然对流散热。对流散热系数一般与物体形状、环境特性等因素有关。
对于恒热流竖直平壁散热表面Nusselt 数为:
对于恒热流水平散热表面,分热面向上(冷面向下)和热面向下(冷面向上),对应Nusselt 数为:
式中:Gr为Grashof 系数,表示流体的浮生力和粘性力的相对大小;Pr为空气普朗特数。格鲁晓夫Gr计算公式为:
式中:αv为空气膨胀系数;Tw为物体表面温度;T0为环境温度;g为重力加速度;v为运动粘度。
假设空气为理想气体,空气膨胀系数为:
本文综合散热系数h通过式(7)计算可知为6.8 W/(m· ℃),其中Pr、v和λ可以通过文献[14]查询。
3 金属化膜电容器理论模型与仿真
有限元法(Finite Element Method)是一种将连续体视为若干个有限大小的单元体的离散化集合,以求解连续体热、力、电磁问题的数值方法,其基本思想是将连续的求解区域离散为一组有限个、且按一定方式相互连接在一起的单元的组合体[15]。
3.1 模型搭建
利用SolidWorks 软件对金属化膜电容器按照零部件尺寸和装配条件进行建模。电容器模型包含: 芯子、喷金层、环氧树脂、引出电极和PPS 外壳[16]。根据电容器结构特点和本文研究内容对电容器仿真模型作以下简化和假设:
(1)由于电容器内部结构复杂,忽略引出电极和焊点的影响,电容器芯子作为均匀发热源;
(2)将电容器内部有机薄膜及锌铝金属层等效为一种材质,考虑在三维坐标系下电容器芯子沿其轴向和径向热传导;
(3)忽略电容器芯子内部空间间隙;
(4)电容器芯子端面施加喷金层,电容器内部除零部件之外全部填充环氧树脂。
3.2 建模结果分析
在SolidWorks 中建立金属化膜电容器三维仿真模型,电容器由内到外包含: 1 根芯棒,1 个芯子,芯子与外壳之间填充聚氨酯,1 个外壳。电容器仿真模型见图7。
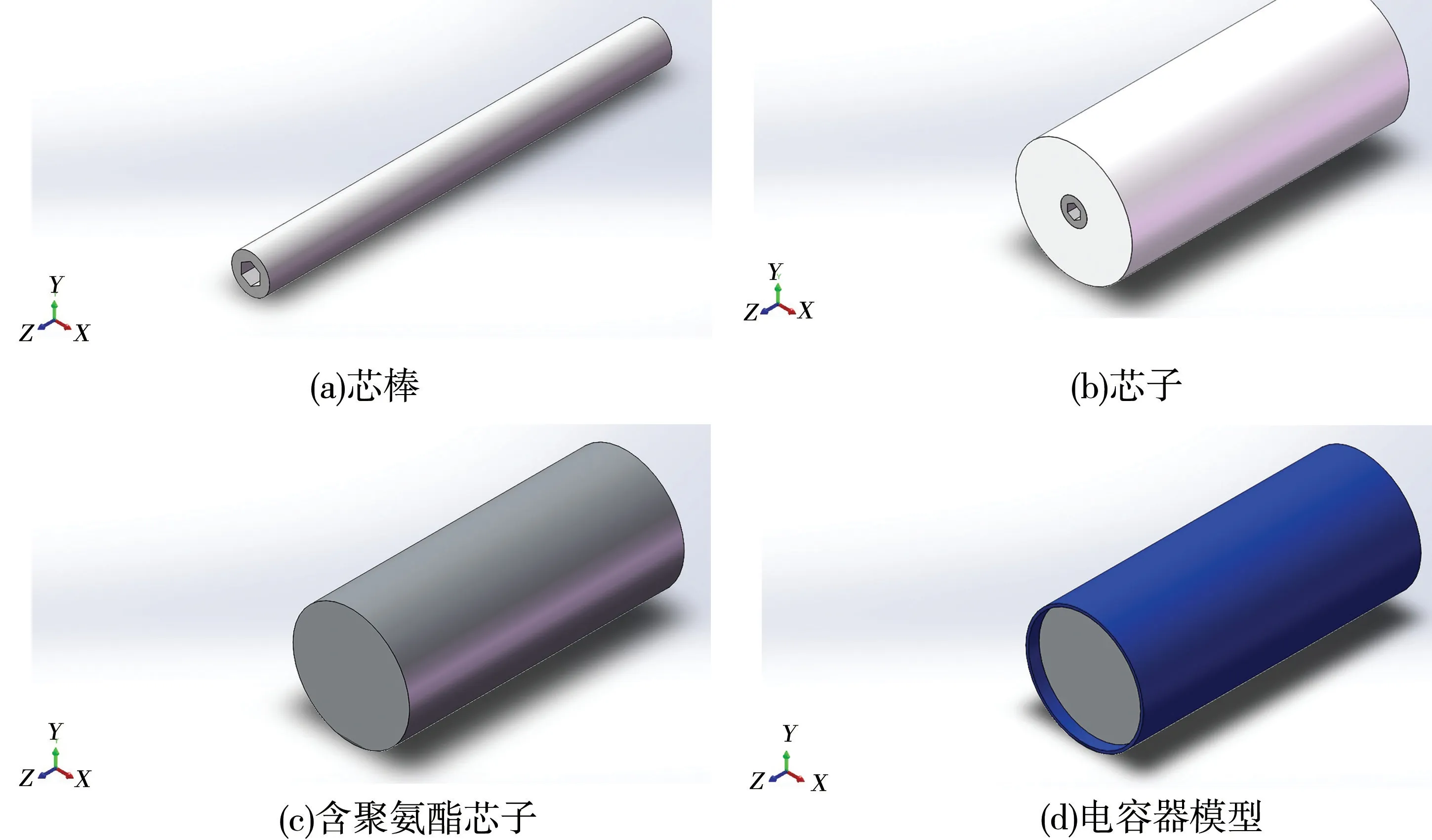
图7 电容器仿真模型Fig.7 The simulation model of capacitor
3.3 材料属性定义
利用SolidWorks 软件对电容器进行稳态热分析时,需要对材料的导热系数、比热容和质量密度进行定义。芯子各向异性的导热系数已知,其余材料通过查阅资料得到电容器材料属性参数见表1 所示[14]。
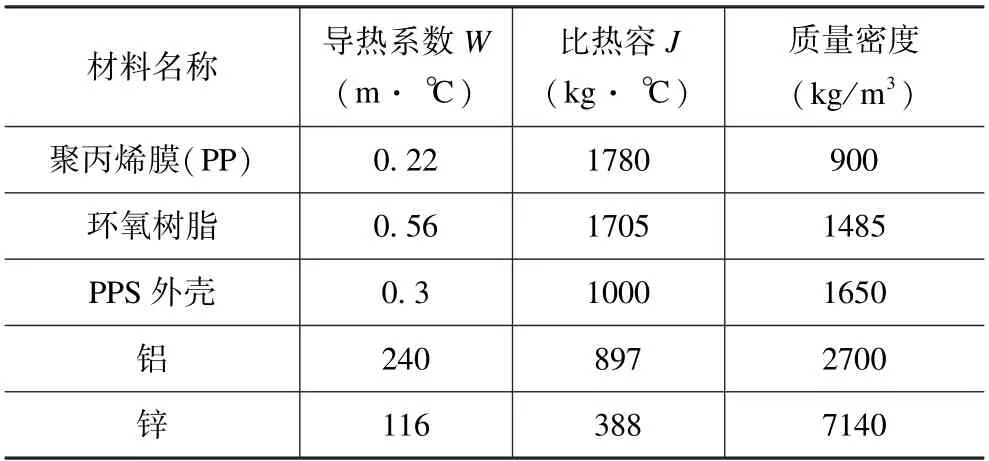
表1 电容器材料属性参数Tab.1 Material propertie sparameters of capacitor
3.4 网格划分
有限元网格划分结果直接关系仿真时间长短和计算结果准确性[15]。有限元网格划分一般分为自由网格划分、扫描网格划分、映射网格划分。自由网格划分对于单位形状没有严格限制和要求;网格划分粗细直接影响仿真时间长短和仿真计算结果,伴随着网格密度增加,计算精度随之提高,同时增加了计算时间。然而网络密度到达一定程度后,计算精度增加较少,计算时间却增加较多。由于文中研究的电容器体积小,内部填充聚氨酯形状不规则,所以综合考虑采用自由网格划分,标准网格大小为(2.8±0.14) mm,网格品质高,雅克比点: 16,计算时间: 5 s。电容器有限元自由网格划分模型见图8。

图8 电容器仿真模型网格划分Fig.8 The meshing of simulation model capacitor
3.5 仿真参数
电容器连续运行中,保压阶段是电容器不断自愈的过程,内部局部自愈产生的热量会带来温升[17]。因此为了研究电容器长期运行内部稳态温度,忽略保压阶段内部局部自愈温升的影响,电容器工作周期见图2 所示。
仿真模型边界条件和热载荷参数:T0是环境温度:17 ℃,h是综合散热系数: 6.8 W/(m· ℃),U是工作电压: 4 kV,C是电容容量: 28 μF,Ts是工作周期: 8.006 s,P0是施加的热载荷: 1.75 W。电容器内部设置温度传感器位置见图9。
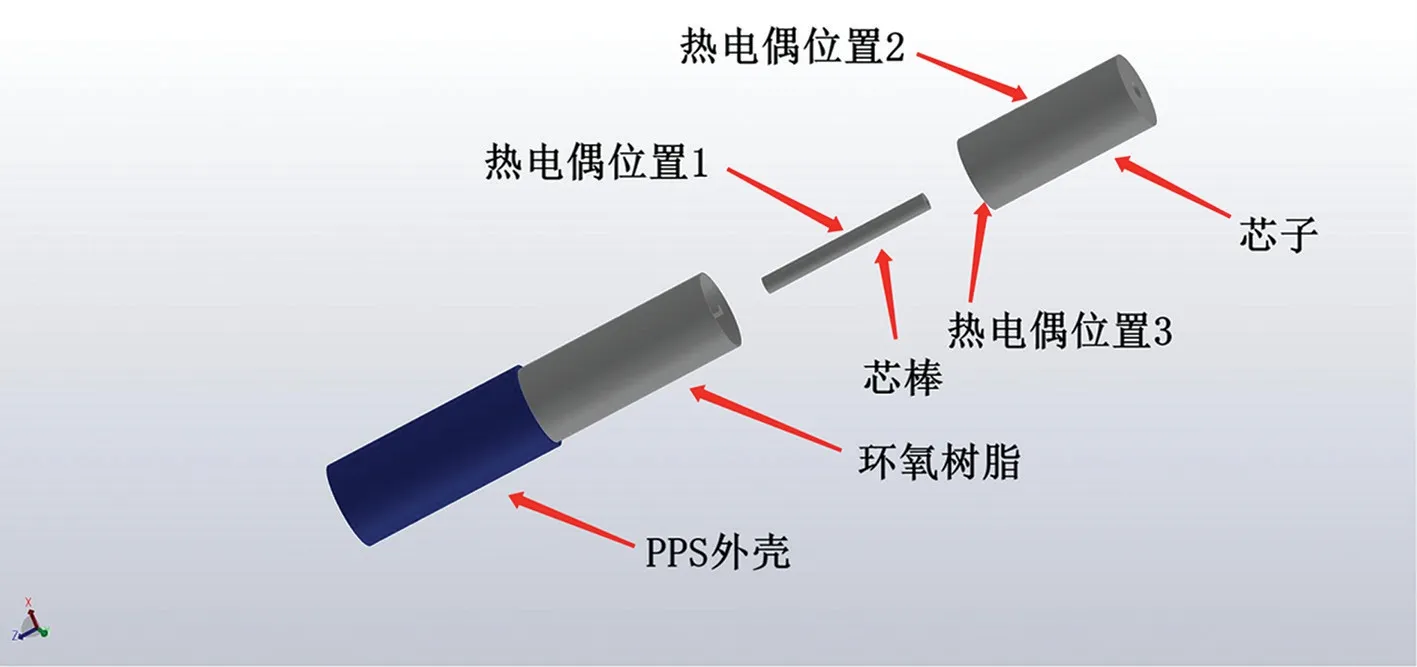
图9 电容器温度传感器分布图Fig.9 Temperaturesensor distribution diagram of capacitor
4 仿真和试验结果与讨论
为了验证仿真模型准确性,试制2 台电容器,对金属化膜电容器进行充放电试验,测量其内部不同位置温度,通过对比试验和仿真结果,验证仿真模型准确性。为了节约时间成本,假定温度增长不高于0.5℃/100 次时,电容器内部达到稳定状态。电容器实物图见图10。

图10 电容器试验实物图Fig.10 Physical diagram of capacitor
电容器试验参数:T1为环境温度: 16.9 ℃,h为综合散热系数: 6.8 W/(m· ℃),C为电容器容量: 28 μF,U1为额定电压: 4 kV,Tr1为单次充放电时间: 8 s。
4.1 仿真结果及分析
保持环境温度和综合散热条件不变,对电容器施加热载荷模拟其放电产生热量,电容器高重复频率工作后内部温度达到稳态,电容器工作稳态温度分布图见图11。可见,电容器芯子中心靠近芯管处温度最高,位置2 温度高于位置3 温度,位置1 温度高于位置3 温度。

图11 电容器脉冲工作温度分布图Fig.11 Distribution temperature chart of capacitor in pulse condition
4.2 试验结果及分析
为了进一步研究电容器实际运行过程中内部温度分布情况,在电容器内部预埋热电偶,位置分别在芯子中心位置、芯子喷金上端面和芯子外包膜。本文以电容器1 次充放电试验时间和间隔时间为电容器1 次脉冲工作周期。对#1、#2 电容器进行高频次脉冲工作试验,#1、#2 电容器脉冲工作后对电容器内部热电偶进行采样数据见表2、图12 和图13,试验与仿真结果对比见表3。
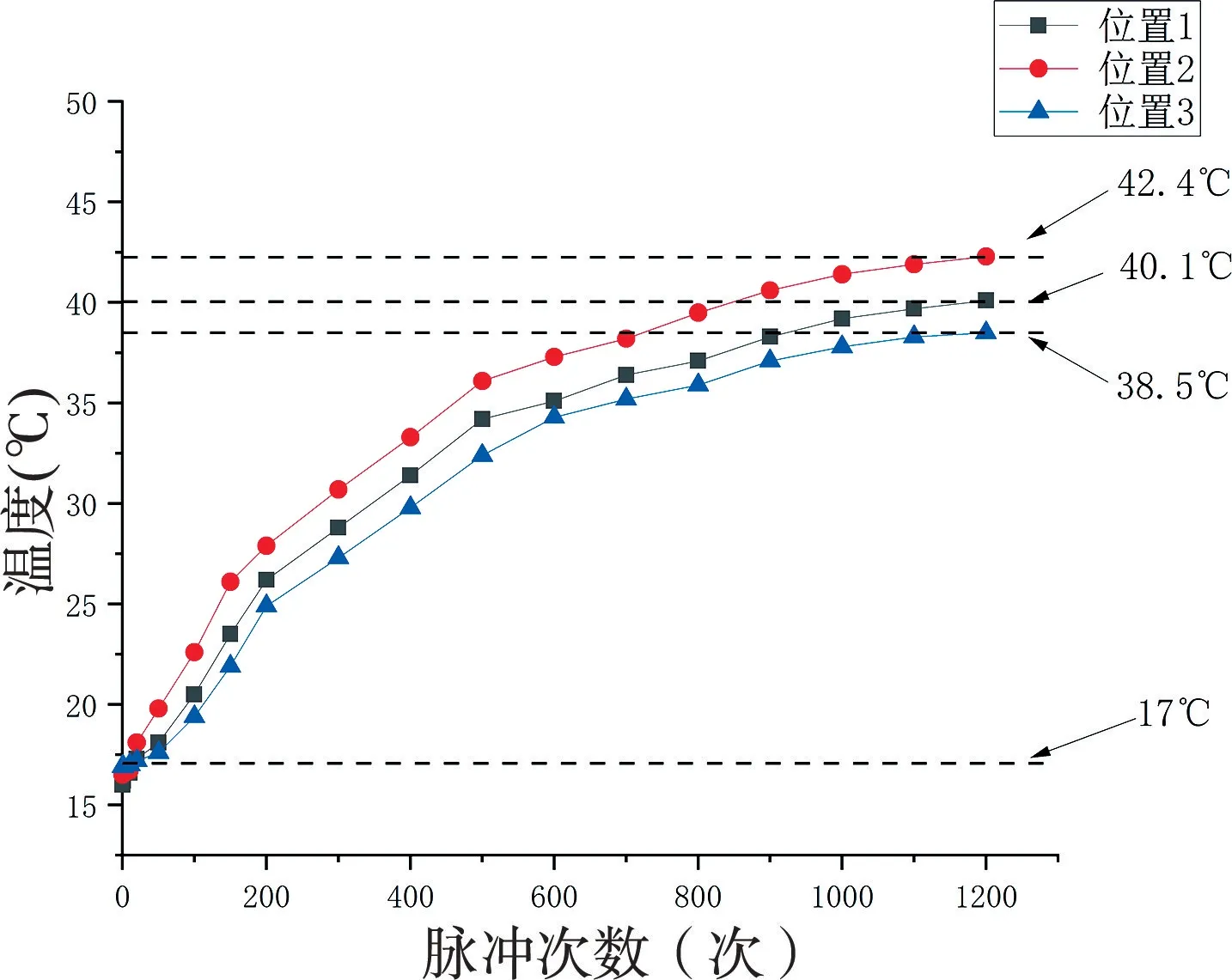
图13 #2 电容器脉冲工作温度分布趋势图Fig.13 Test temperature distribution trend of #2 capacitor in pulse condition
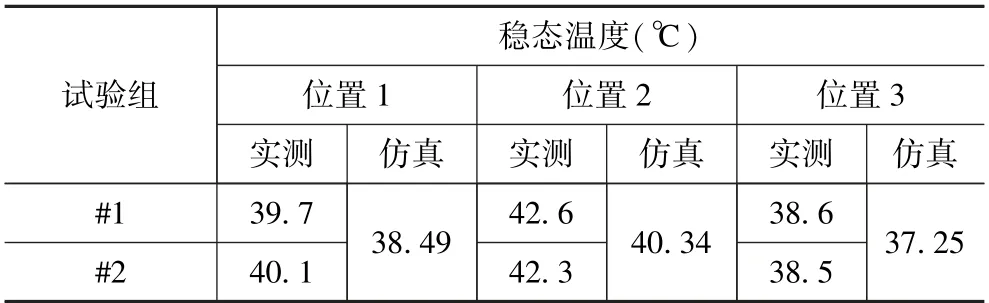
表3 试验与仿真稳态温度对比Tab.3 Comparison of test and simulation steady-state temperature
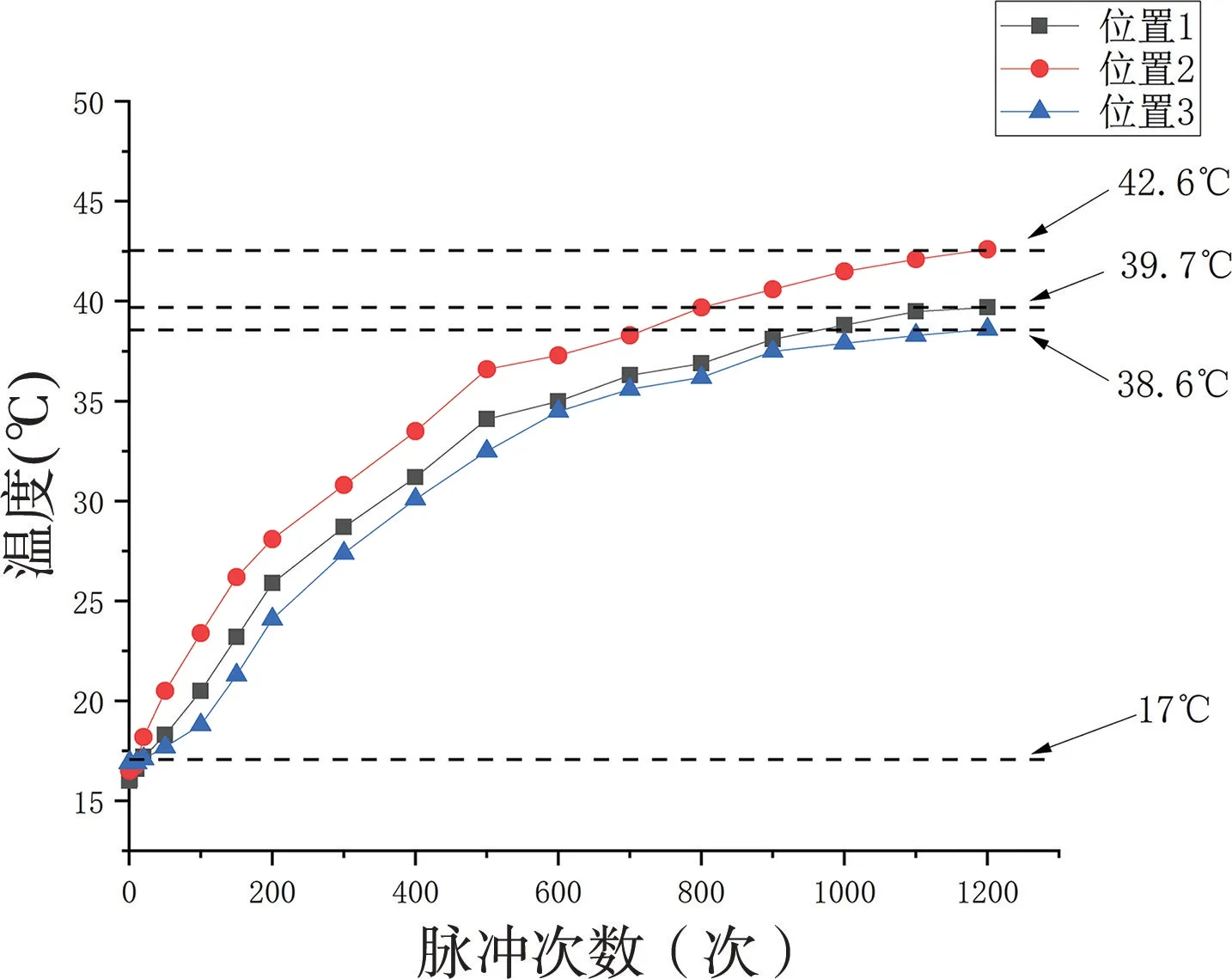
图12 #1 电容器脉冲工作温度分布趋势图Fig.12 Test temperature distribution trend of #1 capacitor in pulse condition

表2 电容器脉冲工作试验数据Tab.2 Test data of capacitor in pulse condition
由表3 可知,仿真与试验结果吻合度高,仿真模型可以较好地反映电容器内部稳态温度。
5 电容器优化设计
电容器实际工作过程中,考虑到恶劣环境因素、系统超负荷运转的影响,有必要对电容进行优化设计,降低电容器运行的稳态温度[18]。假设电容器容量、额定电压和介质耐压强度一致,环境温度: 17℃,综合散热系数: 6.8 W/(m· ℃),施加热载荷: 1.75 W。
5.1 金属化膜厚和膜宽的选择
电容器的容量相同、工作电压相同和介质耐压强度相同是选择金属化膜厚和膜宽的前提条件。
单个电容器芯子金属电极发热功率P发热为:
式中:ρ为金属化膜电阻率;d为金属化膜厚度。
n个电容芯子金属电极Pn发热发热功率为:
由式(13)可知,电容器电极发热与膜厚成反比,较大膜厚电容器的发热功率较小,电容器整体内部温升更小。
保持金属化膜膜宽一致,改变膜厚建立芯子模型导入电容器模型;保持膜厚一致,改变膜宽建立芯子模型导入电容器模型。其热分析结果见表4 和表5。
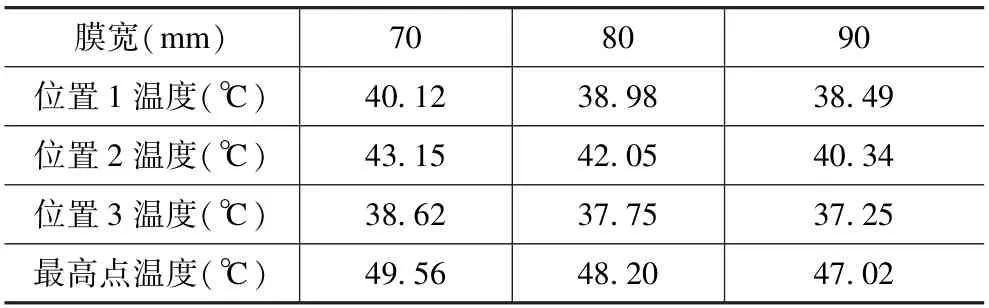
表5 不同膜宽电容器仿真稳态温度Tab.5 Comparison of steady-state temperature simulation of capacitors with different film widths
由表4 可知,膜宽一致时,增加膜厚会降低电容器内部温度。

表4 不同膜厚电容器仿真稳态温度Tab.4 Comparison of steady-state temperature simulation of capacitors with different film thicknesses
由表5 可知,膜厚一致时,增加膜宽会降低电容器内部温度。为了降低电容器运行时温度,本文样品最优设计方案为: 膜厚为8 μm 和膜宽90 mm 的卷绕参数设计方案。
5.2 电容器工作周期的选择
一般脉冲电容器工作温度为: -40~55 ℃[19],因此可通过优化工作周期使电容器处于正常工作温度范围内,对于保证电容器稳定运行尤为重要。假定单个充放电周期对电容器施加热载荷为P0,发热功率为Q;n次电容器发热功率为Qn,可以得到:
为了验证不同工作周期对电容器持续工作温升的影响,通过施加不同热载荷,可以得到不同模型稳态温度分布和最高点温度变化见表6。
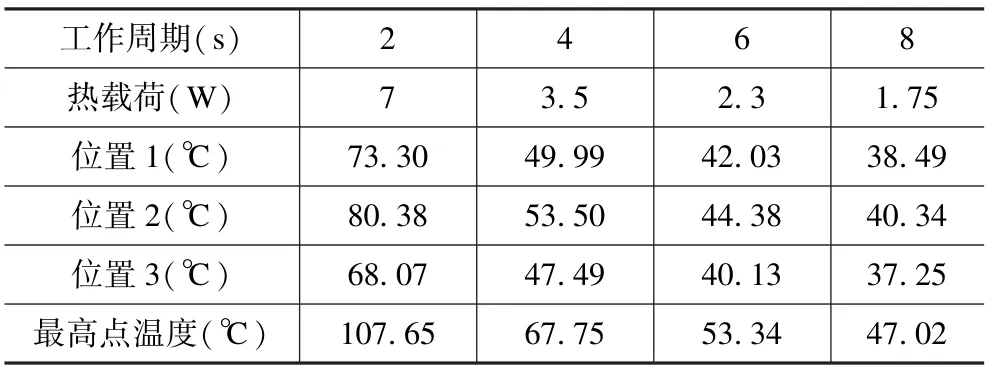
表6 不同工作周期电容器仿真稳态温度Tab.6 Comparison of steady-state temperature simulation of capacitors with different working periods
由表6 可知,电容器在工作温度范围内,适当加长工作周期能有效降低电容器工作内部温升。通过仿真计算可知,电容器运行温升最低最优方案为: 工作周期为8 s 的设计方案。
6 结论
本文分析了金属化膜电容器热传导过程和金属化膜导热各向异性。基于以上条件建立电容器仿真模型,研究了脉冲用电容器稳态温度,试验结果验证了仿真模型的准确性。在额定工况下,电容器工作过高温升会影响其工作性能,合理优化电容器金属化膜卷绕参数和工作周期参数设置对脉冲电容器设计有一定指导意义。
