高效率双频连续F 类功率放大器的设计

王帅,段亚朋,毋皓,安万通,李晓明

(河南理工大学 电气工程与自动化学院,河南 焦作 454000)

随着通信技术的快速发展和应用需求的多样化,越来越多的应用场景要求通信设备具备良好的多标准兼容性,进而要求射频发射系统在多频段工作条件下仍能保持良好的性能[1]。射频功率放大器作为射频前端关键且耗能最大的器件之一,高效率的宽带和多频段功放设计技术已成为近年来热门的研究方向。

连续F 类[2]、宽带E 类[3]和谐波调谐[4]等方法为宽带高效率功放的设计提供了参考,然而使用精确的谐波控制来提高效率的方法很难应用于宽带功放的整个频带,对于通信标准中的一些特殊频段,使用多频段的功放设计更有优势。因此,多频段功放的设计引起了人们的广泛关注。Wang 等[5]通过在匹配网络中加入并联谐振电路,分别对两个频段的最佳基波阻抗进行匹配,实现双频工作。但由于未考虑到谐波阻抗的影响,所设计的功放实际效率不高。提高双频功放效率常用开关类功放,Kalim 等[6]和Ji 等[7]分别介绍了双频E 类功放的设计方法,由于E 类功放提供了所有谐波的中间值阻抗且受限于E 类功放输出电容的影响,双频E 类对高效率的贡献并不理想。相较于开关E 类功放,谐波控制类的最大漏级效率不受输出端电容的影响,因此,在提高效率方面具有更大的潜力。Pang 等[8]和Zhang 等[9]基于高次谐波在Smith 圆图上的分布,通过优化双频谐波抑制网络,将两个频点的高次谐波控制在高效率圆交叠区域,实现了高效率性能。然而并未得出精确的双频谐波抑制网络参数,使其应用受到一定限制。

针对上述问题,本文基于连续F 类功放理论,提出了通过精确的谐波控制技术来提高双频功放效率的新方法。首先对高达三次双频谐波控制网络的参数进行了详细的理论分析,并仿真验证了新方法的可行性。然后提出了一种双频基波匹配网络设计的通用方法,并对其结构做了简化使其更易于实现。最后使用Cree公司的CGH40010F GaN HEMT 加工实现了一款高效率双频连续F 类功放,测试结果表明,在1.8 和2.6 GHz 下,可分别提供40.6 dBm 和39.5 dBm 的饱和输出功率,最大功率附加效率分别为75.4%和74%,最大漏级效率均大于75%。

1 F 类/连续F 类功放理论

谐波控制F 类功放是在过激励的B 类功放基础上发展而来的。标准的F 类功放要求偶次谐波阻抗短路,奇次谐波阻抗开路,以此在输出端产生电压方波与电流半正弦波,避免了电压电流波形交叠,理论效率达到100%,却也限制了F 类设计的阻抗空间。考虑到三次以上谐波对效率的贡献很小且控制高次谐波会进一步增加电路尺寸,因此本文只控制到三次谐波,与之对应的标准F 类功放的理论效率上限为90.7%。标准F 类漏级电压VDS和电流IDS的傅里叶展开式可表示为:

连续F 类是F 类功放的扩展[10],通过在F 类电压波形公式上添加修正因子,增加了基阻抗的解空间,同时将二次谐波阻抗从F 类的短路点改变为连续变化的纯电抗,三次谐波阻抗依然控制在开路点,扩展了F 类功放的阻抗设计空间。在连续F 类的阻抗解空间内,理论上功放能够获得与传统F 类功放相同的输出功率和漏级效率。连续F 类的漏级电压可表示为:

为了确保漏源电压始终为正值,γ在-1～1 之间取值。联立式(2)和式(3),可得基波和各次谐波阻抗值:

其中

式中:Ropt为理想B 类功放最佳基波阻抗值;Vdc和Imax分别为理想B 类功放的偏置电压和最大电流。

连续F 类在电流源平面的基波和各次谐波阻抗分布图如图1 所示。由图1 可知,当γ在[-1,1]取值时,基波阻抗由纯阻性变化为连续的复阻抗,二次谐波阻抗由短路变化为连续的纯电抗,三次谐波阻抗趋于无穷。相较于标准的F 类功放,连续F 类功放扩展了阻抗设计空间,同时兼顾了高效率的特性。

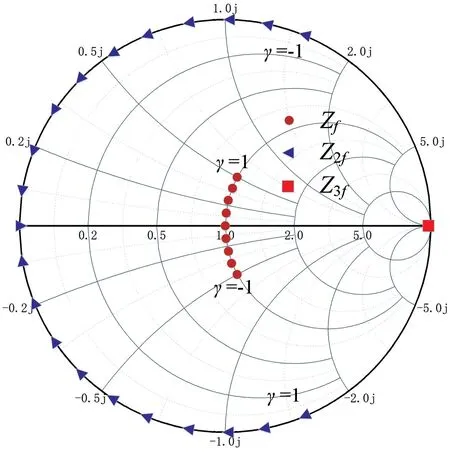
图1 γ 取[-1,1]时基波和各次谐波阻抗分布图Fig.1 γ distribution diagram of fundamental wave and harmonic impedance at [-1,1]

2 双频谐波控制网络设计

基于连续F 类的阻抗条件,需要将二次谐波阻抗控制到短路点附近,将三次谐波阻抗控制在开路点附近,以此提高功放的效率。为获得有源器件CGH40010F 的基波和各次谐波阻抗,并对其进行精确控制,本文使用ADS 软件的负载牵引模块来获得晶体管最佳基波和高次谐波阻抗进行谐波控制网络的设计。图2 给出了牵引得到的最佳基波阻抗和高次谐波阻抗在Smith 圆图上的分布结果,表1 给出了对应阻抗的具体数值。

表1 最佳基波和高次谐波参数Tab.1 Optimal fundamental and higher harmonic parameters

图2 CGH40010F 负载牵引最佳基波和高次谐波阻抗分布图Fig.2 Optimal fundamental and higher harmonic impedance distribution of CGH40010F load pull

分析基波和高次谐波负载牵引结果,使用图3 所示的双频谐波控制网络对两个频点处的二次和三次谐波分别进行短路和开路处理。推导过程如下:

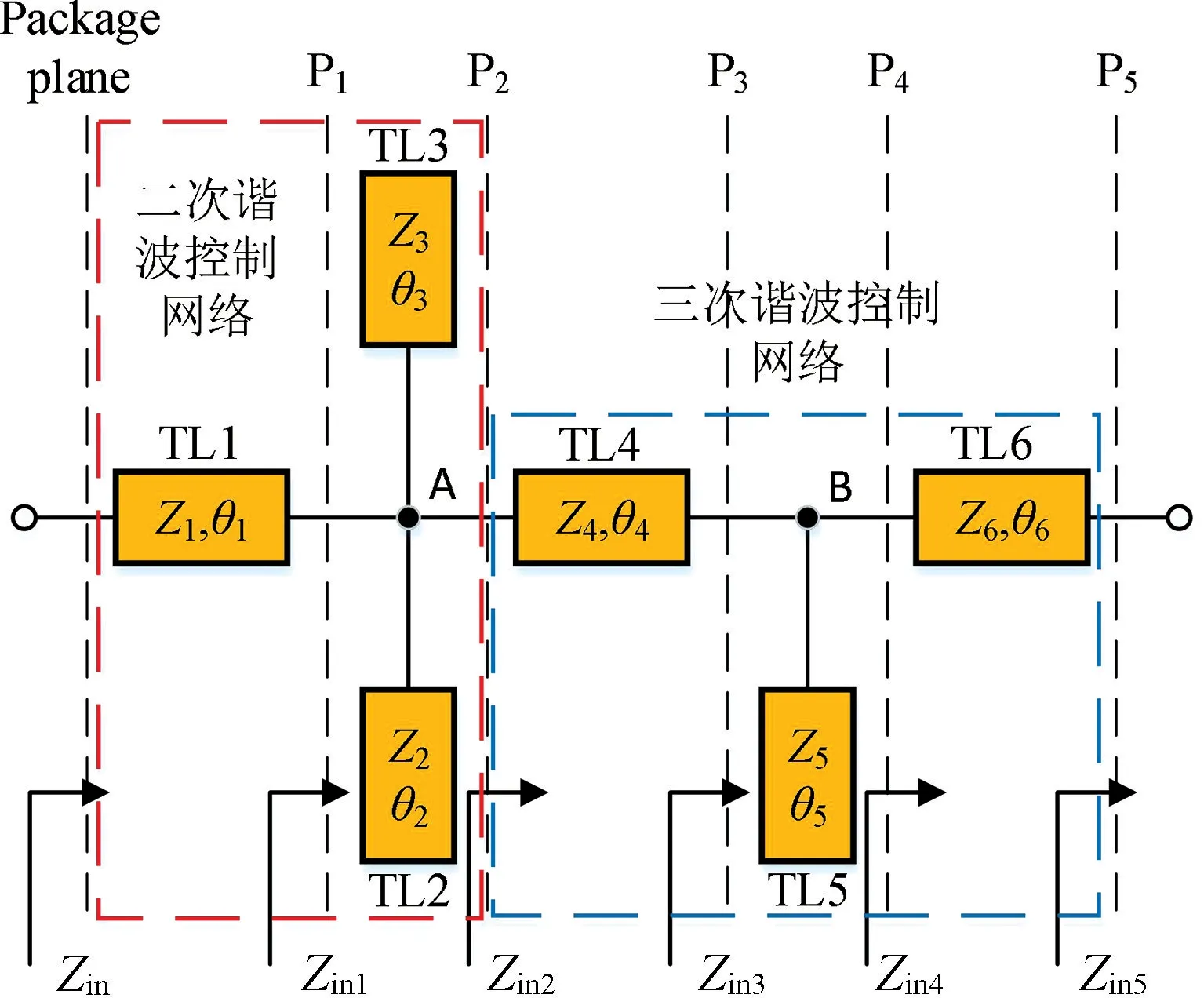
图3 双频谐波控制网络Fig.3 Dual-band harmonic control network

首先定义频率比为r,其中

式中:f1和f2分别为双频功放的中心频率。通过引入参数r,将f2处计算的参数归一化到f1处,以简化设计过程。微带TL2、TL3 用于控制两个频点的二次谐波同时在A 点处产生短路,因而将TL2 的电长度设置为频率2f1下的1/4 波长线,波长可用λ表示。换算到基频f1处,TL2 的电长度θ2为λ1/8,TL3 的电长度可用式(7)计算:

特性阻抗Z2、Z3为自由设计参数,为在基频处提供足够的阻抗,特性阻抗应尽可能的大[11]。若在A 点满足二次谐波短路条件,TL1 的参数Z1和θ1分别可由式(8)和式(9)计算得到:

在确定了Z1和θ1的参数之后,平面P1处3f1的谐波阻抗由式(10)计算得到:

同理,3f2的谐波阻抗也可由式(11)计算获得:

平面P1处的三次谐波阻抗亦可表示为平面P2处的三次谐波阻抗与微带线TL2 和TL3 的阻抗并联而来:

若B 点满足开路条件,TL4 的特性阻抗和电长度与平面P2处的三次谐波阻抗的关系可表示为:

联立式(14)和式(15),可解得Z4和θ4。TL5 和TL6 用于控制三次谐波。将TL5 的电长度θ5设置为频率3f1下的1/4 波长,换算到基频f1处即为λ1/12。TL6的电长度则由式(16)计算得到:

Z5、Z6为自由设计参数,并联枝节Z5特性阻抗需足够大,串联枝节Z6特性阻抗需相对小。这些自由参数的选择有充足的裕量,为后面的基波匹配提供了充足的设计空间。最终得到的双频谐波控制网络的参数如表2 所示,仿真结果如图4 所示。

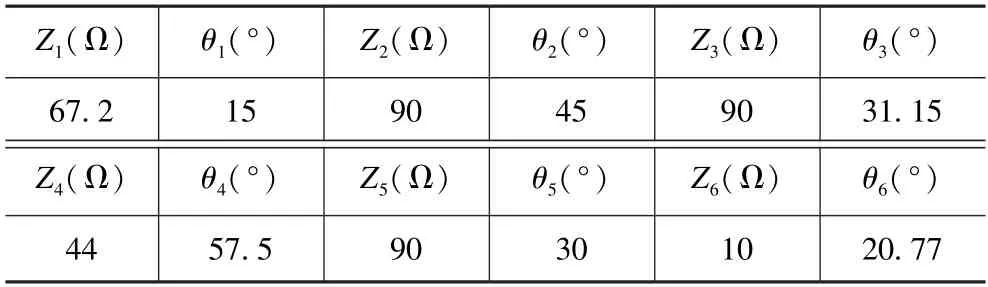
表2 谐波控制网络微带线参数表Tab.2 Parameters of microstrip line of harmonic control network

图4 双频谐波控制网络的二次、三次谐波阻抗分布图Fig.4 Second and third harmonic impedance distribution of dual-band harmonic control network

由图4 可以看出,基于上述分析设计的双频谐波控制网络各谐波阻抗参数与负载牵引的谐波阻抗结果吻合良好,说明设计的双频谐波控制网络对双频谐波起到了很好的匹配效果。至此,双频谐波控制网络的所有参数计算完毕,后续进行双频基波匹配网络的分析与设计。

3 双频基波阻抗匹配网络设计

由于设计的双频谐波控制网络在高次谐波处产生了短路点,基波匹配电路不会影响谐波控制网络。本文基于Saad 等[12]和Maktoomi 等[13]提出的双频基波匹配网络,对其结构进行了简化,提出了一种双频基波匹配网络设计的通用方法,并给出了详细的理论推导过程。图5 为设计的双频基波匹配网络结构。从图5可以看出,简化结构由三部分组成。基波阻抗ZL此时在频率f1处的阻抗为R1+jX1,同时在频率f2处的阻抗为R2+jX2,经过微带TL1 实现从平面P2看进去的双频基波阻抗为实部相同、虚部相反的共轭阻抗。

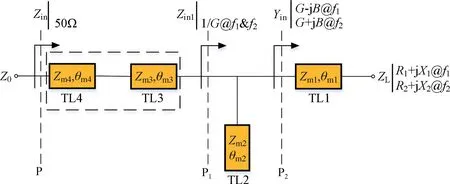
图5 双频基波匹配网络Fig.5 Dual-band fundamental matching network

微带TL1 参数推导如下:

此时,从平面P2看进去的导纳为:

并联开路微带线TL2 用于抵消共轭电抗的虚部,使得从平面P1看进去的阻抗为一实数,微带线TL2 参数推导如下:

其中,电纳B需满足

此时,从平面P1看进去的阻抗为:

最后TL3、TL4 实现Zin1处的阻抗向Zin=50 Ω 过渡。图5 虚框内的两节串联微带线结构也可以使用简单的T 形、L 形或者π 形等代替。所提出的简化基波阻抗匹配方法在实现平面P1到P 时的阻抗过渡结构可灵活选择。

4 双频功放仿真和测试

基于上述所提出的方法,本文使用ADS 仿真设计了一款工作在1.8 和2.6 GHz 的双频连续F 类功放,并对功放两个频点处的性能进行了仿真分析,验证了所提出理论的正确性。然后使用罗杰斯4350B 板材(相对介电常数为3.66,损耗角正切为0.0037),功率管采用Cree 公司的CGH40010F GaN HEMT 加工实现了一款双频连续F 类高效率功率放大器,并进行了测试验证,显示测试结果与仿真基本一致。仿真设计的双频功放整体结构如图6 所示,仿真的双频功放微带线参数已在图6 中注明,漏级电压VD和栅极电压VG分别设置为28 V 和-2.9 V。

图6 双频功放结构参数布局图Fig.6 Structure parameter layout diagrams of dual-frequency power amplifier

紧接着对双频功放的输出电压和电流波形进行了仿真分析,功放在1.8 和2.6 GHz 的电压电流波形仿真结果分别如图7(a)和(b)所示。

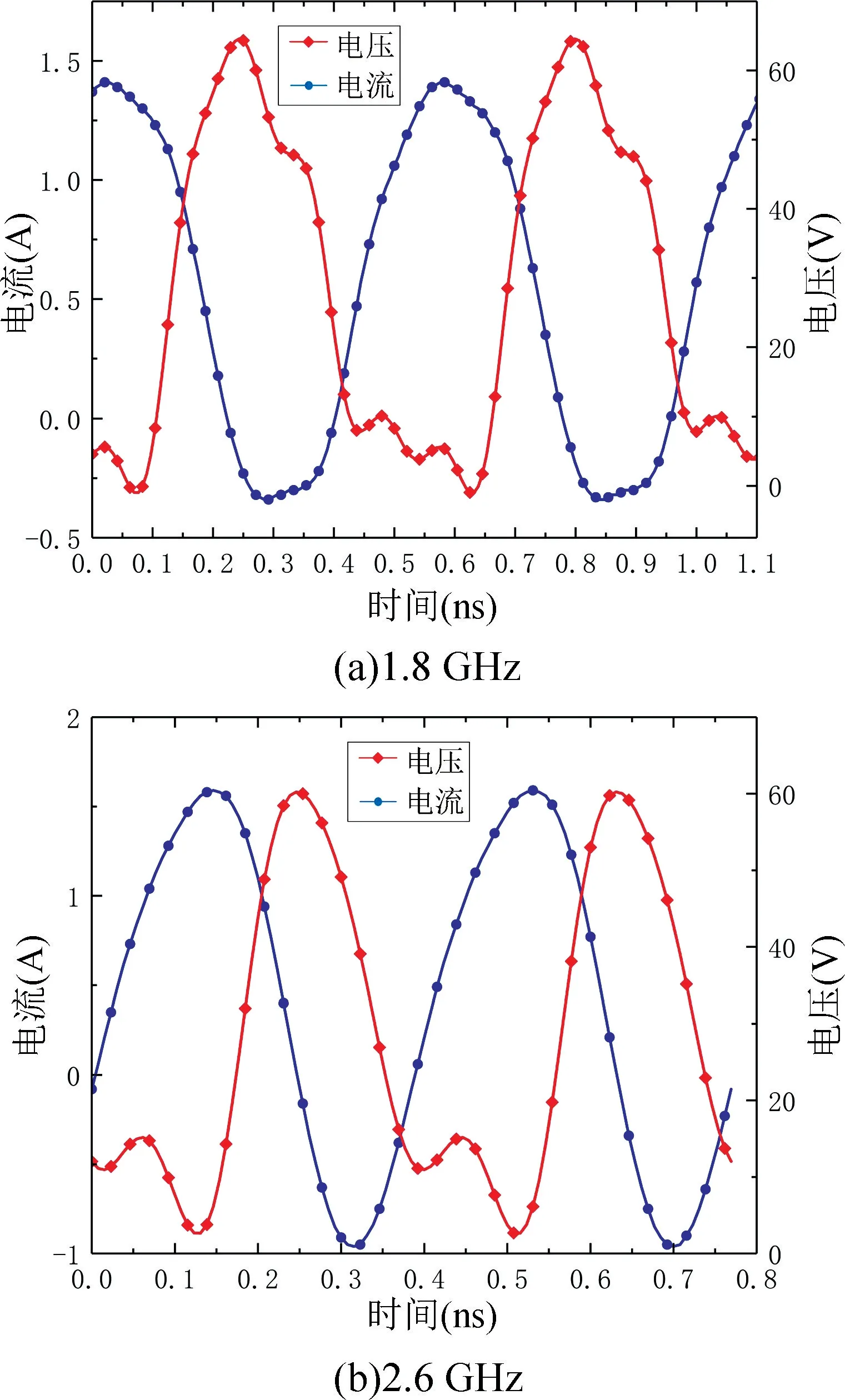
图7 1.8 和2.6 GHz 电压电流波形图Fig.7 Voltage and current waveforms at 1.8 GHz and 2.6 GHz

从图7 中可以看出,电流与标准的连续F 类电流波形接近,而电压波形由于有限的谐波控制造成与理想的连续F 类电压波形略有不同,但整体符合连续F类的工作模式。从图中可以明显看到,电压与电流波形交叠区域很小,由此减少了功率耗散,实现了双频功放的高效率。最后进行了双频功放实物的加工及测试,加工完成的实物如图8 所示,使用单音连续波信号对功放进行测试,测量功放在1.8 和2.6 GHz 下的大信号参数。

图8 双频功放加工实物图Fig.8 Photograph of the dual-band power amplifier

漏级效率(DE)和输出功率随频率的变化测量结果如图9 所示。从图9 可以看出,在1.8 GHz 处仿真的漏级效率在80%以上,输出大于40 dBm;在2.6 GHz处仿真的漏级效率也大于76%,输出在40 dBm 左右。实测功放在1.8 和2.6 GHz 处的漏级效率分别为76.6%和75.2%,饱和输出功率分别为40.6 dBm 和39.5 dBm。由于功率管封装存在不可避免的寄生参数,导致仿真与实测产生一定的误差,特别是在工作频段外,误差会更加的明显,但大体上实测与仿真结果较为符合,功放表现出明显的双频特性。

图9 1.8 和2.6 GHz DE 和输出功率与频率的关系Fig.9 DE and output power vs frequency at 1.8 GHz and 2.6 GHz

功放在1.8 和2.6 GHz 的功率附加效率(PAE)和增益与输入功率的关系分别在图10(a)和(b)中给出。从图10 中可以看出,随输入功率从10 dBm 增加至26 dBm,功放在1.8 和2.6 GHz 两个频点处的功率附加效率(PAE)的仿真与实测结果均提升至70%以上,增益在最大PAE 处均大于13 dB。实测功放在1.8 和2.6 GHz 处的功率附加效率分别为75.4%和74%,增益分别为15.5 dB 和13.6 dB。仿真与实测结果表明,本文提出的双频谐波控制网络与基波匹配网络的设计方法可以显著提升双频功放的效率。

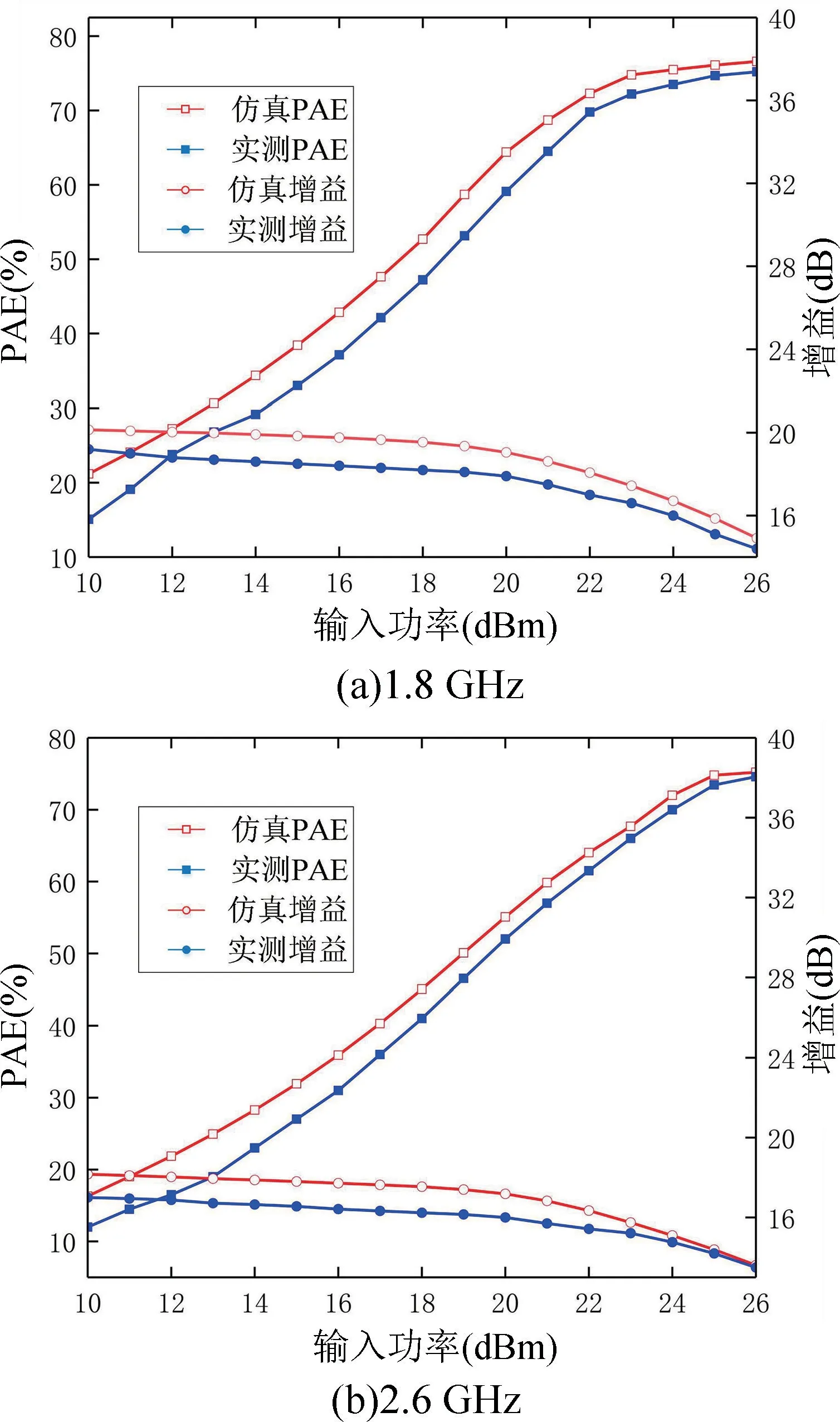
图10 1.8 和2.6 GHz PAE 和增益与输入功率的关系Fig.10 PAE and gain vs the input power at 1.8 GHz and 2.6 GHz

表3 给出了相关双频功放设计与本文设计的指标对比,结果表明,本文设计的双频功放在功率附加效率和增益等指标方面具有更好的性能。

表3 双频功放设计指标对比Tab.3 Comparison of this design and other dual-band power amplifier

5 结论

本文基于连续F 类的谐波控制理论,提出了一种高达三次谐波控制的连续F 类双频功放的设计方法,并简化了基波匹配网络,可实现任意两个频率高效率的性能,使功放实现方式更加灵活简便。基于所提出的理论,加工实现了一款工作在1.8 和2.6 GHz 的双频连续F 类功放,测试结果显示,该双频功放可分别提供40.6 dBm 和39.5 dBm 的饱和输出功率以及15.5 dB 和13.6 dB 的最大增益,功率附加效率分别可达到75.4%和74%。结果表明,本文设计的双频功放在输出功率、增益和效率等方面都表现出了优异的性能。本文设计的双频功放满足了多标准和多频段无线通信的需求,具有广阔的应用前景,为三频甚至多频高效率功放的设计提供了思路。