基于纳米孔结构的超高压石墨烯压力传感器设计

吴天金 ,孔丹,王俊强

(1.中北大学 仪器与电子学院,山西 太原 030051;2.中北大学 前沿交叉学科研究院,山西 太原 030051)

2004 年Smith 等发现由碳原子构成的蜂窝结构二维材料——石墨烯,并通过机械剥离法制作出单层石墨烯。通过对单层石墨烯的机械特性研究,Smith 等发现石墨烯的固有强度为130 GPa,杨氏模量E为1 TPa,且表面应变最高可达20%。之后Smith 等针对石墨烯优异的机械特性设计了一款悬浮式石墨烯压力传感器,主要是在压力空腔上覆盖一层石墨烯薄膜,由于空腔内部和外部之间产生压力差以致石墨烯产生应变。2013 年荷兰代尔夫特科技大学Janssen 等提出一种基于石墨烯压阻效应的压力传感器,其主要结构是厚度为100 nm,边长为280 μm×280 μm 的正方形氮化硅薄膜。Janssen 等通过有限元模拟用来分析应变分布,并将石墨烯覆盖在最大应变的区域上,通过对传感器的机电特性测量发现石墨烯的规格系数为1.6,压力传感器的动态范围为0～ 7×104Pa。2017 年Sanaeepour 等提出了纳米尺寸的石墨烯压力传感器。其主要是将石墨烯膜覆盖在以SiO2衬底的空腔上方[1-5],通过不断改变其空腔的尺寸,观察传感器的偏置电压和温度的电流-压力特性,并计算其压力传感器的灵敏度和线性误差。

以上研究表明,石墨烯薄膜的压力传感器有望应用在大量程、高精度、高灵敏度和微纳米级的测试领域。因此,需要设计一种石墨烯压力传感器的结构,以此提高石墨烯压力传感器的灵敏系数和监测范围,满足压力传感器的应用需求。石墨烯作为压力传感器的主要力敏结构,在理论和应用层面都具有重要的研究意义。目前,对石墨烯薄膜的压力敏感特性并无有效的理论模型与分析研究,本文提出了一种基于纳米孔石墨烯高压压力传感器的结构设计,通过构建氮化硼-石墨烯-氮化硼薄膜压力传感器理论模型,并结合COMSOL 仿真软件对氮化硼-石墨烯-氮化硼薄膜的压力-应变特性进行分析研究。

1 结构设计及工作原理

本文提出的一种基于纳米孔阵列式石墨烯高压压力传感器的结构,如图1 所示。主要以硅(Si)材料作为基底,开展基于纳米孔的石墨烯高压压力传感器研究。该传感器通过将石墨烯-氮化硼复合异质薄膜转移到以硅为基底的纳米通孔上,实现压力传感器力敏单元的制作。由于氮化硼具有类似于石墨的层状结构,并且其化学特性和热稳定性良好,故将氮化硼作为石墨烯的保护材料。石墨烯-氮化硼复合异质薄膜作为压力传感器的力敏单元,基于石墨烯的压阻效应能够将外界的压力信号转变为电学信号输出,从而达到对外界环境压力的检测。图2 为压力传感器的模型图,传感器的主要结构是由石墨烯-氮化硼复合异质薄膜、电极、纳米孔等组成。当传感器受到外部压力,其工作状态会发生变化,此时纳米孔上的石墨烯-氮化硼复合异质薄膜在压力作用下发生了形变,石墨烯-氮化硼复合异质薄膜形变导致中心石墨烯产生应变,应变使得石墨烯的对称六角晶格结构遭到破坏,以致石墨烯中载流子移动,石墨烯能带产生移动[6-7]。石墨烯能带的移动是石墨烯电阻变化的根本原因。由此可知,当石墨烯受到压力产生应变,则会使石墨烯的电阻发生改变。

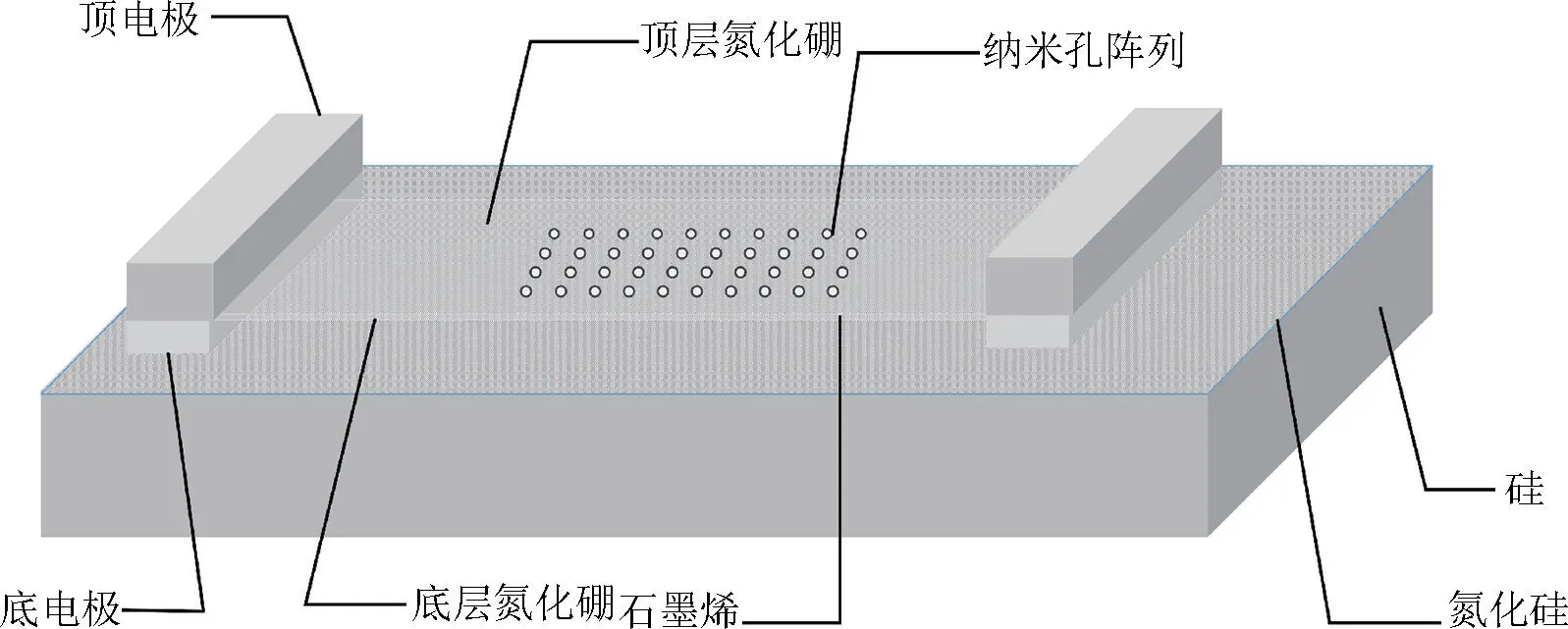
图1 传感器设计原理图Fig.1 Schematic diagram of sensor design

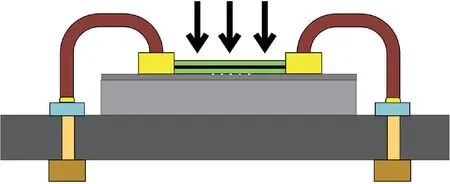
图2 传感器模型图Fig.2 Sensor model diagram

2 石墨烯压力传感器理论模型

鼓泡试验法(Bulge Test)是一种常用于分析材料力学性质的薄膜力学方法,其原理是将因受力发生形变的薄膜材料看作薄壁球壳或平板进行应力分析,通常根据材料的受力情况和实验测得材料形变量,求解材料的力学参数如杨氏模量(E)和泊松比(υ)[8-10]。本文通过将已知材料的杨氏模量、泊松比以及受力代入方程中,求解材料所产生的应变。由于考虑的薄膜受力是面压力,压强在各点处相等,故在此将面压力产生的压强称作压力。

图3 所示为石墨烯-氮化硼复合异质薄膜力学分析图。其中图3(a)为悬浮石墨烯-氮化硼复合异质薄膜受力发生形变的示意图。设硅基底上纳米孔直径为a,石墨烯-氮化硼复合异质薄膜厚度为t。当石墨烯-氮化硼复合异质薄膜受到大小为ΔP的压力时,中心产生垂直方向的最大的形变位移为δ。R为石墨烯-氮化硼复合异质薄膜的曲率半径,如图3(b)所示。取一个纳米孔径上方产生形变部分的石墨烯-氮化硼复合异质圆形薄膜进行单独研究,根据鼓泡试验法,可将其补齐为薄壁球壳进行分析,如图3(c)所示。对于薄壁球壳,壳壁的轴向正应变和周向正应变相等,记为εx,εy(εx为轴向方向,εy为周向方向),如图3(d)所示。利用截面法将球壳从球心分开为两半,选其中一部分进行分析,由截面处球壳内部应力产生的拉力与压力在该截面产生的推力相平衡的条件可得:

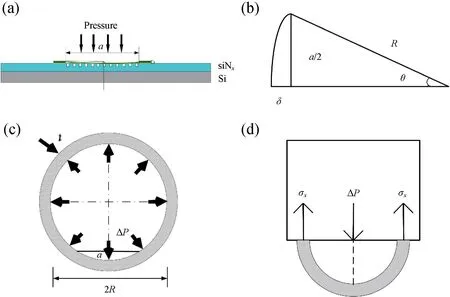
图3 (a)石墨烯薄膜受力分析;(b)形变部分薄膜的曲率半径示意图;(c)球壳模型;(d)球壳受力平衡示意图Fig.3 (a) Force analysis of graphene film;(b) Schematic diagram of the curvature radius of the deformed film;(c) Spherical shell model;(d) Schematic diagram of the force balance of spherical shell

得到球壳内部应力σ为:

根据图3(b)所示的曲率半径几何关系图(此处δ＜＜a/2),由勾股定理:

得到曲率半径R为:

忽略二阶小量,有:

将式(5)代入式(2),有:

则表面张力S为:

故石墨烯-氮化硼复合异质薄膜的应变ε:

根据图3(b)中的直角三角形可知:

所以:

由于a/2R＜1,故进行泰勒级数展开,得:

忽略高阶小量,取式(11)前两项,代入式(8),则有:

将式(5)代入式(12)得:

根据广义胡克定律,对于球壳的二向应变εx=εy=ε和二向应力σ之间存在如下关系:

故又可根据二向应变得到表面张力:

将式(13)代入式(15),得到由受到压力差而产生的表面张力SP:

则总的表面张力可表示为初始表面张力(由预应力σ0产生)S0和压力差导致的表面张力SP的和,即:

整理得圆形腔所受压力与中心形变位移的关系为:

由式(13)推导得形变与最大应变之间的关系:

将式(19)代入(18),得到压力与应变之间的关系为:

根据上述压力与应变的关系式,设定石墨烯-氮化硼复合异质薄膜的厚度h=26.35 nm,压力载荷为400 MPa,最小圆膜半径为20 nm 以及半径以4 nm 为增量,计算出了5 个不同半径对应的应变值,如图4所示。从图4 中可看出,当压力为400 MPa 时,石墨烯-氮化硼复合异质薄膜半径与应变曲线变化近似于线性关系。

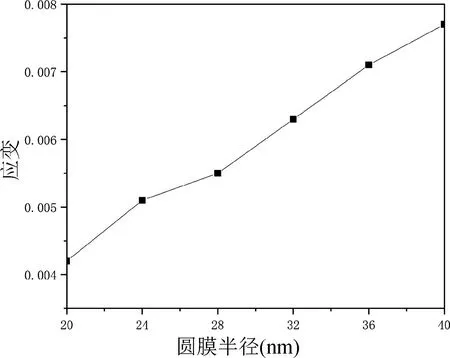
图4 理论建模计算后圆膜半径与应变的关系图Fig.4 The relationship between the radius of the circular membrane and the strain after theoretical modeling calculation

3 建模与仿真计算

基于理论建模可以对该压力传感器的石墨烯-氮化硼复合异质薄膜的压力敏感特性进行仿真分析。随着纳米孔径的增加,其纳米孔上的圆形石墨烯-氮化硼复合异质薄膜半径也增加,在石墨烯-氮化硼复合异质薄膜上方施加相同的压力时,由于石墨烯-氮化硼复合异质薄膜发生形变的程度不同,从而导致中心石墨烯产生的应变也不同,所以圆形石墨烯-氮化硼复合异质薄膜半径即纳米孔的孔径对中心石墨烯所产生应变的影响是不可忽略的。由于石墨烯的压阻效应,当石墨烯产生应变则会导致石墨烯的电阻发生改变,电阻改变就会影响传感器的输出电压。故对石墨烯-氮化硼复合异质薄膜的圆膜半径等特性进行研究,以确保在石墨烯-氮化硼复合异质薄膜上施加压力时,传感器有比较大的量程和良好的灵敏度。

为此,利用COMSOL 仿真软件进行力学仿真研究。首先需对氮化硼、石墨烯材料参数进行定义。在仿真建模之前,根据相关文献,取氮化硼、石墨烯的相关力学参数值,如表1 所示。设矩形底层氮化硼和顶层氮化硼长宽分别为: 40 μm×90 μm,40 μm×180 μm,矩形石墨烯长宽为40 μm×180 μm。

表1 各材料的力学参数Tab.1 Mechanical parameters of each material

利用COMSOL 软件分别对不同半径石墨烯-氮化硼复合异质薄膜进行仿真,主要针对其压力敏感薄膜进行仿真。本文仿真的压力模型为圆形,薄膜边缘设置为固定约束。此外,由于石墨烯-氮化硼复合异质薄膜的半径远小于其承受压力所产生的形变量,故在其仿真研究中需要考虑形变时的几何非线性,否则仿真出的结果会出现很大偏差。本次仿真采取COMSOL软件中的二维壳单元模型,其中模型含有对产生大形变物体的分析,能够给出较为精准的仿真结果。本次仿真分别设置11 组不同半径的石墨烯-氮化硼复合异质薄膜,仿真计算出400 MPa 压力下薄膜所受的最大应力、最大应变和中心位移的结果,之后将结果采用Origin 绘图软件,分别绘制出薄膜半径与最大应变、中心位移和最大应力的关系图,如图5～7 所示。由图5 可知,随着圆形石墨烯-氮化硼复合异质薄膜的半径增加,其最大应变也在增加;半径在32 nm 之后薄膜的最大应变的变化相对半径在22～32 nm 的薄膜较为平缓。图6 显示了圆形薄膜半径在20～40 nm 时中心位移的变化情况。可知,随着石墨烯-氮化硼复合异质薄膜半径逐渐增加,中心位移逐渐增大,并且当石墨烯-氮化硼复合异质薄膜半径为40 nm 时中心位移是半径为26 nm 时的2.5 倍。

图5 圆膜半径与最大应变关系图Fig.5 Relationship between the radius of the circular film and the maximum strain

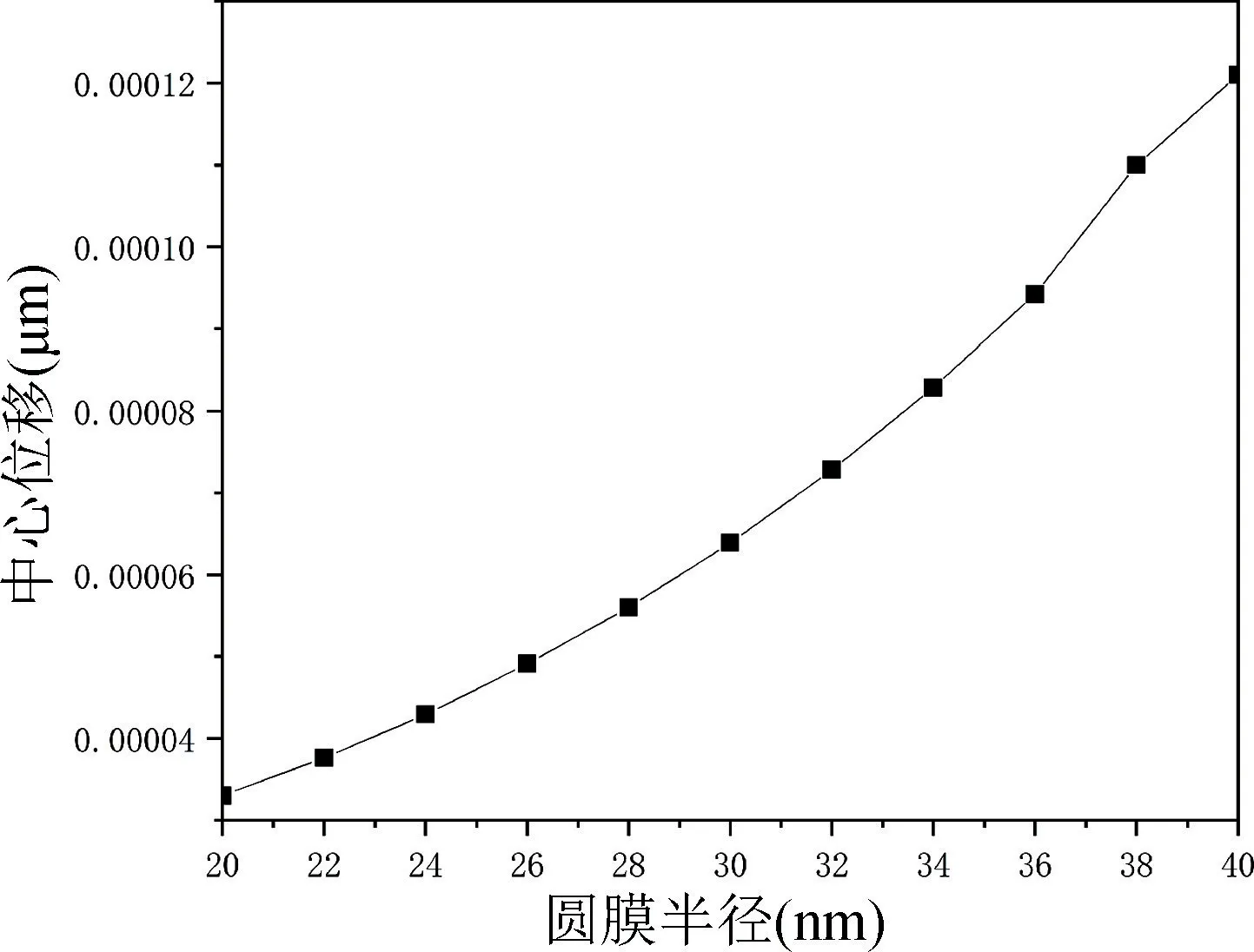
图6 圆膜半径与中心位移关系图Fig.6 Relationship between radius and center displacement of the circular film

图7 圆膜半径与最大应力关系图Fig.7 Relationship between the radius of the circular film and the maximum stress

4 仿真分析

石墨烯-氮化硼复合异质薄膜的半径大小会影响传感器整体的灵敏度和线性度,如果将石墨烯-氮化硼复合异质薄膜的半径设计过小,容易导致传感器整体的灵敏度降低;并且当复合异质薄膜半径过小即纳米孔的孔径过小,工艺难以实现[10-15]。根据表1 中氮化硼以及石墨烯材料的力学强度可知,当薄膜半径为26 nm时其最大应力在其弹性强度内且最大应变较高。因此,当石墨烯-氮化硼复合异质薄膜半径即纳米孔的孔径为26 nm时,其传感器整体的灵敏度最高。

本文设计的纳米孔结构石墨烯超高压压力传感器可应用在纳米级、高灵敏、精密测量的领域,实现石墨烯压力传感器对压力的高精度检测。通过以上分析,得出复合异质薄膜最佳半径即纳米孔孔径R为26 nm。图8～10 分别给出了最佳半径下COMSOL 仿真的应力、应变和位移云图。

图8 圆膜半径26 nm 时压力传感器应力云图Fig.8 Stress nephogram of pressure sensor with a radius of circular membrane of 26 nm

图9 圆膜半径26 nm 时压力传感器应变云图Fig.9 Strain nephogram of pressure sensor with a radius of circular membrane of 26 nm

图10 圆膜半径26 nm 时压力传感器位移云图Fig.10 Displacement nephogram of pressure sensor with a radius of circular membrane of 26 nm

5 结论

本文设计了一种基于阵列式纳米孔的石墨烯超高压压力传感器结构,利用鼓泡试验法对压力传感器结构进行理论建模,分析了在一定载荷下纳米孔半径与圆形薄膜应变之间的关系。为传感器的压力结构提供了数学模型。同时,通过COMSOL 软件进行仿真验证了上述数学模型,仿真结果与理论分析比较吻合,通过仿真分析得出了最佳的纳米孔孔径。这为纳米孔超高压石墨烯压力传感器的结构设计与压力敏感特性研究提供了一定的参考。