具有多场限环结构的SiC LDMOS 击穿特性研究

彭华溢,汪再兴,高金辉,保玉璠

(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)

随着电力电子技术的发展,越来越多的领域对于高温、高压、高功率和强辐射等极端条件下工作的功率半导体器件的需求不断增长。碳化硅(SiC)材料相较于硅(Si)材料具有更大的禁带宽度(3.2 eV)、更高的临界击穿电场(2.2 MV/cm)以及高热导率和强抗辐照能力,已经逐渐取代Si 材料成为高压功率器件的理想材料[1-2]。SiC LDMOS 因其优秀的热稳定性、高耐压能力以及更易与CMOS 工艺兼容的特性被广泛应用于高压功率集成电路,而击穿电压(VB)是LDMOS 器件结构设计的重要依据,同时也是衡量其可靠性的最重要参数。常用的提高击穿电压的方法有: 场限环、场板、槽型结构等[3-4],其中场限环制作工艺简单,成本较低,是应用最为广泛的终端结构[5-6]。为进一步提高场限环的耐压能力,国内外研究者们提出了多种优化的场限环结构[7-12]。刘岳巍等[13]提出了一种具有分组缓变间距场限环(MGM-FLR)终端结构的SiC功率MOSFET,结果表明MGM-FLR 有效调制并优化了结终端区域的表面电场强度,提高了击穿电压。Yu等[14]提出了具有步进掺杂P-top 层的Double RESURF LDMOS 结构,P-top 层在器件表面引入新的电场峰,显著提高击穿电压。Wasisto 等[15]提出了一种线性变掺杂(LVD)P-top 环LDMOS,通过优化每个环的宽度和间距使得表面电场均匀分布,进而提高击穿电压。上述研究均是基于场限环的结构、环宽、环间距对击穿电压的研究。而场限环结构的各项参数以及漂移区掺杂浓度对SiC LDMOS 击穿电压均有不同程度的影响,仍需进行全面系统的分析。

本文在传统SiC LDMOS 器件的基础上引入多场限环结构,通过器件仿真分析场限环数量、间距、掺杂浓度等参数以及漂移区掺杂浓度对击穿特性的影响。随后根据器件击穿时的表面电场分布以及电场峰值分析击穿原理,进而优化器件结构,提升击穿电压。

1 器件结构与仿真模型

图1(a)为传统SiC LDMOS 结构示意图,图1(b)为具有多场限环结构的SiC LDMOS 结构示意图。为便于表示,简称图1(a)为T-LDMOS,图1(b)为MR-LDMOS。相较于T-LDMOS 而言,MR-LDMOS 在外延层顶部加入场限环结构,从而在阻断状态下的器件表面引入新的电场峰,平衡器件表面电场分布,提高击穿电压。同时场限环辅助漂移区耗尽,可以进一步提高漂移的掺杂浓度,使得器件的特征导通电阻降低。器件结构的相关参数如表1 所示。

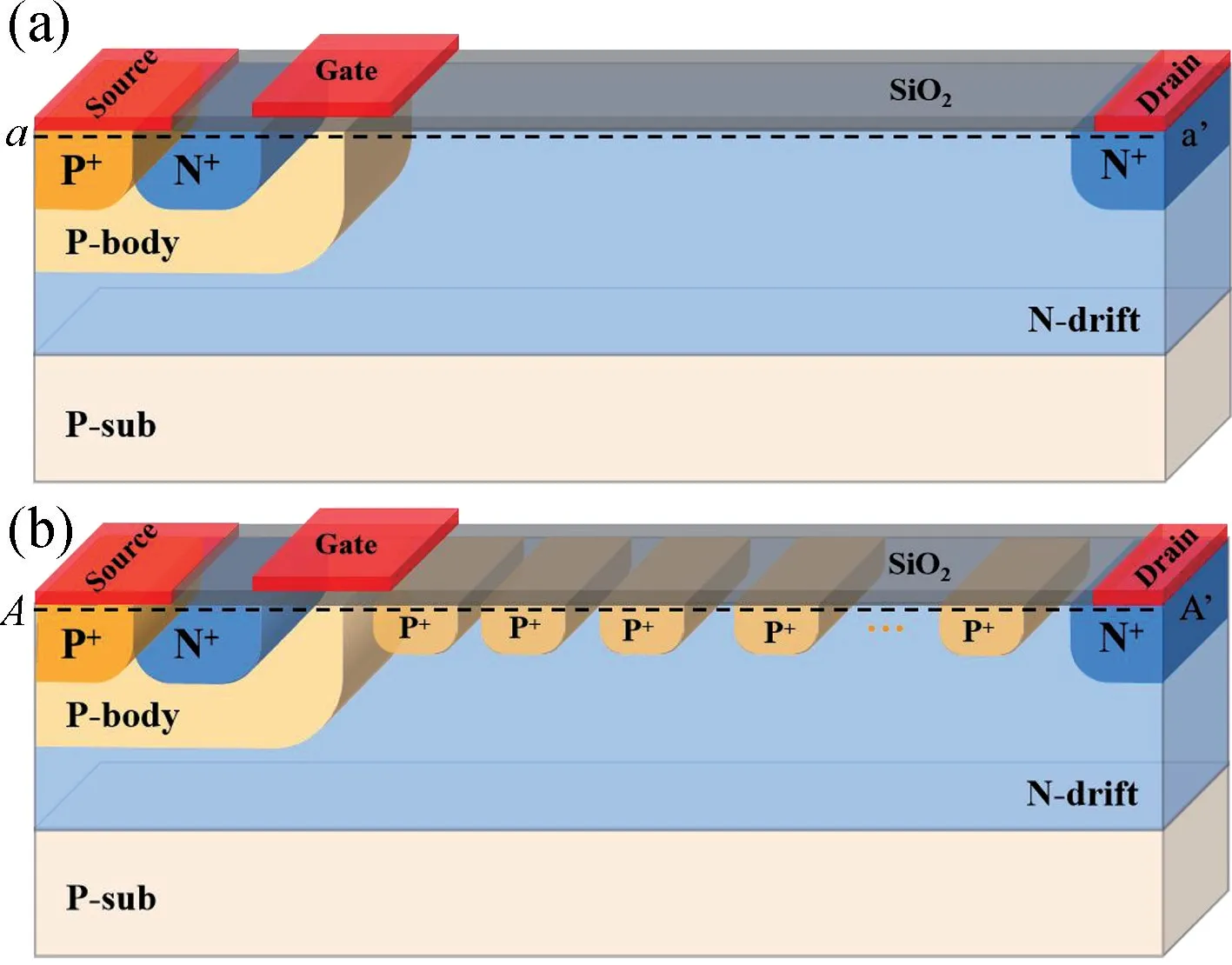
图1 (a) 传统SiC LDMOS 结构示意图;(b) 具有多场限环结构的SiC LDMOS 结构示意图Fig.1 (a) Schematic structure of T-LDMOS;(b) Schematic structure of MR-LDMOS

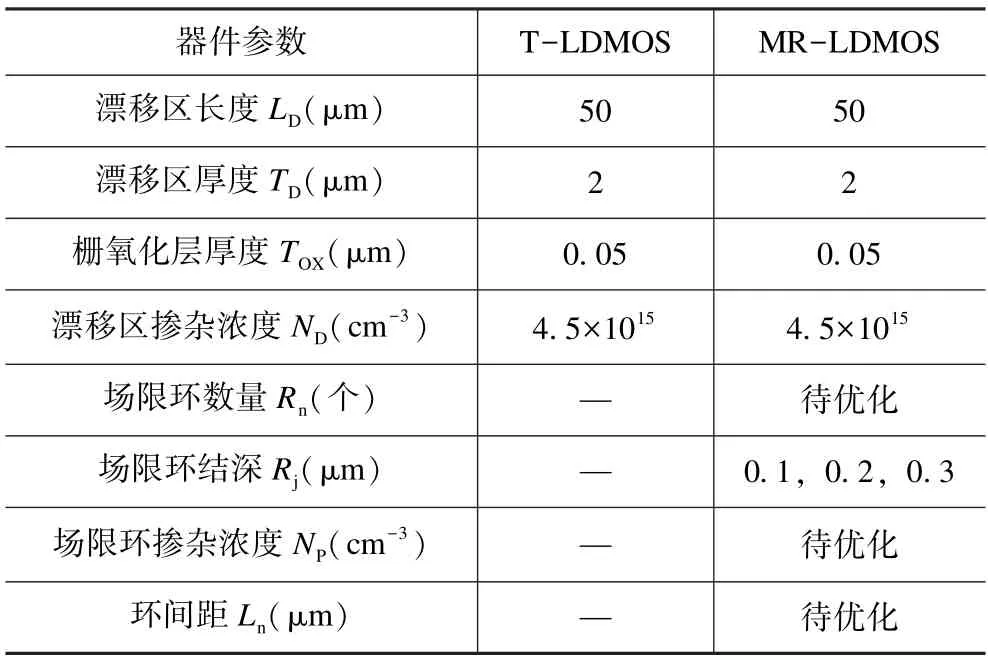
表1 器件结构相关参数Tab.1 Parameters of device structure

本文采用Slivaco TCAD 仿真软件对具有多场限环结构的SiC LDMOS 进行模拟。数值仿真时考虑到掺杂浓度、温度、横向和纵向电场的影响,迁移率模型选择CVT 模型,复合模型为Shockley-Read-Hall 和俄歇复合模型,碰撞电离模型为Selberrherr 模型,载流子统计模型为Fermi-Dirac 统计模型和能带变窄模型。

2 仿真与讨论

2.1 T-LDMOS 的击穿特性

图2 为T-LDMOS 的击穿特性曲线,阻断状态下栅极和源极接地。横轴为器件漏极电压,纵轴为漏源电流。由图可知,器件在漏极电压达到2421 V 时漏源电流快速增长,发生雪崩击穿。对于给定的漂移区掺杂浓度,T-LDMOS 的击穿表达式为:

式中:VB为击穿电压;ε0为真空介电常数;εSiC为SiC材料的相对介电常数;EC为SiC 的临界击穿电场;q为电荷量;Ndrift为漂移区掺杂浓度。根据公式(1)可计算出T-LDMOS 的理论击穿电压约为2800 V,从仿真结果可知实际击穿电压小于理论击穿电压。

图2 插图为T-LDMOS 关态击穿时的表面电场分布(沿直线aa＇,y=0.01 μm),横轴为器件横向两端的距离,纵轴为电场强度。由图可知,此时器件漂移区刚好被完全耗尽,电场在栅极边缘处聚集,形成电场峰,器件在此处发生击穿。

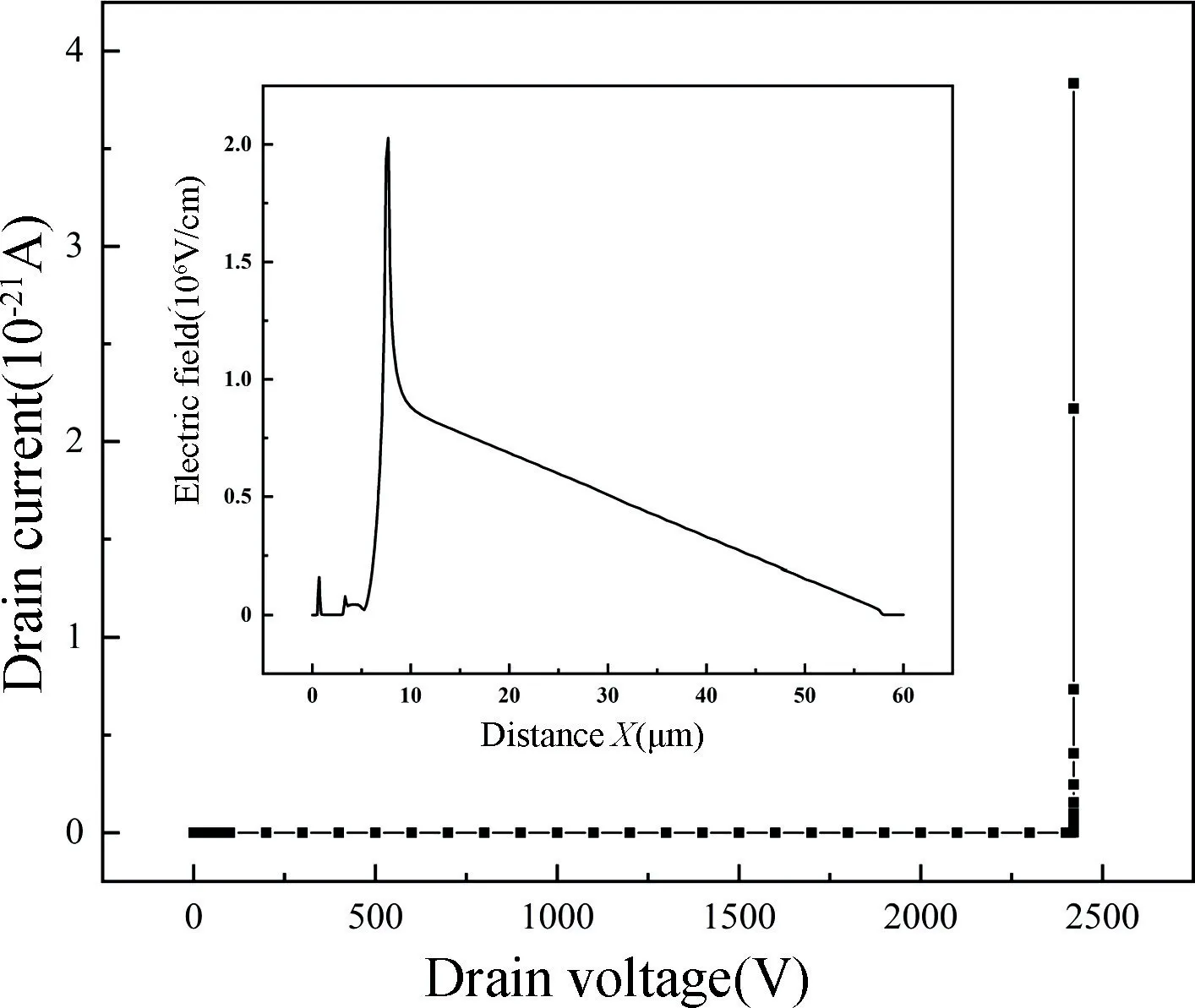
图2 T-LDMOS 的击穿特性曲线Fig.2 Breakdown characteristic curves of T-LDMOS

2.2 场限环数量对击穿特性的影响

讨论场限环数量对器件击穿特性的影响时,场限环初始位置设定在靠近栅极边缘一侧,并逐渐向漏端增加场限环数量。同时本文采用线性环间距设计,理论公式为[16]:

式中:Ln为第n级环间距;L1为第一级环间距;δ为各级环间距的增量。根据公式(2),使得L1=1μm,δ=0.1μm。ND为4.5×1015cm-3、环宽为2μm、Rj为0.2 μm,且其他参数保持不变。仅改变场限环数量Rn时,其对应的击穿特性曲线如图3 所示。随着Rn的增加,MR-LDMOS 的VB逐渐增加,最高达到5137 V,相较于T-LDMOS 的2421 V 提高了112.2%。

提取图3 数据,绘制Rn与VB的关系曲线,结果如图4 所示。器件的VB随Rn的增加呈现出先增大后减小的趋势。当Rn增加至13 时,VB达到最大值。

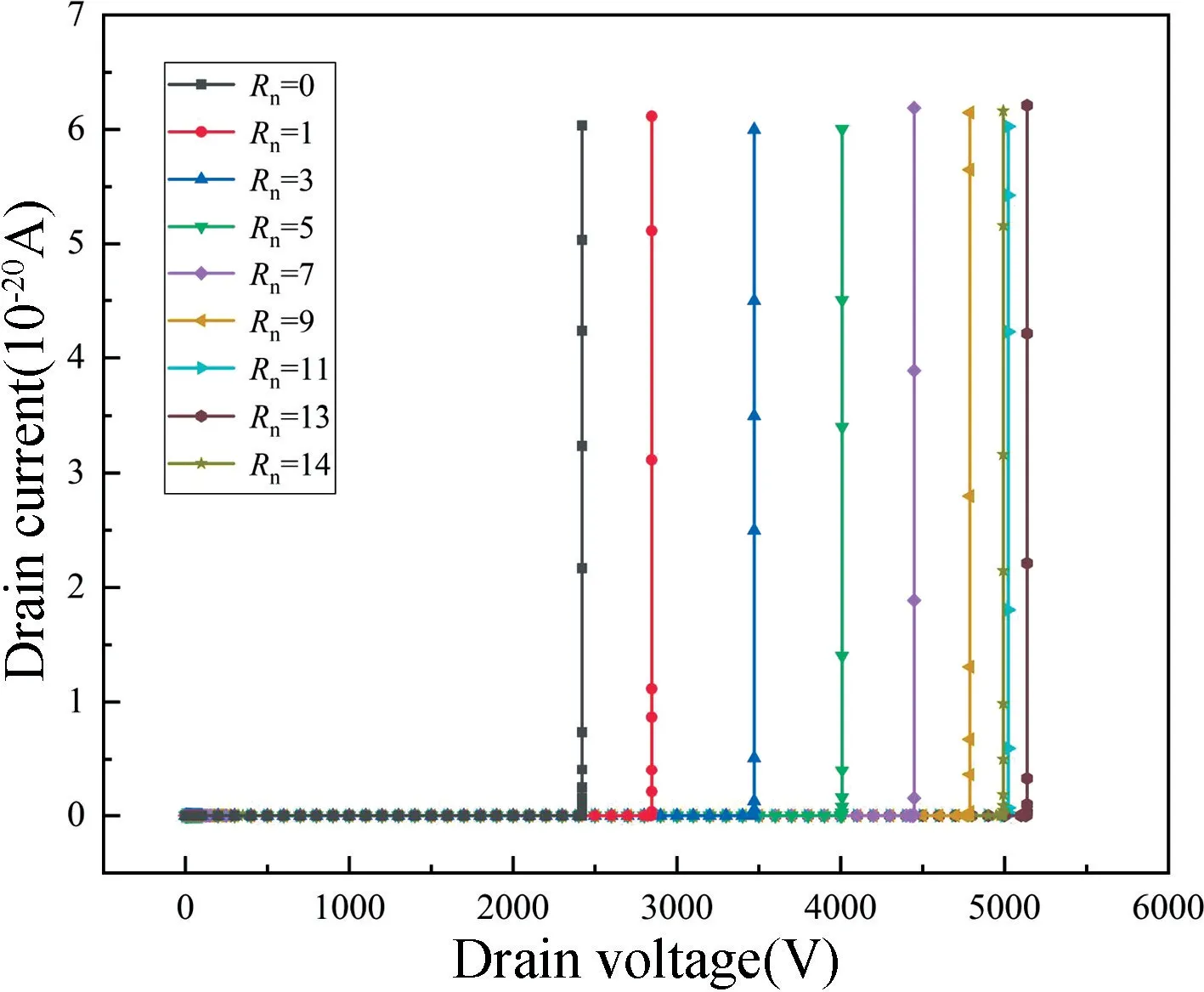
图3 不同Rn对应的击穿特性曲线Fig.3 Breakdown characteristic curves corresponding to different Rn

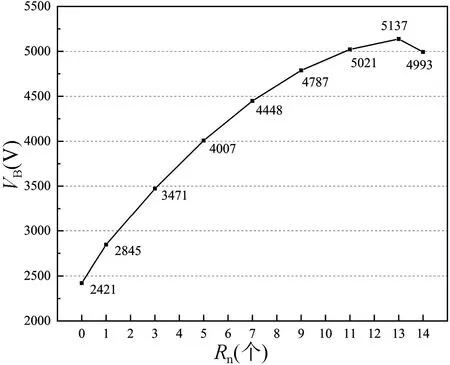
图4 Rn与VB的关系Fig.4 Relationship between Rn and VB

为进一步分析Rn影响击穿电压的机理,须分析Rn与表面电场分布之间的关系。MR-LDMOS 关态击穿时不同Rn对应的表面电场分布(沿直线AA＇,y=0.01 μm)如图5 所示。随着Rn的增大,器件表面引入更多的电场峰,进一步平衡表面电场分布,漂移区承担电场能力增强,击穿电压升高。当Rn增至13 后,继续增加Rn会使场限环距离漏极端过近,新的电场峰与漏极电场叠加,最终导致器件漏极端电场过高而提前击穿,耐压能力下降。所以在漂移区长度一定的情况下,选择Rn=13 的MR-LDMOS 作为讨论对象,进一步分析各项器件参数对击穿特性的影响。

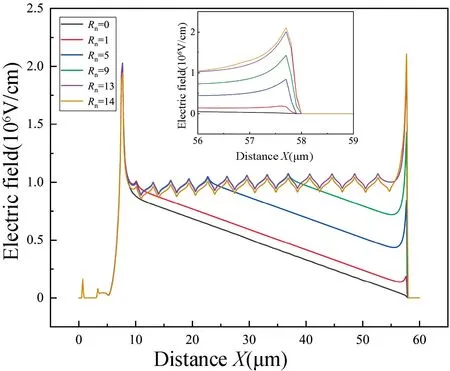
图5 不同Rn对应的关断状态表面电场分布Fig.5 Off-state surface electric field distributions corresponding to different Rn

2.3 场限环间距对击穿特性的影响

对Rn=13 的MR-LDMOS 采用两种环间距设计,分别为线性间距设计和等间距设计。

根据公式(2),对于线性间距设计器件使得L1=1 μm,δ=0.1 μm,等间距设计器件的环间距L=1.5 μm,在保证二者占用漂移区长度几乎相同的情况下进行仿真分析。

MR-LDMOS 关态击穿时不同环间距结构对应的表面电场分布(沿直线AA＇)如图6 所示,横轴为第一级到最后一级场限环的距离,纵轴为电场强度。由图可知,随着电场峰向漏极端靠近,两种环间距结构器件的表面电场呈现出不同的分布趋势。等环间距器件的电场峰值呈现出单调递增趋势,线性环间距器件的电场峰值先缓增,并在第8 个电场峰后保持不变。二者在第12 个电场峰处的峰值相同,之后等环间距器件的电场峰值高于线性环间距器件的电场峰值。

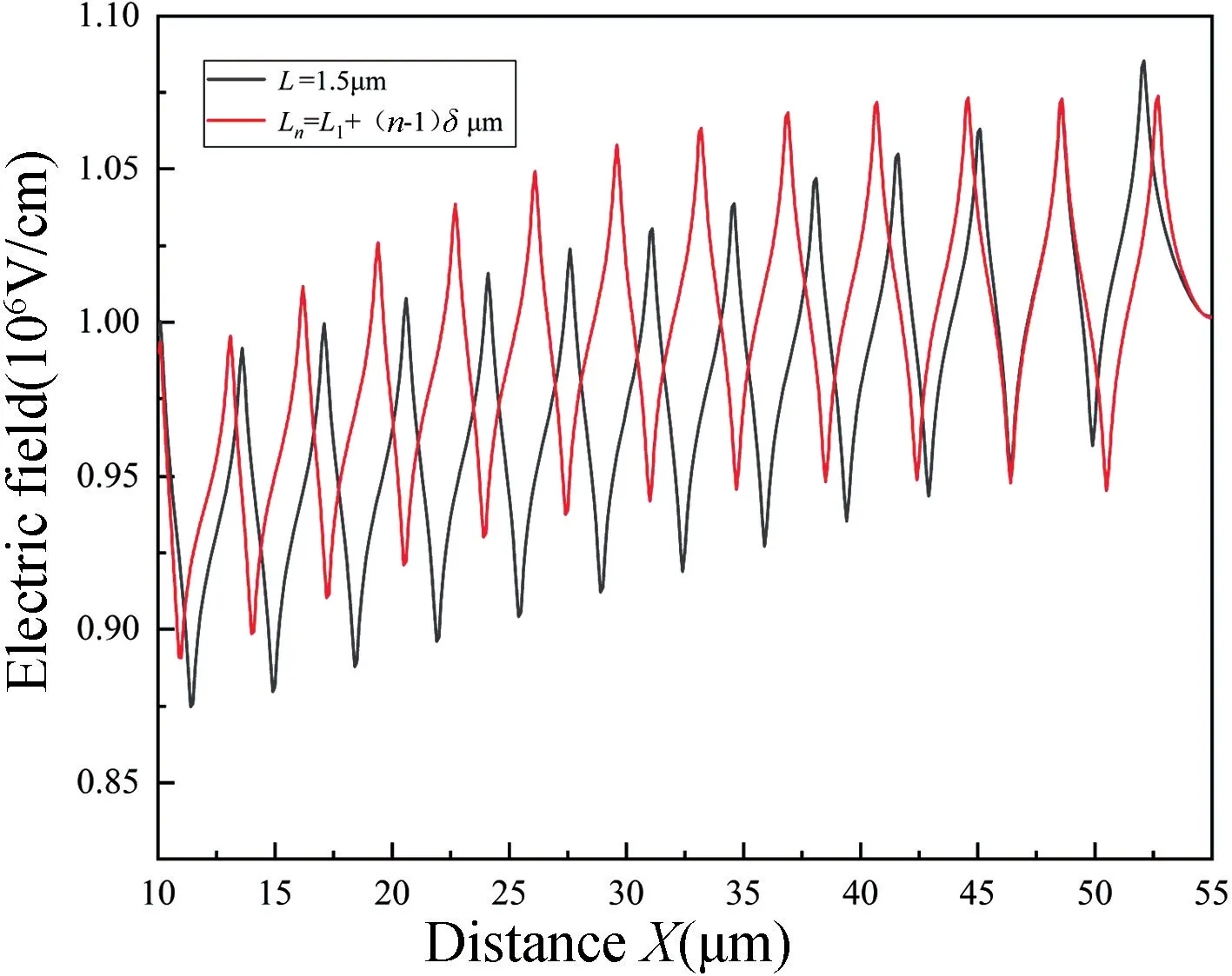
图6 不同环间距结构对应的关断状态表面电场分布Fig.6 Off-state surface electric field distribution corresponding to different ring spacing structures

经对比,线性环间距MR-LDMOS 的平均电场强度高于等环间距MR-LDMOS,击穿电压更高,并且随着环数量的增多,后者靠近漏极端的电场峰值过高,更易导致漏极提前击穿,器件可靠性下降。综合考虑,线性环间距设计的MR-LDMOS 耐压能力更好,性能更为优秀。

2.4 场限环掺杂浓度对击穿特性的影响

不同NP对MR-LDMOS 击穿特性的影响如图7 所示。数值模拟过程中,ND=4.5×1015cm-3,Rj=0.2 μm,其他参数保持不变,仅改变NP。由图可知,当NP=3.5×1016cm-3时,VB达到最大值。

根据图7 数据,绘制NP与击穿电压VB的关系曲线,如图8 所示。当NP分别为1.5×1016,3.5×1016和5.5×1016cm-3时,VB分别为3995,5137 和4861 V。随着NP的增大,VB先增大后减小。

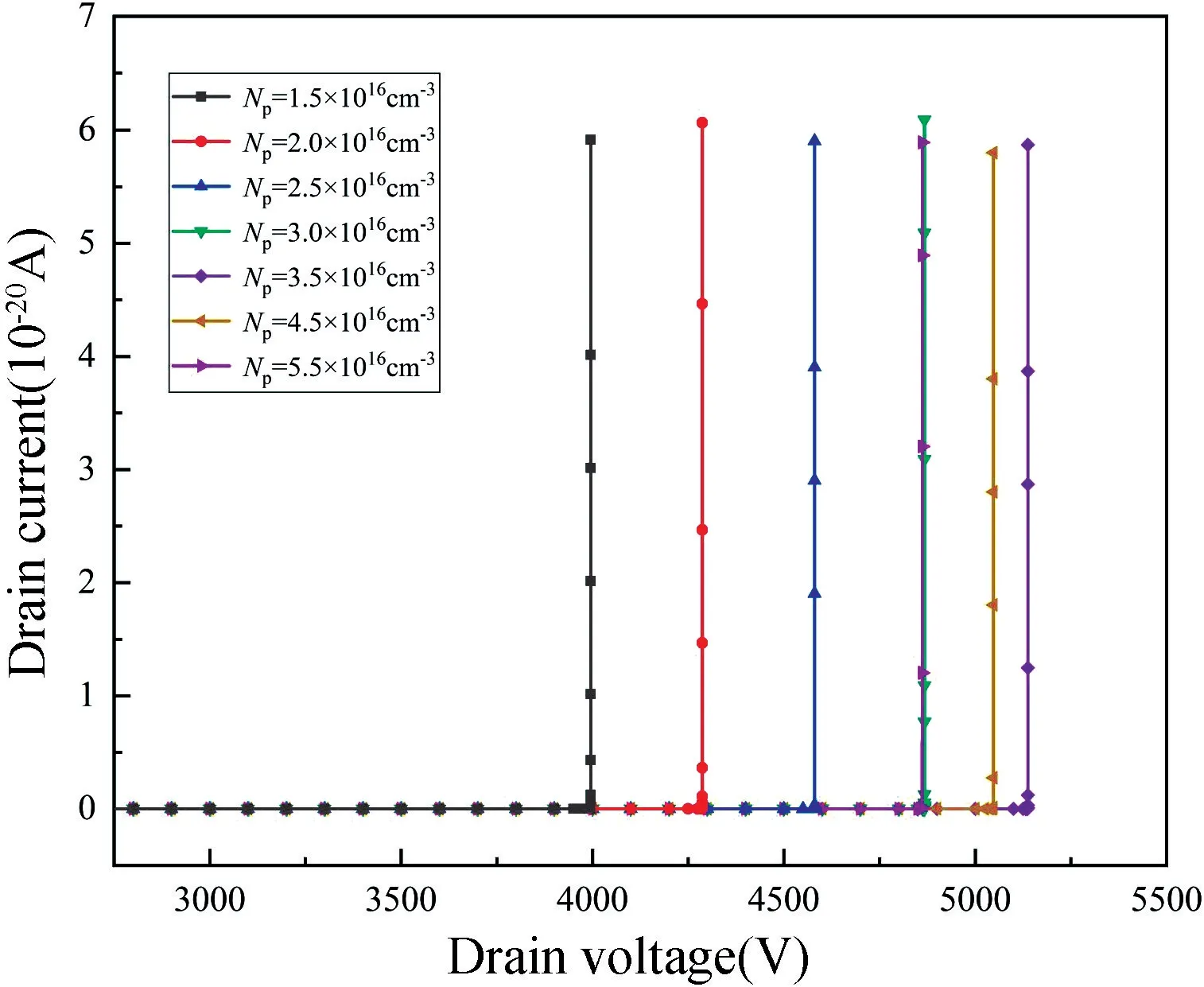
图7 不同NP对应的击穿特性曲线Fig.7 Breakdown characteristic curves corresponding to different NP

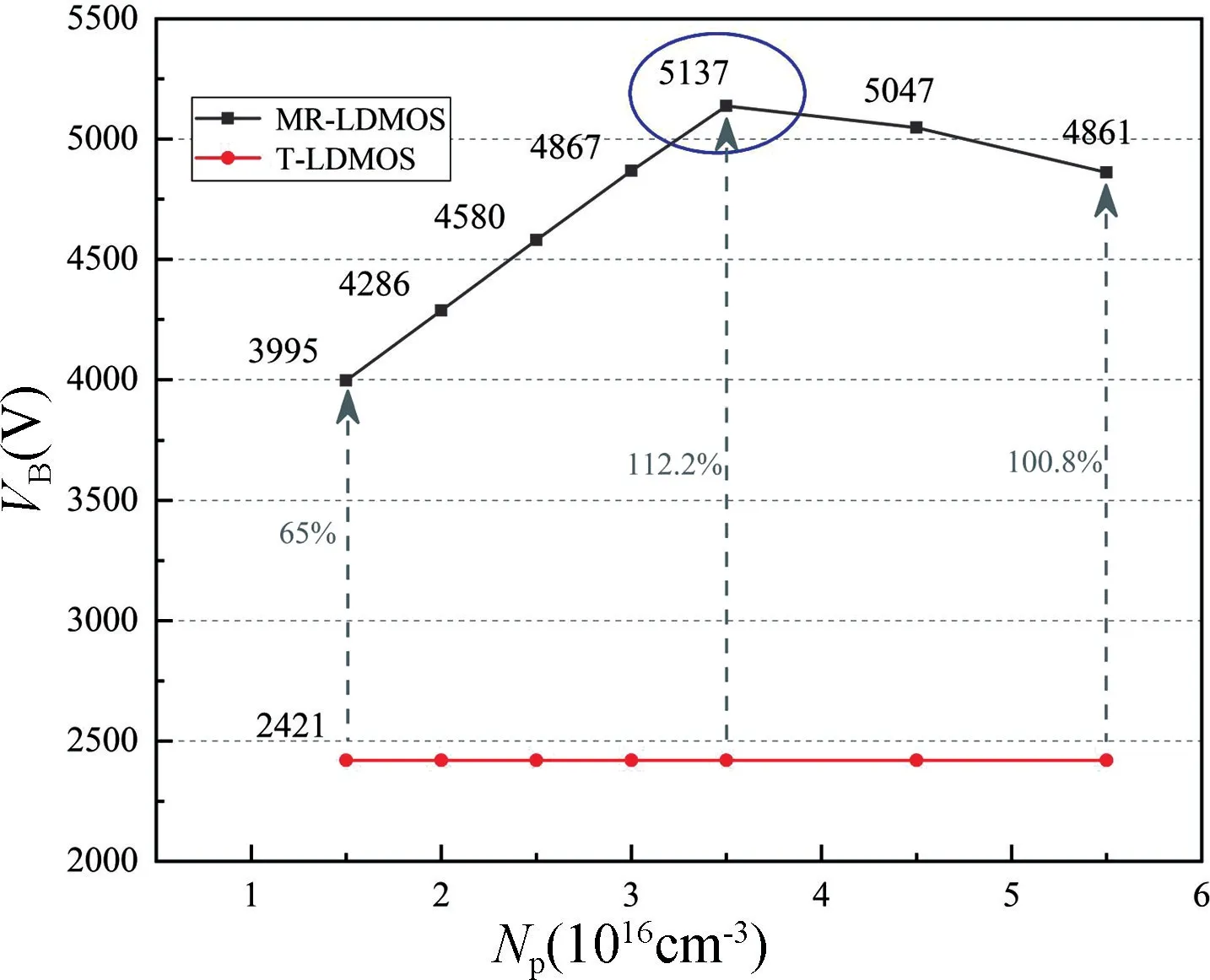
图8 NP与VB的关系Fig.8 Relationship between NP and VB

为了进一步分析NP影响击穿电压的机理,须分析NP与表面电场分布之间的关系。MR-LDMOS 发生关态击穿时不同NP对应的表面电场分布(沿直线AA＇)如图9 所示。由图可知,场限环结构在器件漂移区表面引入多个电场峰,对比T-LDMOS,MR-LDMOS 的漂移区表面电场强度更高且电场分布更为均匀,更为充分利用漂移区来承担电场,击穿电压得到提升。同时,随着NP的增大,电场峰更为尖锐,峰值更高。这是由于随着NP的增大,场限环辅助耗尽漂移区的能力增强,加速漂移区的耗尽,从而在器件表面引入更高的电场峰。

相较总体而言,并非单个电场峰值越高的器件击穿电压越高。由图9 插图可知,随着NP的增大,器件漏极端的电场强度不断升高。当NP分别为1.5×1016,3.5×1016和4.5×1016cm-3时,漏极端电场强度分别为1.2×106,2.0×106和2.2×106V/cm。当NP继续增大,漏极端电场强度保持不变,此时漏极端的电场强度达到了SiC 材料的临界击穿电场,器件击穿点从栅极边缘下方转移到漏极端,导致提前击穿,击穿电压下降。图10 给出了器件关态击穿时漂移区内电场分布。由图可知,NP=3.5×1016cm-3时,漂移区内部平均电场强度保持在1×106V/cm 左右,电场分布近似为矩形分布。由此可得出,当器件栅极边缘处的电场强度与漏极端电场强度相等时,漂移区表面电场和内部电场分布最为均匀,器件的击穿电压达到最大值。

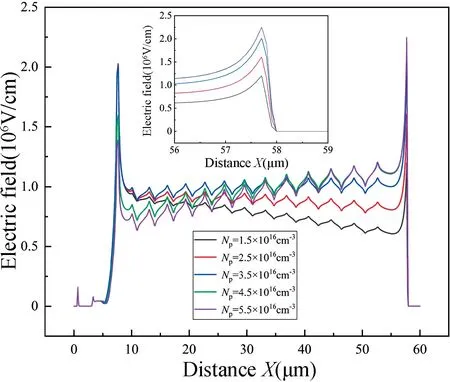
图9 不同NP对应的关断状态表面电场分布Fig.9 Off-state surface electric field distributions corresponding to different NP

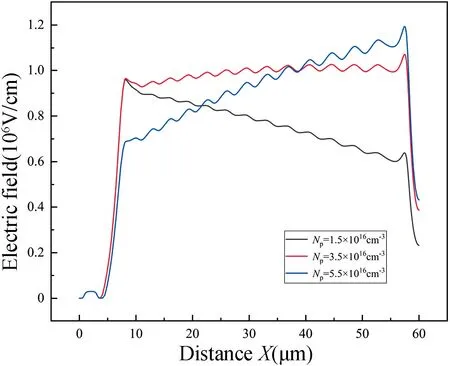
图10 漂移区内关断状态电场分布Fig.10 Off-state electric field distributions in drift region

综上所述,当NP较小时,器件从栅极端到漏极端的表面电场分布仍呈下降趋势,但漂移区和漏极端承担的电场强度相较于T-LDMOS 有所提高。随着NP的增大,场限环进一步增强对漂移区的耗尽,使得漂移区表面电场更为均匀,当漏极端与栅极端电场强度基本相同时,击穿电压达到最大。NP继续增大,靠近器件漏极端表面的电场峰值继续升高,由于电场峰和漏极端表面电场相互作用,使得漏极端表面电场不断升高,最终导致器件在漏极提前击穿,击穿电压下降,可靠性降低。所以综合考虑选择合适的NP能够有效提升器件的击穿特性和可靠性。

2.5 漂移区掺杂浓度对击穿特性的影响

漂移区的掺杂浓度对器件击穿电压有较大的影响。根据经典理论可知,漂移区掺杂浓度增大,耗尽层宽度减小,电场强度增大,当电场强度达到SiC 材料临界击穿电场时,器件发生击穿。

图11 为MR-LDMOS 不同NP对应的ND与VB的关系。由图可知,不同NP器件的VB均随着ND的增大,先增大后减小。并且随着NP增大,最高VB对应的ND也在增大。由图11 插图可知,NP分别为1.5×1016,3.5×1016和5.5×1016cm-3时,取得最高VB分别为4875,5137 和5129 V,所对应的ND分别为3.5×1015,4.5×1015和5.5×1015cm-3。并且随NP和ND的继续增大,最高击穿电压基本不变。

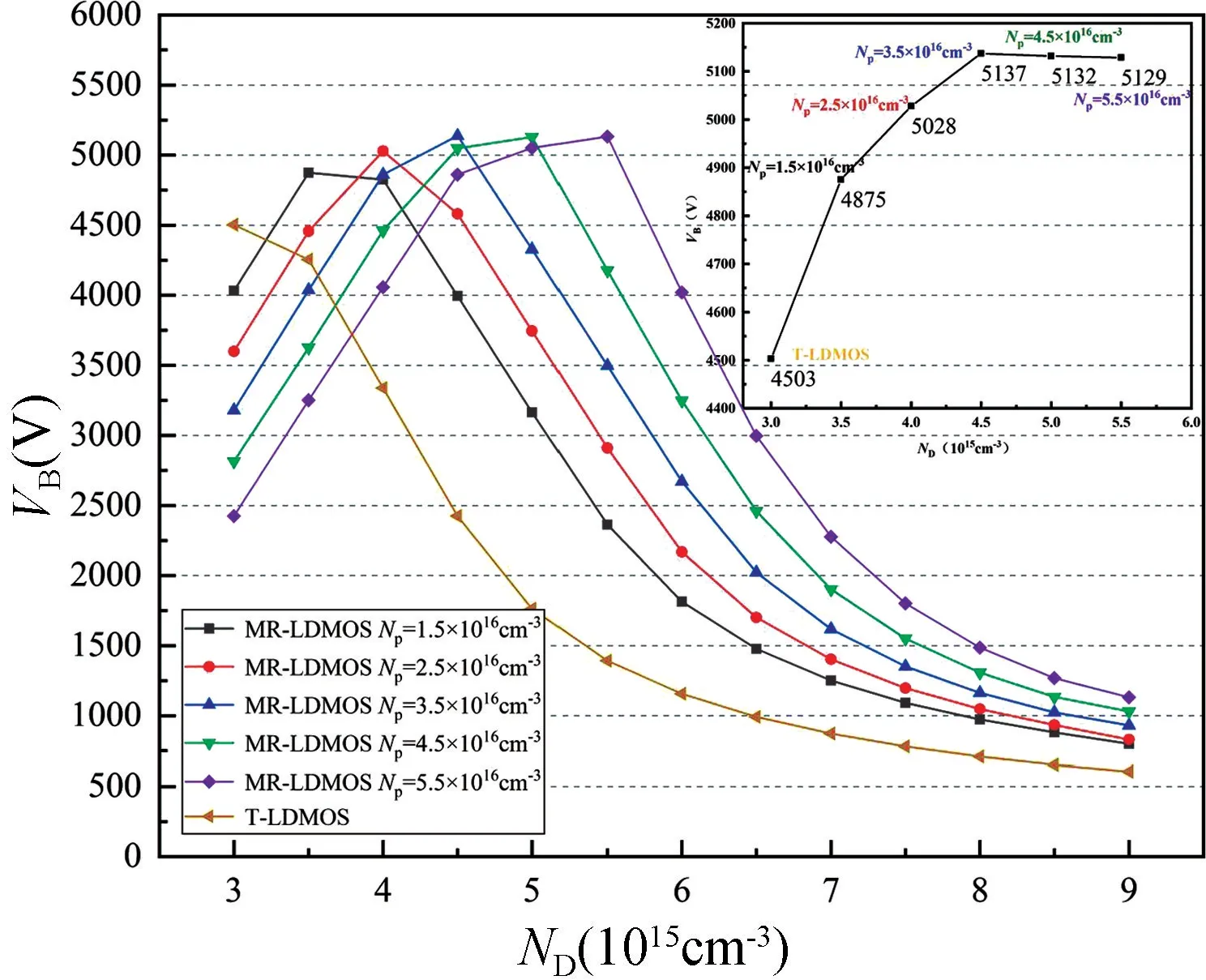
图11 不同NP对应的ND与VB的关系Fig.11 Relationship between ND and VB corresponding to different NP

为进一步分析漂移区掺杂浓度ND影响击穿电压的机理,根据图11 数据,分别取NP为1.5×1016,3.5×1016和5.5×1016cm-3,ND为4.5×1015和7.5×1015cm-3,并截取器件关态击穿时表面电场分布(沿直线AA＇),结果如图12 所示。NP一定时,随着ND从4.5×1015cm-3增至7.5×1015cm-3,漂移区承担的电场强度逐渐降低,靠近漏极端的多个场限环因基本不承担电场而失效。ND=7.5×1015cm-3时,NP为1.5×1016,3.5×1016和5.5×1016cm-3的失效场限环数量分别为7,5 和3个。即ND越大,NP越小,失效场限环数量越多。

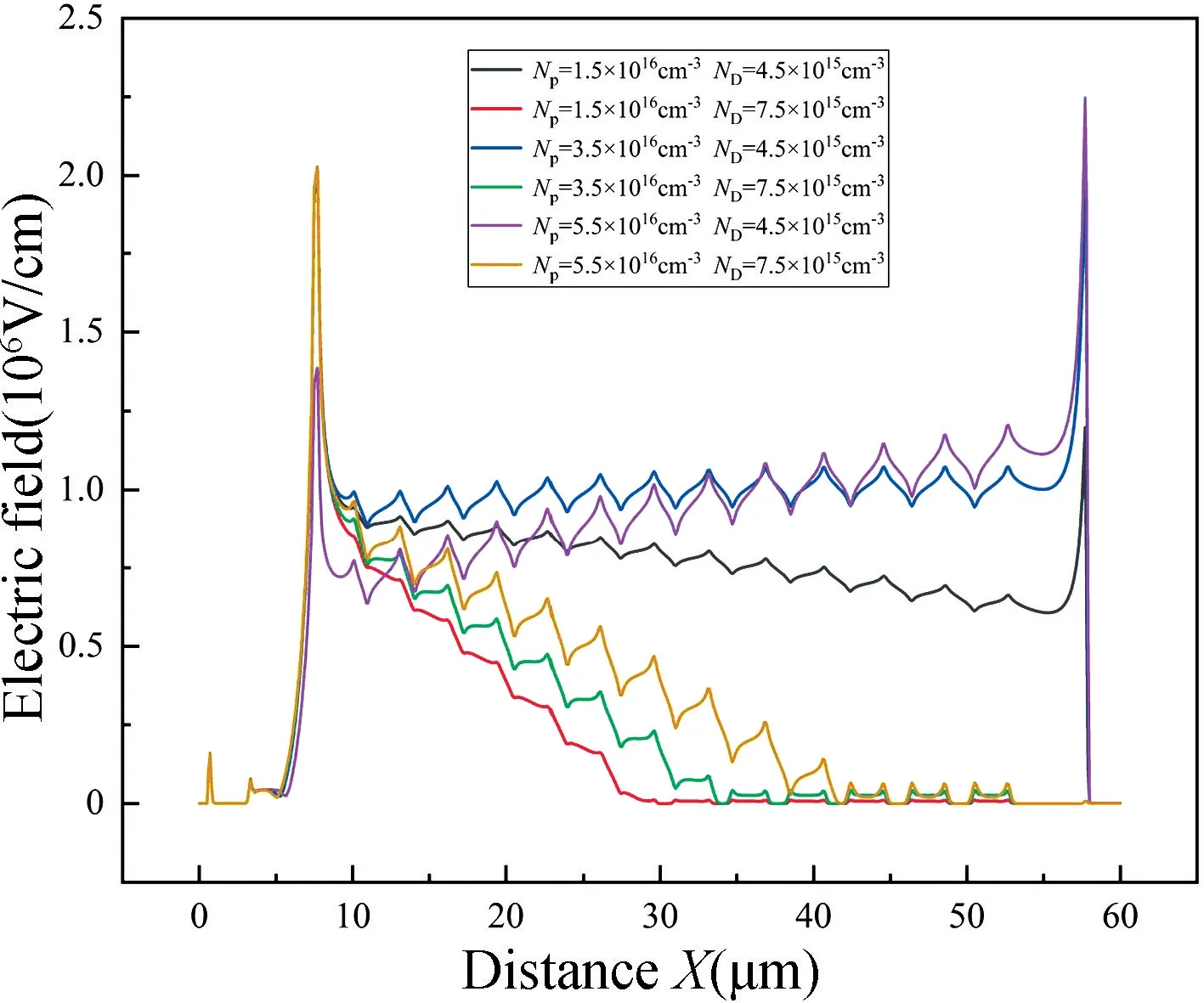
图12 不同NP对应的ND与关断状态表面电场分布的关系Fig.12 Relationship between ND and off-state surface electric field distribution corresponding to different NP

图13 为MR-LDMOS 不同Rj对应的ND与VB的关系。NP为3.5×1015cm-3,环宽为2 μm。从图中可知,随着ND的增大,不同Rj器件的VB均呈现出先增大后减小的趋势。由图13 插图可知,ND从2.5×1015cm-3增至1.1×1016cm-3,Rj分别为0.1,0.2 和0.3 μm 时,最高VB分别为4964,5137 和5132 V,对应ND分别为3.5×1015,4.5×1015和5.0×1015cm-3。随着Rj的增大,最高VB所对应的ND也在不断增大。

根据图13 数据,分别取Rj=0.2 μm 和Rj=0.3 μm,ND=4.5×1015cm-3和ND=7.5×1015cm-3,并截取器件关态击穿时表面电场分布(沿直线AA＇),结果如图14 所示。从图中可知,器件表面电场分布随漂移区掺杂浓度变化而变化。ND从4.5×1015cm-3增至7.5×1015cm-3,Rj=0.2 μm 时,第9 至第13 个场限环失效。ND增大使得P-body/N-drift 结耗尽层宽度减小,无法扩展至靠近漏极侧的场限环,导致部分场限环失效,VB下降。Rj=0.3 μm 时,由于漏极端电场强度过高,器件在漏极击穿,随着ND增大,漏极端电场强度逐渐降低,击穿点从漏极转移到栅极边缘,第12 至第13 个场限环失效。

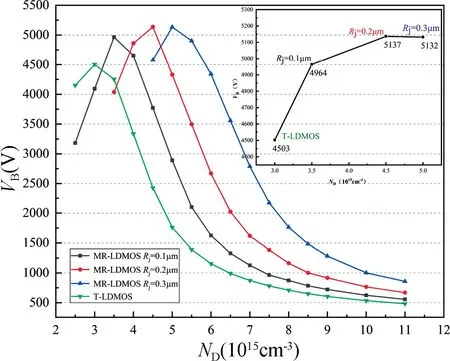
图13 不同Rj对应的ND与VB的关系Fig.13 Relationship between ND and VB corresponding to different Rj

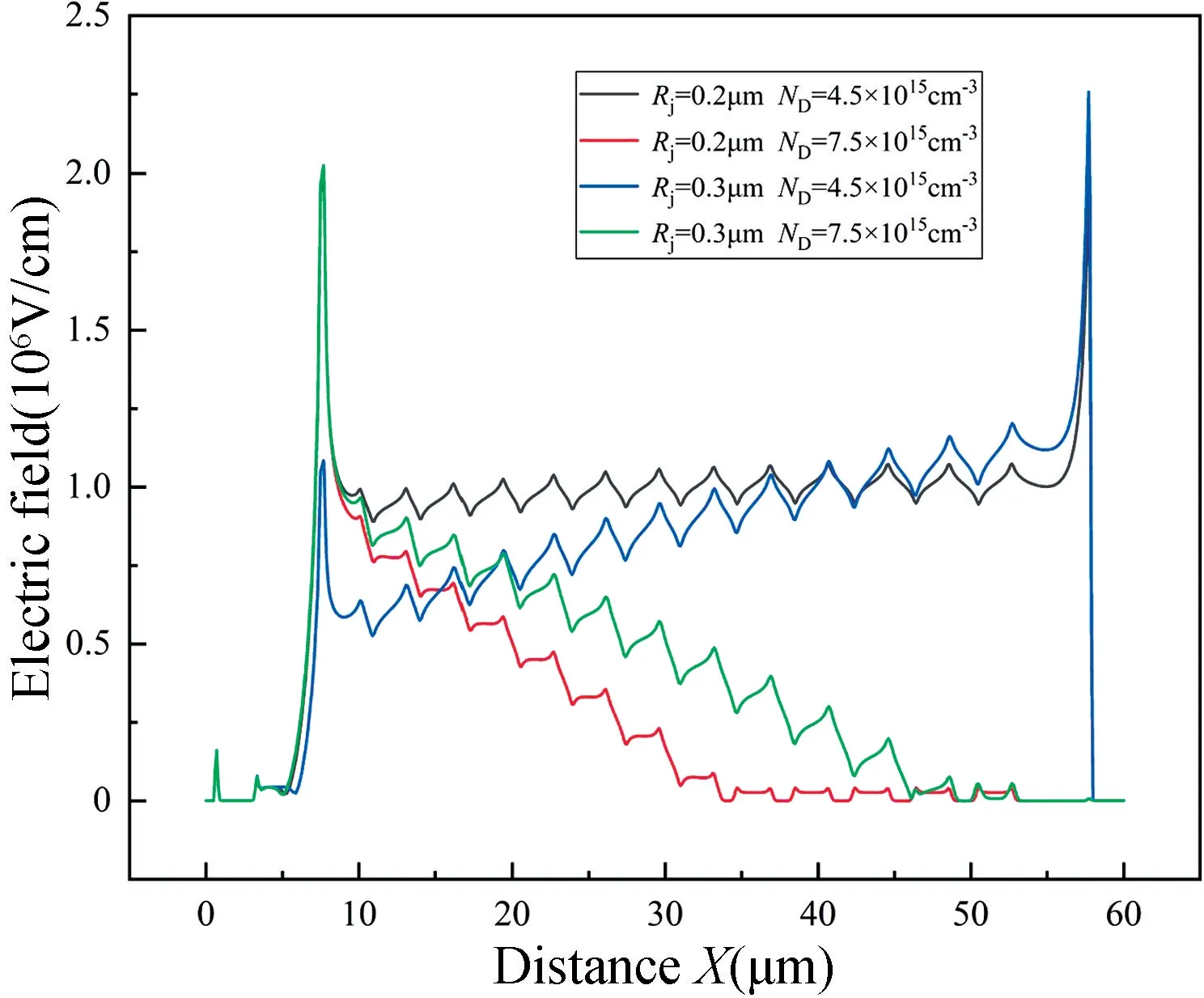
图14 不同Rj对应的ND与关断状态表面电场分布的关系Fig.14 Relationship between ND and off-state surface electric field distribution corresponding to different Rj

综上所述,当环掺杂和环结深一定时,增大漂移区掺杂浓度会抑制P-body/N-drift 结向漏极端扩展,使得部分场限环无法承担电场而失效。同时,失效场限环的数量随着漂移区掺杂浓度的增大而增大,并且当漂移区掺杂浓度一定时,失效场限环的数量随着环掺杂浓度和环结深的减小而增大。以上情况均会使得器件击穿电压下降。

3 结论

本文对具有多场限环结构的SiC LDMOS 击穿特性进行了仿真研究。探究场限环各项参数以及漂移区掺杂浓度对击穿电压的影响。分别从器件击穿特性和表面电场分布两方面进行分析。仿真结果表明: 随着场限环数量的增大,击穿电压先增大后减小。当场限环数量一定时,线性环间距设计优于等环间距设计,器件击穿电压随着环掺杂浓度的增大而先增后减。当环掺杂浓度一定时,击穿电压随环结深的增大而先增后减。当环结深一定时,击穿电压随漂移区掺杂浓度的增大而先增后减。并且随着环掺杂浓度和环结深增大,取得最高击穿电压对应的漂移区掺杂浓度增大。综上,当Rn为13,NP为3.5×1016cm-3,Rj为0.2 μm,ND为4.5×1015cm-3时,取得VB最大值5137 V(较TLDMOS 提升112.2%)。另外,由于高漂移区掺杂浓度抑制了P-body/N-drift 结的扩展,导致靠近漏极端的场限环失效,并且环掺杂浓度和环结深越小,失效的场限环数量越多。所以需要对器件结构参数进行综合分析,从而更有效地优化击穿电压,提升器件的可靠性。