基于问题情境创设培养小学生的准变量思维

高健 赖志辉 曾九龙

作者简介：高健（1999—），贵州师范大学硕士研究生，主要从事中小学数学教育研究工作。

[摘  要] 准变量思维作为沟通学生算术思维向代数思维过渡的纽带，对学生代数知识的学习起着至关重要的作用。将准变量思维科学合理地渗透到数学问题情境教学中，有利于培养学生的代数意识和数学素养，促进学生代数思维的形成与发展。

[关键词] 准变量思维;问题情境教学;代数意识

一、引言

21世纪初，贵州师范大学吕传汉教授和汪秉彝教授通过实证研究，提出“数学情境与提出问题”的教学模式，旨在培养学生的创新意识和实践能力，引起了数学教育领域巨大的反响，至今仍被中小学数学课堂教学广泛使用[1]。20世纪70年代末，教育部针对小学数学教学的特点，在其颁布的教学大纲中首次提出“适当增加代数、几何的部分内容”，并对代数教学提出了新的要求。随着学生数学认知结构的建立和形成，特别是在代数知识学习领域，学生从小学到初中乃至高中，其数学思维会在潜移默化中从小学阶段的算术思维向中学阶段的代数思维进行转变。但这种转变不是一蹴而就的，是从“低级”向“高级”逐步演变，不是绝对的“线性关系”，其间需要准变量思维进行联结，这也使得准变量思维越来越被当今的数学教育研究者和广大数学教师所重视。如何在问题情境创设中科学合理地渗透准变量思维，既是当今数学教育研究的一个热点，又是笔者长期以来持续关注和不断反思的一个问题。将准变量思维融入数学问题情境教学中，不仅有利于教师教学过程的创新，还有利于提升学生的数学思维水平，促使学生真正发现数学学习的意义和价值，进一步体会和感悟数学的数字美和符号美。

二、关于准变量思维

加拿大学者路易斯·拉弗德对代数及其小学生代数思维的发展进行了长期的深入研究，通过理论分析和实证研究，发现思维是一个“物质—想象”的动态系统，对于思维的研究应作为一个整体来进行[2]。学者徐文彬教授认为“准变量思维”的核心在于小学数学教师教算术时要间接性地向学生传授代数思维，指出准变量思维是关于“变化的数”的关系性思维[3]。学者毛新薇强调准变量思维是算术思维的“最近发展区”，算术思维作为一种程序性的“数”的运算思维，在小学阶段更为突出;代数思维作为一种关系性的“式”的运算思维，在初中阶段更为侧重[4]。从算术演变为代数，对学生而言，不仅是对数学科学认识上的一次转变，还是自身数学知识体系构建的一次重要飞跃。处于算术思维和代数思维之间的准变量思维，既是学生理解数学关系的一种新工具，又是学生数学思维认知的一种新习惯。

比如92-7+7=92，这个等式中所蕴含的代数关系与结构为m-n+n=m;如果把92和7当作单纯的两个数量进行先相减再求和得出一个值，那么这种思维就是程序性的算术思维;若是透过92、7两个数字的表面观察等式的内在结构，发现所隐含的代数关系，那么这种思维就是准变量思维。因此，在数学课堂教学中，教师应当有意识、有观念、有操作地发展学生的准变量思维，借助问题情境渗透准变量思维：如图1所示，一方面使学生感受數学与生活的密切联系、积累数学活动经验;另一方面转变学生思考问题的方式，顺利向代数思维进行过渡。

三、准变量思维在问题情境中的创设

1. 融合生活情境，渗透准变量思维

袁智强博士说：“与数学相比，数学教育是一门非常年轻的学科。”[5]数学具有高度的抽象性和严密的逻辑性，对于小学阶段的学生而言，其思维正处于由具体形象思维到抽象逻辑思维过渡的阶段，需要以大量的感性经验做支撑。因此，在数学教学中，准变量思维的渗透应当注重联系学生的日常生活实际和个人成长经验，让学生的思维经历“数学化”的过程，引导学生从自己的生活经验出发，将数学知识的学习和日常生活经历有机结合，从而使感性经验上升为理性认识。

在小学多位数与多位数的减法运算中，如果教师只是单纯地出示这样一个计算“343-99”，基于学生以前的学习经验，大部分学生会想到用竖式计算得到答案，但这只是算术中程序性思维的重复展现。若是合理地进行问题情境创设，将准变量思维有机融合到数学问题情境中，不仅有利于学生深刻体会现实生活中的数学，而且便于培养学生的准变量思维。比如，在真实的数学课堂教学中教师可以这样进行设计：

（1）创设数学问题情境：小强作为班级的劳动委员，利用剩余的班费343元为班级购买了新的劳动工具，花费了99元，还剩下多少班费？

（2）组织学生进行探讨。

（3）请小组代表分享讨论的结果。预设有两种结果：第一种，学生列出等式后通过竖式进行计算;第二种，学生列出等式“343-99”进行变形计算，得到“343-99=343-100+1=243+1=244”，以此组织学生讨论为什么要这样变形？重点讨论为什么“加1”？

（4）采取简便方法计算：676-197，578-499。

（5）进行简便计算规律的总结。

在真实的数学教学中，可能部分教师会认为一个多位数与多位数的减法计算，只要学生会用竖式计算得出正确结果就可以，设置问题情境进行互相探讨、总结规律未免有些小题大做。其实不然，如果只是单一地给出算式让学生计算得出结果，那么学生的学习仅止步于“为计算而计算”的层面，教师向学生渗透准变量思维就难上加难了。创设问题情境，让学生参与情境之中获得身临其境的感觉，更容易使学生获得实际经验和感悟数学的现实价值。上述情境学生体验之后，会深刻体会到：假如自己去商场买劳动工具花费99元，付给售货员100元，售货员找回自己1元。有了这种体会之后，学生就更容易理解“加1”的缘由，教师便可顺水推舟地向学生强调简便算法的原理，最终得出简便算法的规律：一个多位数减去略小于整百、整千乃至整万的数，可以先减去整百、整千乃至整万，再加上多减的数就是最终的结果。可见，在培养学生准变量思维的教学中教师科学合理地创设问题情境，既可以促进学生数学思维的发展，又可以更新学生的认知结构和数学理解。

2. 引入故事情境，丰富准变量思维

数学教学中教师以故事引入教学主题和知识内容，不但可以帮助学生快速进入知识学习的氛围中，而且可以使学生认识到数学应用的广泛性和存在的普遍性。在故事情境中培养学生的准变量思维，既有利于引发学生的猜想和推理能力，又有利于提高课堂的趣味性，激发学生的学习兴趣。特别是对于小学阶段的学生，其认知结构和数学思维正处于萌芽期，教师在课堂教学中适当地引入故事案例，既符合小学生的心理发展规律，又有利于学生的认知建构和能力发展。比如，在教学多个有限项求和计算时，教师可以德国数学家“高斯”的故事进行情境引入。

（1）创设故事情境：被称为“数学王子”的高斯，小时候和班里其他同学一样调皮，他的数学老师为了让班里同学安静下来，于是就在黑板上列出一道很长的算式1+2+3+4+…+100，并让他们在一个小时内算出答案，这该如何计算呢？

（2）组织学生进行同桌讨论：2+4+6+8+…+100;（10+11+12+13+…+50）-（5+6+7+8+…+45）。

（3）学生讨论后请同学代表发言。假设有两种情况：第一种，学生在草稿纸上逐项进行计算求出结果;第二种，学生讨论出简便算法，通过前后对称项相加的方式计算，即用“高斯算法”求出结果。教师要抓住机会组织学生探究此种计算方法，重点讨论为什么要将前后对称项两两结合？

（4）采取简便算法计算。

（5）进行简便计算规律的总结。

以“高斯算式”的故事引入，以历史故事情境为切入点，在观察、猜想、探究、归纳、计算求解等过程中向学生渗透准变量思维。高斯计算等式的故事在数学教育界广为流传且具有典型意义，教师将其合理融合在小学高年级算法教学中，对学生从算术思维向代数思维转变具有积极意义。

基于上述问题情境，首先，学生身处此算法具体情境当中，大部分同学可能会出现一时难以解决、思维混乱、难以下笔的情况。经过一番观察之后，有的学生会逐项一步步进行计算;有的学生通过观察探究之后，发现这一等式中的每一对前后对称项之和都相等，只需要用“对数×每一对两个数之和”即可求出结果;其次，教师因势利导，和学生一起讨论比较这两种计算方法，既要使学生理解高斯算法的内涵和原理，又要使学生深刻感知此算法的简便性和可操作性，便于学生日后进行应用和拓展;最后，教师与学生一起总结算法规律，促进学生对该算法的理解和掌握，在算法学习中潜移默化地渗透准变量思维。

3. 嵌入虚拟情境，培养准变量思维

数学教学中虚拟情境的创设是学生掌握知识和发展能力的重要载体，这种情境具有一定的抽象性和非具体性，学生在这种情境中通过观察、猜测、归纳、验证与证明等操作活动，将新旧知识进行有机整合，进而形成有意义的学习[6]。教师在虚拟情境中向学生渗透准变量思维，不仅有利于培养学生的动手操作能力，而且有助于提高学生的问题探究能力，使学生在情境中提升思维水平、在探究中领悟数学思想。比如：

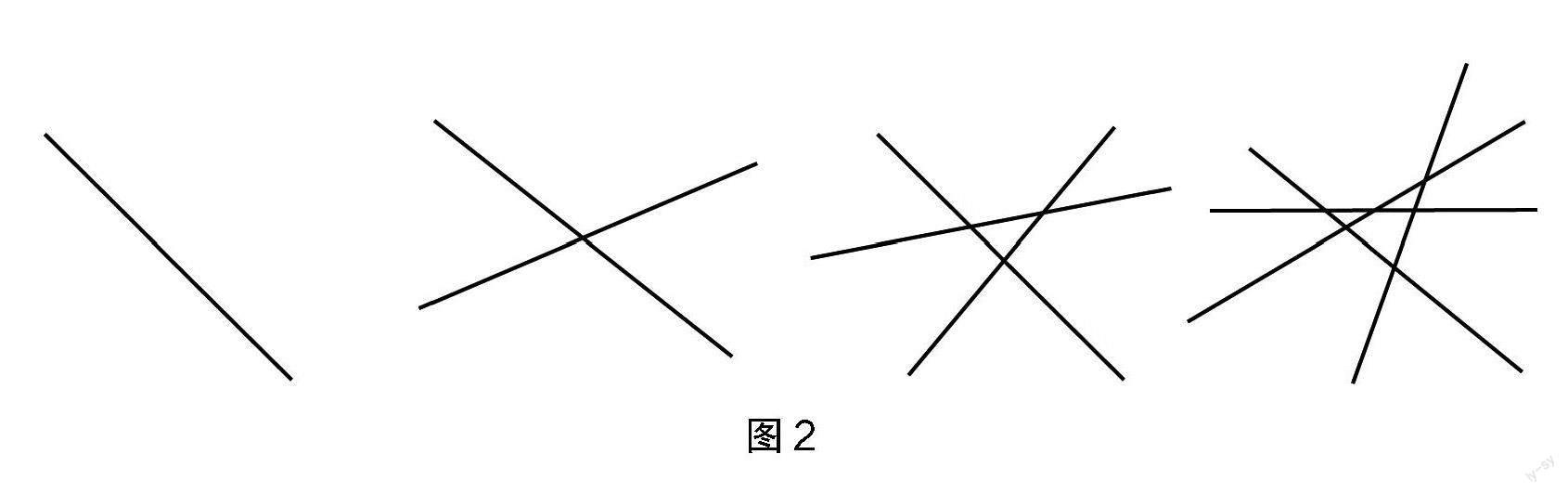
（1）创设虚拟情境：一个人在一片平整的土地上种蔬菜，需要将土地区域进行划分，他发现在同一个平面上，1条直线可以将该平面分成2个区域，2条互不平行的直线相交可以将平面分为4个区域，那么3条互不平行的直线可以分出多少个区域？4条？5条？20条？n条呢？（不用写出具体表达式，用y1，y2，y3，…，yn表示即可）

（2）直观感知：分别画出前几项直线条数得出区域数值，此时学生仍处于程序性的算术思维，如1条直线得到2个区域，2条直线得到4个区域，3条直线得到7个区域，4条直线得到11个区域，如图2所示。

（3）渗透关系思维：通过画图以直观的方式引导学生列出等式，比如：y1=2，y2=4，y3=7，y4=11，y5=16等。

（4）强化准变量思维：组织学生观察图形，可以发现：每增加1条互不平行的直线，则新增直线与原有直线的交点个数为原有直线的个数，新增区域为总直线的个数;为此，可以得到从第二个图形开始，每个图形中互不平行的直线划分的区域为“前一个图形的区域数+该图形的直线个数”，进而启发学生写出准变量表达式：y1=2，y2=y1+2，y3=y2+3，y4=y3+4，y5=y4+5;进而得到20条互不平行的直线相交时，划分的区域数可以表示为y20=y19+20;n条直线时，区域数可以表示为yn=yn-1+n（n为非零自然数）。

上述题目通过创设虚拟情境，引导学生探索直线与直线、直线与平面区域之间的特点和关系，发现直线个数与相邻项数之间的内在联系，在规律探究中引入符号语言、渗透准变量思想。当然，上述所举问题，有些学生会陷入无止境的画图泥潭中，在一条直线的基础上，逐次增加直线、数交点、数区域个数，但随着线条数目的增加，不仅导致学生操作难度越来越大，而且容易使学生陷入狭窄的思维泥潭，丧失数学探究的兴趣。因此，基于数学虚拟情境进行准变量思维渗透时，教师应该注意两个方面：第一，数学知识彼此之间是有联系的，进行准变量思维渗透时，题目筛选和探究问题并不仅局限于算术领域，特别是几何题目中的规律探索问题，也是渗透学生准变量思维的一个有效选择;第二，准变量表达式的呈现以及准变量思维的渗透，大多数学生会借助归纳的推理方法，因此教师在进行思维培养时应当注重引导学生观察和发现，在发现中寻找数学的趣味性和科学性，在探究中领悟从“特殊到一般”的数学归纳思想，进而提高学生的数学学力和转变学生的数学思维。

四、准变量表达式在问题情境中创设的意义

1. 加强认知建構，提升数学思维

准变量表达式作为准变量思维的一种表现形式，成为学生从算术思维向代数思维过渡的有效载体。在“问题情境教学模式”火热兴起的教育改革时代，教师将准变量思维科学合理地渗透到问题情境教学中，一方面有助于学生数学思维能力的有效增强，另一方面对学生代数思维水平的形成与发展具有积极的建构意义。特别是小学阶段的学生由于自身发展能力的局限性和所学知识的特殊性，更倾向于算术思维进行数学问题的解决。进入中学阶段之后，数学知识的高度抽象性和逻辑性需要学生具备“代数的眼光”重新认识数学，这就导致很多学生在短时间内难以适应中学数学知识的学习，成为掣肘学生数学兴趣培养和数学能力发展的瓶颈。因此，准变量思维作为学生代数思维形成的中介，在问题情境教学中进行科学合理的渗透是必要的。

2. 简化探究操作，促进问题解决

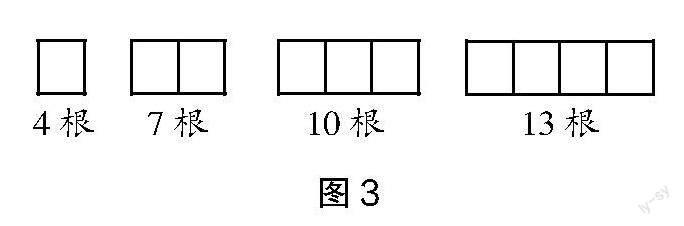
数学学科的学习并不单是知识的学习，更重要的是学生在学习过程中获得的学习经验、生活技能、思维品质以及人生哲理。准变量思维作为学生思维能力形成和发展的重要阶段，既是学生能力提升的关键一步，又在教师课堂教学过程中起着重要的支撑作用。特别是在问题情境教学环节，学生融入数学情境之后，随着对情境的深入理解和对问题的进一步感知，仅停留在算术思维水平上难以对问题解决进行全方位多角度的认识和处理。比如，用“火柴棒逐个摆正方形”问题，要求正方形从左到右依次进行排列，如图3所示。

1个正方形需要4根火柴棒，2个正方形需要7根火柴棒，3个正方形需要10根，4个正方形需要13根，那么10个正方形需要多少根？30个正方形呢？基于此类情境问题，如果学生仅停留在算术思维层面，那么大部分学生的操作方法就是“拼一拼、数一数”，从第1个正方形依次数数，直到第10个正方形乃至第30个正方形，这种操作方法虽然也能得到最终答案，但是过于烦琐复杂;如果在此问题中教师适当进行引导，向学生渗透准变量思维，以准变量表达式（即yn=3n+1，n为非零自然数）为切入点启发学生进行求解，将“10、30”分别代入准变量表达式中，则更加简捷易操作。可见，在问题情境教学中，适当引入准变量表达式、向学生渗透准变量思维既有利于增强学生解决问题的能力，又便于教师快速传授数学知识。

3. 弥合认知偏差，提高教学水平

问题情境教学模式作为增强学生数学思维能力和培养学生数学核心素养的有效方式，已广泛应用于中小学的课堂教学中。而数学教师的教学认知偏差，会导致数学问题情境创设中“重‘虚拟情境而轻‘真实情境、重‘横向数学化而轻‘纵向数学化、重学生‘自主探究而轻教师‘启发引导”的现象层出不穷[7]。如果在问题情境中适当向学生渗透准变量思维，在问题解决中科学引入准变量表达式，那么对学生的认知能力和思维发展具有积极的建构意义。准变量表达式以其符号化、简洁性、易操作性存在于学生的“最近发展区”，正是准变量表达式的简洁性和独特性，使得教师在“问题情境教学与学生思维融合中”必须平衡情境的真实性与虚拟性、数学化的横向性与纵向性、教师的启发引导性和学生的自主探究性。因此，将准变量思维渗透到问题情境教学中，既有助于强化学生的数学思维认知，又有利于弥合教师教学的认知偏差。

总之，准变量思维在问题情境教学中的渗透对学生的数学发展具有积极的启蒙作用，教师应在问题情境教学中适当引入准变量表达式，积极捕捉适合学生思维发展的感性材料，在情境中隐含准变量思维、在问题中呈现准变量表达式、在探究中引入代数的关系与结构，为学生从算术思维向代数思维的顺利过渡和有效发展保驾护航。

参考文献：

[1] 吕传汉，汪秉彝. 论中小学“数学情境与提出问题”的数学学习[J]. 数学教育学报，2001（04）：9-14.

[2] 张丹. 如何理解和发展代数思维——读《早期代数思维的认识论、符号学及发展问题》有感（上）[J]. 小学教学（数学版），2012（11）：5-7.

[3] 徐文彬. 如何在算术教学中也教授代数思维[J]. 江苏教育，2013（33）：16-17.

[4] 毛新薇. 准变量思维：赋予学生代数思维生長的力量[J]. 江苏教育，2014（05）：40-41.

[5] 鲍建生，徐斌艳. 数学教育研究导引（二）[M].南京：江苏教育出版社，2013.

[6] 张岚. 数学问题情境的三种类型[C].新世界中国教育发展论坛：第二卷，2007.

[7] 夏小刚，张晶. 从问题情境创设看数学教学的认知偏差[J]. 湖北教育（教育教学），2022（02）：31-33.