基于神经网络和粒子群算法的永磁同步电机运行与振动性能优化

胡文韬，李 华，郑 东，华春蓉，沈思思

(1 西南交通大学 机械工程学院，成都 610031；2 山东省东营市胜利油田石油化工总厂中心化验室，东营 257000；3.国家知识产权局专利局专利审查协作四川中心，成都 610014)

0 引 言

永磁同步电机是目前新能源汽车驱动电机的主要发展方向[1]。对于电机工程师来说，电机的高效率、高转矩、高转速一直是追求的目标；另一方面作为传统汽车噪声主要声源的发动机被替代，纯电动汽车的高频电机噪声成为直接影响其声品质和乘坐舒适性能的重要因素[2-3]。本文基于最优化算法对电机结构参数进行优化，在不影响电机驱动性能的同时降低振动。

文献[4]基于局部电磁力和整体力的关系，使用优化电机参数的方法显著降低了电机的转矩脉动，同时优化了电机的径向电磁力。文献[5]采用解析方法和有限元分析方法，估计了考虑开槽效应永磁同步电动机的转矩脉动、齿槽转矩和径向力密度等振动特性，并通过实验进行验证。文献[6]用Lyapunov直接法研究了多个平衡点及其稳定性，并分析了电动汽车用永磁同步电动机转子的自由振动和频率特性，得出结论：响应幅值限制在两个平衡点的幅值范围内，在平衡点连续体附近，系统几乎不提供抗弯曲能力，因此外部干扰容易导致稳定性损失。文献[7]基于Kriging方法建立了直线电机的映射模型，并使用多目标全局优化方法对电机进行优化设计，在大幅减少计算资源消耗的同时进一步提升了计算准确度。

大量文献只对电机的单一性能进行研究和优化，而运行性能与振动性能会呈现此消彼长的特点，因此需综合分析电机的运行和振动性能。作者前期针对丰田Prius永磁同步驱动电机进行了运行和振动特性综合分析，结果表明：电机输出功率较高，但其转矩脉动约27.12%；2 400 Hz电磁激振力较大，且与电机定子模态三阶固有频率接近，易引起较大振动。针对这一问题，本文将在前期研究的基础上，提出同时考虑运行和振动性能的综合优化方法，并对该电机进行多目标优化。

1 电机结构参数对其性能及振动影响分析

在电机学中，电机电磁场的仿真计算从数学上分析，属于求解若干偏微分方程。而有限元法作为一种基于变分原理和离散化进行求解近似值的方法，不仅具有灵活通用的特点，还可以有效处理非线性媒质特性(如铁饱和特性)和涡流问题[8]，成为目前工程技术领域的数值计算中最常用的一种方法[9]。

麦克斯韦方程是驱动电机电磁场理论的基础。在使用Maxwell方程计算电磁场时，通常使用Maxwell方程组的积分形式，从而将计算空间中电磁场媒质的突变考虑在内，如下式：

式中：场量B、E、D、H之间的关系由媒质的特性决定。

本文基于有限元法对内置V型永磁体转子链路结构的电机永磁体厚度H、隔磁桥间距wrib、气隙长度l、定子槽口宽度Bso(如图1所示)等进行优化，并对有限元仿真结果进行分析，分析这些参数与电机驱动性能及振动性能的拟合关系。

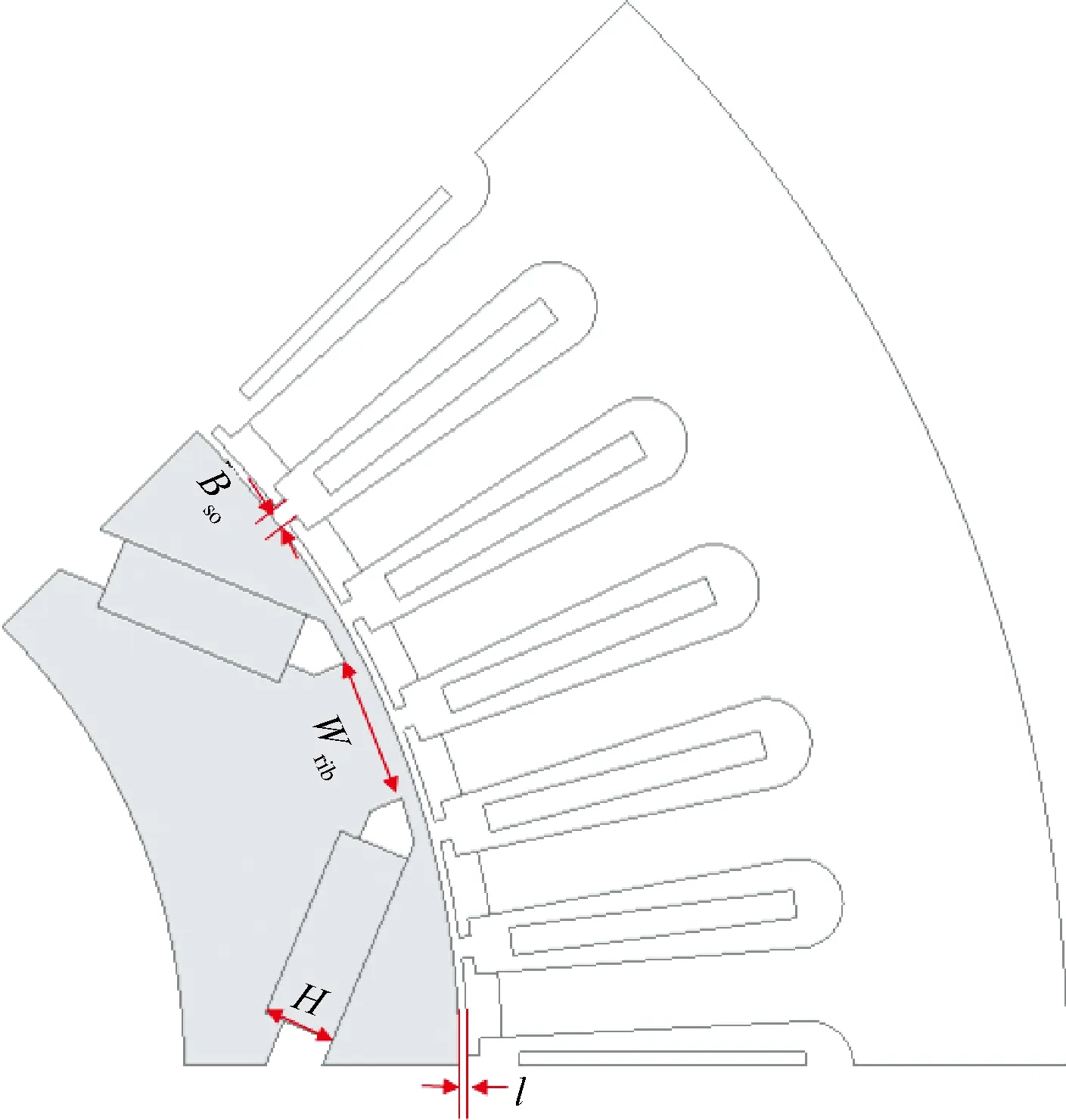
图1 本文选择变量示意图

1.1 气隙长度l

气隙是永磁同步电机最重要的、进行电能和机械能的转换场所，同时也是电机内部磁场分布最为复杂的部分，对电机各项性能表现起到关键作用。减小气隙长度会增大电机的转矩脉动，同时可以有效提升电机永磁体的使用率，但会加剧电机的振动噪声；而增大气隙长度会导致磁路磁阻大幅增大，减小气隙磁密的同时增大磁漏，从而导致电机成本升高并且降低了永磁体的利用率。本文主要仿真计算了气隙长度为0.2 mm～1.8 mm范围内时，其对电机驱动与振动性能的影响趋势。

如图2所示，根据电机理论，气隙增大，永磁同步电机的磁路磁阻增大，输出转矩减小；进一步分析可以发现，气隙磁密谐波畸变率会随着气隙长度的减小而不断增大，进而导致电机转矩脉动也随着气隙长度的减小而不断增大。如图3所示，气隙长度的增大会使得径向电磁力的主要频率谐波分量随之减小。综上，增大气隙长度有助于改善电机的振动噪声，但会降低电机的驱动转矩。

图2 气隙长度l对电机输出转矩、转矩波动的映射曲线

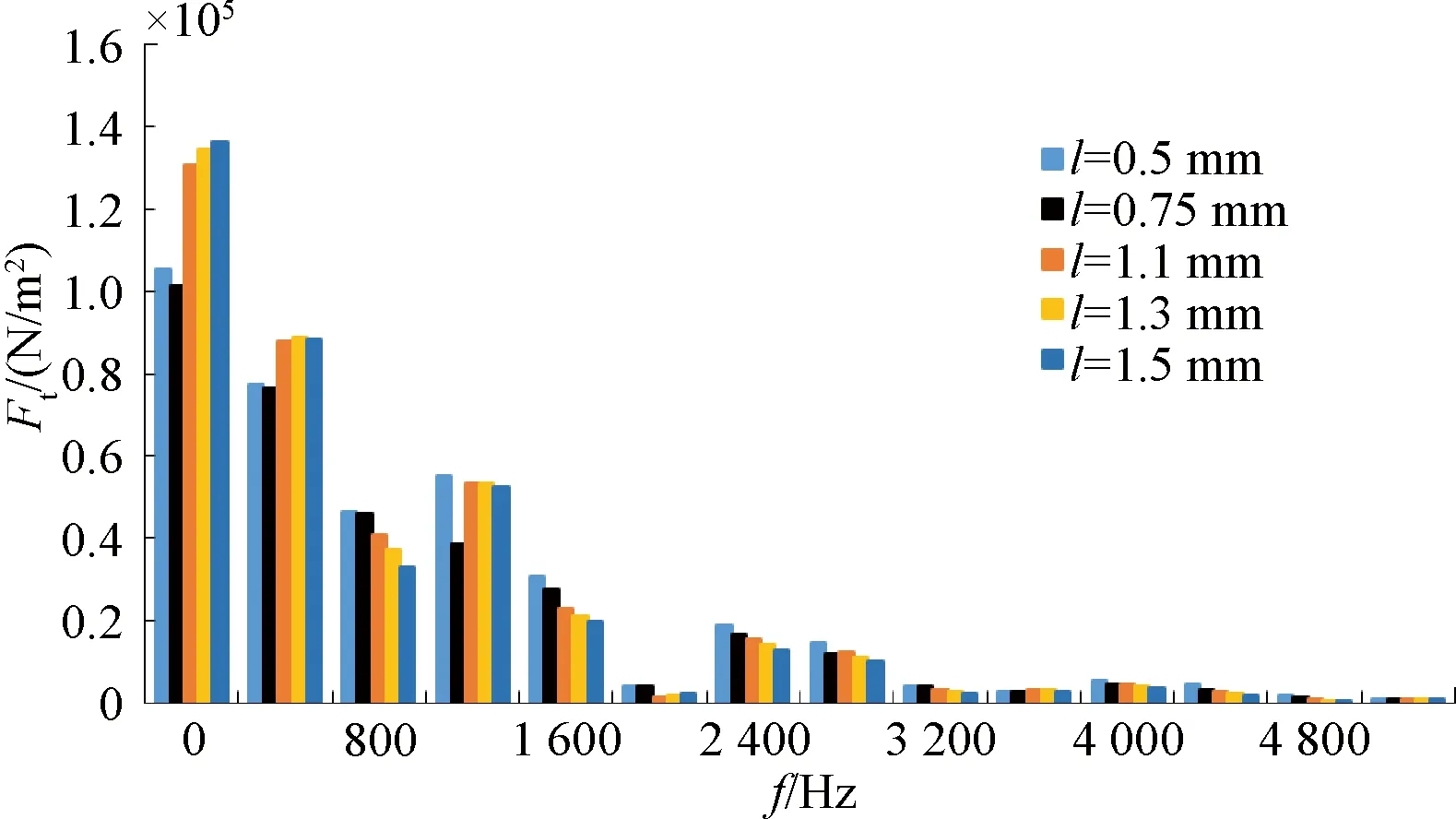
图3 气隙长度对径向电磁力的影响趋势柱状图

1.2 永磁体厚度H

永磁体是永磁同步电机中产生永磁磁场，从而与电枢磁场相互作用产生转矩的重要部分，决定了整体的性能和效率，也是电机成本的主要组成部分之一[10]。如果增大永磁体厚度，会增大电机的空载反电动势，进而降低电机的弱磁性能；如果减小永磁体厚度，则会降低电机气隙处的磁场强度，减弱电能和机械能的能量转换能力，使得电机的效率降低。因此，本文针对不同的永磁体厚度进行仿真计算，结果如图4、图5所示。

图4 输出转矩、转矩波动随永磁体厚度的映射曲线

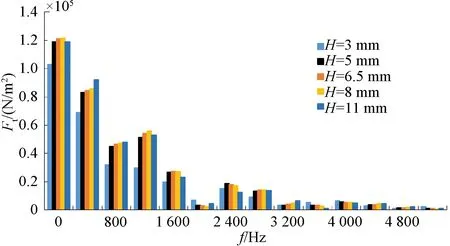
图5 径向电磁力随永磁体厚度的柱状图

由图4、图5可以看出，输出转矩随着永磁体厚度的增加而增大，在5 mm之后增加缓慢并趋近于饱和；转矩脉动在永磁体厚度为4.6 mm时为最小，波动值为23.1%，并随着永磁体厚度的增加，先减小后增大再减小。径向电磁力在400 Hz频率分量处受H变化的影响较为明显，其余频率分量处基本不受H变化的影响或变化的趋势较小。

1.3 隔磁桥间距wrib

将转子冲片连接成整体并保证具有较强刚度就构成了隔磁桥。本文主要计算了电机在恒定工作状态下隔磁桥间距对电机性能的影响，结果如图6、图7所示。

图6 输出转矩、转矩脉动随隔磁桥间距的映射曲线

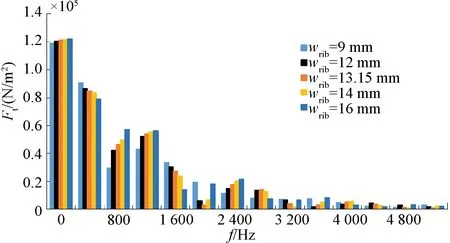
图7 径向电磁力随气隙长度的柱状图

由图6可以看出，隔磁桥间距主要对电机的输出转矩和转矩脉动影响较大，且可以发现电机的输出转矩和转矩脉动有相同的变化趋势。电机振动性能(即转矩脉动)最优时其驱动性能(即输出转矩)最差，反之亦然。同时由图7可以看出，隔磁桥间距减小时，800 Hz、1 200 Hz和2 400 Hz处的径向电磁力主要谐波分量的幅值也随之而减小。

1.4 定子槽口宽度Bso

槽口宽度是电枢尺寸的重要参数，会直接影响气隙磁阻的变化，是与永磁体磁场作用产生输出转矩和转矩脉动的场所。本文基于有限元方法，计算并分析不同大小的定子槽口对永磁同步电机性能的影响。

由图8可以看出，输出转矩会与槽口宽度以相同的趋势进行变化，这主要是由于槽口宽度变化会导致附近的磁导变化，进而导致气隙磁密幅值变化，并最终引起输出转矩以相同的变化趋势变化；而转矩脉动与定子槽口宽度有着相同的变化趋势，这主要是因为永磁同步电机定子槽开口会直接产生电机的转矩脉动。如图9所示，径向电磁力幅值整体随槽口宽度的增大而增大，可以通过适当减小槽口宽度来优化电机的振动噪声。

图8 输出转矩、转矩脉动与定子槽口宽度的映射曲线

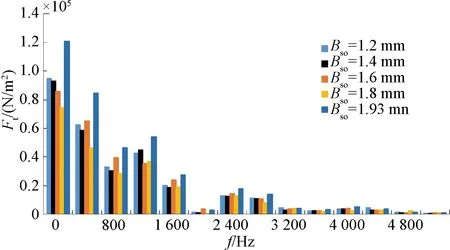
图9 径向电磁力与定子槽口宽度的柱状图

2 神经网络建立与多目标优化

通过上文基于有限元方法的仿真和分析可以发现，电机的结构参数与电机的驱动和振动性能具有较强的相关性。而使用粒子群优化算法进行多目标优化的前提是获得优化对象的优化变量和优化目标之间的映射关系模型，因此本文建立神经网络来实现电机参数到电机性能的映射。

2.1 建立驱动电机BP神经网络模型

神经网络凭借其强大的拟合和学习能力，在学界被广泛使用于解决复杂模型的非线性拟合问题。BP神经网络是通过正向和反向传递相结合的方式进行拟合和调参的多层前馈神经网络。在该网络的训练过程中，原始数据首先从输入层传入并经过中间层逐层计算后通过输出层传出，将与期望结果的误差进行反向传播，基于梯度下降的方法逐层调整各个神经元的权值和阈值，通过不断训练和学习确定最接近预期输出的网络。其训练过程如下式：

wjk=wjk+ηHjek

bk=bk+ek

本文将电机气隙长度、永磁体厚度等参数作为输入变量，输出转矩、转矩脉动、电磁力主要频率幅值等电机性能参数为输出变量，建立结构为4-15-4的单隐含层BP神经网络[11-12]。将神经网络的迭代次数设置为15 000，动态因子设置为0.9，学习速率设置为0.1。

通过设置预测数据集绘制模型拟合的误差曲线，分析可得：对于拟合对象中驱动转矩拟合结果的平均相对误差为0.7%，相对最大差值小于2%；对转矩脉动的拟合结果平均相对误差为2.04%，相对最大差值小于2；对于径向电磁力的拟合结果进行分析可以发现，1 200 Hz处拟合结果的平均相对误差为4.33%，相对最大差值小于15%；2 400 Hz处拟合结果的平均相对误差为3.86%，相对最大差值小于1%。由此验证了BP神经网络对电机相关性能预测的准确性，为下文进一步进行参数的多目标优化打好了基础。

2.2 基于多目标粒子群优化算法的驱动电机性能优化

多目标优化的优化变量选择为上文分析的电机主要结构参数，选择电机输出转矩Te、转矩脉动K、1 200 Hz径向电磁力幅值F1 200、2 400 Hz径向电磁力幅值F2 400作为优化目标，利用多目标粒子群优化算法对这些影响因素在偏差范围内进行寻优，得到边界范围内的最佳值[13]。优化变量4个因素的边界约束如下：

对于驱动电机来说，驱动性能和振动性能存在冲突，无法通过优化设计使得两个性能同时达到理论最优，只能获得非劣意义上的最优解。本文优化目标为保证电机输出转矩和转矩脉动在原始工况下的约束条件内，同时尽可能降低1 200 Hz和2 400 Hz径向电磁力幅值。

(1)

通过采用加权法来处理电机性能和径向电磁力优化问题，w1、w2、w3、w4为权值，分别为0.2、0.1、0.4、0.3。其统一目标函数表示如下：

(2)

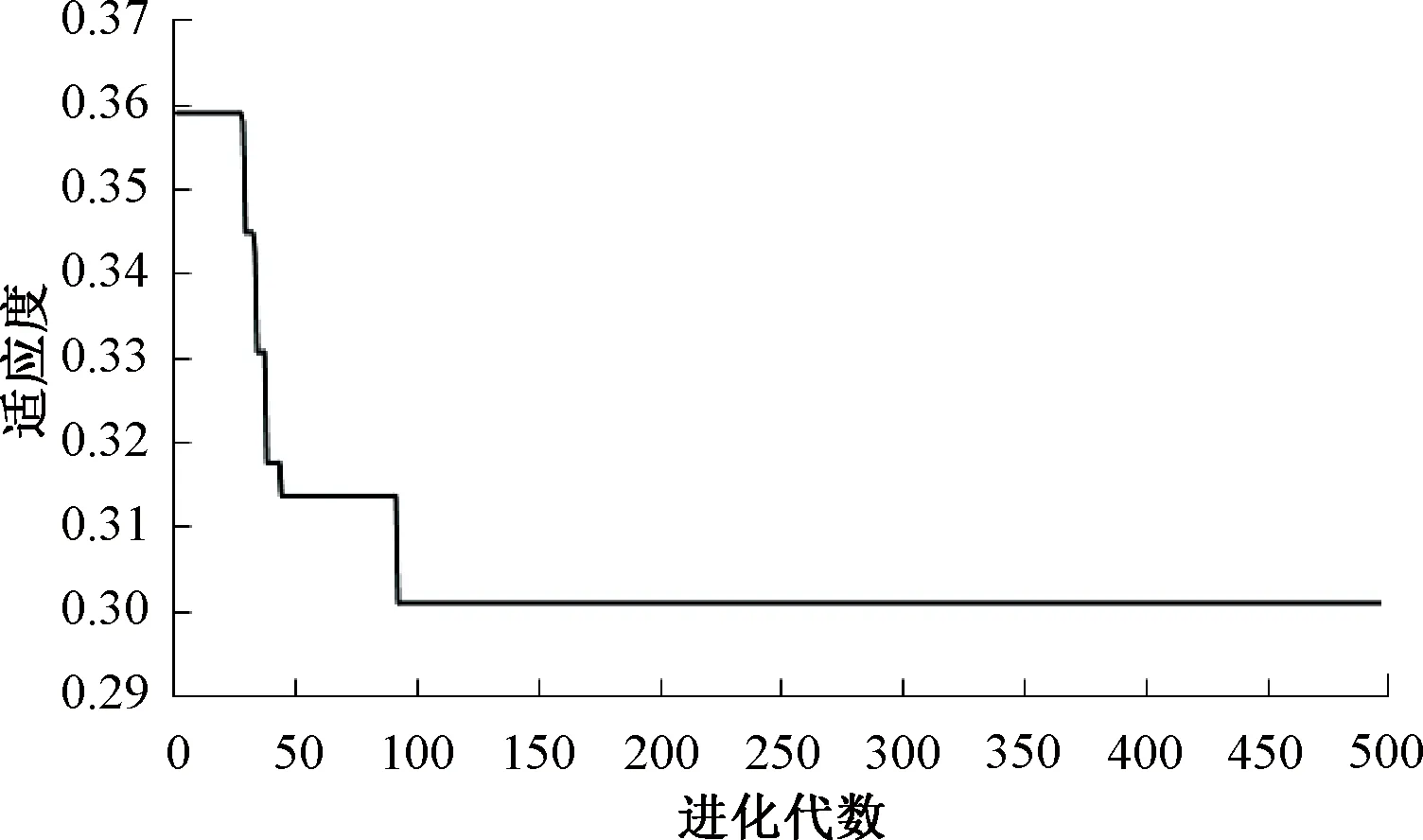
图10 多目标粒子群优化算法适应度曲线

将粒子群算法的种群规模、算法迭代次数及学习因子等参数分别设置为80、500和1.49后，基于该算法进行适应度曲线分析，如图10所示。通过图10可以看出，基于约束法和加权法的粒子群算法得到了较好的收敛效果，在g=0.301 1时，适应度函数取得最小值，此时得到的电机结构参数如表1所示。

表1 样机与优化电机结构参数对比

3 优化电机的性能和振动分析

采用数值模拟方法对优化后的电机与原始样机的运行与振动性能进行计算，并进行对比分析。

图11给出了优化电机与原始样机输出转矩的计算结果。优化电机的输出转矩最大值提高了约4 N·m，且电机转矩脉动降低了49%。可见,优化电机的运行性能有一定程度的改善。

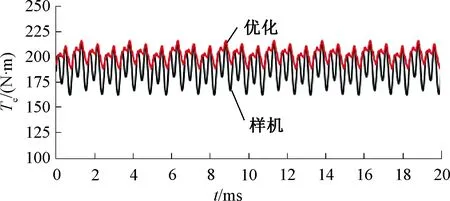
图11 电机输出转矩对比图

图12对比了优化电机与样机各个频率径向电磁力计算值。由此可见，优化电机的各主要频率所对应的径向电磁力幅值降幅较为明显。本文主要的优化目标是在保证驱动性能的基础上优化径向电磁力在主要频率分量(1 200 Hz和2 400 Hz)处的幅值，通过分析可以发现，径向电磁力幅值经过优化后整体降幅较为明显，1 200 Hz处分量幅值降幅为35%；2 400 Hz处分量幅值降幅为64.3%。

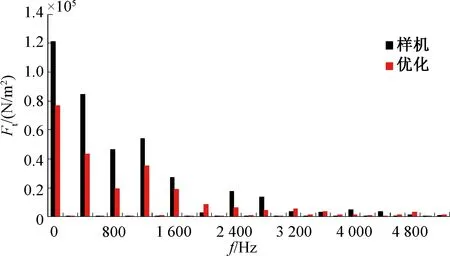
图12 电机径向电磁力对比图

将上文中多目标优化后计算得到的引起电机振动的电磁力波作为激励加载到电机的定子壳体三维有限元模型中，建立磁-固耦合模型对电机的定子部分进行谐响应分析，仿真得到电机定子铁心外表面X、Y向的振动位移频谱图，并与原始样机进行对比，如图13和图14所示。

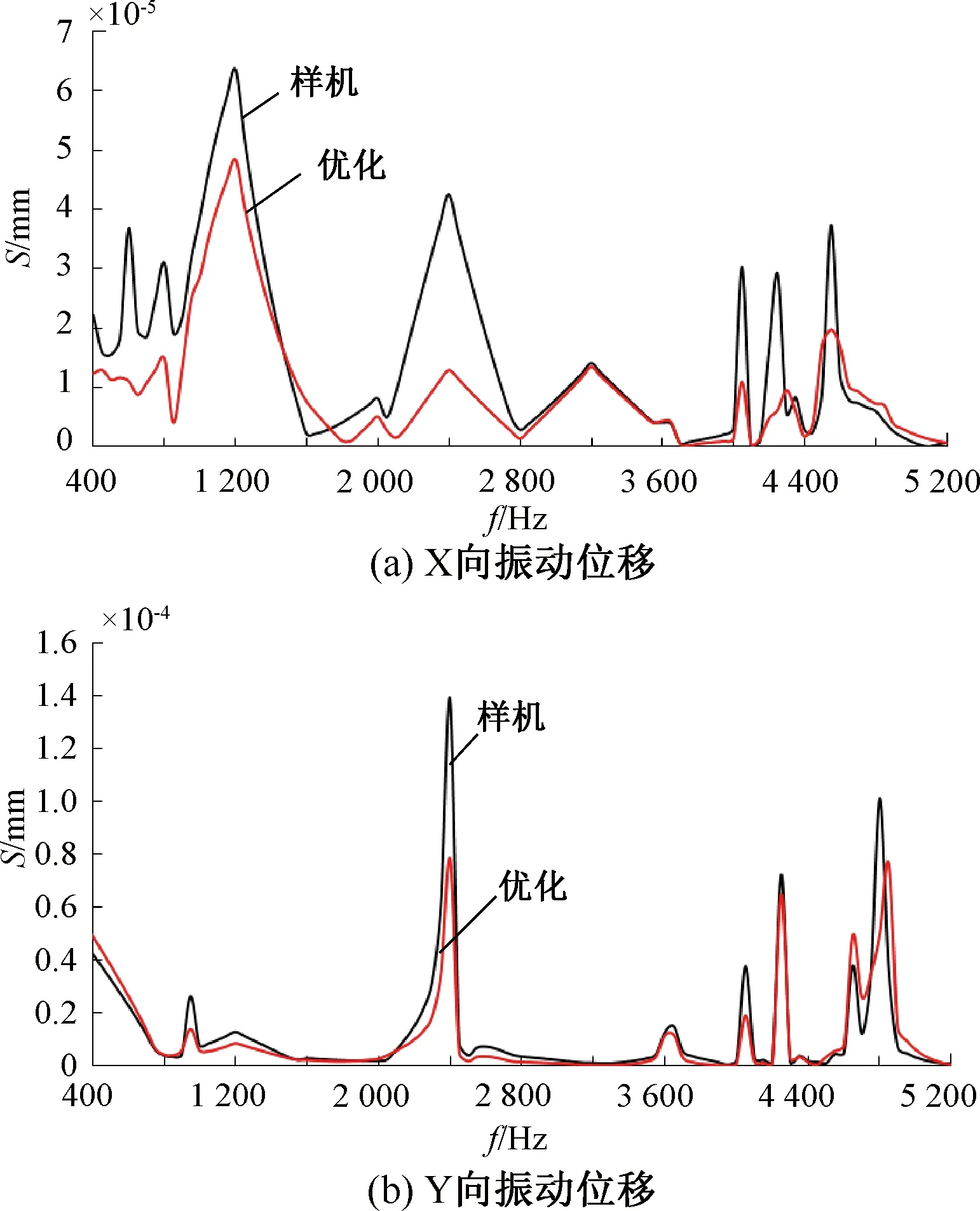
图13 驱动电机定子外表面振动位移幅值对比图

由图13分析可以得到，电机振动位移幅值有明显的降低：在2 400Hz频率位移分量处，X向振动位移下降了69.95%，振动幅值从4.26×10-5mm降低到了1.28×10-5mm；Y向振动位移幅值下降了43.6%，振动幅值从1.383×10-4mm降到了0.78×10-4mm；在1 200 Hz频率位移分量处，振动位移的降低在X向最为显著，下降了25%，从6.4×10-5mm降到了4.83×10-5mm。其他频率位移分量处也有明显的降低，说明通过最优化方法得到的电机结构参数最优解可以较为明显地提升驱动电机的振动性能。

表2是样机与优化电机的结果对比。对表2进行分析后可以发现，本文优化后的电机与初始样机相比，在驱动性能基本保持不变的基础上，转矩脉动和振动位移方面都有了明显的优化，说明本文采用粒子群算法和BP神经网络相结合的方法获得的是约束条件下电机结构参数组的最优解。

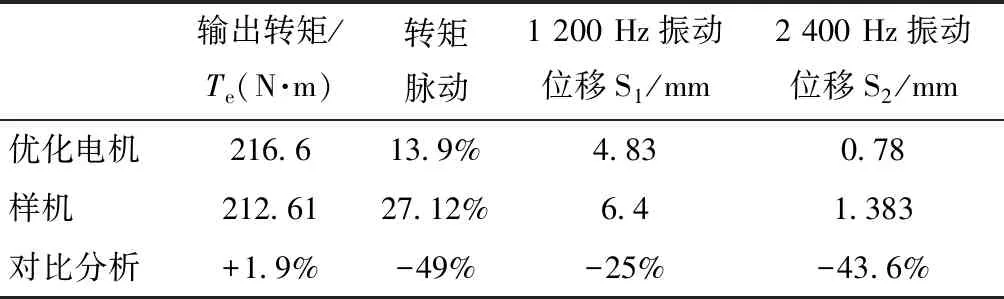
表2 样机与优化电机结果对比

4 结 语

本文探究了电机驱动及振动性能受电机主要结构参数变化的影响趋势。研究发现，隔磁桥间距、定子槽口宽度、气隙长度和永磁体厚度等4个结构参数对电机性能都有较大的影响，且气隙长度和隔磁桥间距的变化会导致电机振动性能和驱动性能呈现矛盾变化的趋势。

基于BP神经网络方法选择输入变量为电机主要结构参数，输出变量为电机的转矩脉动、径向电磁力幅值的主要频率分量和输出转矩，建立并拟合映射模型，使用相对误差法对BP神经网络模型进行测试，得到平均相对误差最大不超过5%，证明了神经网络模型预测的准确性。

使用粒子群算法的全局优化能力对电机进行优化并计算电机结构参数的最优解：定子槽口宽度Bso=1.8 mm、隔磁桥间距wrib=10.1 mm、永磁体厚度H=8.7 mm、气隙长度l=1.2 mm。将优化后的电机性能与样机进行对比，优化后的电机与初始样机相比，在驱动性能基本保持不变的基础上，转矩脉动和振动位移方面都有了明显的优化。