一种DPWM过调制技术的实现及应用
2023-03-03田星,李岚
田 星,李 岚
(太原理工大学,太原 030024)
0 引 言
脉宽调制(以下简称PWM)技术广泛应用于三相电压源逆变器,鉴于传统间矢量脉宽调制(以下简称SVPWM)在开关管损耗、谐波畸变率、直流侧电压利用率等方面不能达到综合最优,国内外学者提出了各种基于SVPWM算法:文献[1]分析推导了不连续脉宽调制(以下简称DPWM),并总结出采用DPWM策略时需要在开关损耗与谐波畸变之间权衡;文献[2-3]分别研究了单一考虑开关损耗或谐波畸变情况下,采用DPWM1相电压调制波谐波畸变率小,采用DPWM3时逆变器开关损耗最小;文献[4]提出了扩大线性调制区的五段式PWM 能有效利用直流侧电压来提高逆变器输出基波电压;文献[5]分析了SPWM优化过调制具有谐波少的优点;文献[6]总结出过调区调制度与谐波畸变率的密切联系。
针对上述算法均未考虑开关管损耗、谐波畸变率、直流侧电压利用率三者统一效果的不足,本文提出了一种改进的DPWM过调制技术,通过在异步电机调速系统的仿真证明,调速系统性能在多方面得以提升进而达到了综合最优的效果。
1 SVPWM过调制原理
SVPWM基本电压矢量及扇区分布如图1所示。

图1 空间电压矢量及扇区分布图
根据伏秒平衡原理:
UTS=UxT1+UyT2
(1)
式中:U为给定电压矢量(逆变器输出电压矢量);Ux、Uy为合成给定电压矢量的两个相邻基本电压矢量,并按照逆时针方向规定顺序为Ux在前,Uy在后;T1为Ux作用时间,T2为Uy作用时间;TS为开关周期。定义调制比m:
(2)
式中:Ud为直流侧电压值。
根据调制比m不同,分为3个区域:当m<0.906时为线性调制区;0.906≤m<0.952时为过调制I区;0.952≤m<1时为过调制Ⅱ区。
图2为过调制区合成电压矢量的轨迹图。

图2 过调制I区和过调制II区合成电压矢量轨迹
过调制I区αr和Ⅱ区αh简化公式[7]:
(3)
(4)
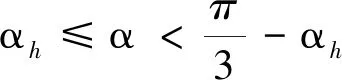
下面定义变量γ:
计算各个区域合成给定矢量的基本电压矢量及零矢量作用时间T1、T2、T0。
(1)SVPWM线性调制区(m<0.906)
(5)
T0=TS-T1-T2
(2)过调制I区(0.906≤m<0.952)
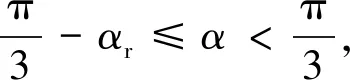
(6)
T0=TS-T1-T2
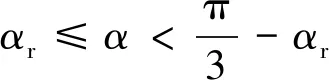
(7)
T0=0
(3)过调制Ⅱ区(0.952≤m<1)
①当0≤α<αh即γ<0时,
T1=TS,T2=0,T0=0
(8)

(9)
T0=0

T1=0,T2=TS,T0=0
(10)
通过对比不同区域时间计算公式不难发现,在式(5)~式(7)、式(9)中,T1与T2总是保持下列形式的关系:
(11)
文献[8]介绍了SVPWM线性调制区仿真模型及软件实现过程,下面承接SVPWM线性调制区的计算来推导过调制I区。
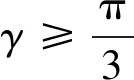
(12)
同理,根据过调制Ⅱ区计算公式,式(9)的实现也按照式(12)。
因此,只需要在根据m确定运行区域并判断γ大小,在不改变SVPWM线性调制区算法式(5)的基础上,加入式(8)、式(10)、式(12)限制,就可以完整实现全区域时间参数计算。
2 DPWM过调制
2.1 SVPWM算法原理
在线性调制区内,由给定电压矢量U在α-β坐标系下分量Uα、Uβ计算A、B、C和S,由S确定扇区号N,如表1所示。
(13)
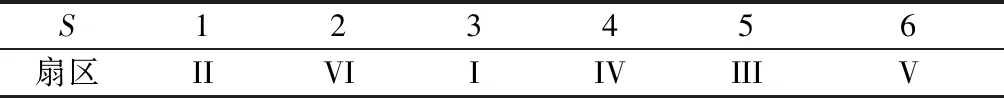
表1 S与扇区号对应关系
T1、T2可通过X、Y、Z的计算得出:
(14)
若在SVPWM线性调制区,则各扇区对应T1、T2可直接查表2得出;若在过调制区,再加入式(8)、式(10)、式(12)修正得出。
2.2 DPWM算法原理
不连续脉宽调制DPWM实现开关管在一个三角载波周期内仅使用零矢量V0或仅使用V7。如图3所示,DPWM1是在以基本矢量V1、V3、V5为中心的60°区间选用V7,剩余区间选用V0;DPWM2是在奇数扇区选用V7,剩余区间选用V0[9]。

表2 不同扇区基本电压矢量作用时间

图3 DPWM1和DPWM2扇区分布图
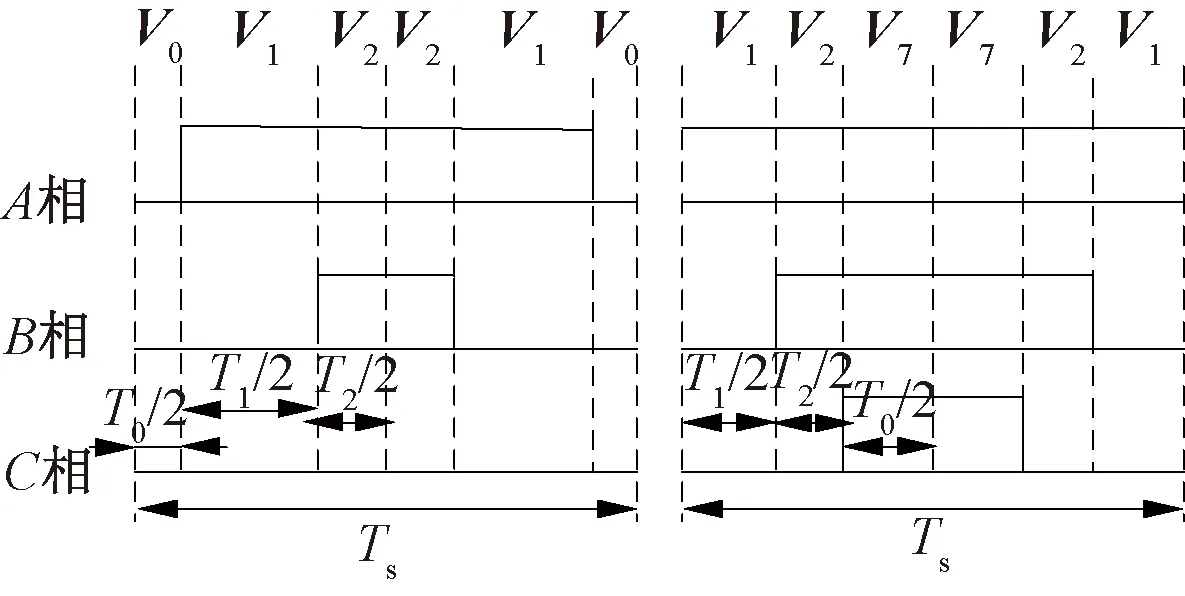
图4 仅使用V0或仅使用V7时开关序列图
仅使用V0和仅使用V7时开关序列如图4所示。一周期开关次数由SVPWM的6次减少到4次,损耗减少1/3。由图4得到矢量切换点:
(15)
(16)
综上所述,推导出DPWM1、DPWM2不同扇区对应的矢量切换点对应值Ton1、Ton2、Ton3,如表3、表4所示。

表3 DPWM1不同扇区对应的矢量切换值
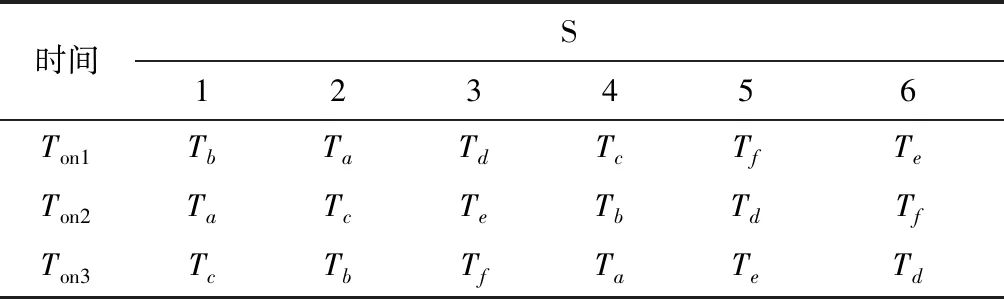
表4 DPWM2不同扇区对应的矢量切换值
2.3 DPWM过调制算法原理
结合DPWM和过调制原理,得到不同DPWM的调制算法,可以满足各个区域任意调制比输出有效的电压矢量,其流程图如图5所示,此时逆变器可以输出全区域平滑相电压调制波。

图5 DPWM全区域算法流程图

图6 3种算法下线性调制区相电压调制波
图6是在10 kHz开关频率下分别采用SVPWM、DPWM1、DPWM2方法,线性调制区的50 Hz相电压调制波,设置等腰三角载波幅值为0.000 05,可以看出,在一个周期内,DPWM相电压调制波总有被强制为幅值为0或0.000 05的顶点,此时一个桥臂上的开关不动作,减少了1/3开关损耗。
3 DPWM过调制仿真与实验结果
在MATLAB/Simulink软件平台上搭建异步电机矢量控制调速系统实验系统构建时采用与仿真相同的参数,异步电机(2.2 kW,380 V)的额定转速nN=1 420 r/min,极对数为2,定子额定电压频率fN=50 Hz,额定电流I1 N=5 A。直流侧电压Udc=514.59 V,定、转子参数统一折算到定子侧,电阻Rs=3.2 Ω,Rr=2.965 8 Ω,漏感Lls=0.014 3 H,Llr=0.014 3 H,互感Lm=0.265 4 H。将DPWM全区域算法应用到异步电机矢量控制系统,要求逆变器输出频率幅值均可变的电压,满足异步电机磁通恒定。随着转速升高,逆变器输出电压幅值增大,直流侧电压的设定已保证50 Hz时的电压幅值(即异步电机为额定转速)过渡到DPWM过调制区域。采用SVPWM、DPWM1和DPWM2全区域算法进行仿真,仿真在0.2 s突加额定负载。
对0.2 s加额定负载后实现FFT分析,图7为不同策略下a相相电压调制波形。

图7 定子相电压调制波形及谐波分析图
由图7看出,相比传统SVPWM线性调制,采用DPWM1过调制技术,电压波形谐波畸变率由原来的13.42%减小为8.00%,并且相电压基波调制波幅值由1.911×10-5提高到2.701×10-5。图8为不同策略下a相定子电流频谱图。在DPWM1过调制下,定子电流波形谐波畸变率由13.21%减小为4.43%。综上分析,采用全区域DPWM调制算法是正确可行的,并且在过调制区的作用效果尤为见效。

图8 定子相电流调制波形及谐波分析图
图9为异步电机额定转速和额定负载时,采用SVPWM、DPWM1和DPWM2过调制技术的实验结果。采用DPWM1过调制效果综合最佳,a相定子电流有效值约为6.36 A,大于SVPWM的5.21 A,直流侧电压约为513 V,小于SVPWM的570 V,直流侧电压利用率大幅提高;a相定子电压出现不连续的空白区,在此区域a相桥臂开关管不动作,此时a相定子电流较大,进而减小了开关损耗;DPWM1过调制a相定子电流波形平滑,毛刺比较小。综上分析与仿真基本吻合,说明DPWM过调制技术有效可行。
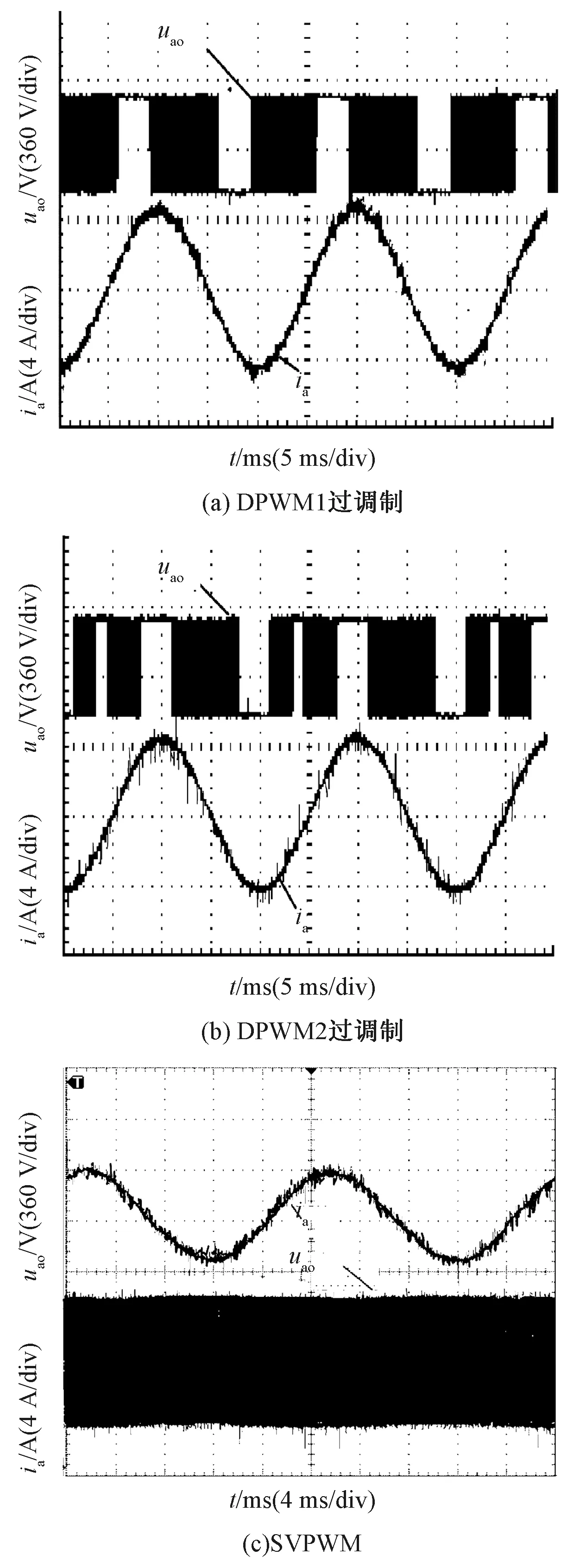
图9 a相定子电压电流实验波形图
4 结 语
本文提出了一种将DPWM和过调制结合的技术,并研究了其全区域实现的简单算法。本算法建立在传统SVPWM基础上,实现流程并未复杂化。通过异步电机矢量控制调速系统仿真和实验结果表明,本算法正确可行,并在过调制区内提高直流侧电压利用率、降低异步电机定子侧电压电流谐波畸变率、减少开关损耗方面有显著作用。
