改进GAN结合SDAE的传动系统主轴承故障诊断

陈 其

(商洛职业技术学院，商洛 726099)

0 引 言

近年来，可持续发展理念的深入和科学技术的进步，带动了太阳能、水电、风电等清洁能源的发展。据统计，截至2019年，我国累计风机装机容量达到2.1亿千瓦，风电已成为我国主要的发电方式之一。风电能源的蓬勃发展带动了风电站的建设，而风电机组是风电站的核心设备，因此，确保风电机组稳定安全运行，是保障整个风电站安全稳定运行的基础。由于风电机组运行工况复杂，其传动系统主轴承容易发生故障，要保证风电机组正常运行，有必要对其传动系统主轴承故障进行检测与诊断。

目前，针对主轴承故障诊断的诸多方法，主要是利用深度学习思想对其进行诊断。如卢锦玲等通过在辅助分类生成对抗网络上引入梯度惩罚，并在判别器网络中引入池化层，提出一种基于改进辅助分类生成对抗网络的风机主轴承故障诊断方法，可有效诊断风电机组主轴承故障，平均诊断准确率达到85%以上[1]。余萍等基于堆叠降噪自动编码器和人工变性天牛算法，提出一种ATLA-SDAE故障诊断方法，提高了故障诊断的效率[2]。卞东学等针对早期轴承故障信号弱的特点，结合经验模态分解和快速独立分量分析方法，提出一种基于CEEMDAN和FastICA的轴承故障诊断方法，突出了故障特征频率成分，提高了轴承故障诊断的准确率[3]。通过上述研究可以发现，现有风电机组传动系统主轴承振动故障诊断方法虽实现了风电机组振动故障诊断，但诊断的准确率约为85%，还有待进一步提高。

为解决该问题，本文研究结合辅助分类器生成对抗网络(以下简称ACGAN)与堆叠降噪自编码器(以下简称SDAE)，通过采用ACGAN生成高质量的新样本，以扩充传动系统主轴承故障样本量的大小，并利用SDAE从含噪样本中提取鲁棒性特征，提出一种基于ACGAN-SDAE故障诊断模型的传动系统主轴承故障诊断方法。

1 基本算法

1.1 ACGAN基本原理与网络结构

ACGAN是一种生成对抗网络(以下简称GAN)的变体算法，通过在GAN的生成器和判别器中添加类别标签，以辅助GAN处理附加信息时，利用类别标签信息生成高质量的生成样本，进而提高数据样本的差异性，使其尽可能被有效分类。

ACGAN的网络结构如图1所示[4]。其目标函数分为面向数据是否真实的代价函数Ls和面向数据分类准确性的代价函数Lc，表达式如下[5-6]：

Ls=Ex-Pdata[logP(source=real|xreal)]+

Ez-Pz[logP(source=fake|xfake)]

(1)

图1 ACGAN结构示意图

Lc=Ex-Pdata[logP(class=c|xreal)]+

Ez-Pz[logP(class=c|xfake)]

(2)

式中:Ex-Pdata表示对x的真实数据分布的期望值；Ez-Pz(z)表示从噪声采样z的期望值；xreal、xfake分别为x的真实和虚假分布。

ACGAN训练时，其目的是希望判别器尽可能区分真实数据和生成数据，并对数据进行分类，即使Ls+Lc最大。而生成器的目的是使生成数据尽可能判定为真实数据并被有效分类，即使Ls-Lc最小[7]。

1.2 SDEA网络结构

(3)

式中：θ(n+1)表示输出层参数集；g(·)为softmax分类器激活函数。

微调阶段通过Adam算法进行参数微调，通过最小化交叉熵损失函数LSDAE，实现整体微调[9]。LSDAE表达式：

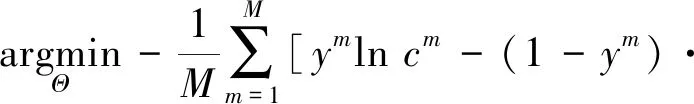
ln(1-cm)]

(4)

式中:Θ={θ1,θ2,…,θn+1}为SDAE参数集。

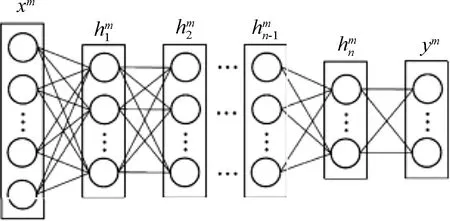
图2 SDAE网络结构

2 基于ACGAN-SDAE的传动系统主轴承故障诊断模型

2.1 模型整体框架

根据上述分析可知，ACGAN可良好地估计真实样本的实际分布，并扩充故障样本数量，有利于提高最终故障诊断的准确率。SDAE可实现良好的分类，并从含噪样本中提取鲁棒性特征。而实际传动系统主轴承故障数据相比于正常数据较少，容易导致模型故障诊断性能降低[10]；同时，实际诊断过程中存在大量的噪声数据干扰诊断结果，为解决上述问题，研究结合ACGAN和SDAE，提出一种基于ACGAN-SDAE的传动系统主轴承故障诊断模型整体框架，如图3所示。其中，生成器为一维卷积神经网络，通过使用类别标签辅助生成器获取原始传动系统主轴承故障样本的实际分布，以扩充故障样本数量[11]。判别器为SDAE，负责对输入样本真实性和故障类别进行判断。

图3 ACGAN-SDAE模型整体框架

2.2 判别器训练

判别器训练即是最小化真假标签的误差和故障类别标签的误差，如下式[12]：

(5)

(6)

(7)

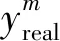
2.3 生成器训练

(8)

(9)

式中：LG为模型生成器的损失函数；ΘG为参数集；Lg为真假标签交叉熵损失误差[13]。

2.4 对抗训练

模型对抗训练分为以下三个步骤：首先生成器在含特定标签的潜在空间中生成随机噪声假样本；然后混合真实样本与假样本输入判别器中，对样本真实性和故障进行识别，并利用损失函数进行训练，更新判别器中的参数与标签；最后将判别器设置为不可训练，并固定其参数，更新生成器中的参数，以训练生成器生成更真实的假样本，实现训练判别器。重复上述操作，直至生成器和判别器均达到稳定状态，即完成了模型的对抗训练。

2.5 故障诊断流程

根据上述分析，将基于ACGAN-SDAE模型的传动系统主轴承故障诊断流程设计如下：

(1)数据获取及预处理。利用传感器收集传动系统的主轴承原始振动信号，由于其复杂性较高，需要采用快速傅里叶变换将原始振动信号转化为频谱信号。

(2)模型训练。将预处理后的数据按一定比例分为训练集和测试集，将训练集输入模型进行训练，直至模型稳定。

(3)故障分类。将测试集输入训练完成的ACGAN-SDAE模型中，输出诊断分类结果，即为故障诊断识别结果。

3 仿真实验

3.1 实验环境搭建

本实验在Ubuntu16.04操作系统上进行，通过Keras深度学习框架和Python3.6编程语言进行实现。系统配置Intel(R)Core(TM)i7-8700 CPU，NVIDIA GeForce GTX 1080 Ti GPU，内存为16 GB。

3.2 数据来源及预处理

本实验选用美国凯斯西储大学公开的CWRU滚动轴承数据集中，以12 kHz采样频率采集的1 750 r/min、1 772 r/min和1 797 r/min 3种转速下的电机振动数据，作为传动系统主轴承机械故障诊断的实验数据集。该数据集包括正常(Normal)和损伤直径为0.001 778 m、0.000 355 6 m、0.000 533 4 m的内圈故障(IF)、外圈故障(OF)、球故障(RF)共10种健康状况[14-15]。

为获取数据集中每段信号的频谱样本，实验前对数据集中的每段信号进行了快速傅里叶变换。为使诊断结果具有一定的参考性，实验对数据集进行了划分，将每个数据集划分为训练集和测试集两类，其中，每个训练集包括6 600个训练样本，每个测试集包括1 000个测试样本。具体划分情况如表1所示。表1中，A、B、C分别表示轴承负荷735 W、1 470 W、2 205 W。

表1 实验数据集划分情况

3.3 评价指标

本实验选用准确率(acc)作为评估模型性能的指标，其计算方法如下：

acc=(TP+TN)/(P+N)

(10)

式中：TP表示真正例；TN表示真负例；P表示所有正例；N表示所有负例。

3.4 参数设置

本实验将生成器学习率设置为0.002，通过Adam算法进行优化训练，第一个一维卷积层的内核大小设置为16，动量设置为0.8，激活函数设置为relu函数； 第二个一维卷积层的内核大小设置为8，激活函数设置为双曲正切tanh函数。将判别器的学习率设置为0.001，通过Adam算法进行优化训练。

考虑到噪声因子是影响ACGAN-SDAE模型诊断性能的关键因素，因此，通过实验方法选择适当大小的噪声因子。

为确定最佳噪声因子，实验通过设置不同噪声因子并分析不同噪声因子下模型的诊断准确率，选择最佳噪声因子。表2为不同大小的噪声因子进行10次实验后模型的诊断平均准确率。由表2可知，随着噪声因子的增大，模型的诊断准确率先升高后下降，当噪声因子为0.3时，模型的故障诊断准确率达到最大值，为98.67%。因此，本实验将ACGAN-SDAE模型的噪声因子设置为0.3。

表2 不同噪声因子下模型的诊断准确率

3.5 结果与分析

3.5.1 不同故障样本量下模型的诊断效果

为检验ACGAN-SDAE模型在不同故障样本量下的诊断效果，实验通过将数据集A中每种状态模式下的不平衡率设置为25%、40%、50%、75%、100%，研究了不同故障样本量模型的诊断效果，并将模型与SDAE、SVM、MLP常用故障诊断模型进行比较。为避免随机误差对结果的影响，实验分别采用不同模型进行了10次实验，并以10次实验结果的平均值作为最终结果。不同模型的诊断结果如表3所示。

表3 不同故障样本比例下模型的故障诊断准确率

由表3可知，样本故障量增加可提高模型故障诊断准确率。整体来看，相较于SDAE、SVM、MLP模型，ACGAN-SDAE模型在不同故障样本量下的故障诊断准确率均具有一定的优势，尤其是在25%的小故障样本量下，ACGAN-SDAE模型的故障诊断优势更明显，故障诊断准确率可达到78.66%，说明ACGAN-SDAE模型在小故障样本量下仍具备良好的故障诊断能力。分析其原因是，ACGAN-SDAE模型生成新的带标签样本，提高了小故障样本的质量，进而提高了模型的故障诊断性能。因此，ACGAN-SDAE模型对不同故障样本量的传动系统故障诊断具有良好的诊断性能，且在小故障样本量下的故障诊断性能更优于对比模型。

3.5.2 不同信噪比下模型的诊断结果

为验证ACGAN-SDAE模型对不同故障信噪比下的故障诊断性能，实验在A数据集中通过添加不同信噪比的高斯噪声检测模型的抗噪性能，并将其与SDAE、SVM、MLP常用故障诊断模型进行比较，结果如表4所示。由表4可知，不同信噪比下，ACGAN-SDAE模型故障诊断准确率最高，可达到90%以上，即使是在信噪比为-6 dB条件下，ACGAN-SDAE模型的故障诊断准确率也能达到90%以上，相较于其他对比模型提高了8%左右，说明ACGAN-SDAE模型对不同信噪比的传动系统故障诊断具有良好的诊断性能。分析其原因是，ACGAN-SDAE模型结合了对抗学习和降噪原理，具备了良好的抗噪性能。

表4 不同信噪比下不同模型的故障诊断准确率

3.5.3 跨不同负载域数据下模型的诊断结果

为验证ACGAN-SDAE模型在跨不同负载域数据集下对故障诊断的自适应性能，实验分别以735 W、1 470 W、2 205 W负载下的任意一种样本进行训练，另外两种样本作为测试，具体数据如表1所示，并将其与SDAE、SVM、MLP常用故障诊断模型进行比较，结果如图4所示。由图4可知，在跨不同负载域下，ACGAN-SDAE模型平均故障诊断准确率达到93%以上，说明在跨不同负载域下，ACGAN-SDAE模型对传动系统故障的诊断效果具有一定的优越性。

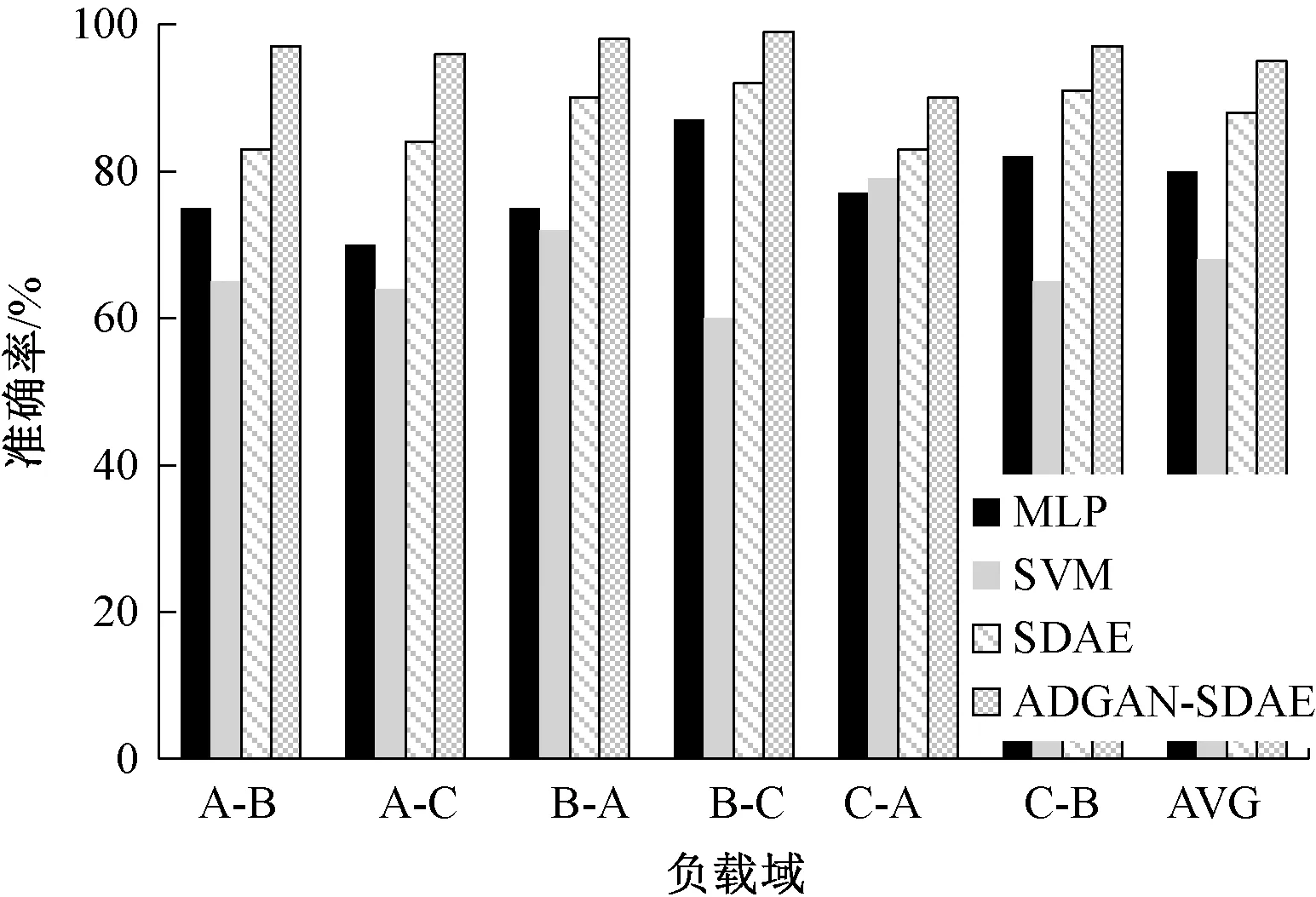
图4 跨不同负载域下不同模型的诊断准确率

整体来看，所有模型从数据集C到A和A到C的故障诊断准确率均低于其他跨域的故障诊断准确率，说明当两个工作条件差异明显时，无论是ACGAN-SDAE故障诊断模型还是其他故障诊断模型，其适应性均有所下降。但综合来看，ACGAN-SDAE模型在传动系统故障诊断上具有明显的优势。

3.5.4 模型特征提取与样本生成结果可视化

为更好地反映ACGAN-SDAE模型在故障诊断过程中的性能，实验利用t-SNE技术，将模型的特征提取结果和样本生成结果进行了可视化，结果如图5所示。由图5可知，ACGAN-SDAE模型可以将相同传动系统故障类型的特征进行聚合，将不同传动系统故障类型的特征进行分离，区分不同传动系统故障类型，具有良好的特征提取能力。

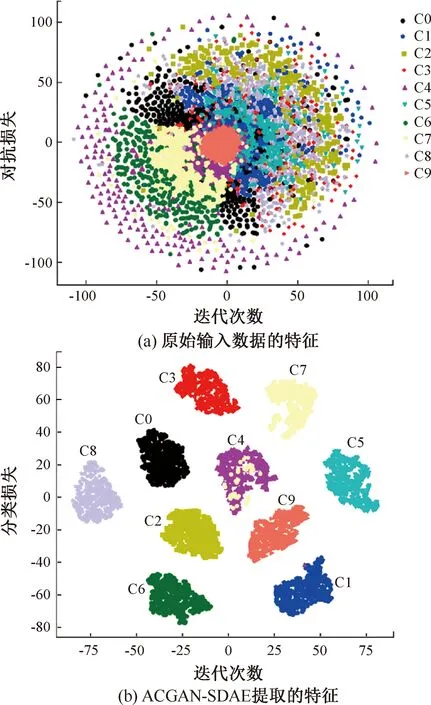
图5 ACGAN-SDAE模型特征提取可视化结果

图6为ACGAN-SDAE模型训练损失可视化结果。由图6可知，随着训练进行，模型的对抗损失和分类损失逐渐趋于稳定，说明ACGAN-SDAE模型通过训练可获取理想故障诊断模型。

图6 ACGAN-SDAE模型训练损失

图7为不同故障状态下原始样本与生成样本的频谱示例。由图7可知，不同故障状态下原始样本分布与其生成样本分布相似程度较高，说明ACGAN-SDAE模型生成了高质量样本，提高了模型故障诊断的泛化性能。

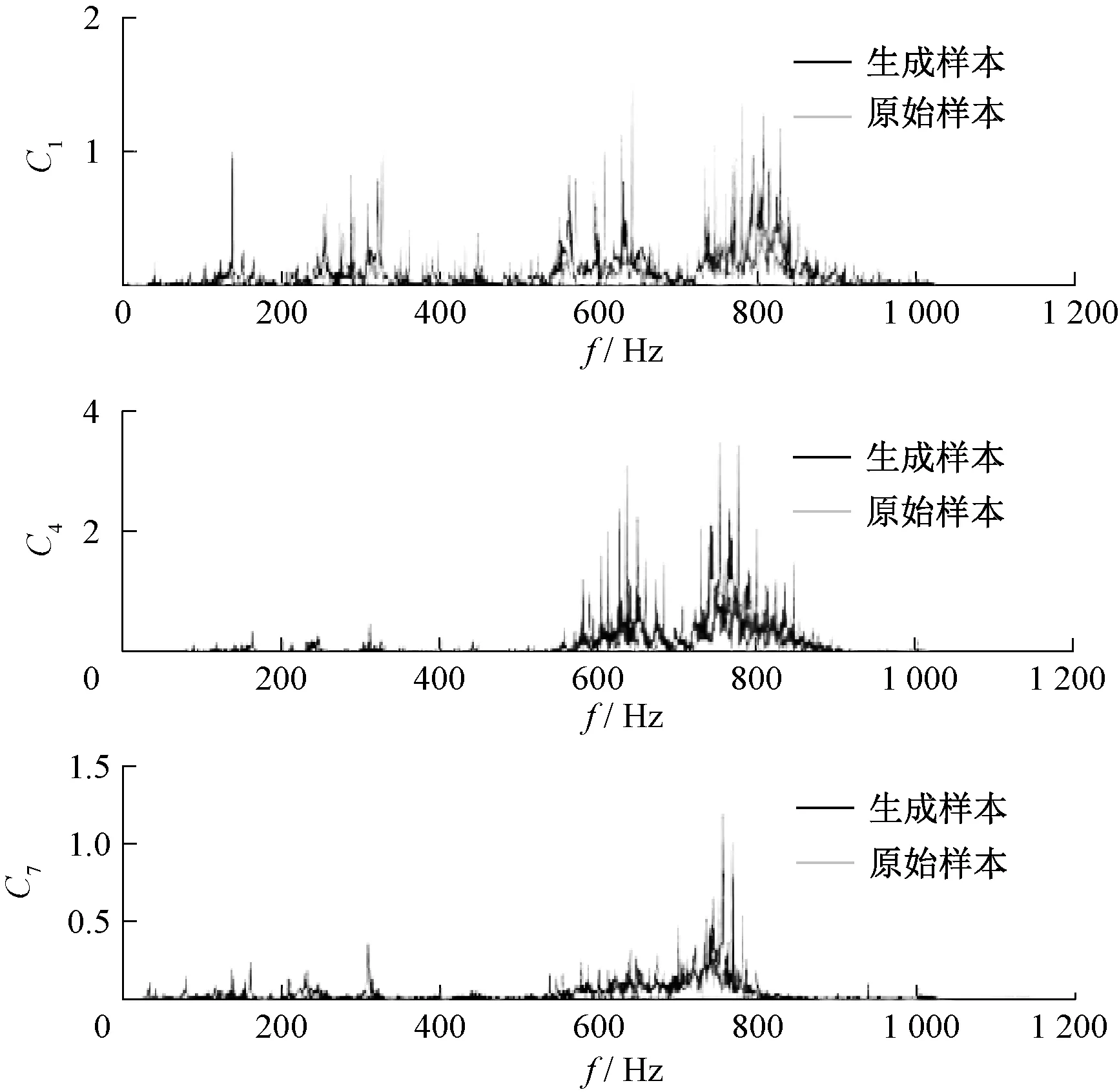
图7 原始样本和生成样本的频谱

4 结 语

综上所述，基于ACGAN-SDAE的传动系统主轴承故障诊断模型，通过采用ACGAN生成高质量的新样本，扩充了传动系统主轴承故障样本量的大小，并利用SDAE从含噪样本中提取鲁棒性特征，提高了故障诊断的准确率，可有效诊断不同故障样本量下的传动系统主轴承故障，且具有良好的域自适应性和抗噪性能，平均故障诊断准确率达到90%以上，相较于SDAE、SVM、MLP常用故障诊断模型，ACGAN-SDAE模型具有一定的优越性，为传动系统主轴承故障诊断提供了理论基础。但受条件限制，本研究仍存在一些不足有待改进，主要表现在研究采用的是单一振动信号作为故障诊断模型的输入信息，而实际传动系统主轴承故障的振动信号复杂，单一振动信号不能完全包括多种状态信息，降低了模型的鲁棒性。为提高模型的鲁棒性，下一步研究将尝试采用多尺度信号作为模型输入。