永磁同步电机拓扑结构对散热性能的影响

刘慧娟，周佳明，易元元，宋腾飞

(北京交通大学 电气工程学院，北京 100044)

0 引 言

随着物流行业的迅猛发展，叉车作为灵活高效的搬运工具在实际应用中发挥了巨大作用。在低碳、环保的大背景下，各类电动车应用广泛。电动叉车具有污染小、噪声低等优势，同时其操作控制简便灵活，大大降低了驾驶员的工作强度，提高了工作效率[1]。电动叉车用驱动电机先后经历了直流电机、异步电机、永磁同步电机等。永磁同步电机具有优越的起动性能和调速性能，过载能力强[1-2]，较好地迎合了电动叉车的工作需求，且其体积小、质量轻、结构简单、效率高[2]，因此得到广泛的研究以及开发利用。

国内外学者对永磁同步电机的拓扑结构进行了大量优化，这些优化主要通过探究电机定转子尺寸对转矩、损耗、效率等电磁性能的影响规律，得到较优的拓扑结构，从而提升电机的电磁性能。如北京航空航天大学郭宏[3]等人基于永磁同步电机的磁场解析模型，推导了效率、电时间常数和结构参数之间的关系，从而达到了优化电机效率及动态性能的目的。太原理工大学高泽梅[4]等人采用田口实验法，通过改变永磁体及定子相关尺寸，实现了对一台内嵌式永磁同步电机的空载损耗、运行效率等电磁性能的优化。比利时学者Thibaut Labbé[5]等人通过对永磁同步电机转子半径等拓扑结构的优化，实现了转矩质量比的最大化。伊朗学者SeyedArmin Mirnikjoo[6]等人基于田口法，通过改变永磁体宽度、定子槽宽度等参数，对表贴式永磁同步电机的齿槽转矩和空载反电动势进行了多目标优化。

以上优化均未考虑电机拓扑结构的改变对永磁同步电机散热性能的影响。事实上，定转子部分尺寸的变化会对电机的热源以及散热性能产生直接影响，散热性能在很大程度上又影响了电机的功率密度。因此，在优化过程中如果不考虑散热性能，那么电机的性能将很难达到最优。

本文建立了改进的等效热网络模型，计算了水冷型内置式永磁同步电机的温度场，并通过有限元温度场模型验证了其准确性。然后采用所建立的热网络模型，计算了电机在不同定子齿宽、定子槽宽、定子槽深、永磁体夹角等参数下的温度分布，探究了拓扑结构对永磁同步电机散热性能的影响，为电机优化过程中同时考虑电磁场与温度场提供一定的参考。

1 热网络模型的构建

在电机设计及优化阶段，需频繁改变电机的拓扑结构并计算相关性能，采用有限元法计算温度场，会耗费大量的时间成本以及计算资源。本文将构建简化的等效热网络模型，在保证计算精度的前提下大大降低计算成本。

1.1 电机的热源

永磁同步电机的损耗主要有绕组铜耗、铁心损耗、机械损耗以及附加损耗[7]。基于电机结构的复杂、运行情况变化多样等原因，电机损耗很难准确计算，目前多采用经验公式逼近，后期通过实验引入修正系数对损耗数据进行修正处理[8]。

电机的绕组铜耗又称为交流铜耗，可表示[9]：

pAC=pDC+pSK+pPR

(1)

式中：pDC为绕组电流产生的欧姆损耗，称为直流铜耗；pSK为由趋肤效应引起的附加铜耗；pPR为由临近效应引起的附加铜耗。

其中直流铜耗可表示：

pDC=mI2R

(2)

式中：m为电机相数；I为相电流有效值；R为每相绕组的阻值。

根据Bertotti分离模型[10]，铁耗可表示：

(3)

式中：ph为磁滞损耗；pe为涡流损耗；pa为附加损耗；Bm为磁密幅值；f为交变磁场的变化频率；kh、ke、kα分别为磁滞损耗系数、涡流损耗系数、附加损耗系数，其值大小由材料属性决定，可通过实验测得。

永磁同步电机的机械损耗主要分为风摩损耗和摩擦损耗。一般采用简单的公式或者根据已经生产的实验数据来确定，可参考如下表达式近似计算[10]。

摩擦损耗：

(4)

式中：pf为摩擦损耗；F为轴承负荷；d为滚珠中心直径；v为滚珠中心的圆周速度。

风摩损耗：

pw=1.75qvv2

(5)

式中：qv为通过电机的空气体积流量；v为转子圆周速度。

1.2 空心圆柱体的热网络模型

电机的大部分零件可以等效地看成一个空心圆柱体，如定子、转子以及外壳。如图1所示，其内外径分别为r1、r2，轴向长度为L。

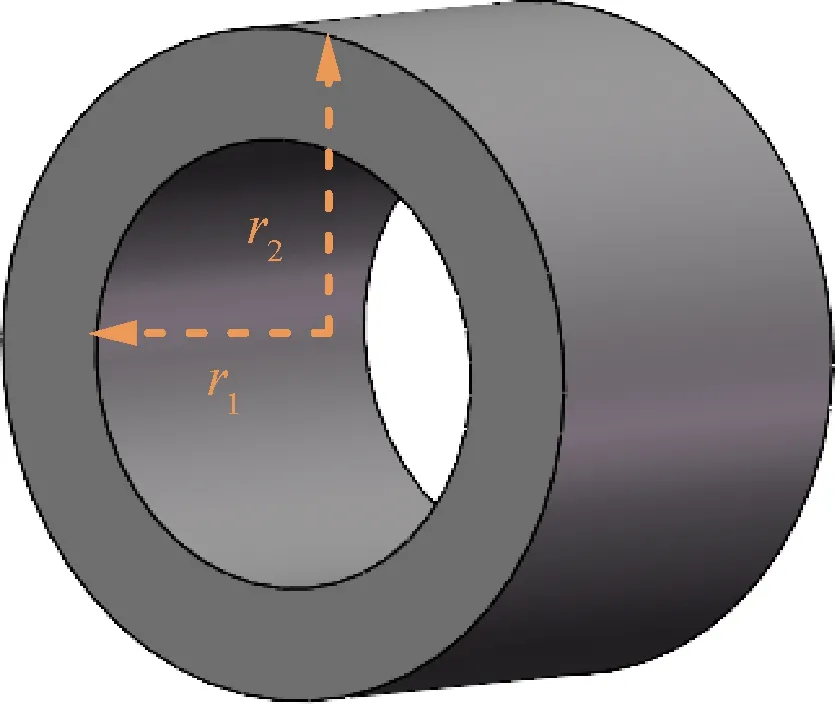
图1 空心圆柱体

假设其内部存在损耗，则圆柱体的温度升高，它通过热传导及表面与空气的对流将热量散发出去。该空心圆柱体的热阻可表示[11]：

(6)

式中：λ为导热系数。

该模型过于简单，无法准确计算温度。因此，Mellor[11]提出了更准确的热网络模型，然而Mellor热网络计算的结果是平均温升，与最大温升有偏差。LI Kai等人分别采用Mellor热网络与有限元方法计算了同一空心圆柱体的稳态温升，两者的最大温升相对误差达到10%。基于此，LI Kai等人提出了计算最大温升的热网络[12]。

本文参照以上模型[11-12]，建立了空心圆柱体的热网络结构，如图2所示。

图2 空心圆柱热网络模型

其径向传导热阻：

(7)

(8)

轴向传导热阻：

(9)

轴向对流热阻：

(10)

式中：Rr1、Rr2、Ra和Rair分别为空心圆柱体的内部径向、外部径向、轴向传导热阻以及轴向对流热阻；hair是空气的自然对流系数。

根据热传导方程，利用关键点的温度可计算出空心圆柱体的径向温度分布以及最大温升。空心圆柱体内径向热传导的稳态方程[12]：

(11)

式 (11)为二阶常系数非齐次线性微分方程，求其一般解可得空心圆柱体的径向温度分布表达式：

(12)

对式 (12)求导可得极值，即径向最高温度：

(13)

极值半径：

(14)

此外，通过解析计算可得空心圆柱体轴向最高温度表达式[12]：

(15)

式中:Ta(L)与Ta(0)分别表示空心圆柱体轴向上底面及下底面的温度值。

等效热网络模型建立之后，还需对其进行校准，以满足精度要求。本文主要采用实验和有限元法对包括接触电阻以及对流散热系数等进行修正。

采用三维有限元法计算空心圆柱体的稳态温度场时，可归结为以下边值问题。

在直角坐标系下，导热微分方程可表示：

(16)

其边界条件：

(17)

式中:λx、λy、λz分别为沿x、y、z方向的导热系数；q为热流密度；T1为边界面S1上的给定温度；n为边界面(S1、S2)上的法向量；α为S2表面的对流散热系数；T0为S2周围介质的温度。

如图3及图4所示，分别采用有限元法及热网络法计算了空心圆柱体的温度场分布。可以看到，本文建立的等效热网络具有较高的准确性。

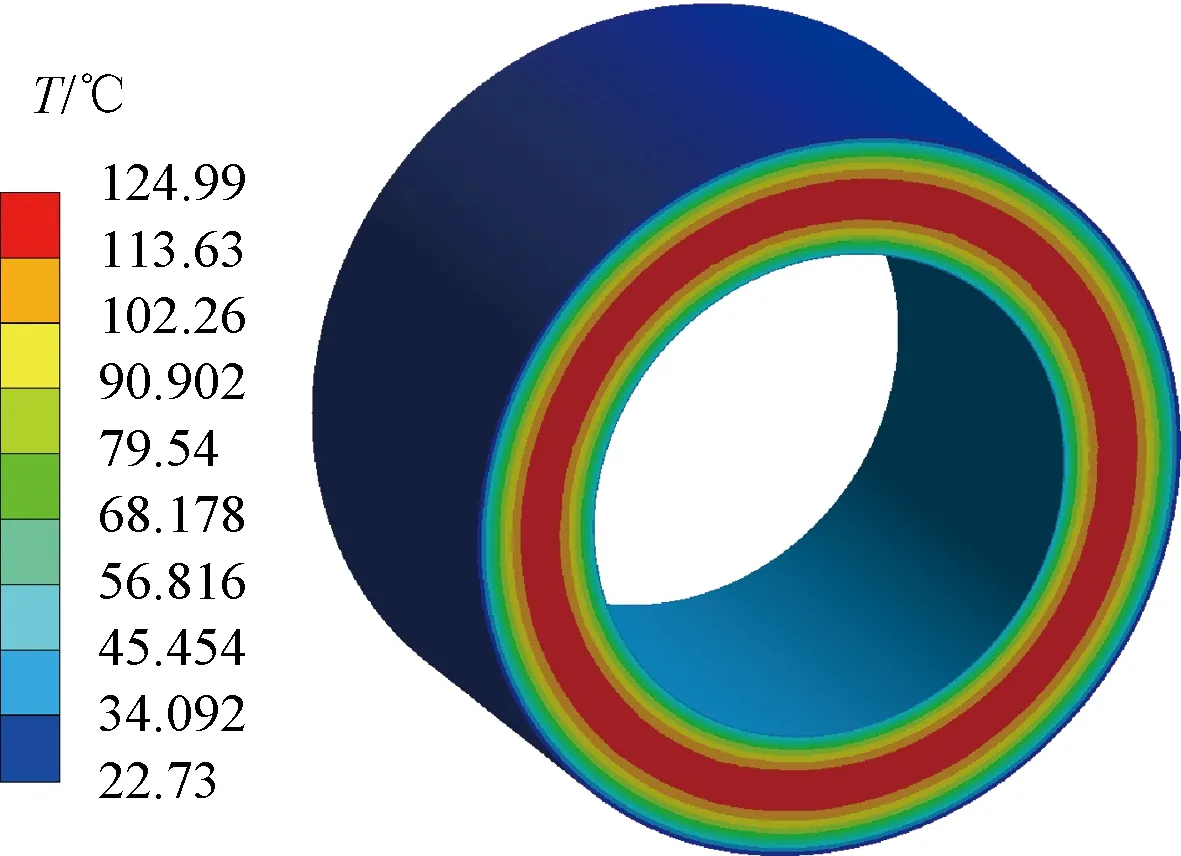
图3 空心圆柱体的温度分布(有限元法)

图4 有限元及热网络法温度对比

1.3 永磁同步电机的热网络模型

本文的研究对象为水冷型内置式永磁同步电机，其结构示意图如图5所示，主要由机壳、定子铁心、绕组、转子铁心、永磁体、转轴等组成，采用定子水冷的冷却方式，Z字形水道嵌在机壳中。

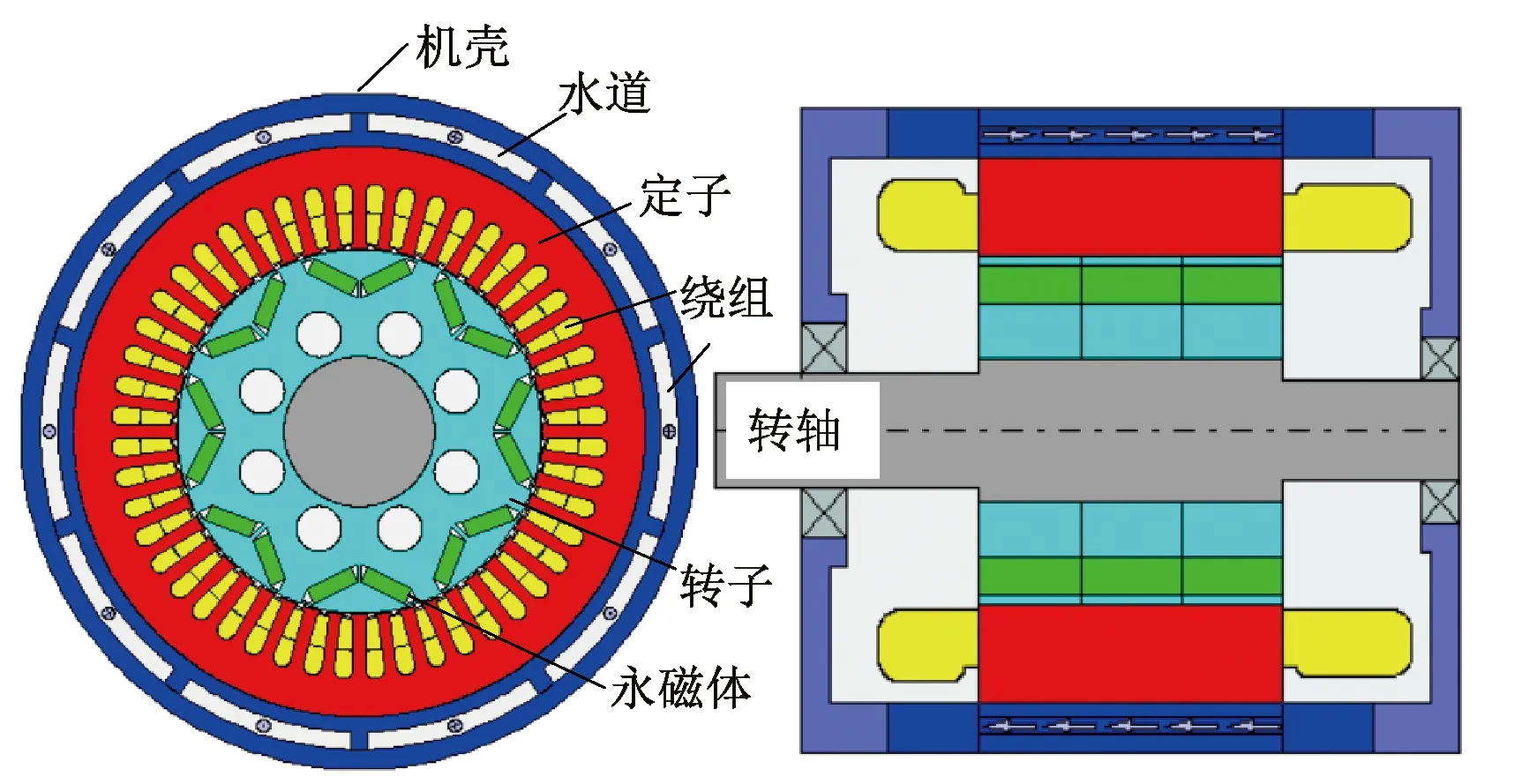
图5 水冷型内置式永磁同步电机结构图

根据本文所建立的空心圆柱体等效热网络模型，创建了内置式永磁同步电机的等效热网络模型，如图6所示。其中热源pfe_sy、pfe_st、pfri、pwind、pfe_rt、pmagnet、pfe_ry、pcu1、pcu2分别表示定子轭铁耗、定子齿铁耗、轴承摩擦损耗、转子表面风摩耗、转子齿铁耗、永磁体损耗、转子轭铁耗、有效绕组铜耗、绕组端部铜耗。

图6 永磁同步电机的等效热网络模型

各部分的传导热阻由式 (7)～式(10)得出。除传导热阻外，两个相互接触的物体之间的间隙同样可以看成是这两个物体之间的一个热阻，称这种特殊的传导热阻为接触热阻[12]。如壳体与定子之间的间隙、永磁体与转子的间隙等。接触热阻Ra可以表示：

(18)

式中:h为等效接触厚度；λc为等效导热系数；A为接触面积。接触厚度取决于材料性能、加工工艺、加工温度等条件，接触热阻计算比较复杂，一般通过实验获得[13]。根据接触面粗糙度，接触厚度h一般可分为三个等级：接触良好(0.01 mm)、接触一般(0.03 mm)和接触不良(0.08 mm)。本文取h=0.03 mm。

水冷永磁同步电机的散热主要靠机壳外表面和水套的自然对流，对流热阻可表示[12]：

(19)

式中：hcnv为对流散热系数，Acnv为对流散热面积。水套和外壳的对流散热系数分别为1 500～2 500 W/(m2·℃)和10～30 W/(m2·℃)，此系数可以从Fluent中获得。

2 永磁同步电机温度场计算及验证

根据所建立的等效热网络模型，本文针对8极48槽内置式永磁同步电机进行温度场计算，并采用有限元法对其进行验证。电机的主要参数如表1所示。

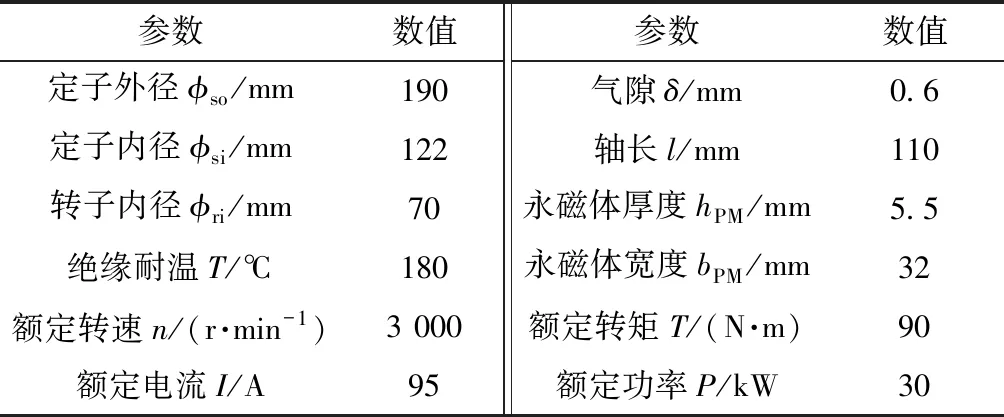
表1 永磁同步电机的主要参数

损耗是电机的热源，精确计算电机损耗也很重要，各部分损耗的计算方法前文已详细给出。本文永磁同步电机中使用的导线直径为0.7 mm，在最大工作频率(600 Hz)下算得趋肤深度约为2.7 mm，远大于导线直径。此外，通过有限元法算得的附加铜耗小于直流铜耗的2%，因此，本文的附加铜耗忽略不计。

需要注意的是，定子和转子不同区域的铁耗密度分布是不同的。额定条件下不同时刻的铁损分布如图7所示。可以看出，定子和转子的铁损分布不均匀，转子铁损主要集中在外圆区域，定子铁损主要集中在定子铁心的齿上，原因是定子齿部的磁密较为饱和[14]。因此，定子和转子的齿和轭需要分别计算，以确保结果的准确性。此外，由于损耗值是随温度变化而变化的，在计算损耗时需要多次迭代，直到收敛误差小于初始值的1%为止。

图7 不同时刻永磁同步电机的铁耗分布云图

本文采用有限元法计算了电机额定工况下各部分的损耗，得到的结果如表2所示。通过所建立的热网络模型，计算了电机在额定工况下工作120 min的温度分布，环境温度及冷却液温度设置为65 ℃，水流量为10 L/min，得到电机的瞬态温升曲线如图8所示。可以看到，电机长时间运行在额定工况并达到稳态时，绕组端部由于散热差，其发热较为严重，温升也最高。机壳由于离水道距离最近，因此其散热能力最好，温升也最低。随着与水道距离的逐渐

表2 额定工况下各部分损耗

增大，电机稳定状态的温升值也在增高。虽然永磁体的损耗很小，但是永磁体散热主要依靠与机壳内部的空气对流散热，散热能力较差，因此其温升比较高。由图8可以看到，绕组端部的最高温度为140.2 ℃，温升为75.2 ℃，小于温升限值100 ℃。有效绕组最高温度为131.3 ℃，小于绝缘耐温180 ℃。转子齿、永磁体、转子轭的温升曲线基本重合。

图8 额定工况瞬态温升曲线(热网络法)

为验证本文等效热网络的准确性，采用有限元法(3D-fluent)计算了永磁同步电机额定工况下的温度分布。设置环境温度为65 ℃，电机运行趋于稳定后，各部分温度分布如图9所示。对比热网络和有限元方法得到的稳态最高温度，结果如表3所示。可以看到，除机壳和水套外，其余各个重要部分的最高温度误差保持在10%以内，验证了热网络模型的准确性。

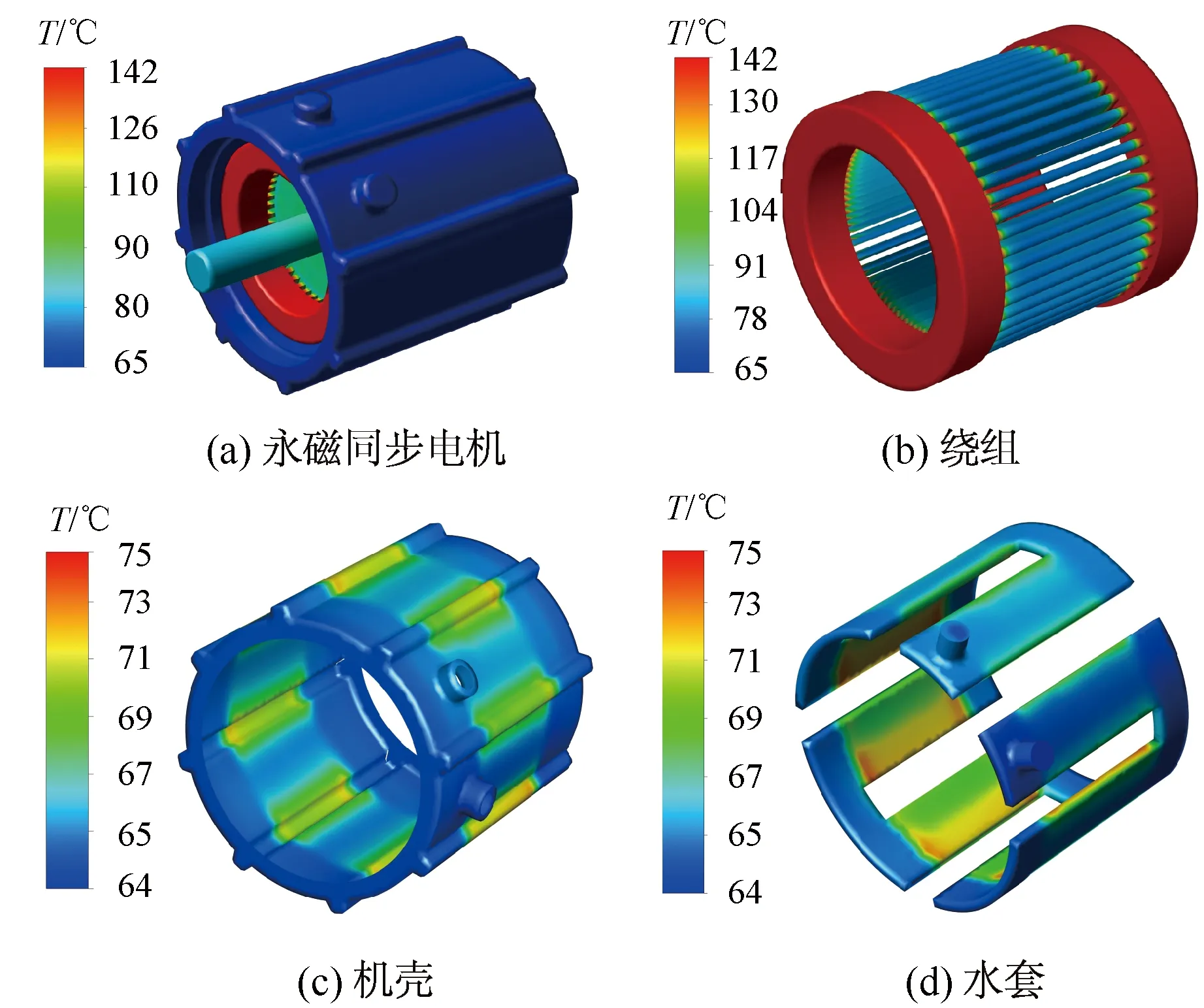
图9 额定工况下各部分稳态温度分布(有限元法)

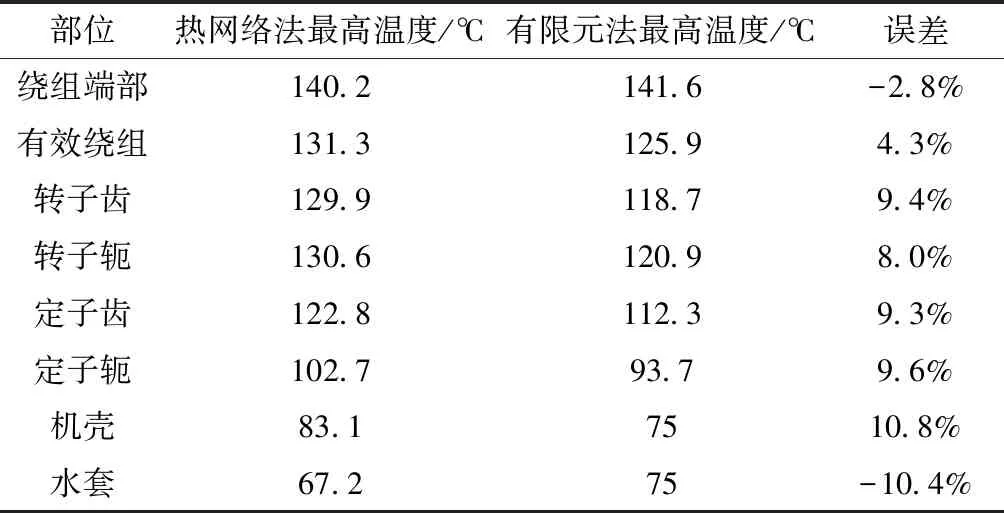
表3 额定工况下各部分最高温度及误差

3 拓扑结构对散热性能的影响

3.1 定转子拓扑结构对损耗的影响

在电机设计过程中，往往需要通过不断改变电机的拓扑结构，使得电机的性能达到更优，在这个过程中，主要关注的是电机的电磁性能。实际上，拓扑结构的改变会对散热性能产生直接影响，散热性能又会反过来影响电磁性能。如果忽略散热性能的影响，电机性能将很难达到真正的最优。本文将对永磁同步电机部分尺寸的变化对电机热源以及散热性能的影响进行探究。

图10为永磁同步电机拓扑结构示意图。定义定子齿宽为Bs1，定子槽宽为Bs2，定子槽深为Hs1，定子轭宽为Hs2，永磁体夹角为θ。

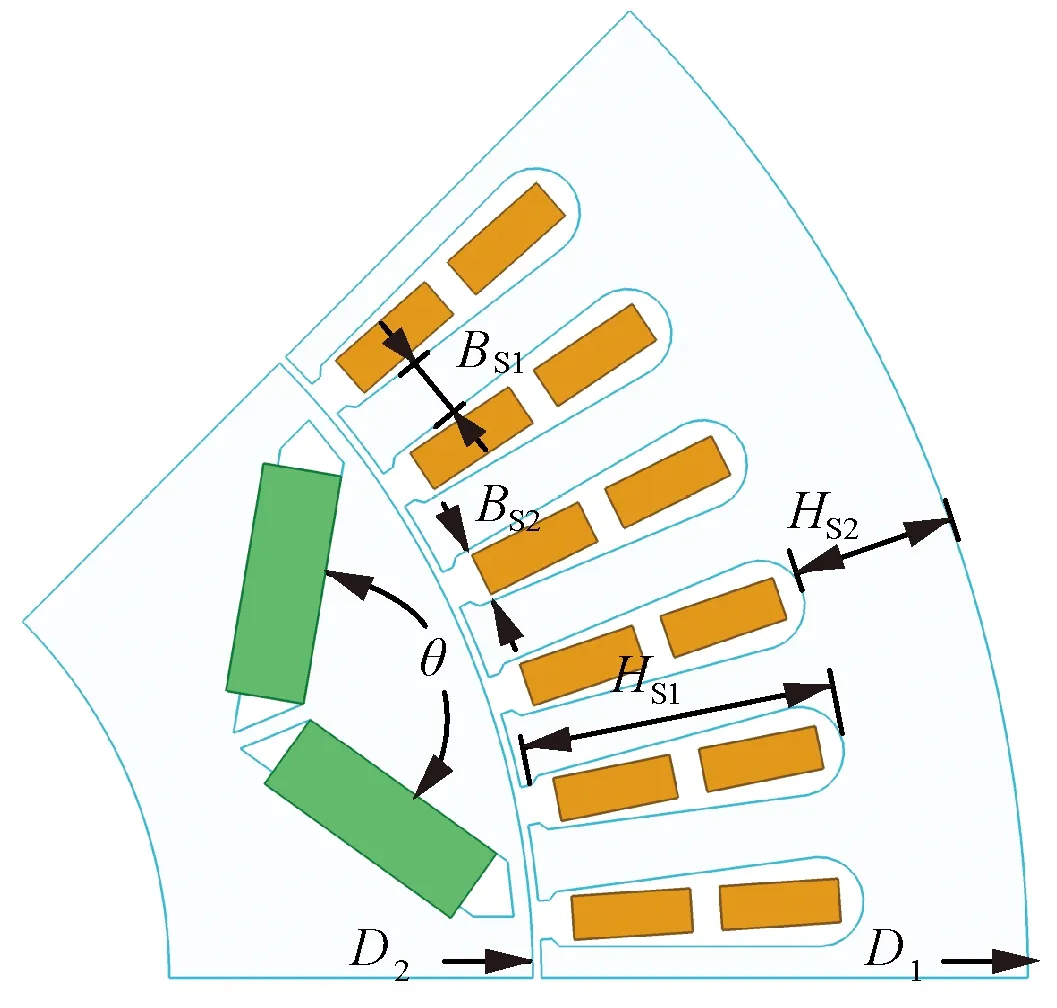
图10 内置式永磁同步电机拓扑参数

为减少变量，本文定义齿槽比：

(20)

定义齿轭比：

(21)

损耗作为电机的热源，其变化会对电机温升产生很大的影响。图11～图13分别探究了额定工况下齿槽比、齿轭比以及永磁体夹角的变化对电机各部分损耗产生的影响。随着齿槽比的增大，槽面积减小，定子中的磁密发生变化，从而影响了定子的铁耗。从图11中可以看出，齿槽比越大，铁耗越大，而绕组铜耗基本保持不变。虽然齿槽比的增大会使永磁体损耗减小，但永磁体损耗占总损耗的比例非常小，因此电机的总损耗在增大。

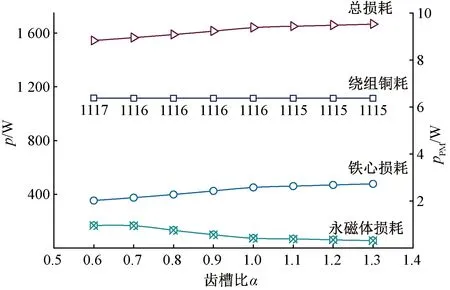
图11 齿槽比对各部分损耗的影响

图12 齿轭比对各部分损耗的影响

图13 永磁体夹角对各部分损耗的影响

同样，随着齿轭比的增大，定子轭部厚度减小，磁密受到影响，从而使得定子铁耗增加。从图12中可以看出，由于槽面积的变化引起绕组电阻变化，绕组铜耗也在随着齿轭比的增大而增大，永磁体损耗先呈增大的趋势，然后又开始减小。

从图13可以看到，永磁体夹角变化的过程中对永磁体损耗影响较大，其余损耗基本保持不变。由于永磁体损耗占总损耗比例非常小，可以忽略不计。

3.2 定转子拓扑结构对散热性能的影响

除损耗外，定转子拓扑的尺寸对电机散热性能也会产生直接的影响。例如，定子槽的周长会影响绕组与铁心之间的热阻，从而影响电机的温升，齿槽比与齿轭比的改变均会影响定子槽周长。为探究拓扑结构对散热性能的直接影响，假定电机的损耗保持不变，则α与β对电机各部分最高温度的影响如图14所示。

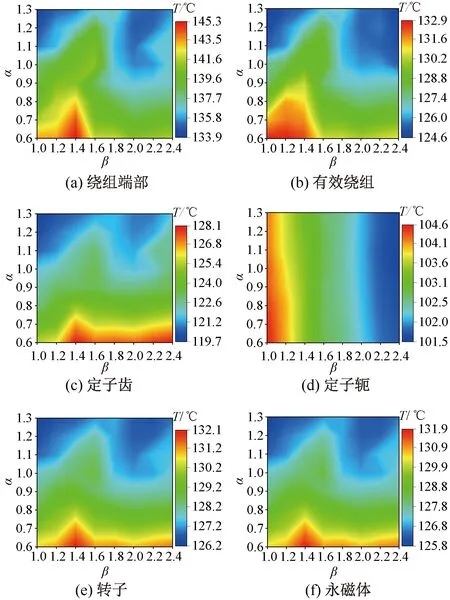
图14 假定损耗不变时齿槽比与齿轭比对各部分温度的影响

可以看出，α与β在变化过程中，最高温度发生了显著变化。其中绕组端部、有效绕组、定子齿、转子、永磁体的最高温度变化趋势基本保持一致，随着α的增大，各部分最高温度呈一个增大的趋势；而在β增大的过程中，各部分最高温度先呈增大的趋势，然后又逐渐减小。

而定子轭最高温度的变化趋势与其余部分不同。从图14(d)可以看出，齿槽比α对定子轭的最高温度基本无影响，而齿轭比β在增大过程中，定子轭的最高温度逐渐降低。这是因为齿轭比增大，则定子轭的厚度减小，由于定子轭的大部分热量都通过冷却水带走，定子轭的最大温度出现在离水道最远的点，其厚度减小，则这个点离水道的距离就减小，因此其散热能力增加，最高温度也就降低了。

此外，拓扑参数的变化会影响电机的损耗。在电机实际运行中，损耗的变化与散热能力的变化同时影响着电机的温升。考虑损耗的变化时，α以及β对电机各部分最高温度的影响如图15所示。可以看到，受到损耗影响，电机各部分最高温度的变化趋势与恒定损耗时有明显不同。随着α的增大，绕组端部最高温度有降低的趋势； 随着β的增大，其最高温度先增大再减小，最后又增大。

图15 损耗变化时齿槽比与齿轭比对各部分温度的影响

对于有效绕组来说，α较小时，其最高温度变化规律与绕组端部相同；而α较大时，其最高温度随着β的增大而增大，且β>1.6时，其最高温度有了明显的升高。定子齿则随着α的变化，其最高温度变化趋势不明显，随着β的增大，其最高温度也增大。受损耗影响，定子轭的温度变化趋势与恒定损耗时完全相反。转子与永磁体的变化趋势则比较一致，这是由于转子与永磁体离水道的距离较远，其散热主要依靠与机壳内部空气的对流散热，因此受与水道的距离影响较小，其二者散热能力也相近。

总的来说，在高齿槽比、低齿轭比的拓扑结构下，电机的绕组端部、有效绕组以及定子齿部的散热性能较好。而在低齿槽比、低齿轭比的拓扑结构下，电机的定子轭、转子以及永磁体的散热性能较好。

同样，分别假定损耗不变以及考虑损耗变化时，永磁体夹角的变化对电机散热性能的影响做了探究，如图16、图17所示。 可以看到， 在假定损耗不变时，永磁体夹角对电机的散热性能不会产生影响。而在考虑损耗变化时，永磁体夹角对电机的散热性能影响非常小，几乎可以忽略不记。因此，在电机优化过程中，可忽略永磁体夹角对散热性能的影响。

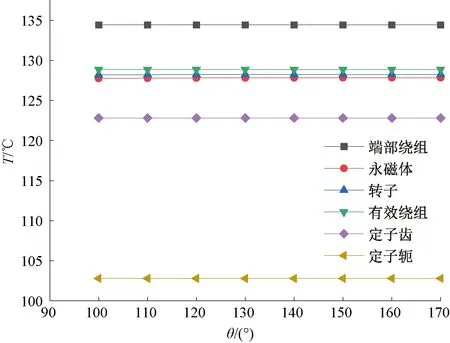
图16 假定损耗不变时永磁体夹角对各部分温度的影响

图17 损耗变化时永磁体夹角对各部分温度的影响

4 结 语

本文以30 kW电动叉车用水冷型内置式永磁同步电机为研究对象，通过建立的热网络模型，探究了不同定子结构对电机的热源以及散热性能的影响，得到结论如下：

1)齿槽比与齿轭比的增大均会引起电机总损耗的增大，这主要是由于齿槽比与齿轭比的增大导致定子铁心磁密变大，从而使得铁心损耗增大。其余各部分损耗变化不明显，因此铁耗的变化趋势主导了总损耗的变化趋势。

2)假设在电机运行过程中损耗不发生改变，齿槽比与齿轭比的变化会对电机的温升特性产生直接的影响。在齿槽比增大过程中，散热能力逐渐增强。当α>1.1且β>2.0时，电机各部分的散热能力均达到最佳。此时绕组端部最高温度为133.9 ℃，相较于α=0.6，β=1.4时绕组端部的最高温度下降了11.4 ℃。

3)在电机实际运行中，损耗会发生变化，在α>1.1且β<1.2时，电机的绕组端部、有效绕组以及定子齿的散热能力达到最佳，绕组端部的最高温度为140.6 ℃，相较于最高时下降12.9 ℃；而在α<0.8且β<1.2时，定子轭、转子以及永磁体的散热性能达到最佳，此时定子轭最高温度为104.8 ℃，相较于最高时下降4.1 ℃。转子最高温度为132.2 ℃，相较于最高时下降5.9 ℃。

4)永磁体夹角的变化对电机各部分损耗以及电机散热性能的影响均较小。在电机优化过程中，可忽略永磁体夹角对散热性能的影响。