两种不同折射率圆柱镶嵌获得的光子晶体的带隙

陈义万，陈昭蓉，李文兵，杜海霞，张群芝

（1.湖北工业大学理学院，湖北 武汉 430068；2.湖北省鄂北水资源管理局，湖北 武汉 430000；3.火箭军工程大学，陕西 西安 710025；4.武汉市板桥中学，湖北 武汉 430072）

0 引言

光子晶体是介质结构在空间周期性的排列构成的。电磁波在光子晶体中传播也有传播禁带，就是在某些特定波长范围的电磁波不能在光子晶体中传播。光子晶体概念从1987年被提出以来[1-2]，由于它的潜在的优越性能，成为研究热点。光子晶体在光子晶体光栅、光子微腔、光波导、雷达全反射涂层都有潜在的良好的应用。通过设计各种对称性不同的结构，获得尽可能宽的带隙，是光子晶体结构研究中的一个重要内容[3-15]。分析研究光子晶体带隙，有平面波展开法，转移矩阵法，有限时域差分法（FDTD）等等。本文用有限时域差分法（FDTD），分析几种镶嵌式光子晶体结构的带隙。

1 二维正方格子和两种结构镶嵌光子晶体的带隙

我们选用ZnO 圆柱，它的折射率n=2.81，背景是空气，折射率n=1。介质柱的半径r=0.2μm，介质柱组成10×10 阵列，圆柱之间的距离（晶格常数）a=6r=1.2μm。入射使用平面电磁波，在前期预计算基础上，入射波的波长范围设定为λ=1.0-2.0μm，计算中使用FDTD 专用软件计算，边界条件使用完全匹配层（PML）。信号检测使用100 个频率抽样点。ZnO 圆柱二维光子晶体的结构如图1 所示。

图1 ZnO 圆柱二维光子晶体结构

光波通过ZnO 圆柱二维光子晶体结构后的能量和波长的关系图，如图2 所示。从图2 中可以看出，在1.25-1.35μm，1.50-1.58μm 有明显的两个能量禁带。

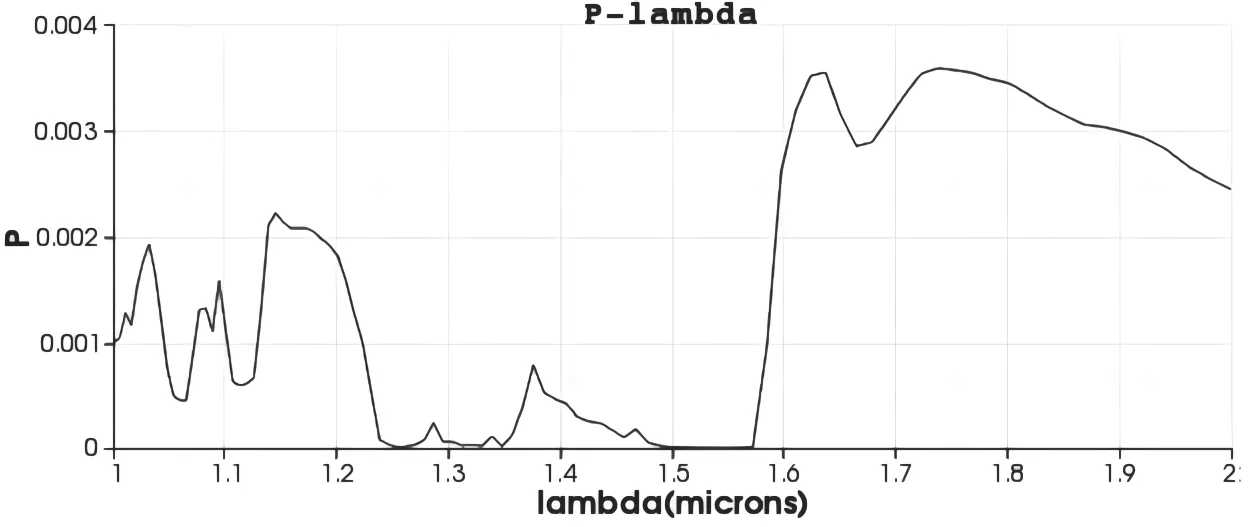
图2 ZnO 圆柱二维光子晶体的透射能量与波长的关系（P-lambda 图）

我们选用Si 圆柱，折射率n=3.45，背景是空气，折射率n=1。介质柱的半径r=0.2μm，介质柱组成10×10 阵列，圆柱之间的距离（晶格常数）a=6r=1.2μm。入射使用平面电磁波，入射波的波长范围设定为λ=1.0 -2.0μm，计算中使用FDTD 专用软件计算，边界条件使用完全匹配层（PML）。信号检测使用100 个频率抽样点。Si 圆柱二维光子晶体的结构类似于图1。光波通过Si 圆柱二维光子晶体结构后的能量和波长的关系图，如图3 所示。

图3 光波通过Si 圆柱二维光子晶体结构后的能量和波长的关系图（p-lambda 图）

从图中可以看出，在1.25-1.35μm，1.70-1.82μm，有两个明显的带隙。在图1 和图3 的基础上，我们把ZnO 圆柱镶嵌到Si 圆柱的晶体中，可以看成ZnO 圆柱光子晶体相对于相同结构的Si 圆柱光子晶体在平面内发生了平移，

如图4 所示。让平面光波在这样的复合结构光子晶体结构中的传播，看它的带隙与两个子结构的带隙有何区别。

图4 由ZnO 圆柱镶嵌在Si 圆柱光子晶体中的结构

计算中入射使用平面光波，入射波的波长范围设定为λ=1.0 -2.0μm，边界条件使用完全匹配层（PML）。信号检测中采样200 个频率抽样点。光波通过图4 镶嵌二维光子晶体结构后的能量和波长的P-lambda 关系图，如图5 所示。

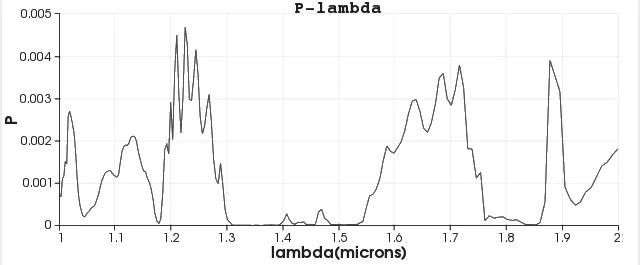
图5 光波通过由ZnO 圆柱镶嵌在Si 圆柱光子晶体中的结构的P-lambda 图

从图中可以看到，带隙在1.30-1.53μm，1.75-1.85μm。对比图2，图3，图5，ZnO 圆柱光子晶体和Si 圆柱光子晶体的带隙，在由它们镶嵌构成的光子晶体中，这些带隙都出现并且向长波长方向发生了偏移。

下面考察一种二维正方格子光子晶体的带隙。该光子晶体的介质柱材料为Si，折射率n=3.45，介质柱半径r=0.2μm，晶格常数入射光波为平面波，波长范围λ=1.0-2.0μm，平面波入射方向沿着正方格子的对角线方向，光波检测采样200 个频率抽样点。结构如图6 所示，光波通过光子晶体后透射的能量波长如图7 所示。

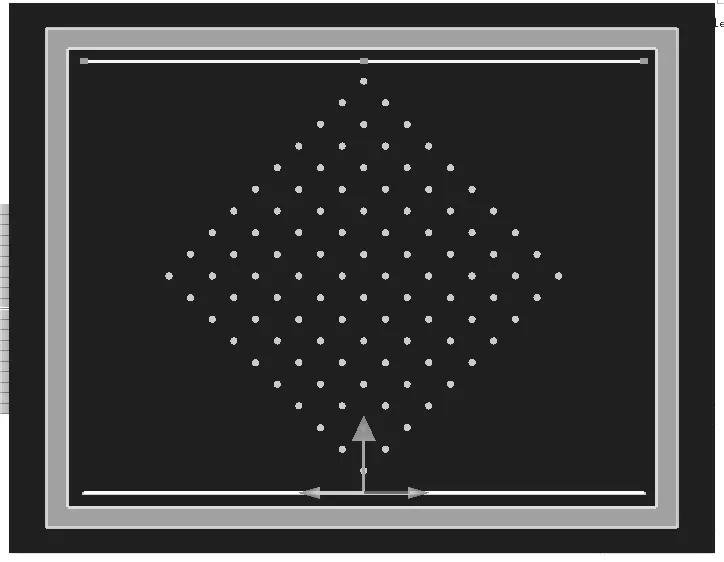
图6 介质柱半径r=0.2μm，晶格常数=1.6 96μm 的Si 光子晶体

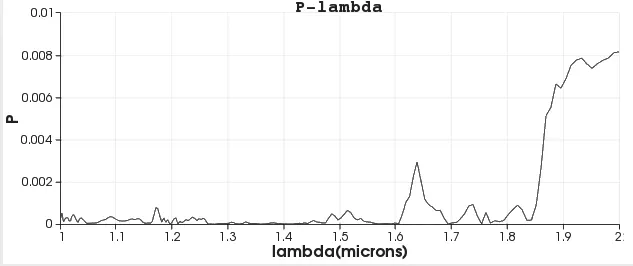
图7 介质柱半径r=0.2μm，晶格常数=1.6 96μm 的Si 光子晶体的光透射P-lambda 图

从图7 可以看到，在平面光沿光子晶体对角线入射时，带隙波长范围是λ=1.26-1.46μm，1.55-1.60μm。下面把图6 的Si 圆柱光子晶体镶嵌到图1 的ZnO 二维光子晶体中，结构图如图8 所示。

图8 把图6 的Si 圆柱二维光子晶体镶嵌到图1 的ZnO 二维光子晶体中形成的新的光子晶体

在图8 中，入射光波为平面波，波长为λ=1.0-2.0μm，光波通过光子晶体后，在监测点对传播的光波数值进行200 个频率点抽样。二维边界使用完全匹配层（PML）。得到的透射光的能量与波长的关系图如图9 所示。

图9 把图6 的Si 圆柱二维光子晶体镶嵌到图1 的ZnO 二维光子晶体中形成的新的光子晶体的光波透射图（P-lambda 图）

从图9 中可以看到，光子晶体的带隙范围为λ=1.25-1.45μm。由于图8 的结构是把图6 的结构镶嵌到图1中形成的，把图9 与图2 和图7 对比，在短波长部分的λ=1.25-1.35μm 的带隙在镶嵌光子晶体中出现，长波长部分的带隙λ=1.70-1.75μm 没有出现。也就是说，镶嵌光子晶体的带隙并不能完全出现子晶体的带隙。

2 两种不同材料的圆柱按行间隔排列，构成的二维正方光子晶体和六角光子晶体的带隙

下面考虑一种新的光子晶体结构，它们由ZnO(n=2.81)和Si(n=3.45)圆柱间隔排列而成，介质圆柱半径r=0.2μm，圆柱之间的距离即晶格常数a=6r，20×20 阵列，结构图如图10 所示。

图10 由ZnO 和Si 圆柱介质按行间隔排列形成的二维正方结构光子晶体

实验中边界使用完全匹配层（PML），用平面电磁波入射，波长范围为λ=0.4-2.0μm，为了使分析的数据更准确，在检测数据时，对频率抽样500 个频率点。电磁波通过该光子晶体后的P-lambda 图如图11 所示。

图11 光通过由ZnO 和Si 圆柱介质间隔排列形成的二维正方结构光子晶体后的P-lambda 图

从图11 可以看出，该结构的光子晶体的带隙在λ=1.25-1.38μm，1.6-1.9μm，由于图10 的结构是Zn 圆柱和Si 圆柱间隔排列而成，把图11 和图1 以及图3 对比，发现图1 和图3 中的带隙在图11 中都出现，且向长波长方向有小幅移动。

下面考虑由ZnO 圆柱（n=2.81）构成的六角形二维光子晶体。介质柱半径r=0.2μm，圆柱之间距离a=4r=0.8μm，组成15×15 的六角形结构。结构如图12 所示。入射波为平面电磁波，波长范围λ=0.4-2.0μm，对透射电磁波进行500 个频率抽样点采样。边界使用完全匹配层。得到如图13 的透射波能量与波长关系图。

图12 由ZnO 圆柱构成的六角形二维光子晶体

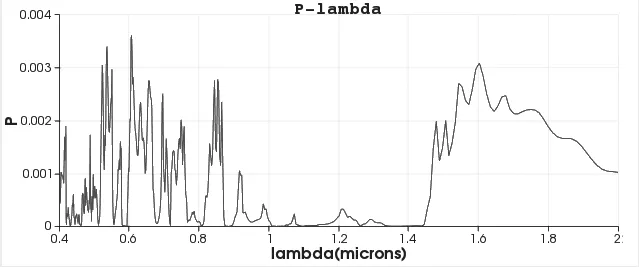
图13 由ZnO 圆柱构成的六角形二维光子晶体的透射波P-lambda 图

下面考虑由Si 圆柱（n=3.45）构成的六角形二维光子晶体。介质柱半径r=0.2μm，圆柱之间距离a=4r=0.8μm，组成15×15 的六角形结构。结构与图12 相同。

入射波为平面电磁波，波长范围λ=0.4-2.0μm，对透射电磁波进行500 个频率抽样点采样。边界使用完全匹配层。得到如图14 的透射波能量与波长关系图。

图14 由Si 圆柱构成的六角形二维光子晶体的透射波P-lambda 图

从图14 中可以看出，该结构的带隙范围是，λ=1.38-1.55μm，1.72-1.78μm。

下面考虑一种光子晶体，它由ZnO 和Si 圆柱按行间隔排列而成。介质圆柱的半径r=0.2μm，圆柱之间的距离a=4r=0.8μm，结构如图15 所示。计算中入射波为平面电磁波，波长范围λ=0.4-2.0μm，对透射电磁波进行500 个频率抽样点采样。边界使用完全匹配层。得到如图16 的透射波能量与波长关系图。

图15 由ZnO 和Si 圆柱按行间隔排列而成二维六角形光子晶体，浅色是ZnO 圆柱，深色是Si 圆柱，15×22 阵列

图16 由ZnO 和Si 圆柱按行间隔排列而成二维六角形光子晶体的电磁波透射能量－波长图

从图16 可以看出，带隙的范围是λ=1.25-1.45μm。把图16 和图13，图14 对比，图16 的带隙与图13，图14 的带隙之间，并没有完全的对应关系。说明在二维六角形光子晶体中，由两种单纯成份的圆柱介质的按行间隔排列，并不能把每一种单纯成份的光子晶体的带隙实现。前述各个光子晶体结构的带隙总结见表1。

表1 二维正方格子光子晶体与镶嵌式光子晶体以及按行间隔排列的光子晶体的带隙

3 结语

本文研究了由ZnO 圆柱（折射率n=2.81）和Si 圆柱（折射率n=3.45）分别构成的二维正方格子光子晶体，通过计算，得到了光波通过光子晶体后的带隙。然后，把ZnO 圆柱晶体镶嵌到Si 圆柱二维光子晶体中，计算了镶嵌得到的光子晶体的带隙，发现原来的ZnO 光子晶体和Si 圆柱光子晶体的带隙，在镶嵌后的光子晶体中都能够出现，但是带隙位置向长波方向移动。另外研究了由ZnO 圆柱和Si 圆柱按行间隔排列构成的二维正方格子光子晶体，发现ZnO 圆柱光子晶体和Si 圆柱光子晶体的带隙，在间隔排列的光子晶体中都能够实现，但是带隙的位置向长波长方向移动。按照类似的方法，把ZnO 圆柱介质和Si 圆柱介质按行间隔排列，构成二维六角形光子晶体，原来的单纯由ZnO 圆柱构成的二维六角形光子晶体的带隙和单纯由Si 圆柱构成的二维六角形光子晶体的带隙，在按行间隔排列的二维光子晶体中，并不能完全实现。这样的结果，可能与二维六角形格子的对称性比正方格子的对称性低。这种镶嵌式光子晶体和按行间隔排列光子晶体的带隙性质，为寻找宽带隙的光子晶体提供了一个新途径。