普通光源的时空相干度分析
2011-03-20张国华
张国华
(山东省海洋环境监测技术重点实验室 山东省科学院海洋仪器仪表研究所 山东青岛 266001)
1 引言
在自然界中,两束光相遇经常发生,但干涉现象并不多见,原因在于干涉现象必须满足一定的条件才会出现.下面是必要条件:
(1)两列光波的频率相同;
(2)两列光波的光矢量的振动方向相同或存在相平行的振动分量;
(3)两列光波在相遇点位相差恒定或光源的初位相恒定.
补充条件:
(1)相干光的振幅不能相差太大;
(2)相干光的光程差不能太大,最大不能超过波列长度.
以上条件在常规条件下难以满足,原因在于实际光源的复杂性.其中光源的非单色性和宽度是影响光波相干性的两个重要因素[1].
时间相干性和空间相干性正是从光源的非单色性和宽度两个角度来描述对光波相干性的影响.在教学和实验中,一般是分别讲述时间相干性和空间相干性,对统一的理解时空相干性造成困难.本文在光源的非单色性和宽度对干涉条纹可见度影响公式的基础上推导出普通光源的时空相干度的计算公式.
2 光源的非单色性对干涉条纹可见度的影响——时间相干性
严格的单色光是不存在的,实际光波只能看成线宽为Δλ的许多不同频率成分的理想单色波的叠
加[2].
图1为杨氏双孔实验.设波列长度ΔL=Nλ,其中λ为波列的中心波长.根据光强的极值条件,当两相干波列在P点的光程差δ=kλ时,P点的光强有最大值Imax.假设一个空间周期的单个扰动在P点产生的光强为I0.而此时两波列中的相干部分为相长干涉,故重叠部分单个扰动在P点产生的光强为4I0.
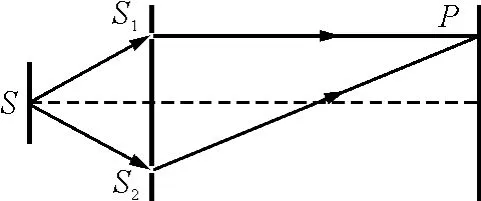
图1 杨氏双孔干涉实验
如图2(a)所示,两波列共有(k+k)个单波和(N-k)个重波到达P点,所以P点的光强为
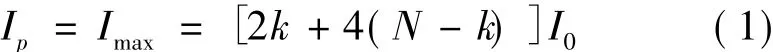
同理,与P点相邻的暗纹P'点的叠加情况如图2(b)所示,两波列中的相干部分为相消干涉,则P'点的光强为
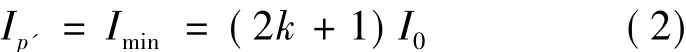
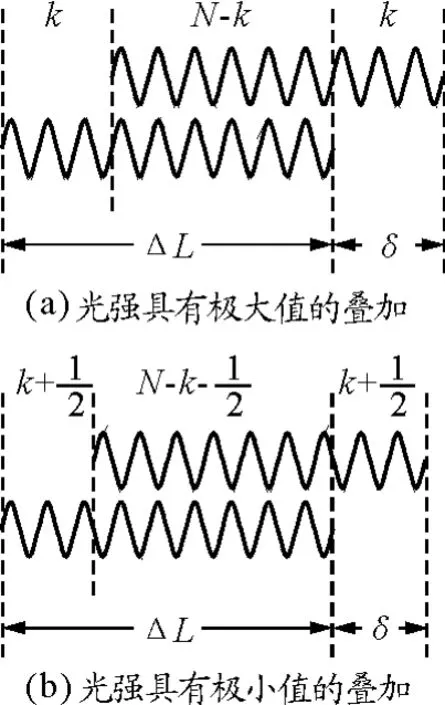
图2 两相干波列的叠加
根据定义,P点附近的可见度为

上式表明,两相干光波叠加时,能产生干涉现象的最大光程差δmax等于光波波列长度ΔL,即相干长度.当准单色光的单色线宽Δλ越小,相干长度ΔL越长,光源的相干性就越好.这种由单色光的单色线宽(或相干长度)所决定的光源的相干性称为时间相干性[3~4].
3 光源的宽度对干涉条纹可见度的影响——空间相干性
严格的点、线光源是不存在的;实际光源上任一点或线都可看成点光源或线光源.每一点和线光源都要产生自己的一套干涉条纹,彼此错开,屏上总强度为各套干涉条纹的非相干叠加[2].
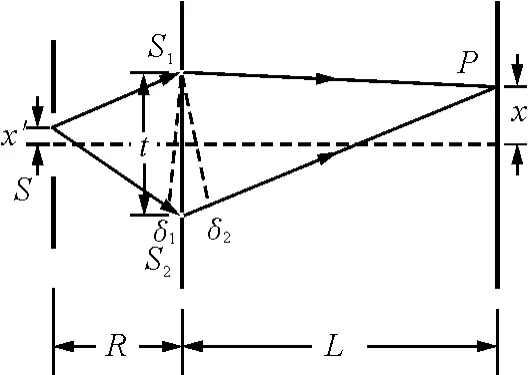
图3 杨氏双缝干涉实验
图3 是杨氏双缝干涉实验示意图.设光源S是缝宽为b的缝源,当R与L均远大于缝间宽度t时,光程差和位相差分别为
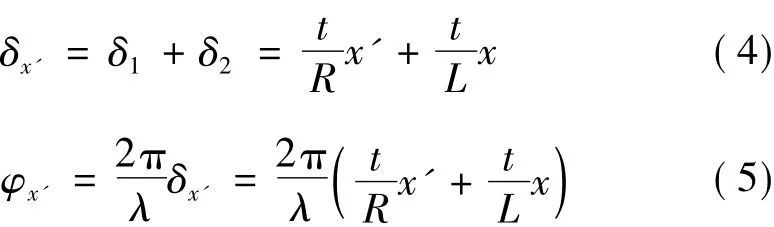
P点的总光强Ip是所有缝元在P点所产生的光强的非相干叠加,即
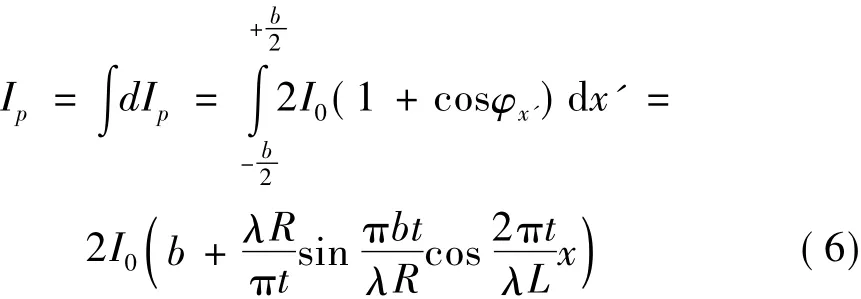
干涉条纹的可见度为

4 普通光源的时空相干度分析
以上是通过杨氏实验讨论光波的时空相干性.实际上,光波的时空相干性是普遍存在的,与实验装置无关.如图4所示,光源S是宽度为b,单色线宽为Δλ的普通光源,光波的中心波长是λ.下面在光源S的光场中确定与给定点O处光波相干的光波所在点的范围,并推导出此范围内各点处的光波与O点处的光波的相干度的计算公式.时,虽然V不一定为零,但起伏较小.所以,通常把θ<也为定值.设C为光场中的任一点,由于光波的空间相干性,光线SC与光线SO的夹角θ必须小于θ0,即C必在顶角为2θ2的 圆锥体中.又因Δλ给定,所以?
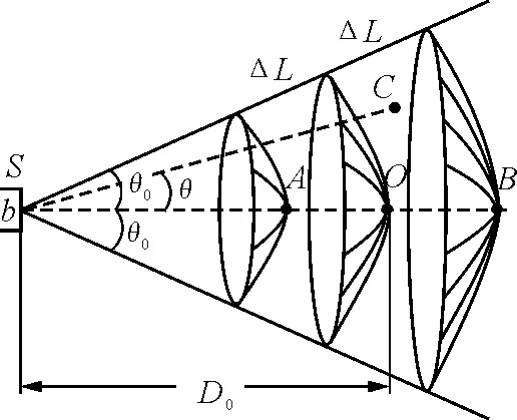
图4 普通光源时空相干示意图
已知b与λ给定,则为定值.由于时间相干性,C点处的光波与O点处的光波的光程差应小于δmax,因此C点必在球冠A与球冠B之间的区域中.
首先讨论线段AB.在此线段上光线SC与光线SO的夹角θ=0,故仅存在时间相干性问题.由于该线段上,C,O两点处的光波的光程差δ<ΔL,因此C,O两点处的光波是相干的.因为两光束的相干度等于其干涉条纹的可见度(γ=V),[5]所以可通过讨论干涉条纹的可见度来讨论光波的相干度.由于线段AB上仅存在时间相干性问题,C,O两点处的光波等光程相遇后产生的干涉条纹的可见度相当于单色线宽为Δλ的点光源在杨氏实验中产生的级干涉条纹的可见度,仅受C,O两点处的光波的光程差δ的影响,即
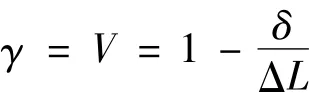
当δ≥ΔL时,即C选在球冠A,B之外(或恰好选在球冠A,B上)时,γ =V=0,说明此时C,O两点处的光波是不相干的.
当0<δ<ΔL时,0<γ=V<1,即C,O两点处的光波是部分相干的.
当δ=0时,γ=V=1,即C,O两点处的光波是完全相干的.
由于线段AB上的任一点处的光波与O点处的光波是相干的,且干涉中仅存在时间相干性问题,称之为O点的相干线域.即当给定光场中一点的相干线域时,则知该线段上的任一点的光波与给定点处的光波是相干的,相干度仅与两点处的光波的光程差有关,即
然后讨论曲面O.在此曲面上,C点处的光波和O点处的光波无光程差,故仅存在空间相干性问题,称之为O点的相干面域.由于该面域位于顶角为2θ0的圆锥体内,即光线SC与光线SO的夹角θ<θ0,故C点处的光波和O点处的光波是相干的,其相干度等于干涉条纹的可见度,仅受光线SC与光线SO的夹角θ的影响,即


δ<1;当θ=0时,即C,O两点重合时,γ=V=1.
最后讨论顶角为2θ0的圆锥体与球冠A,B相交的整个区域.由以上讨论可见,仅有该区域内的光波才与给定点O处的光波相干,称之为相干体域.若给定光场中一点的相干体域,则知该体域内任一点处的光波与给定点处的光波是相干的.其相干度λ与两点对光源中心的夹角θ和两点处光波的光程差δ有关,即
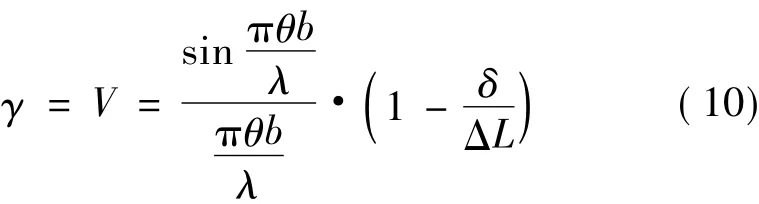
相干体域从整体上反映了光源发出光波时空相干性的好坏;即在D0一定的情况下,相干体域越大,说明该光源发出的光波的时空相干性就越好;反之,光源发出的光波的时空相干性就差.
1 刘坤英,范汝盐.光学.北京:中国科学技术出版社,1994.182~228
2 孔艳,朱益清,朱拓.时间相干性的进一步精确描述.江南大学学报(自然科学版),2003,2(4):421~422
3 田兴时.光学.昆明:云南大学出版社,1996.85~90
4 谢莉莎.光场时间相干性的描述.物理通报,2000(11):9~10
5 吴诗敏.关于两光波干涉条件和相干度的讨论.赣南师范学院学报,1996(6):25~27
