社会防控与信息公开:重大传染病疫情的演化机理与预测模型

赵 宁, 刘德海

(1.东北财经大学 管理科学与工程学院,辽宁 大连 116025; 2.东北财经大学 公共管理学院,辽宁 大连 116025)

0 引言

新冠肺炎疫情蔓延全球，成为世界各国共同面对的公共危机，同时也导致国际社会对各国抗疫模式和国际抗疫合作等产生严重分歧。《柳叶刀》发表社论在肯定了中国为迅速遏制新冠疫情所做出的贡献的同时，也谴责了一些国家应对疫情的疏忽与冷漠[1]。疫情爆发初期，由于缺少疫苗和特效药，社会隔离和主动筛查成为了有效防控疫情的主要措施。而在此过程中，具有权威的公信力、高度的动员能力的政府担任着重要角色。虽然在初期我国地方部门在启动应急响应、协调医疗物资分配等疫情防控工作存在一定的缺陷，但是由于我国政府及时采取了封城、隔离、建立方舱医院等防控措施，截至2020年3月我国疫情基本得到控制，抗击疫情取得阶段性胜利。而反观其他国家，疫情防控却不容乐观[2]，甚至有一些国家将疫情防控作为政治议题，在国际社会对中国抗疫成功经验发起了激烈的指责和抹黑。因此，如何从理论上论证重大传染病疫情初期社会隔离等防控措施的科学性和有效性，成为学术界凝聚国际抗疫合作共识、有效反击他国政客就疫情抹黑中国，所面临的迫切管理实践需求。

从管理学科研究方法的视角，现有对重大公共卫生事件的研究可分为数据研究和数理建模两类。在数据研究公共卫生事件方面，一些学者将系统演化分析等数学模型、亲缘地理学、流行病学调查等多学科方法运用在传染病动力学研究中，分析或预测HIV-1人免疫缺损病毒[3]、1918年西班牙流感病毒[4]和新冠病毒的进化与传播规律[5]。在建立数理模型研究公共卫生事件传播和防控机理方面，一方面，一些文献运用动态平衡模型[6]、传播动力学模型[7]、SWARM系统仿真模型[8]等方法进行重大卫生突发事件的早期预警和预测分析；另一方面，由于突发公共卫生事件防控具有发生的不确定性，发展途径未知性等特点[9]，演化博弈理论为突发公共事件的演化机理与防控机制的研究提供了良好的分析工具[10]。在公共卫生事件方面，李燕凌和丁莹构建政府、网络媒体和公众的演化博弈模型对公共卫生危机中的社会信任修复进行研究[11]。刘德海等根据卫生部公布甲型H1N1流感疫情每日新增确诊病例数，运用演化博弈理论建立了重大突发公共卫生事件的疫情传播方程，对疫情传播初期阶段进行了Logistic方程拟合和疫情传播峰值点的预测分析[12]。但是，文献[12]分析的重点是疫情防控过程中如何权衡“谨慎性”和“灵活性”的矛盾，以及防控措施的最佳调整时机。面对新冠肺炎疫情，我国采取了“群防群控”，“联防联控”的疫情防控模式，取得了显著的抗疫成效，并得到世界卫生组织和国际社会的广泛赞誉。但是，少数西方国家为了回避抗疫不力的责任并企图在国际社会打压中国，不仅指责中国抗疫模式，甚至标榜“群体免疫”等抗疫模式。目前尚缺少文献结合传染病演化机理从理论上论证新冠疫情初期社会隔离等防控措施的科学性和有效性。

在突发疫情的防控过程中，政府的应急处置策略和社会民众的抗议防疫选择都面临着长期的动态调整，各级政府部门之间会彼此借鉴成功的措施和方法，社会公众之间也存在着观察、学习和模仿的过程。不同于现有对传染病预测研究以基本再生数R0衡量疫情扩散状态。本文考虑到在重大传染病防治过程中政府与民众双方采取策略的动态演化特征，结合演化博弈理论分析和数据实证方法，将主动筛查、社区隔离等社会防控措施与传染病自然传播机理结合，构建了基于演化博弈的传染病传播动力学模型，将影响疫情扩散的因素与防控机制等疫情防控因素与经典SI传染病扩散模型参数相结合，分析了重大传染病的社会化演化机理，论证了政府部门采取疫情防控和信息公开措施的实施效果。最后，对三种疫情防控情境下进行Logistic方程拟合和峰值点分析比对，进一步论证了中国疫情防控模式的科学性和有效性。

1 问题描述与基本假设

面对新型病毒，在高度不确定性的决策条件下，各国政府的防控策略和社会民众的策略选择都存在着模仿和试错行为。对各国政府而言，随着疫情防控的推进和复工复产的强烈要求，疫情防控策略也随之不断调整。因此，各国政府和民众在疫情初期均采取适应性的学习行为[12]；对社会群体而言，在疫情初期病毒的传播率和致病致死率等信息缺位的情况下，谣言和恐慌心理会共同影响社会群体的决策，民众倾向于逃离疫区[13]。此外，尽管在疫情初期，实行交通管控、居家隔离等防控措施可以有效应对疫情，但同时也会给地方政府和民众带来诸多不便。对地方政府而言，采取疫情防控措施必将导致当地旅游人数下降、招商引资工作停顿，进而影响经济发展，给政府带来较大的经济损失；对民众而言，居家隔离不仅会给日常生活带来诸多不便，误工停工还会直接影响民众的经济收益，在疫情爆发初期缺少政策补贴和辅助措施的情况下，民众也会因居家隔离而承受一定的经济损失。

2 重大传染病疫情防控机理的演化博弈模型

2.1 要素博弈

新冠病毒具有极强的传染性，但在疫情发生初期，并没有引起地方政府部门足够的重视[14]。本文采取图1所示的要素博弈收益矩阵，表示在疫情爆发和扩散的初期阶段，地方政府部门和社会公众双方作为两个不同群体进行的博弈。其中，政府部门采取强制干预措施T后对地方经济发展的负面影响为(-v);而包括患者在内的社会公众自觉地在所在单位(或居民区)就地隔离Q而导致的误工误学以及其他生活方面的损失为(-c)，相应地，群众配合隔离下，地方政府收到抗疫收益g；如果政府部门采取强制干预措施后社会公众仍坚持外逃流动H，则政府部门采取罚款、行政处分，甚至追究刑事责任等措施，对社会公众外逃流动造成扩散的惩罚为(-p)。为了使政府部门采取的强制干预措施有效，显然，p>c。

分析图1要素博弈的收益矩阵可知，在疫情爆发的初期阶段，出于上述各种原因的考虑，博弈的纳什均衡是{逃离疫区H，不作为D}，从而造成在更大范围内疫情的传播。

社会公众政府部门强制干预T不作为D逃离疫区H-p,-v0,0就地隔离Q-c,g-v-c,g

2.2 重大传染病疫情初期的自然扩散模型

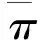
(1)

更进一步，考虑到信息披露和传播过程中存在着各种障碍或限制，导致了一些更为关键的策略或信息更难以被观察或学习。不同策略存在着相应行动被观察到的可能性(用λ表示)差异，一些策略可能更难于被观察，因此也更难于学习[16]。因此，其扩散方程可以表示为:

(2)

结论1在疫情初期阶段，疫情扩散速度与群体中采取流动策略的比例和流动行为可被观测到概率相关。如果政府部门未能及时采取隔离措施并公开疫情防控工作的精准信息，由于信息缺位而导致的恐慌和盲从心理将加剧疫区居民的逃离行为。

由于政府信息不公开反而造成了非正规渠道下λi的增大，进一步加剧了疫情的扩散蔓延。政府部门一方面采取有效的隔离措施，减少了采取流动策略的比例θi(t)，进而减少了交叉感染的概率；另一方面通过一系列信息公开措施，降低了社会公众的恐慌心理，λi的减少降低了疫情扩散速度。

2.3 重大传染病疫情后期的社会防控模型

在疫情防控机制正式启动后，政府部门实行强有力的管控措施。本节在此基础之上构建如图2的要素博弈收益矩阵。启动行政问责制后，玩忽职守的行政官员受到相应责罚，其损失为(-w)，显然，w>v；政府部门对患者提供免费医疗，社区物业等部门也为居民区住户提供便捷服务，降低了社会公众就地隔离的损失(-c)；针对疫情期间受影响的服务行业，推出减免行政事业性收费措施，降低了地方政府采取强制干预措施时遇到的阻力(-v)；对妨碍疫情工作防控的行为依法制裁，提高对四疑流窜人员的处罚(-p)，为了保证干预措施的有效性，p>c。即公众如果不配合会受到严厉的惩罚。给定上述参数关系，分析图2要素博弈的收益矩阵可知，随着各级政府采取严厉的管控措施，促使疫情防控尽快出现转折点。在疫情后期控制阶段，博弈的纳什均衡转化为社会公众的就地隔离和政府部门的强制干预(Q，T)，疫情得到有效控制并缓解。

社会公众政府部门强制干预T不作为D流动行为H-p,-v0,-w就地隔离Q-c,g-v-c,g-w

由图2要素博弈收益矩阵所示，各级政府采取上述一系列调整措施后，一方面，政府官员面对疫情不作为现象将付出极大的成本，另一方面社会公众经过宣传动员后采取自我居家隔离措施，减少人员流动。调整后的期间应急机制(政府部门强制干预，社会公众就地隔离)，逐渐演化成为稳定的均衡。因此，疫情收敛的动态过程可以通过θi(t)的递减来间接地加以表示。此时，社会公众采取就地隔离的行动Q(记为策略j)将预期获得更大效用，其收敛方程可以表示为：

(3)

由πj>πi可知，(3)式中dθi(t)/dt<0，拒绝隔离的公众数量逐渐减少，在重大传染病等社会公共卫生突发事件后期将逐渐收敛到新体制下稳定的认知均衡点(Q，T)。

结论2在疫情扩散中后期收敛阶段，疫情的收敛速度与公众隔离与否所得收益差值和主动隔离行为被观察到的可能性成负相关。政府应采取强力的干预措施，从惩治防控不利部门和对公众进步防疫补贴两方面入手，通过改变决策收益的方式影响均衡结果，达成政府部门“强制干预”社会公众“就地隔离”的均衡结果。

分析式3可知，重大传染病等社会公共卫生突发事件后期的收敛速度，主要取决于如下两点因素：第一，社会公众采取不同策略的预期效用差。政府部门通过启动社会公共卫生系统的应急机制，通过改变危机期间社会公众和各级政府官员采取不同行动的预期收益，从而有效控制了疫情扩散速度。第二，居家隔离的可能性。政府部门通过新闻媒体进行有效的引导，提倡居家隔离，从而有效地控制疫情的蔓延趋势，加大了疫情后期的收敛速度。

3 考虑社会防控的重大传染病疫情演化博弈预测模型

3.1 重大传染病疫情预测的演化博弈理论模型

重大传染病疫情初期传播由于缺少疫苗等有效防控手段，基本符合经典的传染病传播SI模型。但是，该模型并不能反映出疫情初期基于公共卫生系统采取社会防控措施的影响。根据初期扩散方程式(2)，可得：

dθi(t)/dt=λiθi(t)(1-θi(t))(πi-πj)

(4)

上式即为传染病扩散SI方程(即Logistic增长模型)。

dI(t)/dt=I(t)(1-(t))η

(5)

本文结合传染病防控过程中的政府角色，将演化博弈理论与Logistic增长模型相结合。在Logistic自我抑制增长模型中，待估参数b1用于衡量增长速度的快慢。本文将其内生化，采取流窜策略群体被观测的概率、疾病最大感染人数K和是否配合隔离的收益差值πi-πj共同刻画社会防控措施的综合影响。

3.2 情景1：政府隐瞒信息防控乏力，民众漠视下的疫情大规模扩散

由于试剂污染和美国政客刻意放缓检测速度等因素影响，在疫情爆发中后期美国病例数据已经不具有真实性，本文选取2020年2月12日至4月2日期间疫情爆发初期美国每日新增病例数据进行拟合(数据来源于央视新闻、人民日报等权威媒体)，并通过试错法设定累计确诊病例上限K值。其中，当K=30000000时新冠肺炎频数演化方程获得了最好的拟合效果，拟合结果如图3所示，可得美国累计确诊病例数的频数拟合方程为:

(6)

其中，Logistic回归的可决系数为0.993，即截至2020年4月12日美国累计确诊病例数97%以上的变动可以由该模型解释，拟合优度较高；F统计量为1756.208，对应p值为0，该模型整体显著。

图3中疫情爆发初期确诊病例数高于拟合曲线。这是由于新冠病毒一般具有3～7天左右的潜伏期，因此导致了潜伏期过后确诊病例数的集中爆发。美国政府在初期的防疫过程中，不但并没有做到信息透明公开，反而停止公布全国检测人数、以及检测结果为阴性的人数，延误了控制疫情的最佳时机。美国联邦政府又在应对措施刚开始取得成果之时，急于通过取消隔离限制来提振经济，最终导致人群间采取自由流窜策略可被观测的概率增大。在疫情事态恶化之时，第49天后确诊病例数略低于拟合曲线，这是由于美国各州检测条件和费用等限制，没有做到应检尽检。根据拟合方程(6),当t=139.4时，每日新增病例数为1，即2020年7月1日美国受感染人数将达到3000万。而根据美国疾病控制与预防中心主任罗伯特·雷德菲尔德的估计，实际上，截至当地时间6月25日，已经有超过2300万人感染新冠肺炎。

图3 美国新冠肺炎累计确诊病例Logistic曲线拟合图和参数估计

3.3 情景2：政府积极防控，民众初期拒绝配合下的疫情扩散

欧洲国家有长期的自由传统，政府的社会控制能力不足。除此之外，政府在初期防控并没有对民众进行有效的补贴。因此民众拒绝配合政府的防疫举措。本文选取2020年2月8日至3月28日期间意大利每日新增病例数据进行拟合(数据来源于央视新闻、人民日报等权威媒体)，通过试错法，发现当K=240000时新冠肺炎频数演化方程获得了最好的拟合效果，拟合结果如图4所示。可得意大利累计确诊病例数的频数拟合方程为:

(7)

图4 意大利新冠肺炎累计确诊病例Logistic曲线拟合图和参数估计

其中，Logistic回归的可决系数为0.939，即截止2020年3月28日意大利累计确诊病例数93.9%以上的变动可以由该模型解释，拟合优度较高；F统计量为735.499，对应p值为0，该模型是整体显著的。在意大利民众防疫配合程度较差的演化情景下，根据拟合方程(7),当t=93.1时，每日新增病例数为1，即2020年5月10日意大利受感染人数将达到峰值24万。

图4显示了意大利的疫情演化图。由于新冠病毒一般具有3～7天左右的潜伏期，疫情爆发初期确诊病例数高于拟合曲线。在2020年3月初，面对严峻的疫情形势，意大利政府出台了一系列有力的防疫措施。考虑到新冠肺炎具有半个月左右的潜伏期，3月18日拐点出现之时，正是一系列抗疫措施实施后半个月左右的时间。这也恰恰反映了在抗疫过程中政府采取强力封闭措施的重要性。根据我们的预测，意大利疫情将在2020年5月10日达到感染峰值24万。事实上意大利疫情在六月末左右达到了24万。峰值出现时间推后的主要原因，除了检测能力的局限外，另一个原因是意大利政府在后期抗疫中充分借鉴我国成功经验。

3.4 情景3：政府积极防控，民众配合隔离，疫情被迅速扼制

我国政府坚持把人民群众生命安全和身体健康放在第一位，逐步推进疫情防控工作。3月6日，多省实现“清零”，疫情得到了较好的控制。虽然局部地区也会因防控松懈出现聚集性感染的现象，但是也都在可防可控范围之内。本文选取2020年1月20日至2020年3月8日期间卫健委官方网站通报的每日新增病例数据进行拟合，通过试错法，设定累计确诊病例上限K值。其中，当K=82000时新冠肺炎频数演化方程获得了最好的拟合效果，拟合结果如图5所示。可得中国计确诊病例数的频数拟合方程为:

(8)

其中，Logistic回归的可决系数为0.946，即截止2020年3月8日中国累计确诊病例数94%变动可以由该模型解释，拟合优度较高；F统计量为802.545，对应p值为0，该模型是整体显著的。根据方程(8)，当t=75.5时，每日新增病例数为1，即2020年4月3日中国累计受感染人数将达到峰值8.2万。

分析图5，我国积极防控下的疫情演化图，与Logistic回归模型(8)理论值相比，在第24天，也就是2020年2月12日出现了较大的偏差。其原因当天放宽了检测标准导致单日新增病例变多。但是，Logistic回归方程的峰值点预测与实际情况吻合较好，验证了理论模型具有较好的实用性。而根据国家卫健委通报，截至4月3日，我国累计确诊病例为81639人，本文预测结果与现实基本相符。

图5 中国新冠肺炎累计确诊病例Logistic曲线拟合图和参数估计

4 结论

尽管中国政府自新冠疫情爆发之初积极向世界分享抗疫经验，但是新冠疫情仍然接连席卷世界各国。面对疫情威胁，一些国家和政客甚至将疫情防控政治化操作，标榜“群体免疫”模式，抹黑中国抗疫的成功经验。如何从理论上论证中国疫情防控措施的重要作用，是当前学术界面临着迫切的现实需求和挑战。

本文基于传染病传播机理进一步考虑了社会防控等因素，将演化博弈理论与传染病SI模型相结合，揭示了重大传染扩散传播的社会防控机制。最后，分析了政府部门采取的控制措施和信息公开措施在疫情防治中的作用。政府部门采取了强制干预措施后，改变了演化博弈中的要素博弈收益矩阵，从而使得博弈均衡发生演化。在原演化博弈模型中在无限期收敛的动态过程，变为有限期终止的、经历扩散和收敛两个发展阶段的动态过程。因此，新的扩散和收敛模型具有更强的现实解释力。在疫情防治工作初期，政府部门采取管制交通和信息公开措施后，一方面降低了社会公众的恐慌心里，减少了扩散方程中社会公众选择“外逃流动”策略的可观察性，有利于抑制疫情的扩散；在疫情防治的中后期阶段，中央政府启动政府官员行政问责制，加大了对政府官员防治工作不力的惩罚力度，同时出台一系列税收，保险以及补偿政策，补贴公众居家隔离期间所承受的损失，使要素博弈中的原纳什均衡(公众外逃流动，政府不作为)演化为新的纳什均衡(公众就地隔离，政府强制干预)，从而成为重大传染病等社会公共卫生突发事件防治工作的转折点，加快了疫情的收敛。通过对美国，意大利和我国三种疫情防控情境下的演化预测比较分析，论证了在疫情初期果断地采取包括政府疫情信息公开、社会充分动员和主动隔离的中国抗疫模式是疫情防控的有效手段。

本文考虑关于疫情真实可靠的科学信息仅能够通过政府部门向社会公众进行披露，但是随着信息技术的发展和普及，大数据技术的广泛应用和新媒体平台的普及，社会群体也有可能通过信息搜索的途径在第一时间获取疫情相关的科学信息。另外，在新冠肺炎疫情演变为全球大流行病的背景下，需要整合多学科，不仅包括流行病学，还包括社会科学、研究与开发、物流和危机管理等多学科的交流融合。在新冠肺炎疫情的挑战下，中方作为世卫组织国际卫生条例的缔约国，始终本着公开、透明、负责任的态度，采取了最全面、最严格、最彻底的举措，中国政府和人民克服巨大困难，付出了巨大的牺牲，做好了疫情的防控。我们在做好自身防控工作的同时，更应该思考如何跨越体制和文化的深层隔阂，为降低疫情的国际传播履行应尽的义务。