面向绿色智能制造的高维多目标动态作业车间调度优化
2023-03-02周双牛
李 稚, 周双牛
(天津工业大学 经济与管理学院,天津 300387)
0 引言
国务院于2015年部署“中国制造2025”战略,提出把绿色发展作为主攻方向之一,构建高效、低碳、循环的绿色制造体系,以自动化技术、信息技术为核心的先进制造技术推动我国制造业向智能化和绿色化方向发展。十九大报告提出“生态优先、绿色发展”的制造业发展理念,指导制造企业绿色转型升级,以实现可持续发展战略目标。基于此,绿色发展理念在人工智能和大数据背景下,工业化与信息化的融合,催生了新的工业发展形态——绿色智能制造,即基于新一代信息技术与制造技术深度融合,将环保理念应用于生产制造活动中,实现节能减排的新型制造模式[1,2]。绿色智能制造深刻改变了传统制造企业的生产模式,如何面对智能化生产转型和升级,绿色智能车间的建立及运营是关键。柔性作业车间调度是绿色智能制造的核心问题,需要综合考虑环境、指标等多个相冲突目标,在资源约束条件下提出一系列绿色低碳的作业车间调度方案。高效智能的调度策略能够优化企业的生产运作管理,助力我国绿色智能制造业的稳健发展。
近年来,有学者初涉绿色作业车间调度领域研究。李益兵等[3]提出从碳排放量、噪声及废弃物三个方面综合评定环境污染等级,建立以极小化最大完工时间和环境污染程度为目标的多目标绿色柔性作业车间调度模型;刘彩洁等[4]考虑分时电价政策,建立以极小化最大完工时间、碳排放和能耗成本的绿色柔性作业车间调度多目标优化模型,实现了时间、经济和能耗三者的协同优化;李聪波等[5]对机床加工过程中消耗的直接能源和间接能源进行研究,提出广义能耗概念,建立能耗多目标优化模型,并开发模拟退火算法对柔性作业车间调度模型求解。以上研究主要对环境污染或能源消耗方面进行分析,在研究目标中加入绿色指标,但约束条件尚未考虑绿色约束。研究得到的优化解,大多是在传统车间调度问题结果中选出绿色指标较优的方案。然而,在实际绿色柔性作业车间调度过程中需要全方面考虑绿色因素,即在目标函数和约束条件中均涉及绿色指标。显然,现有研究在绿色柔性作业车间调度模型构建方面具有一定局限性。
多目标柔性作业车间调度问题,现有研究主要基于Pareto寻优的方法[6]直接在多目标空间中寻优,其中非支配排序遗传算法[7]和多目标粒子群算法[8]是比较成熟和理想的Pareto寻优算法。Komaki等[9]首次将灰狼优化(Grey Wolf Optimizer, GWO)算法应用于生产调度问题,实验表明GWO算法优于其他元启发式算法,然而该研究是对GWO算法的简单应用,并未解决复杂生产调度问题;Tawhid等[10]运用差分进化对GWO算法中包围猎物操作进行改进,但改进后的算法只适合用于连续型问题的求解。柔性作业车间调度问题具有复杂性,目前研究目标主要集中于最大完工时间、成本、机器负荷等生产指标,由于求解算法的局限性,现有研究大多同时考虑2~3个目标,关注目标较少。高维多目标柔性作业车间调度是实际生产作业的真实反映。目前,鲜有研究将总能耗等绿色指标纳入多目标模型构建中,并同时考虑4个及以上目标的高维多目标[11]柔性作业车间调度问题。
综上,现有文献大多关注最大完工时间的优化问题,而忽略实际生产中其他重要因素,如污染排放、机器负荷、产品质量等。也有学者只针对绿色作业车间调度或者动态调度问题进行单一维度研究,尚未发现将二者结合进行多维度柔性车间调度研究。基于此,本文开发高效智能优化算法——改进的多目标灰狼优化算法(Improved Multi-objective Grey Wolf Optimizer, IMOGWO)对高维多目标绿色动态柔性作业车间调度问题(Many Objective Green Dynamic Flexible Job-shop Scheduling Problem, MaO-GDFJSP)进行求解,提出最优的作业车间调度方案。本研究主要创新点为:(1)考虑不同机器状态下的能耗情况,以及机器使用节能方法,建立了基于机器故障,研究总能耗、最大完工时间、机器总负荷和产品质量稳定性的高维4目标的MaO-GDFJSP模型;(2)创造性地提出多级官员领导机制,将灰狼种群改为多层多级结构,有利于扩大种群多样性;(3)将遗传算法中优秀因子引入灰狼算法,如POX交叉算子、逆转算子,尤其是依据Pareto解集提出自适应精英保留策略,提高了种群更新效率和质量。
1 MaO-GDFJSP模型的建立
1.1 MaO-GDFJSP的描述
MaO-GDFJSP是绿色制造的重要问题。MaO-GDFJSP问题描述:车间有n个工件需要在m台机器上进行加工,其中每个工件有ni道工序,每道工序的可选加工机器集Mij及其加工时间已知。MaO-GDFJSP问题基于绿色调度和动态调度,对生产加工中的多个目标进行综合决策以寻找满足复杂条件的调度方案。选取生产加工中常用的极小化总能耗、最大完工时间、机器总负荷和产品质量稳定性4个目标。此外,还需考虑以下假设条件:
(1)在初始时刻所有工件处于待加工状态,所有机器处于空闲状态;
(2)同一时刻,每台机器只能加工一个工件,每个工件只能被一台机器所加工;
(3)工件加工过程中不能中断;
(4)同一工件不同工序之间有先后顺序,不同工件之间无先后顺序;
(5)忽略机器启动及换型时间、工件运输时间及重调度计算时间[12]。
1.2 数学模型的建立
为描述问题方便,定义符号及其含义如下(见表1)。

表1 主要符号及其说明
在前人对动态车间调度和多目标车间调度问题基础上,建立适合MaO-GDFJSP的混合整数规划模型,表示为min(E,T,L,Q)。
(1)总能耗E是绿色智能制造下需要考虑的重要指标。在实际生产中,总能耗可分为加工能耗和空载能耗,加工能耗是指机器加工工件时所消耗的能量,如式(2)所示;空载能耗是指在下一工件到达之前机器空转所消耗的能量,如式(3)所示。
(1)
(2)
Eq=[max(Xijh×Fijh)-min(Xijh×Sijh)-
(3)
(2)最大完工时间T是车间调度问题中评价生产效率的重要指标,如式(4)所示。在动态调度中需要对机器故障的修复时间进行考虑,机器正常工作情况下各工序的加工结束时间如式(5),机器故障情况下各工序的加工结束时间如式(6)所示。
T=maxFijh
(4)
Fijh=Sijh+Pijh
(5)
Fijh=Sijh+Pijh+Rh
(6)
(3)机器总负荷L是零件在机器上加工的总时间,机器总负荷对机器寿命产生严重影响。
(7)
(4)产品质量稳定性指数Q是制造业企业生存的命脉,不同的机器生产出的产品质量不同,可以用不合格品率表示,不合格品率越低,加工质量越稳定。加工后期出现产品质量问题的成本要远高于前期,因此用工序质量不稳定指数aijh来表示,如式(8)所示。
(8)
另外,MaO-GDFJSP需要满足的约束条件如下:
Fijh×Xijh=Sijh×Xijh+Pijh
(9)
(10)
Fijh≤Si(j+1)h
(11)
Fxyh×Xxyh≤Sijh×Xijh,(Sijh≥Sxyh)
(12)
Fijh×Xijh≤Sxyh×Xxyh,(Sijh≤Sxyh)
(13)
FTh=max(Xijh×Fijh)-FMh
(14)
其中,式(9)表示工件一旦加工中途不能中断;式(10)表示每道工序只能被加工一次;式(11)表示表示同一工件的不同工序之间有先后顺序;式(12)和式(13)表示同一时刻,一台机器只能加工一个工件;式(14)表示一台机器加工完本机器所有任务的提前关机时间。
3 高维多目标动态柔性作业车间调度问题的IMOGWO算法
3.1 多目标优化问题描述
多目标优化问题(Multi-objective Optimization Problem, MOP)是在多个目标函数F=(f1,f2,…,fr)下求解决策变量X=(x1,x2,…,xm),MOP往往包含多个相互冲突的目标函数,故其最优解变为包含多个决策变量的最优解集。对于给定向量X,Y∈R,当且仅当∀j∈{1,2,…,m},xi 3.2.1 MSOS编码 染色体编码会影响优化算法的求解效率,本节选取MSOS[13]编码方法。此方法将个体分为机器选择串(Machines Selection, MS)和工序选择串(Operations Sequence, OS),分别用以解决路径子问题和调度子问题,如图1所示。MS和OS的长度均为总工序数,MS按工序编号依次排列,每个基因座由该工序可选机器集的顺序号表示,如工序O22的机器集有{M1,M2,M3},2表示此机器集中第二个机器M2。OS用工件号进行表示,工件i出现的第j次,表示工序Oij。 图1 MSOS编码示意图 3.2.2 反向学习初始化种群策略 3.2.3 多级官员领导机制 由于标准GWO算法容易陷入局部最优,依据多目标优化算法最优解的特点提出多级官员领导机制,改善标准GWO算法中一级多层的结构,进而扩大种群多样性。多级官员领导机制引入国家(Country)、省(Province)和地级市(Prefecture level city)的政治组织结构,每一级均设有α,β和δ层。从高到低依次为C级、P级和Plc级,每一级内α>β>δ,如图2所示。确定各级领导的具体操作步骤如下: 图2 多级官员领导机制更新示意图 Step1对Pareto解集不断进行非支配排序并反向标号; Step2对每一层Pareto解,计算拥挤距离并再次标号; Step3从第一层Pareto解集开始,按标号依次将灰狼个体取出,直到满足9个个体; Step4将9个个体依次分配到Cα、Cβ、Cδ、Pα、Pβ、Pδ、Plcα、Plcβ和plcδ,将剩余个体作为ω层。 3.2.4 POX交叉 交叉算子能够探索未知空间,扩大种群多样性,起到全局搜索的作用。本节采用POX交叉算子[15],染色体进行POX交叉操作后仍是可行解,大大提高了算法求解效率。以3个工件,每个工件3道工序为例,如图3所示,POX交叉算子的操作步骤如下: Step1将两条染色体作为父代,记为P1和P2,将两条空染色体作为子代,记为C1和C2; Step2将所有工件随机划分到两个集合中,记为J1和J2,并满足J1∪J2和J1∩J2=Ø; Step3将P1和P2中的J1元素分别复制到C1和C2中的对应基因位; Step4将P1中的J2元素依次复制到C2的空基因位,将P2中的J2元素依次复制到C1的空基因位上,并调整加工机器。 图3 POX交叉示意图 3.2.5 逆序变异算子 在算法迭代后期,对个体进行逆序变异操作能够保留父代的优秀基因,增强搜索精度,改善算法的局部搜索能力。逆序变异的操作步骤为:首先,选择一条染色体P;然后,随机选择两个基因位,将两个基因位之间的所有基因取出并翻转;最后插入到基因位断裂处。 3.2.6 改进精英保留策略 根据多目标优化算法最优解集的特点,提出改进的精英保留策略。IMOGWO每一代的求解结果为Pareto最优解集,对其循环进行非支配排序,直到最后一层所有解互不占优,从后往前对每一层最优解集进行标号。传统精英保留策略采用固定比例对种群进行保留,改进的精英保留策略使用自适应机制,保留每代种群的前k层Pareto最优解集,使用反向种群初始化策略生成g个个体,保持种群规模不变,k和g的公式如下,其中⎣x」表示对x向上取整,N为种群规模,gen为当前迭代次数,maxgen为最大迭代次数。 (15) (16) 为解决高维多目标离散型问题,对标准GWO算法进行改进。改进之处主要包括:离散型编码、反向学习初始化种群策略、POX交叉算子、逆序变异算子、多级官员领导机制以及精英保留策略,IMOGWO算法流程如图4所示。 图4 IMOGWO算法流程图 为验证IMOGWO算法求解MaO-GDFJSP的性能,设计两组实验。第一组在OR-Library中选取11个经典的作业车间调度测试数据集进行求解。相关参数设置为:机器空载功率为[1,10]的随机数,机器加工功率为[10,30]的随机数,工序质量不稳定性指数为[0,0.3]的随机数。第二组实验对某加工车间的加工数据进行仿真,验证IMOGWO算法求解MaO-GDFJSP的有效性。选取多目标粒子群算法MOPSO和未改进多目标灰狼算法MOGWO进行对比。为保证对比实验的科学性,保持三种算法共同参数一致:最大迭代次数maxgen=100,种群规模n=100,MOPSO算法中的c1=c2=1.4962,w=0.7298,MOGWO算法中的a=2。 为便于比较不同多目标优化算法的求解性能,采用SP测度和GD测度[16]对三种算法的性能进行评判。测试算例选取3个FT类基准问题和8个LA类基准问题。将三种优化算法分别对每个测试问题求解20次,每运行一次获得一组[SP,GD]指标值,求SP测度和GD测度的平均值,三种优化算法求解结果如表2所示,每项指标的最优结果用粗体标识。 表2 11个测试算例的三种算法性能对比 由表2可知,在SP测度方面,IMOGWO算法在10个算例中取得最优结果,表明其相较于另外两种算法具有很好的分布性,此外MOGWO算法比MOPSO算法分布性要好。在GD测度方面,IMOGWO算法同样取得10个算例的最优结果,表明三种算法中IMOGWO具有良好的收敛性;相较而言,MOPSO算法的收敛性优于MOGWO算法。 运用IMOGWO算法对实际生产企业车间绿色调度问题进行求解,引用陈超等[17]中6个工件10台机器。假设机器3在30min时发生故障的加工实例,三种智能优化算法分别对其运行20次,求得4个目标的最优解如表3所示,三种算法求解的甘特图如图5所示,Pareto前端四维图如图6所示,其中第四维度用颜色表示其大小。由表3可知,IMOGWO算法能够在总能耗最小情况下保证其他3个目标最优,求解性能优于另外两个算法。而MOGWO算法只在机器总负荷方面优于MOPSO算法。表3表明改进后的IMOGWO算法在高维多目标问题的求解上性能更优。 表3 三种算法求解MaO-GDFJSP结果表 (a)IMOGWO求解甘特图 (b)MOGWO算法求解甘特图 (c)MOPSO算法求解甘特图图5 三种算法求解的甘特图 图5(a)~(c)表示三种算法求解MaO-GDFJSP实例的加工方案,不同颜色代表不同的工件,红线表示在30分钟时机器3发生故障,后续工序需进行重调度。对比图5(a)~(c)可知,在总能耗、最大完工时间、机器总负荷及产品质量稳定性方面,IMOGWO算法比MOGWO算法和MOPSO算法分别提高(12.6%,13.3%,1.6%,11.5%)和(4.5%,6.6%,2.1%,7.7%),进一步说明IMOGWO算法求解高维多目标问题的优越性,能够保证每个目标达到最优。 (a)IMOGWO前端 (b)MOGWO前端 (c)MOPSO前端图6 三种算法的Pareto前端四维图 图6(a)~(c)是三种算法Pareto最优解集的可视化,能够对多目标算法的求解性能进行直观比较。对非劣解分布性进行分析,对比图6(a)~(c),IMOGWO算法非劣解的分布性最优,非劣解沿着Pareto前端均匀伸展,MOGWO算法求得的非劣解在L<190区域的分布极不均匀,MOPSO算法非劣解的分布性最差,在L<190和T<70的区域非劣解数量极少且分布离散,MOPSO算法易进入局部最优困境,与表2结论一致。由此得出,IMOGWO算法在处理高维多目标问题时能够求解更多非劣解,并且Pareto前端的分布性更好。 在绿色智能制造背景下,本文分析了不同机器状态下的能耗情况和机器使用节能方法,以总能耗、最短完工时间、机器总负荷和产品质量稳定性为优化目标,建立基于绿色调度和动态调度的MaO-GDFJSP模型,并设计IMOGWO算法进行求解。该算法以标准GWO算法为基础,使用MSOS编码以求解离散型问题。用反向学习初始化种群策略扩大种群多样性,引入POX交叉和逆序变异算子对灰狼个体进行更新,创造性地提出了基于多级官员领导机制,设计自适应精英保留策略,使之适用于多目标优化算法,能够增强算法的收敛性。 本研究结论得到管理启示:(1)算法应用方面,提出的IMOGWO算法通过工序合理排序同时优化多个目标,可为企业生产作业提供绿色排产方法,实现企业向低耗能和智能化的现代化生产转变。(2)算法升级方面,“多品种,小批量,低耗能”已成为企业绿色生产的特点,制造企业现有的排产算法也需改进升级。因此可基于本文算法改进思路开发出更符合实际生产的排产系统,为制造企业绿色智能化转型升级赋能。(3)成果推广方面,近年来,为了应对日益加剧的环境问题,我国政府不断出台碳排放相关政策,如碳交易、强制减排、碳税制度等[18]。企业在关注生产制造过程节能减排的同时,可以将IMOGWO算法思想应用到绿色产品研发、管理服务等制造活动各个环节,实现产品全生命周期“绿色化”和“智能化”双升级。3.2 改进多目标灰狼优化(IMOGWO)算法设计


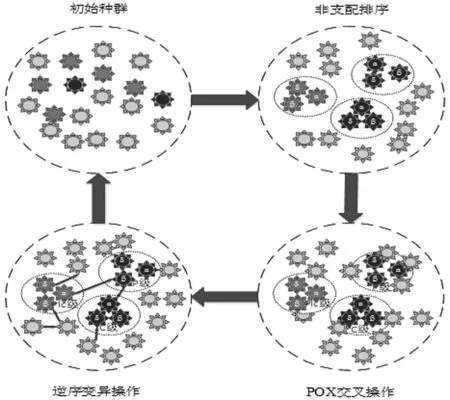

3.3 改进多目标灰狼优化(IMOGWO)算法的实现
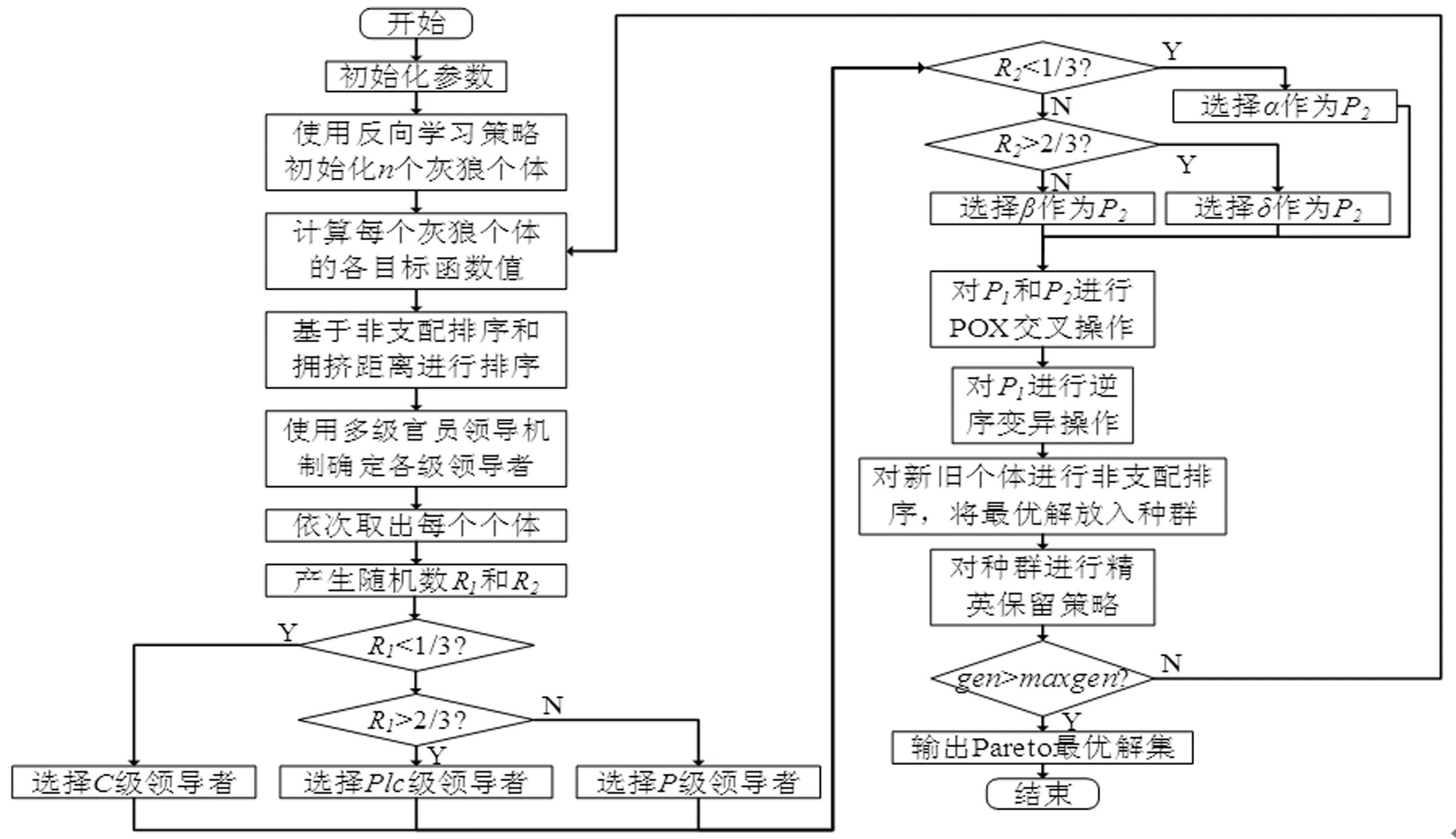
4 仿真实验与分析
4.1 标准算例仿真实验结果及分析

4.2 MaO-GDFJSP仿真结果及分析
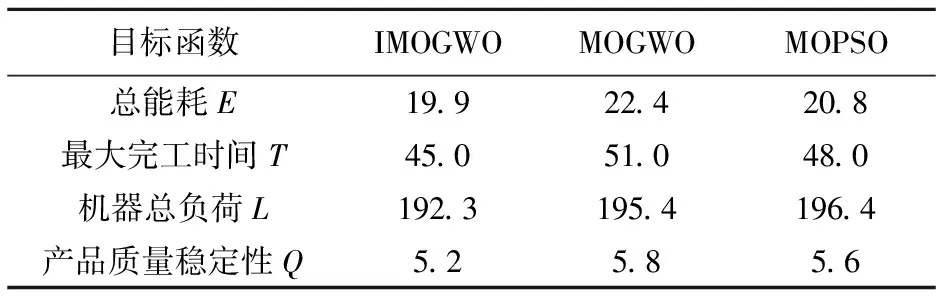


5 结论与启示
