事件故障状态量子博弈过程的参与者收益研究

崔铁军, 李莎莎

(1.辽宁工程技术大学 安全科学与工程学院,辽宁 葫芦岛 125105; 2.辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105)

0 引言

量子博弈过程的特点是将系统状态及参与者的策略等表示为量子态形式。这样可将博弈过程中各种参与者行为的博弈过程充分展示，即参与者采用不同策略对收益的影响。利用量子态表示了多种参与者的多种行为对于收益变化的作用和影响。实际上，对于事件而言，将事件是否安全完成作为目标，参与者也可分为两派，拥有并管理事件的管理者及具体操作完成事件的操作者。双方也有各自的安全行为和不安全行为。当然双方采取不同行为给自身带来的事件完成后的收益也不同。他们的安全和不安全行为策略组合有四种状态。按照一般的博弈论，双方都采用安全行为必将获得最大收益；都采取不安全行为受益最小；但双方之一采用不安全行为，另一方采用安全行为则收益更小。进一步的，当双方有信息通讯时可调整各自策略，无信息通讯时只能各自完成策略。因此对于事件故障状态的分析，即是双方的博弈过程，也是有无信息通信的量子纠缠过程。那么由众多事件组成的系统故障演化过程的系统故障状态与这些事件的故障状态有密切关系。因此在研究系统故障状态之前必须了解事件故障状态，并进行描述和分析。

相关事件和系统的故障状态研究目前已出现一些。较新的包括量子态与故障状态的研究，例如EEMD能量矩和改进量子粒子群神经网络的故障诊断[1]，AQPSO-LSTM-BN的APU故障诊断[2]，量子计算和免疫优化结合的电网故障定位[3]，多尺度量子熵的信号故障特征提取[4]，机械故障稀疏特征相似性度量优化[5]；博弈方法与故障状态的研究，例如主从博弈理论的电网多能互补协调故障研究[6]，博弈论综合法的城市供电系统安全[7]，合作博弈的电网支路脆弱性研究[8]，考虑共因故障的系统组成单元故障分析[9]，完全信息序贯博弈模型的变压器保护策略[10]；智能分析方法与故障状态的研究，例如灰色关联理论下的移动机器人故障诊断[11]，故障本征证据和特征指标的变压器故障状态研究[12]，轴承故障的排列熵特征提取与模糊识别[13]，改进残差神经网络的滚动轴承故障诊断[14]，扩张状态观测器的运输机多故障容错研究[15]，供应链中损失和浪费的量子博弈方法[16]，基于量子博弈安全性的密码分析与改进[17]，量子博弈在信息通讯加密方面的研究[18]，使用量子博弈的设备错误修正技术[19]。这些研究方法在各自领域中对故障状态的研究都较为有效，但缺乏系统层面的研究方法和策略。就上述问题而言，参与者的目标是获得收益，针对事件故障状态而言即是安全收益。参与者存在安全和不安全行为策略，同时事件故障状态至少存在四种形式，且行为策略的实施也要考虑安全投入成本、安全效益分配等因素。因此上述这些方法都难以在这种条件下对参与者收益进行分析。

针对上述情况，作者提出使用量子态表示事件故障状态，使用博弈论研究参与者行为策略对事件故障状态的影响，在SFT理论框架[20]内研究参与者安全收益。同时借助SFT的方法提出了一些分析影响收益因素重要性的方法。研究认为多因素影响下的量子博弈参与者收益分析可应用SFT中方法，也完全可能使用因素空间理论进行研究。

1 事件故障状态与量子博弈

系统故障演化过程(System fault evolution process，SFEP)[21,22]是作者提出的描述系统故障发展过程中各事件、逻辑关系及影响因素的相互作用关系。空间故障网络理论(Space Fault Network，SFN)[23～25]用于描述和研究SFEP。SFEP中最重要的是事件、逻辑和因素，对应的SFN是节点及有向线段。SFEP的发生源于边缘事件的发生，经过过程事件的传递最终达到故障的结果，即最终事件。因此研究SFEP中的事件，特别是边缘事件的故障发生特点是关键。

进一步地，将边缘事件的故障特点简称为事件故障状态，进而研究单一事件故障状态。对事件故障总有对立合作的两方存在，一是管理者G，二是操作者C。G一般拥有系统，目的是保证系统运行，从而得到收益，同时监督C安全完成事件。C一般被G雇佣，目的是完成事件从而获得收益，希望减少自身行为的投入成本。G和C可采取安全行为Sa和不安全行为Us。G的Sa是根据规章制度履行职责，对C进行监督；G的是不充分履行或不履行对C的监督检查。C的是无论是否G检查，仍然按照规章制度安全完成事件；C的Us是只为完成事件，考虑降低安全行为甚至不采取安全行为完成事件。很显然G和C采取Sa的成本必将高于采取Ua的成本，但很难确定采取Sa就比Us获得更多的安全收益，因此双方都存在侥幸心理。这构成了以事件故障状态为对象，参与者收益目标，G和C采取不同行为获得不同收益的博弈过程。

给出基本参数，C：操作者；G：管理者；Sa安全行为，用量子态|0>表示；Us不安全行为，用量子态|1>表示；AG、BG、CG和DG都是G实施不同行为，C实施对策，G获得的收益；AC、BC、CC和DC都是C实施不同行为，G实施对策，C获得的收益；S：安全产出价值，在安全的生产过程中的产出价值量，类比于总产值；β：安全收益分配系数，取值范围[0,1]，表明从安全产出价值S中获得的安全收益；Z：安全措施成本，表明实施安全行为所需的成本。需要说明的事，由于目标是事件的安全性，即事件安全收益，因此如下确定的参与者收益是期望安全收益，在不引起歧义时统称为参与者收益。

现有博弈研究主要围绕参与者及其行为展开，进而得到参与者收益[6～8,10]，但缺少在安全和系统故障方面的类似研究。文中事件故障状态的研究不但需要考虑参与者G和C，及行为Sa和Us，还需考虑安全产出价值S、安全收益分配系数β、安全措施成本Z。参考类似的博弈研究[26～28]可得到事件故障状态的量子博弈收益矩阵，如表1所示。

表1 事件故障状态的量子博弈收益矩阵

表1可知双方都有两种行为可以实施。双方都采取Sa后双方收益为(1-β)S-ZG+βS-ZC=S-ZC-ZG。可见无论是双方总收益或是AG和AC都有可能大于0，这是最理想情况。当双方都采取Us时，即双方都采取不安全行为很可能导致事件无法完成，甚至出现损失(这里不考虑)。当一方采取Sa，但另一方采取Us时，当事件能完成时，采取Us的一方获得更大收益，Sa一方收益不变；当事件未完成时，采取Us的一方损失更小，Sa一方损失不变。这说明无论结果如何采用Us的一方更有优势。关于损失可折合成安全措施成本以ZG和ZC的形式呈现。

2 纠缠与非纠缠态的参与者收益

表1中四种参与者博弈状态可分别使用量子态|00>、|01>、|10>、|11>表示。结合文献[26,27]对类似问题的研究，给出如下参与者收益推导过程。

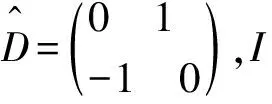
其中:θC,θG∈[0,π],φC,φG∈[0,π/2]。

参与者G和C执行Sa和Us的行为概率分别为:P00=|<00|ψ1>|2，P01=|<1|ψ1>|2，P10=|<10|ψ1>|2，P11=|<11|ψ1>|2。G的行为收益IG如式(4)所示。C的行为收益IC如式(5)所示。

3 参与者收益特征分析

由式(4)～(7)所示，当考虑纠缠态时，G的收益函数为IG=IG(β,φG,φC,γ,θG,θC)，C收益IG=IG(β,φG,φC,γ,θG,θC)；考虑非纠缠态时，G的收益函数为IG=IG(β,φG,φC,γ,θG,θC)，C收益IG=IG(β,φG,φC,γ,θG,θC)。当然他们也与S、ZG、ZC相关，但这些因素是在确定参与者收益之前设定的，不参与收益变化和特征分析。

进一步，借助SFT的多因素分析方法可对参与者收益与因素关系的特征进行分析。由于四个收益函数结构类似，这里以G的收益函数IG=IG(β,φG,φC,γ,θG,θC)为例进行说明，给出计算方法。但由于多维函数难以使用直观图像表示，这里不给出函数变化图像。将β,φG,φC,γ,θG,θC定义为影响IG的因素，那么β,φG,φC,γ,θG,θC与IG组成7维空间。这些因素同时变化的叠加形成空间分布曲面，如下所有定义均基于该曲面进行分析。

事件故障状态及其分析方法是多样的，上述研究主要是结合SFT和量子博弈进行的。量子态表示事件故障状态的多样性，博弈表示G和C以收益为目标的行为策略。最终得到了在β,φG,φC,γ,θG,θC因素影响下的参与者收益函数，并使用SFT理论的一些方法对其进行了研究。SFT主要分析影响因素与目标之间的关系，对多因素影响下的参与者收益分析特别适用。更多方法请参见作者相关论著，可广泛扩展基于量子博弈的参与者收益研究方法。

4 实例分析

根据前述的各变量定义，设定安全收益分配系数β=0.6，安全产出价值S=50，针对量子状态θC,θG=π/2(θC,θG∈[0,π]),φC,φG=π/4(φC,φG[0,π/2])，管理者实施安全措施的成本ZG=0.5，操作者实施安全措施的成本ZC=1.1；ZG和ZC的确定与安全产出价值S有关，S可理解为安全生产后的产出，ZG和ZC则是相应的管理者和操作者实施安全措施的成本；γ分别取0(非纠缠)，π/4(中间值)和π/2(最大值)。由式(4)和式(5)，带入上述参数可得式(8)。

当γ=0时，即非纠缠状态时，IG=6.0,IC=5.7,γ=π/4,IG=2.9375,IC=2.7125；当γ=π/2时，；当γ=π/2时，即最大纠缠时，IG=-0.125,IC=-0.275。从结果中可知，非纠缠时参与者双方都不考虑对方实施的行为情况，以自己中心实施行为，这时各自的收益应是最大的。而当参与者双方完全考虑对方采取的行为，而非根据实际情况确定行为时，实施行为的成本将增加和效益降低，这时两者的收益是负值。而在上述两种情况之间时，同时考虑对方行为和己方实际情况时将出现系统整体的收益最大值，即IG+IC的最大值。上述过程在趋势上是合理的，过程中的具体值还与β、S、θC、θG、φC、φG、ZG和ZC的值相关。

对因素重要度而言，例如考察γ对IG和IC的重要度，即为γ的变化造成IG和IC变化的程度，因此根据因素重要度定义，可将式(8)改写为式(9)。并通过式(9)得到参与者收益与纠缠程度的关系。

进一步讨论，在量子博弈中的参与者收益是目标函数，β,φG,φC,γ,θG,θC是影响因素，上述研究是在SFT框架下完成的。从另一角度，参与者收益是目标因素，β,φG,φC,γ,θG,θC是影响因素，这些因素组成了因素空间[30～32]，它们之间的关系组成了背景集。因此该问题也可在因素空间理论中进行讨论。因素空间理论被誉为智能科学的数学基础，主要研究因素间逻辑关系和推理。这为该问题的智能化处理奠定了基础，理论上因素空间的所有方法都可应用于该问题，相关论证将在后继研究中呈现。

5 结论

论文研究了事件故障状态量子博弈的参与者收益问题，具体结论如下：

1)研究了事件故障状态与量子博弈的关系。影响关系的因素包括管理者和操作者采取安全和不安全行为对量子博弈的影响，以及安全产出价值、安全收益分配系数、安全措施成本对收益函数的影响。讨论了参与者双方采取不同行为收益的变化情况。

2)研究了纠缠与非纠缠态的参与者收益。纠缠表示管理者和操作者之间存在信息联系。研究了初始状态为安全状态下的博弈过程。确定了管理者和操作者在纠缠和非纠缠态的收益函数，这些函数受到因素β,φG,φC,γ,θG,θC的影响。

3)研究了参与者收益受到各因素影响的特征。使用SFT的方法进行研究，提出了针对收益的因素重要度、因素联合重要度、收益风险区和安全区、因素区域重要度。理论上SFT的思想和方法都可用于量子博弈参与者收益问题的分析。进一步也论述了使用因素空间理论解决问题的可能性。