基于Hermite插值的管片拼装机轨迹规划

2023-02-28吕志斌秦东晨朱强陈江义

机床与液压 2023年3期

吕志斌，秦东晨，朱强，陈江义

(郑州大学机械与动力工程学院，河南郑州 450001)

0 前言

近几年，随着国内区域经济一体化的不断发展，轨道交通建设越来越热火朝天。同时，各大城市不断加大对地下空间的开发利用，使对周边环境影响小、施工速度快、工程质量优良、施工安全环保、适用范围广的盾构施工法越来越受到欢迎[1]，为盾构机打开了一个空前繁荣的市场。近年来,盾构机的国产化取得了长足的进展,国内多家单位都能完成盾构机的独立设计及制造[2]。管片拼装机是盾构机的重要组成部分，在管片拼装过程中，盾构停止掘进，主机处于静止状态[3]。在盾构向前掘进一环后，按预定要求将混凝土管片拼装成环，形成衬砌，以此来支护刚开挖的隧道表面[4]。其拼装质量、精度及效率直接影响隧道施工安全和进程[5]。

目前，KOSUGE等[6]进行了面向任务的盾构管片拼装力控系统的研究；程永龙等[7]提出了微型盾构半自动拼装技术；刘飞香[8]研究了智能化抓取以及智能化拼装方法；王明斗等[9]对矩形盾构的串联式管片拼装机进行了轨迹优化。另外隧道股份上海隧道工程有限公司研发了中国首台推拼同步盾构机[10]；李杰等人[11]对管片拼装机提升系统同步性能进行了研究。综合来看，这些学者在管片拼装机的液压仿真以及微调机构等方面做出了大量工作，但是对其进行轨迹优化的研究较少。王明斗等采用的是B样条曲线，它在两点间最高只能构造二阶函数。文中的研究对象是成都11号线盾构机的管片拼装机，为双提升臂拼装机。结合Hermite插值算法对其进行时间最优的轨迹优化，提出一种新的拼装轨迹规划方法，可以在条件较少的情况下构造高阶函数，使轨迹平滑，从而在降低启动冲击的同时，提升管片拼装机的拼装效率。

1 双提升臂拼装机

双提升臂拼装机的粗调机构是由平移系统、回转系统和提升系统三部分组成。回转系统搭载在平移系统之上，随平移系统一起运动；提升系统搭载在回转系统之上，从而实现平移和回转。其中平移系统和提升系统由对称的双液压缸来驱动；回转系统由对称的双液压马达驱动，在保证驱动力的同时，确保其精确度。管片拼装机的三维模型如图1所示。管片拼装时，平移系统控制水平位移，回转系统控制回转角度，提升系统控制管片高度。通过粗调机构到达指定位置附近，再由微调机构调整管片位姿偏差，完成管片拼装。

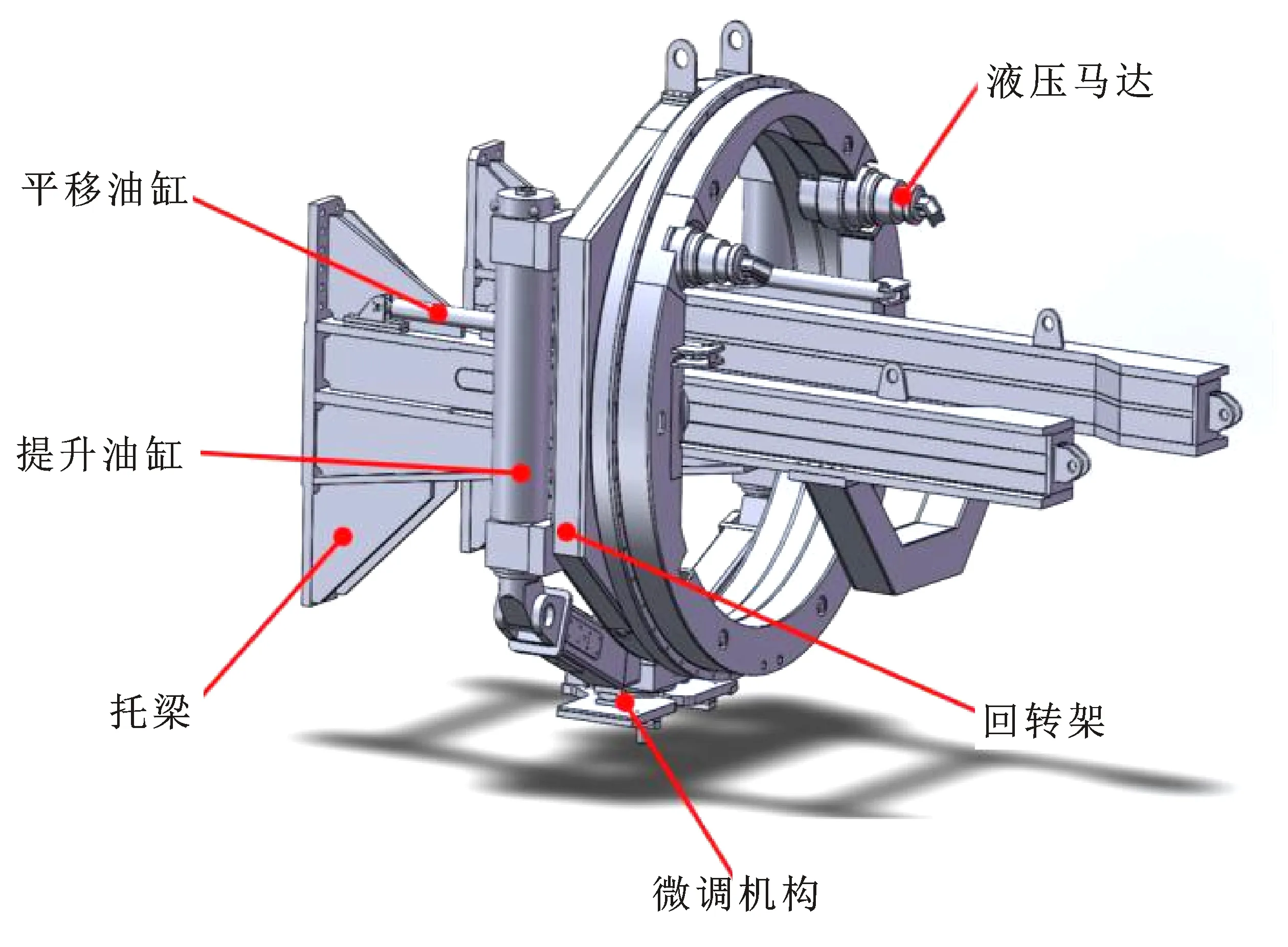
图1 管片拼装机三维模型Fig.1 Three dimensional model of segment assembler

由于对接机器视觉，其输出参数为直角坐标系下的三维向量(X,Y,Z)，而管片拼装机的输入参数为(l,θ,d)。其中：l为平移系统的位移，θ为回转系统的回转角度，d为提升系统的位移。因此需要求管片拼装机运动学方程的逆解。根据管片拼装机的结果易得其运动学方程为

(1)

式中：r1为机械结构在径向上的偏移距离；r2为机械结构在轴向上的偏移距离。

因此其运动学方程的逆解为

(2)

2 轨迹规划方法

由于管片质量达到了4 t，因此其空载和负载的受力有很大不同，空载时可以提高管片拼装机运行速度，负载时降低其运行速度，故将管片拼装的动作分为抓取、递送、安装以及回原点4个部分，从而充分发挥各阶段的特点，优化各阶段的轨迹，并且消除累计误差对管片拼装机自动拼装的影响。

2.1 轨迹规划方案

在始末速度优化中常用的方法为摆线轮廓速度法[12]，但是通过计算发现采用Hermite插值法将进一步降低冲击力。以启动时间1 s、最大速度1 m/s为例，对比两者的速度和加速度曲线如图2所示。

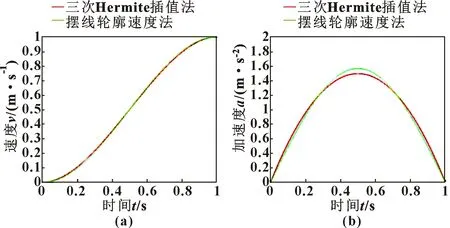
图2 两者速度(a)和加速度(b)对比

通过对比摆线轮廓速度法，发现在相同时间内提升到相同的速度三次Hermite插值法的加速度较小，减小了4.5%左右。也就是说在负载的情况下，启动冲击力减小了2 kN左右。

因此本文作者选用Hermite插值法对管片拼装机进行轨迹规划，其流程如图3所示。

图3 轨迹规划流程Fig.3 Trajectory planning flow chart

为了提高管片拼装效率，本文作者在保证加速度安全的前提下，采用三次Hermite插值算法将其速度平稳而快速地提升。由于每个动作都是由管片拼装机的平移、回转以及提升系统共同作业完成的，因此可以将其分解为3条速度-时间曲线。首先基于最大加速度的限制比较出各自的最快完成时间，选取用时最长的作为时间基准，其他两个动作基于这个时间基准和已知的位移量。为了保证拼装机高效率和平稳的运行，其运动轨迹曲线一般需要具有C2连续性[13]，因此采用五次Hermite插值算法规划出路径，从而使其在达到最优速度的前提下进一步降低其加速度。

2.2 加速度计算

将已知条件列表1如下。

表1 已知参数Tab.1 Known parameters

对于平移系统，只需考虑推力。

由F=ma可得，负载工况下

(3)

空载工况下

(4)

但是由于管片拼装机的额定功率为55 kW，经过计算在抓取阶段实际功率超出额定功率。经调整，空载工况下的加速度也改为4.17 m/s2。

对于回转系统，为了保证所求的角加速度在整个运动过程中都能达到，必须考虑其极限工况。即当回转角度为±90°时，重力扭矩最大，总扭矩最小。由T=Jα可得，负载工况下

(5)

空载工况下

(6)

其中：T1为管片重力产生的扭矩；T2为提升系统自重产生的扭矩；J1为管片绕回转中心的转动惯量；J2为提升系统绕回转中心的转动惯量；J3为回转系统绕回转中心的转动惯量。

经过计算在回原点阶段实际功率超出额定功率。经调整，空载工况下的加速度改为2.8 rad/s2。

对于提升系统，只需考虑提升力与重力。

由F=ma可得，负载工况下

12.84 m/s2

(7)

空载工况下

(8)

由于提升系统用时不长，通常不作为基准，不会满负荷运转，因此加速度不做调整。

2.3 轨迹规划方法

为了降低起停冲击，提高管片拼装机的运行平稳性，将起始位置和末尾位置的速度以及加速度设为零。

在平移过程中，假设其运行时间为t1，最高速度为v1，先用三次Hermite插值法表达出速度与时间的表达式

(9)

同理，回转和提升的表达式分别为

(10)

(11)

然后根据算出的最大加速度和输入的位移量，分别对多项式进行求导和积分，解出时间t和速度v。

通过对比三者的时间，选取时间最长的为基准动作，可得出该动作速度与时间的曲线。对多项式进行求导和积分，可得到加速度与时间的曲线以及位移与时间的曲线。

对于其他两个动作，根据已知的位移量和时间基准t，采用五次Hermite插值算法分别对位移进行分析，可计算出其余两个动作位移与时间的曲线，求导可得到速度与时间的曲线以及加速度与时间的曲线。

3 计算结果

通过管片拼装机的设计图纸，确定了各个动作的平移量、回转角度和提升量。其中液压缸伸出为正，缩回为负；顺时针回转为正，逆时针回转为负。

以K管片为例[14]，其中递送时需注意，当提升系统快达到管片厚度时，平移系统和回转系统均要到达指定位置，以防碰到已装好的管片。粗调参数列于表2中。

表2 K管片粗调参数Tab.2 K segment rough adjustment parameters

运用MATLAB算法得出管片拼装机的Hermite插值函数，将其导入ADAMS进行运动学仿真，绘制出K管片整体动作管片的位移、速度以及加速度的曲线如图4所示。

图4 运动学曲线

从图4中可以看出：在K管片拼装过程中，管片拼装机运行平稳。拼装分速度最大出现在回原点阶段的Y轴方向，约为2.7 m/s；合速度最大出现在回原点阶段，约为2.7 m/s。加速度曲线连续且无突变，能够使运动平稳，从而显著降低了系统冲击。其最大分加速度出现在回原点阶段X轴方向，约为5 m/s2。最大合加速度出现在回原点阶段，约为5 m/s2。

通过已知数据计算出各动作的大致运行时间，列于表3中。

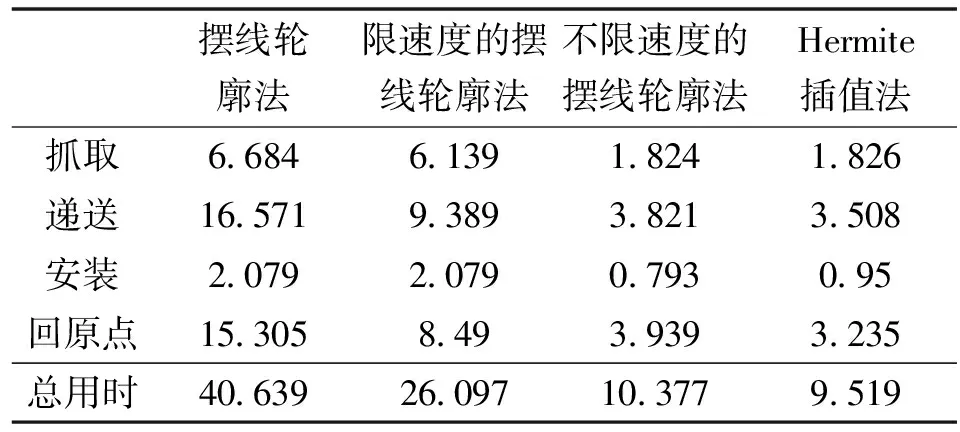
表3 运动时间单位：s

由表3可以看到，目前常用的摆线轮廓法作业各个系统在运行期间的总用时大致为40.639 s；即使采用3个系统并行运行，其总用时大致也要26.097 s；不限速度后的总用时大致为10.377 s。而采用文中的方法其总用时大致为9.519 s。相比于现在遥控拼装常用的摆线轮廓法作业，总用时降低了30.82 s，约75.8%；就算采用并行运行，总用时也降低了16.278 s，约62.4%。相比于不限速度的摆线轮廓法，总用时降低了0.858 s，约8.3%。因此文中采用的五次Hermite插值法拼装效率最高。

由于大多学者没有对此进行深入研究，因此没有过多的数据对比。且由于管片拼装机的微调整和后续环节主观性太大，无法用具体数据进行精确分析，文中做了相应的简化，仅做了管片拼装机粗调整的轨迹规划，但也大大提升了管片拼装机的拼装效率。