基于NMPC-PID的大型风力机独立变桨控制
2023-02-28周嘉玉郝万君
周嘉玉,郝万君
(苏州科技大学电子与信息工程学院,江苏苏州 215009)
0 前言
在风机桨叶旋转过程中,以恒定桨距角施加在旋转叶片上的气动载荷将随着转子平面中的风速而变化,从而引起振动载荷。由于风轮扫风面内风速的不均匀分布会使大型风力机的风轮产生不均衡载荷,会给变桨轴承、轮毂、主轴、偏航轴承、塔架等关键部件造成很大疲劳载荷[1]。独立变桨控制(Individual Pitch Control,IPC)就是当风速高于额定风速时改变叶片的桨距角,以减轻引起疲劳的振荡载荷。
现代控制理论中的模型预测控制(Model Predictive Control,MPC)汲取了优化思想,并用在线不断进行的有限时域优化,即所谓滚动优化,取代了传统最优控制中一次性的全局优化,且在滚动的每一步以实时信息进行反馈矫正[2]。因此MPC避免了辨识最小化参数模型的困难,降低了在线优化复杂度的同时能够控制关于最优准则的受约束的多输入多输出非线性系统,而且其预测能力具有干扰抑制和平滑控制信号的更好的轨迹跟踪性能[3-5]。文献[6]提出了更为经济的NMPC(Nonlinear Model Predictive Control)方法用于最大限度地提高风力涡轮发电机的发电量,而没有考虑到大型风力机在高风速区的载荷平衡问题。文献[7]提出了将LiDar瞬时风速预测与MPC相结合的方法应用于风机的独立变桨控制,但未考虑到风机外界干扰与不确定性影响。文献[8]提出了一种较为完善的基于内模控制(Internal Model Control,IMC)的独立变桨控制策略,但实际上获得风力机的内部模型十分困难。文献[9]提出了不同类别的独立变桨控制的设计要点以及MPC设计框架,具有很高的研究价值。
综上,针对之前研究中没有考虑到塔架振动、风力机模型的不确定性等不足,本文作者提出了一种NMPC-PID的大型风力发电系统的独立变桨载荷控制方法。综合考虑了非线性模型预测控制处理多输入多输出系统的能力以及风机系统的强非线性,且用PID技术减小了塔架振动的影响。
1 风电系统模型
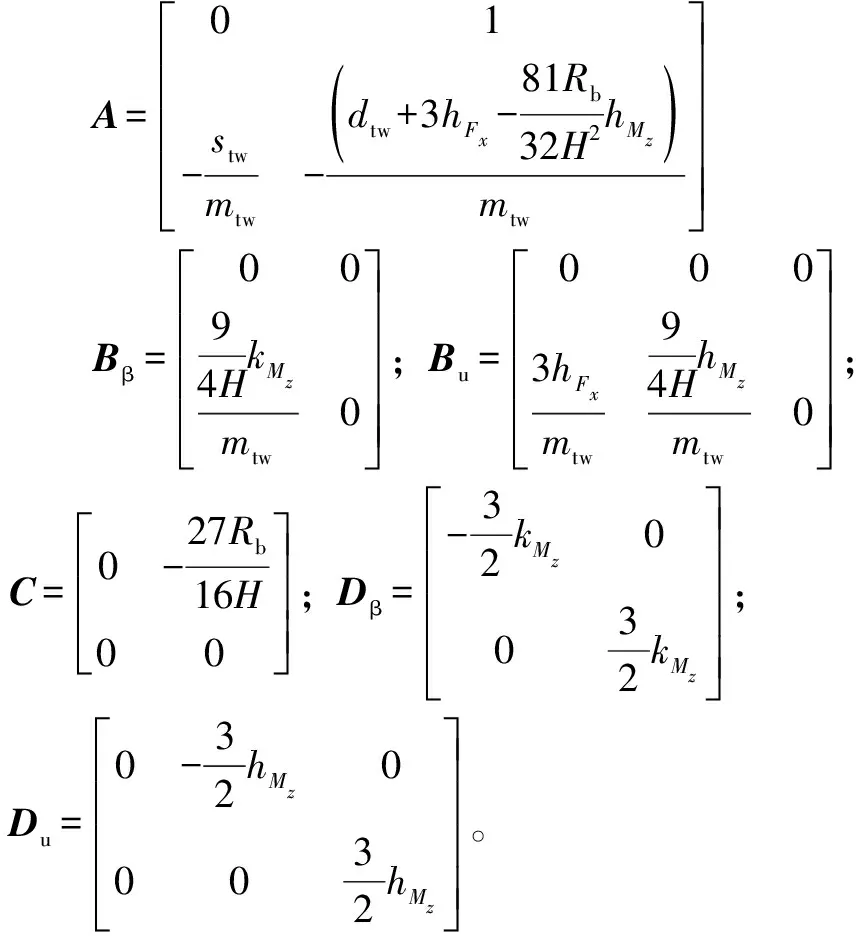
大型风力发电系统的空气动力学特性呈强非线性[10]。为了简化分析,可以将桨叶视为刚性叶片,并对载荷非线性模型在稳态工作点附近进行线性化,得到线性周期时变模型[11]。而Park变换实现风轮旋转坐标系转化为轮毂固定计算量,可将1P振荡转换成平均值,而其他振荡分量消失或转换为频率3P的倍数。简化的风力机模型[12]如下:
(1)
(2)
(3)
(4)

其中:Mzi、Fxi分别为第i个桨叶上叶片挥舞方向的力矩和力;Mxi、Fxi分别为第i个桨叶上叶片摆振方向的力矩和力;βi为第i个桨叶上的桨距角;vfli为第i个桨叶上叶片挥舞方向的相对有效风速,表示为
(5)
其中:ui为第i片桨叶上的等效风速;ψi为第i片桨叶的方位角。设第1片桨叶的方位角为ψ,那么
(6)

(7)
2 控制器设计
大型风力发电机组具有强非线性、模型不确定性的特点,很容易出现模型失配、工况点转移等问题。为此,本文作者提出基于NMPC-PID的控制策略,进行风电机组的载荷控制。
2.1 NMPC-IPC设计
NMPC使用风电系统的内部预测模型在线解决有限时域二次控制问题,并基于滚动时域原理仅实现最优输入序列的第一次控制移动。假设风力涡轮机系统动力学可以被认为是LTI(Linear Time Invariant)系统,下面的离散时间系统描述(具有采样间隔Ts)对应于(具有相同维度)增广系统。
(8)

约束条件为
(9)
其中:yk+i|k表示在采样时刻k预测在k+i时刻输出的值;参考信号rk+i(包括转子速度和叶片扇动弯矩的变化)设置为零,旨在最小化叶片疲劳并保持标称发电机功率输出;uk+j|k是控制输入序列;Np表示输出范围;Nc表示控制输入范围(通常Nc≤Np);Q和R是对称正定加权矩阵。约束条件表明了初始状态,以及说明了控制输入限值和相应的速率限值。传感器在每个采样时间测量风力涡轮机状态x0。
成本函数的矩阵公式可以表示为
(10)
其中:Q=CTQxC。由具有输入序列u(k)的线性状态空间模型(7)生成的预测状态序列可以表示为
xk+1=Mxk+cuk+εudk
(11)
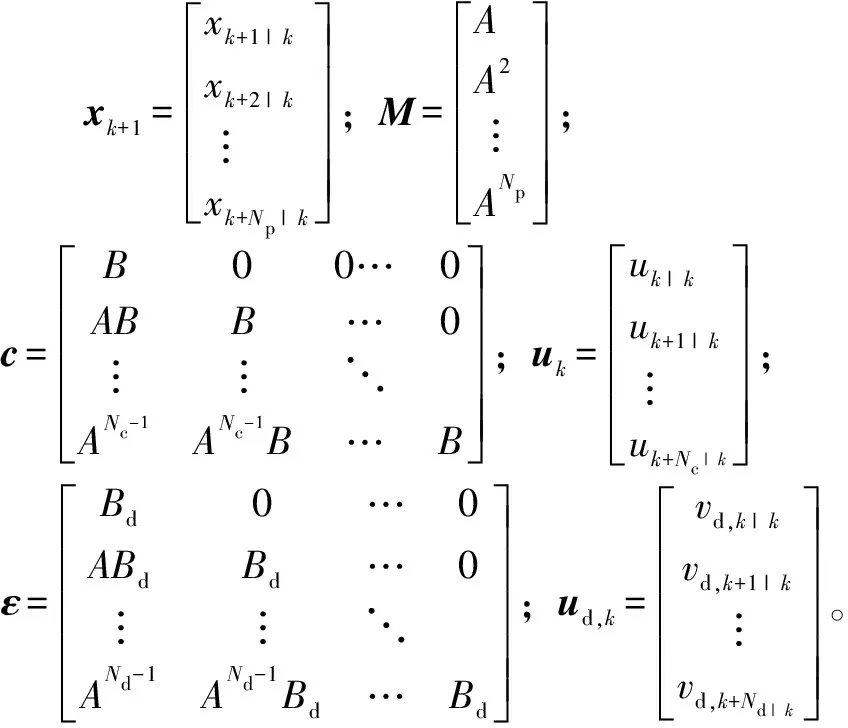
式中:xk+1表示在采样时刻k+1的预测状态向量;uk表示k和k+Nc采样间隔之间的最佳控制输入序列。预测的控制输入应该在控制范围Nc之外是恒定的。预测范围Nd内的有效风速视为扰动项ud,k。另外,Np应大于风速预测样本的范围(Np>Nc)。
结合式(8),可得:
(12)


2.2 塔架振动的抑制
对于纵向振动,当塔架逆风移动时,转子的相对风速小于塔架逆风移动时的相对风速。风速的这种差异导致转子速度信号中增加了周期性扰动信号。采用适当的桨距控制策略,减轻这种周期性扰动信号可以减少塔架振动。通过在转子速度信号中加入左右塔振动的影响,可以进一步降低塔振动。
为了实现内模控制,内模的状态空间形式与PID速度控制器并联,以抑制振动信号。关于振动信号的信息可以通过考虑内部模型的状态变量的运动轮廓来获得。
当转速高于额定风速时,PID变桨控制器限制转速。变量V表示高速风和电气机械扰动产生的振动信号,影响速度信号。x2是内模控制的输出信号,作为抵消项加到PID控制器的输出上。塔架振动抑制原理如图1所示。
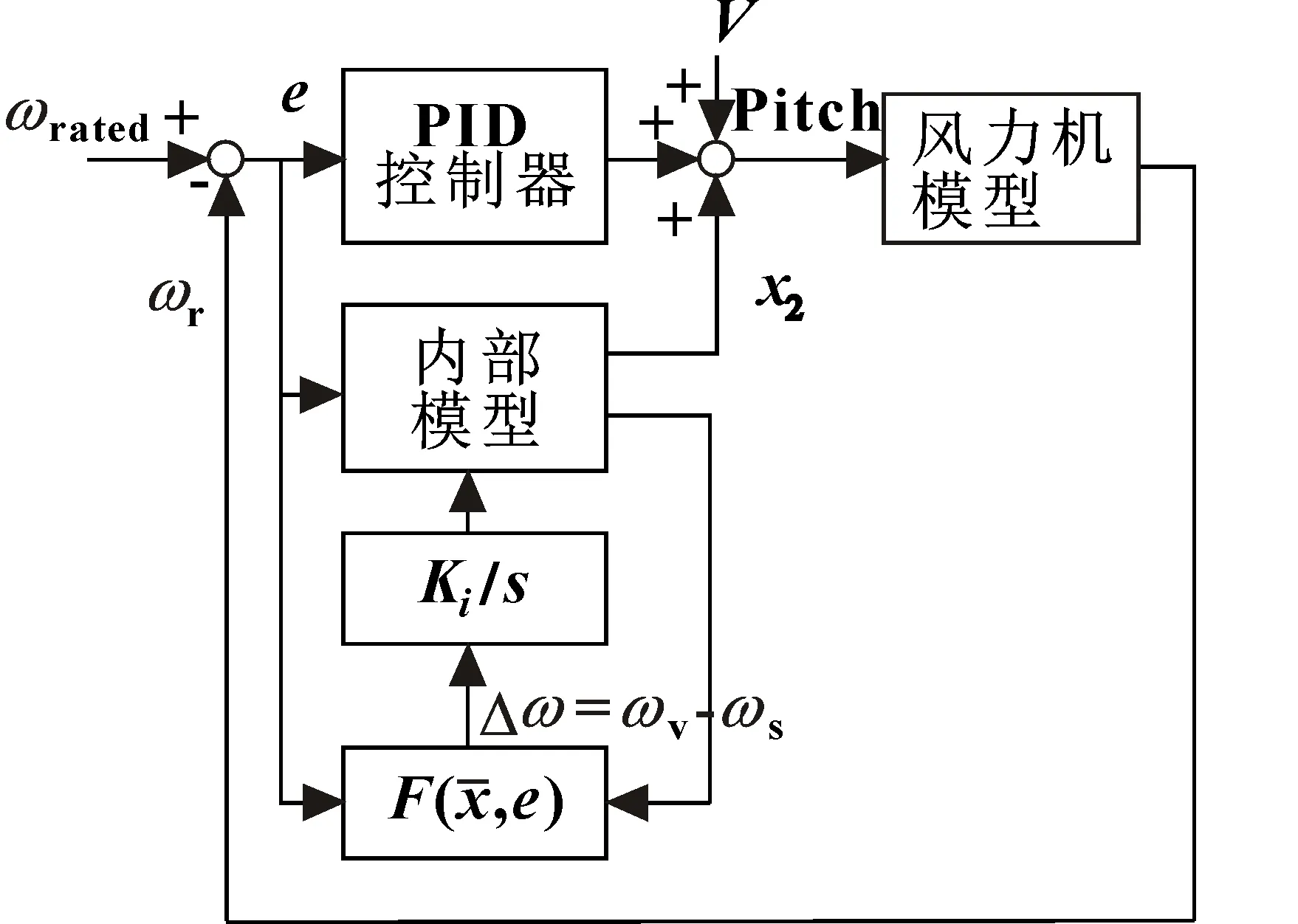
图1 塔架振动抑制原理Fig.1 Tower frame vibration suppression principle
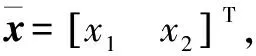
(13)

3 实验分析
所设计的风力机的独立变桨控制在MATLAB/Simulink仿真平台验证。在仿真平台搭建3 MW大型风力机模型,其基本参数设置见表1。

表1 风力机参数设置Tab.1 Wind turbine parameters setting
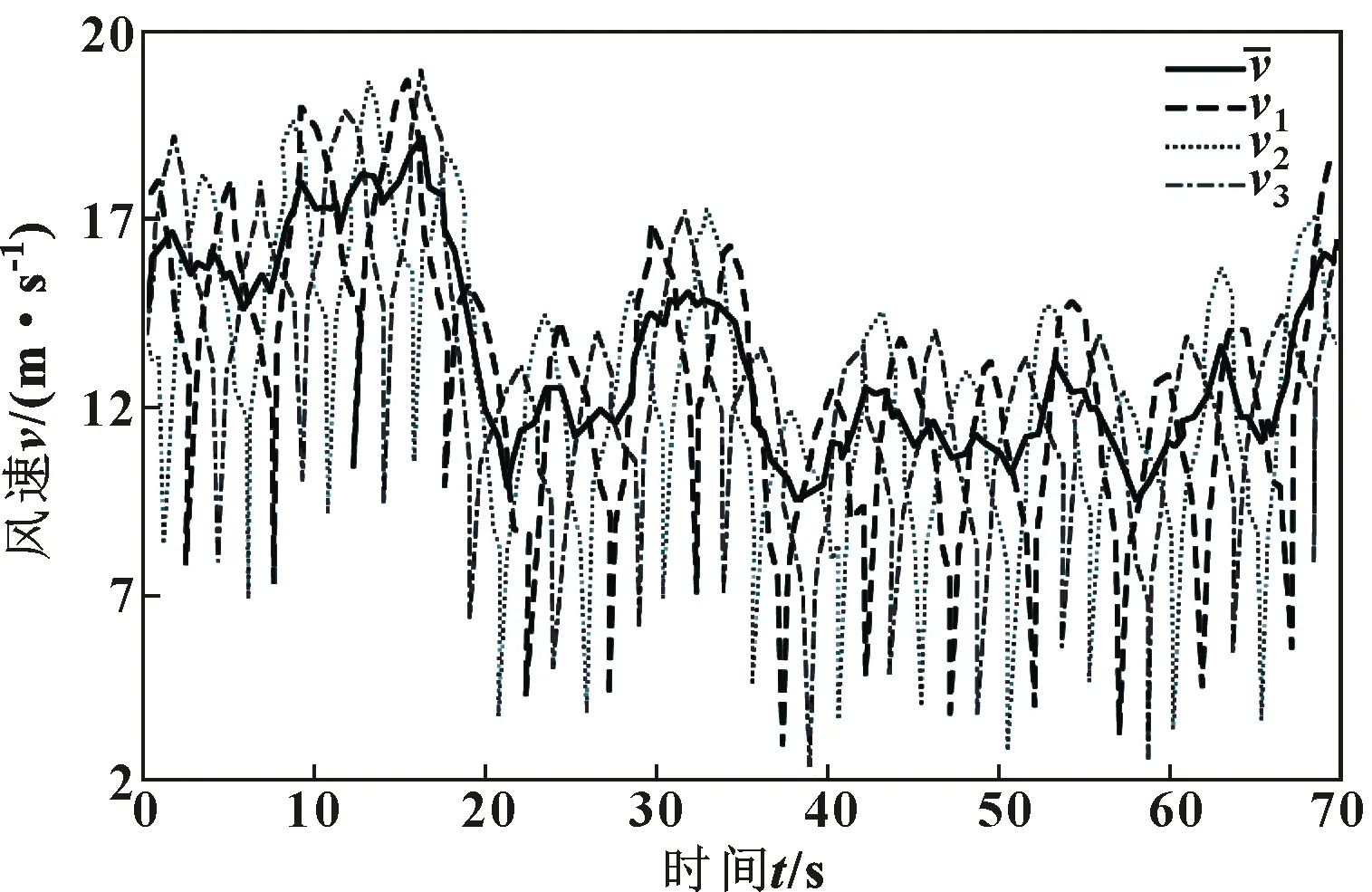
图2 风速曲线Fig.2 Wind speed profile
为了验证所提控制策略的有效性和可行性,分别在模型失配和有外界干扰的情况下进行仿真实验,对比文中所提策略与MPC的控制效果。图3为模型失配情况下的仿真结果,模型参数的变化范围为±10%,表2为两种控制方法的性能对比。

图3 模型失配下的力矩

表2 模型失配下的性能对比 单位:N·m
由图3看出:仿真前期,由于模型参数的变化,MPC的性能有所下降,因其依赖精确建模且只能针对典型的工况点,所以不能很好地控制风力机的载荷减小到期望值0;对比之下,NMPC-PID方法具有很好的鲁棒性,且考虑到了塔架振动的影响。从表2可以看出:文中所提NMPC-PID控制策略的俯仰力矩均值与标准差分别为-1.33×104N·m和7.16×104N·m,相较于MPC策略分别降低了38.14%和80.06%;NMPC-PID的偏航力矩的均值与标准差分别为-246.41 N·m和1.00×104N·m,相比较MPC策略分别降低了56.55%和67.75%。
图4为外界干扰下的仿真结果,通过加入高斯白噪声来模拟大型风力机的外界干扰,例如风剪切、塔影效应等。由图4可以看出:MPC方法没有很好的抗干扰能力,俯仰力矩与偏航力矩波动幅度较大;而NMPC-PID方法控制下的力矩均可在0附近小范围波动,因此其抗干扰能力与鲁棒性均优于MPC方法。从表3可以看出:文中所提NMPC-PID控制策略的俯仰力矩均值与标准差分别为-2.13×104N·m和1.16×105N·m,相较于MPC策略分别降低了59.35%和55.21%;NMPC-PID的偏航力矩的均值与标准差分别为6.41×102N·m和1.00×104N·m,相比较MPC策略分别降低了55.79%和75.73%。
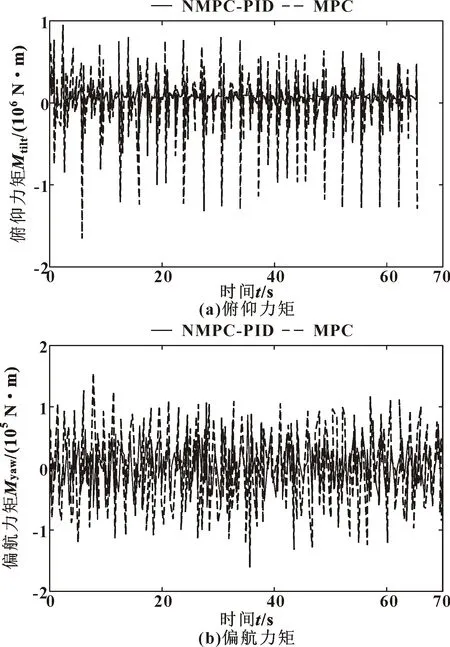
图4 外界干扰下的力矩

表3 外界扰动下的性能对比 单位:N·m
4 总结
针对大型风力发电机组在高风速区的不平衡载荷问题,提出一种NMPC-PID方法,并且在MATLAB/ Simulink平台搭建了风力机模型,进行了模型失配和外界干扰下的仿真实验。
(1)在实验中,通过对比得出NMPC-PID方法有效提高了控制器的性能,减轻了塔架振动的影响,具有一定的创新性;
(2)仿真实验的实验条件与对比实验均有局限,未来的研究工作将围绕着更加复杂的实验条件,例如湍流风等,以及其他预测控制方法用于实验;
(3)文中只是在仿真平台做了仿真实验,实际系统具有更强的不确定性和未建模动态,所以文中所提方法真正用在工程上还有很长的路要走。
